Le funzioni elementari di base, le loro proprietà intrinseche ei grafici corrispondenti sono una delle basi della conoscenza matematica, simile per importanza alla tabellina. Le funzioni elementari sono la base, il supporto per lo studio di tutte le questioni teoriche.

L'articolo seguente fornisce materiale chiave sull'argomento delle funzioni elementari di base. Introdurremo termini, daremo loro definizioni; Studiamo in dettaglio ogni tipo di funzione elementare e analizziamo le loro proprietà.

Si distinguono i seguenti tipi di funzioni elementari di base:

Definizione 1

• funzione costante (costante);
• radice dell'ennesimo grado;
• funzione di alimentazione;
• funzione esponenziale;
• funzione logaritmica;
• funzioni trigonometriche;
• funzioni trigonometriche fraterne.

Una funzione costante è definita dalla formula: y = C (C è un numero reale) e ha anche un nome: costante. Questa funzione determina se un qualsiasi valore reale della variabile indipendente x corrisponde allo stesso valore della variabile y – il valore C .

Il grafico di una costante è una linea retta parallela all'asse x e passante per un punto avente coordinate (0, C). Per chiarezza, presentiamo grafici di funzioni costanti y = 5 , y = - 2 , y = 3 , y = 3 (contrassegnate rispettivamente in nero, rosso e blu nel disegno).

Definizione 2

Questa funzione elementare è definita dalla formula y = x n (n - numero naturale più di una).

Consideriamo due varianti della funzione.

1. Radice dell'ennesimo grado, n è un numero pari

Per chiarezza indichiamo il disegno, che mostra i grafici di tali funzioni: y = x , y = x 4 e y = x 8 . Queste funzioni sono codificate a colori: rispettivamente nero, rosso e blu.

Una vista simile dei grafici della funzione di un grado pari per altri valori dell'indicatore.

Definizione 3

Proprietà della radice della funzione dell'ennesimo grado, n è un numero pari

• il dominio di definizione è l'insieme di tutti i non negativi numeri reali [ 0 , + ∞) ;
• quando x = 0 , la funzione y = x n ha valore uguale a zero;
• dato funzione - funzione vista generale(non è né pari né dispari);
• intervallo: [ 0 , + ∞) ;
• questa funzione y = x n con esponenti pari della radice aumenta sull'intero dominio di definizione;
• la funzione ha una convessità con direzione ascendente sull'intero dominio di definizione;
• non ci sono punti di flesso;
• non ci sono asintoti;
• il grafico della funzione per n pari passa per i punti (0 ; 0) e (1 ; 1) .

1. Radice dell'ennesimo grado, n è un numero dispari

Tale funzione è definita sull'intero insieme dei numeri reali. Per chiarezza, considera i grafici delle funzioni y = x 3 , y = x 5 e x9. Nel disegno sono indicati dai colori: rispettivamente nero, rosso e blu delle curve.

Altri valori dispari dell'esponente della radice della funzione y = x n daranno un grafico di forma simile.

Definizione 4

Proprietà della radice della funzione dell'ennesimo grado, n è un numero dispari

• il dominio di definizione è l'insieme di tutti i numeri reali;
• questa funzione è dispari;
• l'intervallo di valori è l'insieme di tutti i numeri reali;
• la funzione y = x n con esponenti dispari della radice aumenta sull'intero dominio di definizione;
• la funzione ha concavità sull'intervallo (- ∞ ; 0 ] e convessità sull'intervallo [ 0 , + ∞) ;
• il punto di flesso ha coordinate (0 ; 0) ;
• non ci sono asintoti;
• il grafico della funzione per n dispari passa per i punti (- 1 ; - 1) , (0 ; 0) e (1 ; 1) .

Funzione di alimentazione

Definizione 5

La funzione di potenza è definita dalla formula y = x a .

Il tipo di grafici e le proprietà della funzione dipendono dal valore dell'esponente.

• quando una funzione di potenza ha un esponente intero a, allora la forma del grafico della funzione di potenza e le sue proprietà dipendono dal fatto che l'esponente sia pari o dispari, e anche dal segno che ha l'esponente. Consideriamo di seguito tutti questi casi speciali in modo più dettagliato;
• l'esponente può essere frazionario o irrazionale - a seconda di ciò, variano anche il tipo di grafici e le proprietà della funzione. Analizzeremo casi speciali impostando diverse condizioni: 0< a < 1 ; a > 1 ; - 1 < a < 0 и a < - 1 ;
• una funzione di potenza può avere un esponente zero, analizzeremo anche questo caso in modo più dettagliato di seguito.

Analizziamo la funzione di potenza y = x a quando a è dispari numero positivo, ad esempio, a = 1 , 3 , 5 ...

Per chiarezza indichiamo i grafici di tali funzioni di potenza: y = x (colore nero del grafico), y = x 3 (colore blu del grafico), y = x 5 (colore rosso del grafico), y = x 7 (grafico verde). Quando a = 1 , otteniamo una funzione lineare y = x .

Definizione 6

Proprietà di una funzione di potenza quando l'esponente è un positivo dispari

• la funzione è crescente per x ∈ (- ∞ ; + ∞) ;
• la funzione è convessa per x ∈ (- ∞ ; 0 ] e concava per x ∈ [ 0 ; + ∞) (esclusa la funzione lineare);
• il punto di flesso ha coordinate (0 ; 0) (esclusa la funzione lineare);
• non ci sono asintoti;
• punti di passaggio della funzione: (- 1 ; - 1) , (0 ; 0) , (1 ; 1) .

Analizziamo la funzione di potenza y = x a quando a è un numero positivo pari, ad esempio a = 2 , 4 , 6 ...

Per chiarezza indichiamo i grafici di tali funzioni di potenza: y \u003d x 2 (colore nero del grafico), y = x 4 (colore blu del grafico), y = x 8 (colore rosso del grafico). Quando a = 2, otteniamo una funzione quadratica il cui grafico è una parabola quadratica.

Definizione 7

Proprietà di una funzione di potenza quando l'esponente è anche positivo:

• dominio di definizione: x ∈ (- ∞ ; + ∞) ;
• decrescente per x ∈ (- ∞ ; 0 ] ;
• la funzione è concava per x ∈ (- ∞ ; + ∞) ;
• non ci sono punti di flesso;
• non ci sono asintoti;
• punti di passaggio della funzione: (- 1 ; 1) , (0 ; 0) , (1 ; 1) .

La figura seguente mostra esempi di grafici di funzioni esponenziali y = x a quando a è un numero negativo dispari: y = x - 9 (colore nero del grafico); y = x - 5 (colore blu del grafico); y = x - 3 (colore rosso del grafico); y = x - 1 (grafico verde). Quando a \u003d - 1, otteniamo una proporzionalità inversa, il cui grafico è un'iperbole.

Definizione 8

Proprietà della funzione di potenza quando l'esponente è dispari negativo:

Quando x \u003d 0, otteniamo una discontinuità del secondo tipo, poiché lim x → 0 - 0 x a \u003d - ∞, lim x → 0 + 0 x a \u003d + ∞ per a \u003d - 1, - 3, - 5, .... Pertanto, la retta x = 0 è un asintoto verticale;

• intervallo: y ∈ (- ∞ ; 0) ∪ (0 ; + ∞) ;
• la funzione è dispari perché y (- x) = - y (x) ;
• la funzione è decrescente per x ∈ - ∞ ; 0 ∪ (0 ; + ∞) ;
• la funzione è convessa per x ∈ (- ∞ ; 0) e concava per x ∈ (0 ; + ∞) ;
• non ci sono punti di flesso;

k = lim x → ∞ x a x = 0 , b = lim x → ∞ (x a - k x) = 0 ⇒ y = k x + b = 0 quando a = - 1 , - 3 , - 5 , . . . .

• punti di passaggio della funzione: (- 1 ; - 1) , (1 ; 1) .

La figura seguente mostra esempi di grafici delle funzioni di potenza y = x a quando a è un numero pari negativo: y = x - 8 (grafico in nero); y = x - 4 (colore blu del grafico); y = x - 2 (colore rosso del grafico).

Definizione 9

Proprietà della funzione di potenza quando l'esponente è anche negativo:

• dominio di definizione: x ∈ (- ∞ ; 0) ∪ (0 ; + ∞) ;

Quando x \u003d 0, otteniamo una discontinuità del secondo tipo, poiché lim x → 0 - 0 x a \u003d + ∞, lim x → 0 + 0 x a \u003d + ∞ per a \u003d - 2, - 4, - 6, .... Pertanto, la retta x = 0 è un asintoto verticale;

• la funzione è pari perché y (- x) = y (x) ;
• la funzione è crescente per x ∈ (- ∞ ; 0) e decrescente per x ∈ 0 ; +∞ ;
• la funzione è concava per x ∈ (- ∞ ; 0) ∪ (0 ; + ∞) ;
• non ci sono punti di flesso;
• l'asintoto orizzontale è una retta y = 0 perché:

k = lim x → ∞ x un x = 0 , b = lim x → ∞ (x a - k x) = 0 ⇒ y = k x + b = 0 quando a = - 2 , - 4 , - 6 , . . . .

• punti di passaggio della funzione: (- 1 ; 1) , (1 ; 1) .

Fin dall'inizio, prestare attenzione al seguente aspetto: nel caso in cui a sia una frazione positiva con denominatore dispari, alcuni autori prendono l'intervallo - ∞ come dominio di definizione di questa funzione di potenza; + ∞ , stabilendo che l'esponente a è una frazione irriducibile. Al momento, gli autori di molte pubblicazioni didattiche sull'algebra e gli inizi dell'analisi NON DEFINONO funzioni di potere, dove l'esponente è una frazione con denominatore dispari a valori negativi discussione. Inoltre, aderiremo proprio a tale posizione: prendiamo l'insieme [ 0 ; +∞) . Raccomandazione per gli studenti: scoprire a questo punto il punto di vista dell'insegnante per evitare disaccordi.

Quindi diamo un'occhiata alla funzione di alimentazione y = x a quando l'esponente è un numero razionale o irrazionale a condizione che 0< a < 1 .

Illustriamo con grafici le funzioni di potenza y = x a quando a = 11 12 (grafico in nero); a = 5 7 (colore rosso del grafico); a = 1 3 (colore blu del grafico); a = 2 5 (colore verde del grafico).

Altri valori dell'esponente a (supponendo 0< a < 1) дадут аналогичный вид графика.

Definizione 10

Proprietà della funzione di potenza a 0< a < 1:

• intervallo: y ∈ [ 0 ; +∞) ;
• la funzione è crescente per x ∈ [ 0 ; +∞) ;
• la funzione ha convessità per x ∈ (0 ; + ∞) ;
• non ci sono punti di flesso;
• non ci sono asintoti;

Analizziamo la funzione di potenza y = x a quando l'esponente è un numero razionale o irrazionale non intero a condizione che a > 1 .

Illustriamo i grafici della funzione di potenza y \u003d x a in determinate condizioni utilizzando le seguenti funzioni come esempio: y \u003d x 5 4, y \u003d x 4 3, y \u003d x 7 3, y \u003d x 3 π (nero, rosso, blu, verde rispettivamente grafici).

Altri valori dell'esponente a nella condizione a > 1 daranno una vista simile del grafico.

Definizione 11

Proprietà della funzione di potenza per a > 1:

• dominio di definizione: x ∈ [ 0 ; +∞) ;
• intervallo: y ∈ [ 0 ; +∞) ;
• questa funzione è una funzione di forma generale (non è né dispari né pari);
• la funzione è crescente per x ∈ [ 0 ; +∞) ;
• la funzione è concava per x ∈ (0 ; + ∞) (quando 1< a < 2) и выпуклость при x ∈ [ 0 ; + ∞) (когда a > 2);
• non ci sono punti di flesso;
• non ci sono asintoti;
• punti di passaggio della funzione: (0 ; 0) , (1 ; 1) .

Attiriamo la vostra attenzione Quando a è una frazione negativa con denominatore dispari, nei lavori di alcuni autori si ritiene che il dominio di definizione in questo caso sia l'intervallo - ∞; 0 ∪ (0 ; + ∞) con la condizione che l'esponente a sia una frazione irriducibile. Al momento gli autori materiale didattico secondo l'algebra e gli inizi dell'analisi, le funzioni di potenza con un esponente in forma di frazione con denominatore dispari con valori negativi dell'argomento NON sono DEFINITE. Inoltre, aderiamo proprio a questo punto di vista: prendiamo l'insieme (0 ; + ∞) come dominio delle funzioni di potenza con esponenti negativi frazionari. Suggerimento per gli studenti: chiarisci a questo punto la visione del tuo insegnante per evitare disaccordi.

Continuiamo l'argomento e analizziamo la funzione di potenza y = x a fornito: - 1< a < 0 .

Ecco un disegno di grafici caratteristiche successive: y = x - 5 6 , y = x - 2 3 , y = x - 1 2 2 , y = x - 1 7 (rispettivamente linee nere, rosse, blu e verdi).

Definizione 12

Proprietà della funzione di potenza a - 1< a < 0:

lim x → 0 + 0 x a = + ∞ quando - 1< a < 0 , т.е. х = 0 – вертикальная асимптота;

• intervallo: y ∈ 0 ; +∞ ;
• questa funzione è una funzione di forma generale (non è né dispari né pari);
• non ci sono punti di flesso;

Il disegno seguente mostra i grafici delle funzioni di potenza y = x - 5 4 , y = x - 5 3 , y = x - 6 , y = x - 24 7 (nero, rosso, blu, colori verdi rispettivamente le curve).

Definizione 13

Proprietà della funzione di potenza per a< - 1:

• dominio di definizione: x ∈ 0 ; +∞ ;

lim x → 0 + 0 x a = + ∞ quando a< - 1 , т.е. х = 0 – вертикальная асимптота;

• intervallo: y ∈ (0 ; + ∞) ;
• questa funzione è una funzione di forma generale (non è né dispari né pari);
• la funzione è decrescente per x ∈ 0; +∞ ;
• la funzione è concava per x ∈ 0; +∞ ;
• non ci sono punti di flesso;
• asintoto orizzontale - linea retta y = 0;
• punto di passaggio della funzione: (1 ; 1) .

Quando a \u003d 0 e x ≠ 0, otteniamo la funzione y \u003d x 0 \u003d 1, che determina la linea da cui è escluso il punto (0; 1) (abbiamo convenuto che l'espressione 0 0 non sarà data qualsiasi valore).

La funzione esponenziale ha la forma y = a x , dove a > 0 e a ≠ 1 , e il grafico di questa funzione appare diverso in base al valore della base a . Consideriamo casi speciali.

Consideriamo prima la situazione quando la base funzione esponenziale ha un valore da zero a uno (0< a < 1) . Un esempio illustrativo sono i grafici delle funzioni per a = 1 2 (colore blu della curva) e a = 5 6 (colore rosso della curva).

I grafici della funzione esponenziale avranno forma simile per altri valori della base, a patto che 0< a < 1 .

Definizione 14

Proprietà di una funzione esponenziale quando la base è minore di uno:

• intervallo: y ∈ (0 ; + ∞) ;
• questa funzione è una funzione di forma generale (non è né dispari né pari);
• una funzione esponenziale la cui base è minore di uno è decrescente sull'intero dominio di definizione;
• non ci sono punti di flesso;
• l'asintoto orizzontale è la retta y = 0 con la variabile x tendente a + ∞ ;

Consideriamo ora il caso in cui la base della funzione esponenziale è maggiore di uno (a > 1).

Illustriamo questo caso speciale con il grafico delle funzioni esponenziali y = 3 2 x (colore blu della curva) e y = e x (colore rosso del grafico).

Altri valori della base, maggiori di uno, daranno una vista simile del grafico della funzione esponenziale.

Definizione 15

Proprietà della funzione esponenziale quando la base è maggiore di uno:

• il dominio di definizione è l'intero insieme dei numeri reali;
• intervallo: y ∈ (0 ; + ∞) ;
• questa funzione è una funzione di forma generale (non è né dispari né pari);
• una funzione esponenziale la cui base è maggiore di uno è crescente per x ∈ - ∞ ; +∞ ;
• la funzione è concava per x ∈ - ∞ ; +∞ ;
• non ci sono punti di flesso;
• asintoto orizzontale - retta y = 0 con variabile x tendente a -∞;
• punto di passaggio della funzione: (0 ; 1) .

La funzione logaritmica ha la forma y = log a (x) , dove a > 0 , a ≠ 1 .

Tale funzione è definita solo per valori positivi dell'argomento: per x ∈ 0 ; +∞ .

Programma funzione logaritmica ha una forma diversa, in base al valore della base a.

Considera prima la situazione in cui 0< a < 1 . Продемонстрируем этот частный случай графиком логарифмической функции при a = 1 2 (синий цвет кривой) и а = 5 6 (красный цвет кривой).

Altri valori della base, non maggiori di uno, daranno una vista simile del grafico.

Definizione 16

Proprietà di una funzione logaritmica quando la base è minore di uno:

• dominio di definizione: x ∈ 0 ; +∞ . Poiché x tende a zero da destra, i valori della funzione tendono a + ∞;
• intervallo: y ∈ - ∞ ; +∞ ;
• questa funzione è una funzione di forma generale (non è né dispari né pari);
• logaritmico
• la funzione è concava per x ∈ 0; +∞ ;
• non ci sono punti di flesso;
• non ci sono asintoti;

Analizziamo ora un caso particolare in cui la base della funzione logaritmica è maggiore di uno: a > 1 . Nel disegno sottostante, ci sono i grafici delle funzioni logaritmiche y = log 3 2 x e y = ln x (rispettivamente i colori blu e rosso dei grafici).

Altri valori della base maggiori di uno daranno una vista simile del grafico.

Definizione 17

Proprietà di una funzione logaritmica quando la base è maggiore di uno:

• dominio di definizione: x ∈ 0 ; +∞ . Poiché x tende a zero da destra, i valori della funzione tendono a - ∞;
• intervallo: y ∈ - ∞ ; + ∞ (l'intero insieme dei numeri reali);
• questa funzione è una funzione di forma generale (non è né dispari né pari);
• la funzione logaritmica è crescente per x ∈ 0; +∞ ;
• la funzione ha convessità per x ∈ 0; +∞ ;
• non ci sono punti di flesso;
• non ci sono asintoti;
• punto di passaggio della funzione: (1 ; 0) .

Le funzioni trigonometriche sono seno, coseno, tangente e cotangente. Analizziamo le proprietà di ciascuno di essi e i grafici corrispondenti.

In generale, tutte le funzioni trigonometriche sono caratterizzate dalla proprietà della periodicità, cioè quando i valori della funzione vengono ripetuti a significati diversi argomento, che differiscono tra loro per il valore del periodo f (x + T) = f (x) (T è il periodo). Pertanto, l'elemento "periodo meno positivo" viene aggiunto all'elenco delle proprietà delle funzioni trigonometriche. Inoltre, indicheremo tali valori dell'argomento per cui la funzione corrispondente scompare.

1. Funzione seno: y = sin(x)

Il grafico di questa funzione è chiamato onda sinusoidale.

Definizione 18

Proprietà della funzione seno:

• dominio di definizione: l'intero insieme dei numeri reali x ∈ - ∞ ; +∞ ;
• la funzione svanisce quando x = π k , dove k ∈ Z (Z è l'insieme degli interi);
• la funzione è crescente per x ∈ - π 2 + 2 π · k ; π 2 + 2 π k , k ∈ Z e decrescente per x ∈ π 2 + 2 π k ; 3 π 2 + 2 π k , k ∈ Z ;
• la funzione seno ha massimi locali nei punti π 2 + 2 π · k ; 1 e minimi locali nei punti - π 2 + 2 π · k ; - 1 , k ∈ Z ;
• la funzione seno è concava quando x ∈ - π + 2 π k; 2 π k , k ∈ Z e convesso quando x ∈ 2 π k ; π + 2 π k , k ∈ Z ;
• non ci sono asintoti.

1. funzione coseno: y=cos(x)

Il grafico di questa funzione è chiamato onda coseno.

Definizione 19

Proprietà della funzione coseno:

• dominio di definizione: x ∈ - ∞ ; +∞ ;
• il periodo positivo più piccolo: T \u003d 2 π;
• intervallo: y ∈ - 1 ; uno ;
• questa funzione è pari, poiché y (- x) = y (x) ;
• la funzione è crescente per x ∈ - π + 2 π · k ; 2 π · k , k ∈ Z e decrescente per x ∈ 2 π · k ; π + 2 π k , k ∈ Z ;
• la funzione coseno ha massimi locali nei punti 2 π · k ; 1 , k ∈ Z e minimi locali nei punti π + 2 π · k ; - 1 , k ∈ z ;
• la funzione coseno è concava quando x ∈ π 2 + 2 π · k ; 3 π 2 + 2 π k , k ∈ Z e convesso quando x ∈ - π 2 + 2 π k ; π 2 + 2 π · k , k ∈ Z ;
• i punti di flesso hanno coordinate π 2 + π · k ; 0 , k ∈ Z
• non ci sono asintoti.

1. Funzione tangente: y = tg (x)

Viene chiamato il grafico di questa funzione tangenziale.

Definizione 20

Proprietà della funzione tangente:

• dominio di definizione: x ∈ - π 2 + π · k ; π 2 + π k , dove k ∈ Z (Z è l'insieme degli interi);
• Il comportamento della funzione tangente sul confine del dominio di definizione lim x → π 2 + π · k + 0 t g (x) = - ∞ , lim x → π 2 + π · k - 0 t g (x) = + ∞ . Pertanto, le linee x = π 2 + π · k k ∈ Z sono asintoti verticali;
• la funzione svanisce quando x = π k per k ∈ Z (Z è l'insieme degli interi);
• intervallo: y ∈ - ∞ ; +∞ ;
• questa funzione è dispari perché y (- x) = - y (x) ;
• la funzione è crescente a -π 2 + π · k ; π 2 + π k , k ∈ Z ;
• la funzione tangente è concava per x ∈ [ π · k ; π 2 + π k) , k ∈ Z e convesso per x ∈ (- π 2 + π k ; π k ] , k ∈ Z ;
• i punti di flesso hanno coordinate π k; 0 , k ∈ Z ;

1. Funzione cotangente: y = c t g (x)

Il grafico di questa funzione è chiamato cotangenteide. .

Definizione 21

Proprietà della funzione cotangente:

• dominio di definizione: x ∈ (π k ; π + π k) , dove k ∈ Z (Z è l'insieme degli interi);

Comportamento della funzione cotangente al confine del dominio di definizione lim x → π · k + 0 t g (x) = + ∞ , lim x → π · k - 0 t g (x) = - ∞ . Pertanto, le linee x = π k k ∈ Z sono asintoti verticali;

• il periodo positivo più piccolo: T \u003d π;
• la funzione svanisce quando x = π 2 + π k per k ∈ Z (Z è l'insieme degli interi);
• intervallo: y ∈ - ∞ ; +∞ ;
• questa funzione è dispari perché y (- x) = - y (x) ;
• la funzione è decrescente per x ∈ π · k ; π + π k , k ∈ Z ;
• la funzione cotangente è concava per x ∈ (π k ; π 2 + π k ] , k ∈ Z e convessa per x ∈ [ - π 2 + π k ; π k) , k ∈ Z ;
• i punti di flesso hanno coordinate π 2 + π · k ; 0 , k ∈ Z ;
• non ci sono asintoti obliqui e orizzontali.

Le funzioni trigonometriche inverse sono l'arcoseno, l'arcocoseno, l'arcotangente e l'arcocotangente. Spesso, a causa della presenza del prefisso "arco" nel nome, le funzioni trigonometriche inverse sono chiamate funzioni ad arco. .

1. Funzione arcoseno: y = a r c sin (x)

Definizione 22

Proprietà della funzione arcoseno:

• questa funzione è dispari perché y (- x) = - y (x) ;
• la funzione arcoseno è concava per x ∈ 0; 1 e convessità per x ∈ - 1 ; 0;
• i punti di flesso hanno coordinate (0 ; 0) , è anche lo zero della funzione;
• non ci sono asintoti.

1. Funzione arcoseno: y = a r c cos (x)

Definizione 23

Proprietà della funzione arcoseno:

• dominio di definizione: x ∈ - 1 ; uno ;
• intervallo: y ∈ 0 ; π;
• questa funzione è di forma generale (né pari né dispari);
• la funzione è decrescente sull'intero dominio di definizione;
• la funzione arcoseno è concava per x ∈ - 1 ; 0 e convessità per x ∈ 0 ; uno ;
• i punti di flesso hanno coordinate 0 ; π2;
• non ci sono asintoti.

1. Funzione arcotangente: y = a r c t g (x)

Definizione 24

Proprietà della funzione arcotangente:

• dominio di definizione: x ∈ - ∞ ; +∞ ;
• intervallo: y ∈ - π 2 ; π2;
• questa funzione è dispari perché y (- x) = - y (x) ;
• la funzione è crescente nell'intero dominio di definizione;
• la funzione arctangente è concava per x ∈ (- ∞ ; 0 ] e convessa per x ∈ [ 0 ; + ∞) ;
• il punto di flesso ha coordinate (0; 0), è anche lo zero della funzione;
• gli asintoti orizzontali sono linee rette y = - π 2 per x → - ∞ e y = π 2 per x → + ∞ (gli asintoti nella figura sono linee verdi).

1. Funzione arco cotangente: y = a r c c t g (x)

Definizione 25

Proprietà della funzione arco cotangente:

• dominio di definizione: x ∈ - ∞ ; +∞ ;
• intervallo: y ∈ (0 ; π) ;
• questa funzione è di tipo generale;
• la funzione è decrescente sull'intero dominio di definizione;
• la funzione arcocotangente è concava per x ∈ [ 0 ; + ∞) e convessità per x ∈ (- ∞ ; 0 ] ;
• il punto di flesso ha coordinate 0 ; π2;
• gli asintoti orizzontali sono le linee rette y = π in x → - ∞ (linea verde nel disegno) e y = 0 in x → + ∞.

Se noti un errore nel testo, evidenzialo e premi Ctrl+Invio

Funzione di alimentazione. Questa è la funzione: y = ascia n, dove un- permanente. In n= 1 otteniamo proporzionalità diretta: y = ascia; a n = 2 - parabola quadrata ; a n = - 1 - proporzionalità inversa o iperbole. Pertanto, queste funzioni sono casi speciali di una funzione di potenza. Sappiamo che la potenza zero di qualsiasi numero diverso da zero è 1, quindi, a n= 0 la funzione di potenza diventa una costante:y = un, cioè e. il suo programma è retta, asse parallelo X, esclusa l'origine (Spiega per favore, perché? ). Tutti questi casi (con un= 1 ) mostrato in Fig.13 (n 0 ) e Fig.14 ( n < 0). Отрицательные значения Xnon sono considerati qui come allora alcune funzioni:

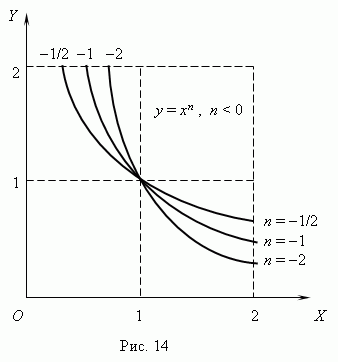
Se una n– intere, le funzioni di alimentazione hanno senso anche quandoX< 0, но их графики имеют различный вид в зависимости от того, является ли nun numero pari o un numero dispari. La Figura 15 mostra due di queste funzioni di alimentazione: per n= 2 e n = 3.


In n= 2 la funzione è pari eil suo grafico è simmetrico circa l'asse Y. In n= 3 la funzione è dispari e il suo grafico è simmetrico rispetto all'origine coordinate. Funzioney = X 3 chiamato parabola cubica.

La figura 16 mostra la funzione. Questo la funzione è parabola inversa a quadrata y = X 2 , il suo grafico si ottiene ruotando il grafico parabola quadrata intorno alla bisettrice del 1° angolo di coordinate. Questo è un modo per ottenere il grafico di qualsiasi funzione inversa dal grafico della sua funzione originale. Possiamo vedere dal grafico che questa è una funzione a due valori (questo è indicato anche dal segno ± davanti a radice quadrata). Tali funzioni non sono studiate nella matematica elementare, quindi, come funzione, di solito consideriamo uno dei suoi rami: superiore o inferiore.

Per prima cosa, prova a trovare l'ambito della funzione:

Sei riuscito? Confrontiamo le risposte:

Tutto ok? Ben fatto!

Ora proviamo a trovare l'intervallo della funzione:

Fondare? Confrontare:

Era d'accordo? Ben fatto!

Lavoriamo di nuovo con i grafici, solo che ora è un po' più difficile: trovare sia il dominio della funzione che l'intervallo della funzione.

Come trovare sia il dominio che l'intervallo di una funzione (avanzato)

Ecco cosa è successo:

Con la grafica, penso che tu l'abbia capito. Ora proviamo a trovare il dominio della funzione secondo le formule (se non sai come fare, leggi la sezione su):

Sei riuscito? Controllo risposte:

1. , poiché l'espressione radice deve essere maggiore o uguale a zero.
2. , poiché è impossibile dividere per zero e l'espressione radicale non può essere negativa.
3. , poiché, rispettivamente, per tutti.
4. perché non puoi dividere per zero.

Tuttavia, abbiamo ancora un momento che non è stato risolto ...

Vorrei ribadire la definizione e concentrarmi su di essa:

Si accorse? La parola "solo" è un elemento molto, molto importante della nostra definizione. Proverò a spiegarti sulle dita.

Diciamo di avere una funzione data da una retta. . A, sostituiamo dato valore nella nostra "regola" e lo otteniamo. Un valore corrisponde a un valore. Possiamo anche creare una tabella di vari valori e tracciare una determinata funzione per verificarlo.

"Aspetto! - dici, - "" si incontra due volte!" Quindi forse la parabola non è una funzione? No, lo è!

Il fatto che "" ricorra due volte è tutt'altro che un motivo per accusare la parabola di ambiguità!

Il fatto è che, calcolando, abbiamo ottenuto un gioco. E quando calcoliamo, abbiamo un gioco. Quindi è vero, la parabola è una funzione. Guarda il grafico:

Fatto? In caso contrario, ecco un esempio di vita reale per te, lontano dalla matematica!

Diciamo che abbiamo un gruppo di candidati che si sono incontrati durante la presentazione dei documenti, ognuno dei quali ha raccontato in una conversazione dove vive:

D'accordo, è abbastanza realistico che più ragazzi vivano nella stessa città, ma è impossibile che una persona viva in più città contemporaneamente. Questa è, per così dire, una rappresentazione logica della nostra "parabola" - Diverse x differenti corrispondono alla stessa y.

Ora facciamo un esempio in cui la dipendenza non è una funzione. Diciamo che questi stessi ragazzi hanno detto per quali specialità hanno fatto domanda:

Qui abbiamo una situazione completamente diversa: una persona può facilmente fare domanda per una o più direzioni. Questo è un elemento gli insiemi sono messi in corrispondenza più elementi imposta. Rispettivamente, non è una funzione.

Mettiamo alla prova le tue conoscenze nella pratica.

Determina dalle immagini cos'è una funzione e cosa non lo è:

Fatto? Ed ecco risposte:

• La funzione è - B,E.
• Non una funzione - A, B, D, D.

Ti chiedi perché? Sì, ecco perché:

In tutte le figure tranne A) e E) ce ne sono diversi per uno!

Sono sicuro che ora puoi facilmente distinguere una funzione da una non funzione, dire cos'è un argomento e cos'è una variabile dipendente e anche determinare l'ambito dell'argomento e l'ambito della funzione. Passiamo alla sezione successiva: come definire una funzione?

Modi per impostare una funzione

Cosa pensi significhino le parole "imposta funzione"? Esatto, significa spiegare a tutti di quale funzione stiamo parlando in questo caso. Inoltre, spiega in modo tale che tutti ti capiscano correttamente e che i grafici delle funzioni disegnati dalle persone secondo la tua spiegazione fossero gli stessi.

Come lo posso fare? Come impostare una funzione? Il modo più semplice, che è già stato utilizzato più di una volta in questo articolo: usando una formula. Scriviamo una formula e, sostituendovi un valore, calcoliamo il valore. E come ricorderete, una formula è una legge, una regola secondo la quale diventa chiaro a noi e ad un'altra persona come una X si trasformi in una Y.

Di solito, questo è esattamente quello che fanno: nelle attività vediamo funzioni già pronte definite da formule, tuttavia, ci sono altri modi per impostare una funzione che tutti dimenticano, e quindi la domanda "in quale altro modo puoi impostare una funzione?" confonde. Diamo un'occhiata a tutto in ordine e iniziamo con il metodo analitico.

Modo analitico per definire una funzione

Il metodo analitico è compito di una funzione che utilizza una formula. Questo è il modo più universale, completo e inequivocabile. Se hai una formula, allora sai assolutamente tutto sulla funzione: puoi creare una tabella di valori su di essa, puoi costruire un grafico, determinare dove la funzione aumenta e dove diminuisce, in generale, esplorala in toto.

Consideriamo una funzione. Cosa importa?

"Cosa significa?" - tu chiedi. Ti spiego ora.

Lascia che ti ricordi che nella notazione, l'espressione tra parentesi è chiamata argomento. E questo argomento può essere qualsiasi espressione, non necessariamente semplice. Di conseguenza, qualunque sia l'argomento (espressione tra parentesi), lo scriveremo invece nell'espressione.

Nel nostro esempio, sarà simile a questo:

Considera un'altra attività relativa al metodo analitico per specificare una funzione che avrai nell'esame.

Trova il valore dell'espressione, in.

Sono sicuro che all'inizio eri spaventato quando hai visto un'espressione del genere, ma non c'è assolutamente nulla di spaventoso in essa!

Tutto è come nell'esempio precedente: qualunque sia l'argomento (espressione tra parentesi), lo scriveremo invece nell'espressione. Ad esempio, per una funzione.

Cosa si dovrebbe fare nel nostro esempio? Invece, devi scrivere, e invece di -:

abbreviare l'espressione risultante:

È tutto!

Lavoro indipendente

Ora prova a trovare tu stesso il significato delle seguenti espressioni:

1. , Se
2. , Se

Sei riuscito? Confrontiamo le nostre risposte: Siamo abituati al fatto che la funzione ha la forma

Anche nei nostri esempi, definiamo la funzione in questo modo, ma analiticamente è possibile definire la funzione in modo implicito, ad esempio.

Prova a costruire tu stesso questa funzione.

Sei riuscito?

Ecco come l'ho costruito.

Con quale equazione siamo finiti?

Correttamente! Lineare, il che significa che il grafico sarà una linea retta. Facciamo una tabella per determinare quali punti appartengono alla nostra linea:

È proprio di questo che stavamo parlando... Uno corrisponde a molti.

Proviamo a disegnare cosa è successo:

Quello che abbiamo è una funzione?

Esatto, no! Come mai? Prova a rispondere a questa domanda con una foto. Cosa hai preso?

"Perché un valore corrisponde a più valori!"

Quale conclusione possiamo trarre da ciò?

Esatto, una funzione non può sempre essere espressa in modo esplicito e ciò che è "mascherato" da funzione non è sempre una funzione!

Modo tabulare di definire una funzione

Come suggerisce il nome, questo metodo è un piatto semplice. Si si. Come quello che abbiamo già fatto. Per esempio:

Qui hai immediatamente notato uno schema: Y è tre volte più grande di X. E ora il compito "pensa molto bene": pensi che una funzione data sotto forma di tabella sia equivalente a una funzione?

Non parliamo a lungo, ma disegniamo!

Così. Disegniamo una funzione data in entrambi i modi:

Vedi la differenza? Non si tratta di punti segnati! Dai un'occhiata più da vicino:

L'hai visto ora? Quando impostiamo la funzione in modo tabulare, riflettiamo sul grafico solo quei punti che abbiamo nella tabella e la linea (come nel nostro caso) passa solo attraverso di essi. Quando definiamo una funzione in modo analitico, possiamo prendere qualsiasi punto e la nostra funzione non si limita ad essi. Ecco una tale caratteristica. Ricorda!

Modo grafico per costruire una funzione

Modo grafico costruire una funzione non è meno conveniente. Disegniamo la nostra funzione e un'altra persona interessata può trovare ciò a cui y è uguale a una certa x, e così via. I metodi grafici e analitici sono tra i più comuni.

Tuttavia, qui devi ricordare di cosa abbiamo parlato all'inizio: non tutti gli "scarabocchi" disegnati nel sistema di coordinate sono una funzione! Ricordato? Per ogni evenienza, copierò qui la definizione di cosa sia una funzione:

Di norma, le persone di solito nominano esattamente questi tre modi per specificare una funzione che abbiamo analizzato: analitica (usando una formula), tabulare e grafica, dimenticando completamente che una funzione può essere descritta verbalmente. Come questo? Sì, molto facile!

Descrizione verbale della funzione

Come descrivere verbalmente la funzione? Prendiamo il nostro esempio recente - . Questa funzione può essere descritto come "ogni valore reale di x corrisponde al suo valore triplo". È tutto. Niente di complicato. Certo, obietterai: "ce ne sono così tanti funzioni complesse che è semplicemente impossibile chiedere verbalmente!” Sì, ce ne sono alcune, ma ci sono funzioni che sono più facili da descrivere verbalmente che da impostare con una formula. Ad esempio: "ogni valore naturale di x corrisponde alla differenza tra le cifre di cui è composto, mentre la cifra più grande contenuta nella voce del numero viene presa come minuendo". Consideriamo ora come viene implementata in pratica la nostra descrizione verbale della funzione:

La cifra più grande in un dato numero -, rispettivamente, - viene ridotta, quindi:

Principali tipi di funzioni

Ora passiamo al più interessante: considera i principali tipi di funzioni con cui hai lavorato / lavorerai e lavorerai nel corso della scuola e dell'istituto di matematica, cioè li conosceremo, per così dire, e li daremo breve descrizione. Maggiori informazioni su ciascuna funzione nella sezione corrispondente.

Funzione lineare

Una funzione della forma, dove, sono numeri reali.

Il grafico di questa funzione è una retta, quindi la costruzione funzione lineare si riduce a trovare le coordinate di due punti.

Posizione diretta su piano delle coordinate dipende dal fattore di pendenza.

Ambito della funzione (aka intervallo di argomenti) - .

L'intervallo di valori è .

funzione quadratica

Funzione del modulo, dove

Il grafico della funzione è una parabola, quando i rami della parabola sono diretti verso il basso, quando - verso l'alto.

Molte proprietà funzione quadratica dipendono dal valore del discriminante. Il discriminante è calcolato dalla formula

La posizione della parabola sul piano delle coordinate rispetto al valore e al coefficiente è mostrata in figura:

Dominio

L'intervallo di valori dipende dall'estremo della funzione data (il vertice della parabola) e dal coefficiente (la direzione dei rami della parabola)

Proporzionalità inversa

La funzione data dalla formula, dove

Il numero è chiamato fattore di proporzionalità inversa. A seconda del valore, i rami dell'iperbole sono in quadrati diversi:

Dominio - .

L'intervallo di valori è .

RIASSUNTO E FORMULA BASE

1. Una funzione è una regola secondo la quale ad ogni elemento di un insieme viene assegnato un elemento unico dell'insieme.

• - questa è una formula che denota una funzione, cioè la dipendenza di una variabile da un'altra;
• - variabile, o argomento;
• - valore dipendente - cambia quando cambia l'argomento, cioè secondo alcuni determinata formula, che riflette la dipendenza di una quantità dall'altra.

2. Valori di argomento validi, o l'ambito di una funzione, è ciò che è correlato al possibile in base al quale la funzione ha senso.

3. Intervallo di valori della funzione- ecco quali valori ci vogliono, con valori validi.

4. Esistono 4 modi per impostare la funzione:

• analitico (usando formule);
• tabulare;
• grafico
• descrizione verbale.

5. Principali tipi di funzioni:

• : , dove, sono numeri reali;
• : , dove;
• : , dove.

Università Nazionale delle Ricerche

Dipartimento di Geologia Applicata

Astratto su matematica superiore

Sul tema: "Funzioni elementari di base,

loro proprietà e grafici"

Completato:

Controllato:

insegnante

Definizione. La funzione data dalla formula y=a x (dove a>0, a≠1) è chiamata funzione esponenziale con base a.

Formuliamo le principali proprietà della funzione esponenziale:

1. Il dominio di definizione è l'insieme (R) di tutti i numeri reali.

2. L'intervallo di valori è l'insieme (R+) di tutti i numeri reali positivi.

3. Quando a > 1, la funzione aumenta su tutta la retta reale; a 0<а<1 функция убывает.

4. È una funzione generale.

, sull'intervallo xО [-3;3] , sull'intervallo xО [-3;3]

Una funzione della forma y(х)=х n , dove n è il numero ОR, è chiamata funzione di potenza. Il numero n può assumere diversi valori: sia intero che frazionario, sia pari che dispari. A seconda di ciò, la funzione di alimentazione avrà una forma diversa. Considera casi speciali che sono funzioni di potenza e riflettono le proprietà principali di questo tipo di curve nel seguente ordine: funzione di potenza y \u003d x² (una funzione con un esponente pari - una parabola), una funzione di potenza y \u003d x³ (una funzione con un esponente dispari - una parabola cubica) e funzione y \u003d √ x (x alla potenza di ½) (funzione con un esponente frazionario), una funzione con un esponente intero negativo (iperbole).

Funzione di alimentazione y=x²

1. D(x)=R – la funzione è definita sull'intero asse numerico;

2. E(y)= e aumenta sull'intervallo

Funzione di alimentazione y=x³

1. Il grafico della funzione y \u003d x³ è chiamato parabola cubica. La funzione di potenza y=x³ ha le seguenti proprietà:

2. D(x)=R – la funzione è definita sull'intero asse numerico;

3. E(y)=(-∞;∞) – la funzione assume tutti i valori nel suo dominio di definizione;

4. Quando x=0 y=0 – la funzione passa per l'origine O(0;0).

5. La funzione aumenta sull'intero dominio di definizione.

6. La funzione è dispari (simmetrica rispetto all'origine).

, sull'intervallo xн [-3;3]

A seconda del fattore numerico davanti a x³, la funzione può essere ripida/piatta e aumentare/diminuire.

Funzione di potenza con esponente negativo intero:

Se l'esponente n è dispari, il grafico di tale funzione di potenza è chiamato iperbole. Una funzione di potenza con esponente intero negativo ha le seguenti proprietà:

1. D(x)=(-∞;0)U(0;∞) per ogni n;

2. E(y)=(-∞;0)U(0;∞) se n è un numero dispari; E(y)=(0;∞) se n è un numero pari;

3. La funzione decresce sull'intero dominio di definizione se n è un numero dispari; la funzione aumenta sull'intervallo (-∞;0) e diminuisce sull'intervallo (0;∞) se n è un numero pari.

4. La funzione è dispari (simmetrica rispetto all'origine) se n è un numero dispari; una funzione è pari se n è un numero pari.

5. La funzione passa per i punti (1;1) e (-1;-1) se n è un numero dispari e per i punti (1;1) e (-1;1) se n è un numero pari.

, sull'intervallo xн [-3;3]

Funzione di potenza con esponente frazionario

Una funzione di potenza con esponente frazionario della forma (immagine) ha un grafico della funzione mostrata in figura. Una funzione di potenza con esponente frazionario ha le seguenti proprietà: (immagine)

1. D(x) ОR, se n è un numero dispari e D(x)= , sull'intervallo xО , sull'intervallo xО [-3;3]

La funzione logaritmica y \u003d log a x ha le seguenti proprietà:

1. Dominio di definizione D(x)н (0; + ∞).

2. Intervallo di valori E(y) О (- ∞; + ∞)

3. La funzione non è né pari né dispari (generale).

4. La funzione aumenta sull'intervallo (0; + ∞) per a > 1, diminuisce su (0; + ∞) per 0< а < 1.

Il grafico della funzione y = log a x può essere ottenuto dal grafico della funzione y = a x utilizzando una trasformazione di simmetria attorno alla retta y = x. Nella Figura 9 viene tracciato un grafico della funzione logaritmica per a > 1 e nella Figura 10 - per 0< a < 1.

; sull'intervallo xн ; sull'intervallo xО

Vengono chiamate le funzioni y \u003d sin x, y \u003d cos x, y \u003d tg x, y \u003d ctg x funzioni trigonometriche.

Le funzioni y \u003d sin x, y \u003d tg x, y \u003d ctg x sono dispari e la funzione y \u003d cos x è pari.

Funzione y \u003d sin (x).

1. Ambito di definizione D(x) ОR.

2. Intervallo di valori E(y) О [ - 1; uno].

3. La funzione è periodica; il periodo principale è 2π.

4. La funzione è dispari.

5. La funzione aumenta sugli intervalli [ -π/2 + 2πn; π/2 + 2πn] e decresce sugli intervalli [ π/2 + 2πn; 3π/2 + 2πn], n О Z.

Il grafico della funzione y \u003d sin (x) è mostrato nella Figura 11.