argomento :

Obbiettivo : Per farsi un'idea sulle derivate dell'inverso funzioni trigonometriche.

Compiti:

1. impara a trovare le derivate di queste funzioni,per elaborare con gli studenti la capacità di differenziare queste funzioni utilizzando
lavoro autonomo e controlli reciproci;

2. sviluppare un interesse per la matematica, l'informatica e cognitivo abilità,
la capacità di analizzare gli errori degli altri studenti;

3. coltivare la consapevolezza, l'indipendenza

1. Momento organizzativo
Saluto gli studenti, li presento alle regole di lavoro nella lezione, spiego come compilare correttamente la scheda di valutazione
2. Fase motivazionale
Gli studenti leggono ciò che devono sapere ed essere in grado di fare sull'argomento.
Prima di iniziare, leggi la regola RICORDA.
3. Fase operativa
Gli studenti completano il foglio di lavoro (allegato)
4. Riepilogo della lezione
Riflessione.

Oggi in classe:

Ho scoperto…

Era interessante…

Era difficile…

Sono riuscito…

Cercherò…

SCHEDA DI APPRENDIMENTO

su questo argomento: Derivate di funzioni trigonometriche e trigonometriche inverse.

2 lezioni.

COME RISULTATO DELLO STUDIO DELL'ARGOMENTO, È NECESSARIO

SAPERE: formule di differenziazione per funzioni trigonometriche e trigonometriche inverse.

ESSERE IN GRADO DI: trovare derivate di funzioni trigonometriche e trigonometriche inverse.

ricordare , che l'algoritmo deve funzionare.

Non dimenticare di superare il test, prendere appunti a margine, compilare la scheda di valutazione dell'argomento.

Si prega di non lasciare nessuna domanda senza risposta.

Sii obiettivo durante la revisione tra pari, aiuterà sia te che la persona che stai controllando.

TI AUGURO SUCCESSO!

w ADANIA №1

Leggi e impara le formule per differenziare le funzioni trigonometriche inverse: (2 pag.)

Se la funzione è complessa, allora

dove z – funzione elementare

Considera esempi:

y=arcosin(x) quindi y/=

y = arcctg(3x 2 -4) allora

si/=

Trova derivati:(3 pag.)

y= arcsin(-x) y= arctg(-x) y= arcos(2x)

P VAI A CONTROLLARE №1

w ADANIA №2

Risolvi uno qualsiasi degli esempi: (3b)

ma ) y = archi(5x - 3)

B ) y = arcctg(7x+1)

P VAI A CONTROLLARE №2

w ADANIA №3

a) Si consideri ancora la soluzione dell'esempio:

b) Trova le derivate di funzioni (4 p.)

arcosin(2x 2 - 5x)

arccos(4x 2 - 6x)

P VAI A CONTROLLARE №3

w ADANIA №4

Molto bene! Puoi iniziarelavoro di verifica numero 1.

ATTIVITÀ #5

a) Consideriamo la soluzione dell'esempio:

b) Trova le derivate di funzioni (6 p.)

P VAI A CONTROLLARE №5

Molto bene! Puoi iniziarelavoro di verifica numero 2.

LAVORO DI VERIFICA №1

Esegui una delle opzioni (11b)

1v 2v

1. Trova derivati seguenti funzioni:

a) 2 punti

y = arctg(-2x) y = arccos(3x)

b) 4 punti

y = archi(3x 2 - 2) y = arcctg(2x 3 +1)

c) 5 punti

y = arcoseno(x 2 - 5x) + tan (2x+1) y = arccos(3x 2 - 2x) + ctg(x+4) max

punti

ricevuto

punto

chi

controllato

grado

2 b

3 b

1 1 B

6 b

1 4 B

totale

43 b

TOTALE 43 punti

"5" - 33 - 43 punti;

"4" - 24 - 32 punti;

"3" - 18 - 23 punti.

Ecco una tabella riassuntiva per comodità e chiarezza durante lo studio dell'argomento.

Costantey=C

Funzione di potenza y = x p

(x p)" = p x p - 1

Funzione esponenzialey = x

(a x)" = a x ln a

In particolare, quandoa = enoi abbiamo y = ex

(e x)" = e x

funzione logaritmica

(log a x) " = 1 x ln a

In particolare, quandoa = enoi abbiamo y = log x

(ln x)" = 1 x

Funzioni trigonometriche

(peccato x) "= cos x (cos x)" = - sin x (t g x) " = 1 cos 2 x (c t g x)" = - 1 sin 2 x

Funzioni trigonometriche inverse

(a r c sin x) " = 1 1 - x 2 (a r c cos x) " = - 1 1 - x 2 (a r c t g x) " = 1 1 + x 2 (a r c c t g x) " = - 1 1 + x 2

Funzioni iperboliche

(s h x) " = c h x (c h x) " = s h x (t h x) " = 1 c h 2 x (c t h x) " = - 1 s h 2 x

Analizziamo come sono state ottenute le formule della tabella specificata, o, in altre parole, dimostreremo la derivazione di formule per derivate per ogni tipo di funzione.

Derivata di una costante

Prova 1

Per ricavare questa formula, prendiamo come base la definizione della derivata di una funzione in un punto. Usiamo x 0 = x, dove X assume il valore di qualsiasi numero reale, o, in altre parole, Xè un numero qualsiasi dal dominio della funzione f (x) = C . Scriviamo il limite del rapporto tra l'incremento della funzione e l'incremento dell'argomento come ∆ x → 0:

lim ∆ x → 0 ∆ f (x) ∆ x = lim ∆ x → 0 C - C ∆ x = lim ∆ x → 0 0 ∆ x = 0

Si noti che l'espressione 0 ∆ x rientra nel segno limite. Non è l'indeterminatezza dello “zero diviso per zero”, poiché il numeratore contiene non infinito piccolo valore, ovvero zero. In altre parole, l'incremento di una funzione costante è sempre zero.

Quindi, la derivata della funzione costante f (x) = C è uguale a zero sull'intero dominio di definizione.

Esempio 1

Date funzioni costanti:

f 1 (x) = 3 , f 2 (x) = un , un ∈ R , f 3 (x) = 4 . 13 7 22 , f 4 (x) = 0 , f 5 (x) = - 8 7

Soluzione

Descriviamo le condizioni date. Nella prima funzione vediamo la derivata del numero naturale 3 . Nell'esempio seguente, devi prendere la derivata di ma, dove ma- qualunque numero reale. Il terzo esempio ci dà la derivata numero irrazionale 4. 13 7 22 , il quarto - la derivata di zero (zero è un intero). Infine, nel quinto caso, abbiamo la derivata della frazione razionale - 8 7 .

Risposta: derivati impostare le funzioniè zero per ogni reale X(sull'intero dominio di definizione)

f 1 " (x) = (3) " = 0 , f 2 " (x) = (a) " = 0 , un ∈ R , f 3 "(x) = 4 . 13 7 22 " = 0 , f 4 " (x) = 0 " = 0 , f 5 " (x) = - 8 7 " = 0

Derivata della funzione di potenza

Passiamo a funzione di potenza e la formula della sua derivata, che ha la forma: (x p) " = p x p - 1, dove l'esponente Pè un numero reale.

Prova 2

Presentiamo la dimostrazione della formula quando l'esponente è numero naturale: p = 1 , 2 , 3 , …

Ancora una volta, ci basiamo sulla definizione di una derivata. Scriviamo il limite del rapporto tra l'incremento della funzione di potenza e l'incremento dell'argomento:

(x p) " = lim ∆ x → 0 = ∆ (x p) ∆ x = lim ∆ x → 0 (x + ∆ x) p - x p ∆ x

Per semplificare l'espressione al numeratore, utilizziamo la formula binomiale di Newton:

(x + ∆ x) p - x p = C p 0 + x p + C p 1 x p - 1 ∆ x + C p 2 x p - 2 (∆ x) 2 + . . . + + C pp - 1 x (∆ x) p - 1 + C pp (∆ x) p - xp = = C p 1 xp - 1 ∆ x + C p 2 xp - 2 (∆ x) 2 + . . . + C p p - 1 x (∆ x) p - 1 + C p p (∆ x) p

In questo modo:

(xp) " = lim ∆ x → 0 ∆ (xp) ∆ x = lim ∆ x → 0 (x + ∆ x) p - xp ∆ x = = lim ∆ x → 0 (C p 1 xp - 1 ∆ x + C p 2 xp - 2 (∆ x) 2 + . . . + C pp - 1 x (∆ x) p - 1 + C pp (∆ x) p) ∆ x = = lim ∆ x → 0 (C p 1 xp - 1 + C p 2 xp - 2 ∆ x + . . . + C pp - 1 x (∆ x) p - 2 + C pp (∆ x) p - 1) = = C p 1 xp - 1 + 0 + 0 + . . . + 0 = p! 1! (p - 1)! xp - 1 = p xp - 1

Quindi, abbiamo dimostrato la formula per la derivata di una funzione di potenza quando l'esponente è un numero naturale.

Prova 3

Dare prova per il caso quando P- qualsiasi numero reale diverso da zero, usiamo la derivata logaritmica (qui dovremmo capire la differenza dalla derivata della funzione logaritmica). Per avere una comprensione più completa, è desiderabile studiare la derivata della funzione logaritmica e inoltre trattare la derivata di una funzione data implicitamente e la derivata funzione complessa.

Considera due casi: quando X positivo e quando X sono negativi.

Quindi x > 0 . Allora: x p > 0 . Prendiamo il logaritmo dell'uguaglianza y \u003d x p alla base e e applichiamo la proprietà del logaritmo:

y = x p ln y = ln x p ln y = p ln x

A questo punto è stata ottenuta una funzione definita implicitamente. Definiamo la sua derivata:

(ln y) " = (p ln x) 1 y y " = p 1 x ⇒ y " = p y x = p x p x = p x p - 1

Consideriamo ora il caso quando X- un numero negativo

Se l'indicatore Pè un numero pari, allora la funzione potenza è definita anche per x< 0 , причем является четной: y (x) = - y ((- x) p) " = - p · (- x) p - 1 · (- x) " = = p · (- x) p - 1 = p · x p - 1

Quindi xp< 0 и возможно составить доказательство, используя логарифмическую производную.

Se Pè un numero dispari, allora la funzione potenza è definita per x< 0 , причем является нечетной: y (x) = - y (- x) = - (- x) p . Тогда x p < 0 , а значит логарифмическую производную задействовать нельзя. В такой ситуации возможно взять за основу доказательства правила дифференцирования и правило нахождения производной сложной функции:

y "(x) \u003d (- (- x) p) " \u003d - ((- x) p) " \u003d - p (- x) p - 1 (- x) " = \u003d p (- x ) p - 1 = p xp - 1

L'ultima transizione è possibile perché se Pè un numero dispari, quindi p - 1 o un numero pari o zero (per p = 1), quindi, per negativo X l'uguaglianza (- x) p - 1 = x p - 1 è vera.

Quindi, abbiamo dimostrato la formula per la derivata di una funzione di potenza per qualsiasi p reale.

Esempio 2

Funzioni date:

f 1 (x) = 1 x 2 3 , f 2 (x) = x 2 - 1 4 , f 3 (x) = 1 x log 7 12

Determina le loro derivate.

Soluzione

Trasformiamo parte delle funzioni date in una forma tabulare y = x p , in base alle proprietà del grado, e quindi utilizziamo la formula:

f 1 (x) \u003d 1 x 2 3 \u003d x - 2 3 ⇒ f 1 "(x) \u003d - 2 3 x - 2 3 - 1 \u003d - 2 3 x - 5 3 f 2 "(x) \u003d x 2 - 1 4 = 2 - 1 4 x 2 - 1 4 - 1 = 2 - 1 4 x 2 - 5 4 f 3 (x) = 1 x ceppo 7 12 = x - ceppo 7 12 ⇒ f 3 " ( x) = - ceppo 7 12 x - ceppo 7 12 - 1 = - ceppo 7 12 x - ceppo 7 12 - ceppo 7 7 = - ceppo 7 12 x - ceppo 7 84

Derivata di funzione esponenziale

Prova 4

Deriviamo la formula per la derivata, in base alla definizione:

(ax) " = lim ∆ x → 0 ax + ∆ x - ax ∆ x = lim ∆ x → 0 ax (a ∆ x - 1) ∆ x = ax lim ∆ x → 0 a ∆ x - 1 ∆ x = 0 0

Abbiamo l'incertezza. Per espanderlo, scriviamo una nuova variabile z = a ∆ x - 1 (z → 0 come ∆ x → 0). In questo caso a ∆ x = z + 1 ⇒ ∆ x = log a (z + 1) = ln (z + 1) ln a . Per l'ultima transizione viene utilizzata la formula per la transizione a una nuova base del logaritmo.

Eseguiamo una sostituzione nel limite originale:

(ax) " = ax lim ∆ x → 0 a ∆ x - 1 ∆ x = ax ln a lim ∆ x → 0 1 1 z ln (z + 1) = ax ln a lim ∆ x → 0 1 ln (z + 1) 1 z = ax ln a 1 ln lim ∆ x → 0 (z + 1) 1 z

Richiama il secondo meraviglioso limite e poi otteniamo la formula per la derivata funzione esponenziale:

(a x) " = a x ln a 1 ln lim z → 0 (z + 1) 1 z = a x ln a 1 ln e = a x ln a

Esempio 3

Le funzioni esponenziali sono date:

f 1 (x) = 2 3 x , f 2 (x) = 5 3 x , f 3 (x) = 1 (e) x

Dobbiamo trovare i loro derivati.

Soluzione

Usiamo la formula per la derivata della funzione esponenziale e le proprietà del logaritmo:

f 1 "(x) = 2 3 x" = 2 3 x ln 2 3 = 2 3 x (ln 2 - ln 3) f 2 "(x) = 5 3 x" = 5 3 x ln 5 1 3 = 1 3 5 3 x ln 5 f 3 "(x) = 1 (e) x" = 1 ex "= 1 ex ln 1 e = 1 ex ln e - 1 = - 1 ex

Derivata di una funzione logaritmica

Prova 5

Presentiamo la dimostrazione della formula per la derivata della funzione logaritmica per any X nel dominio di definizione e gli eventuali valori validi della base a del logaritmo. In base alla definizione della derivata si ottiene:

(log ax) " = lim ∆ x → 0 log a (x + ∆ x) - log ax ∆ x = lim ∆ x → 0 log ax + ∆ xx ∆ x = = lim ∆ x → 0 1 ∆ x log a 1 + ∆ xx = lim ∆ x → 0 log a 1 + ∆ xx 1 ∆ x = = lim ∆ x → 0 log a 1 + ∆ xx 1 ∆ x xx = lim ∆ x → 0 1 x log a 1 + ∆ xxx ∆ x = = 1 x log a lim ∆ x → 0 1 + ∆ xxx ∆ x = 1 x log ae = 1 x ln e ln a = 1 x ln a

Si può vedere dalla specifica catena di uguaglianze che le trasformazioni sono state costruite sulla base della proprietà del logaritmo. L'uguaglianza lim ∆ x → 0 1 + ∆ x x x ∆ x = e è vera secondo il secondo limite notevole.

Esempio 4

Le funzioni logaritmiche sono date:

f 1 (x) = log log 3 x , f 2 (x) = log x

È necessario calcolare le loro derivate.

Soluzione

Applichiamo la formula derivata:

f 1 "(x) = (log ln 3 x)" = 1 x ln (ln 3) ; f 2 "(x) \u003d (ln x)" \u003d 1 x ln e \u003d 1 x

Quindi la derivata del logaritmo naturale è divisa per X.

Derivate di funzioni trigonometriche

Prova 6

Ne usiamo alcuni formule trigonometriche e il primo limite notevole per derivare la formula per la derivata di una funzione trigonometrica.

Secondo la definizione della derivata della funzione seno, otteniamo:

(peccato x) " = lim ∆ x → 0 peccato (x + ∆ x) - peccato x ∆ x

La formula per la differenza dei seni ci consentirà di eseguire le seguenti azioni:

(peccato x) " = lim ∆ x → 0 sin (x + ∆ x) - sin x ∆ x = = lim ∆ x → 0 2 sin x + ∆ x - x 2 cos x + ∆ x + x 2 ∆ x = = lim ∆ x → 0 sin ∆ x 2 cos x + ∆ x 2 ∆ x 2 = = cos x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2

Infine, utilizziamo il primo meraviglioso limite:

sin "x = cos x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = cos x

Quindi la derivata della funzione peccato x volere cos x.

Dimostreremo anche la formula per la derivata del coseno allo stesso modo:

cos "x = lim ∆ x → 0 cos (x + ∆ x) - cos x ∆ x = = lim ∆ x → 0 - 2 sin x + ∆ x - x 2 sin x + ∆ x + x 2 ∆ x = = - lim ∆ x → 0 sin ∆ x 2 sin x + ∆ x 2 ∆ x 2 = = - sin x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = - sin x

Quelli. sarà la derivata della funzione cos x – peccato x.

Deriviamo le formule per le derivate della tangente e della cotangente in base alle regole di differenziazione:

tg "x = sin x cos x" = sin "x cos x - sin x cos" x cos 2 x = = cos x cos x - sin x (- sin x) cos 2 x = sin 2 x + cos 2 x cos 2 x = 1 cos 2 xctg "x = cos x sin x" = cos "x sin x - cos x sin" x sin 2 x = = - sin x sin x - cos x cos x sin 2 x = - sin 2 x + cos 2 x peccato 2 x = - 1 peccato 2 x

Derivate di funzioni trigonometriche inverse

Sezione derivati funzioni inverse fornisce informazioni complete sulla dimostrazione delle formule per le derivate dell'arcoseno, dell'arcocoseno, dell'arcotangente e dell'arcocotangente, quindi non duplichiamo il materiale qui.

Derivati di funzioni iperboliche

Prova 7

Possiamo derivare formule per le derivate del seno iperbolico, coseno, tangente e cotangente usando la regola di differenziazione e la formula per la derivata della funzione esponenziale:

sh "x = ex - e - x 2" = 1 2 ex " - e - x " == 1 2 ex - - e - x = ex + e - x 2 = chxch " x = ex + e - x 2" = 1 2 ex "+ e - x" == 1 2 ex + - e - x = ex - e - x 2 = shxth "x = shxchx" = sh "x chx - shx ch" xch 2 x = ch 2 x - sh 2 xch 2 x = 1 ch 2 xcth "x = chxshx" = ch "x shx - chx sh" xsh 2 x = sh 2 x - ch 2 xsh 2 x = - 1 sh 2 x

Se noti un errore nel testo, evidenzialo e premi Ctrl+Invio

Per trovare derivata di una funzione trigonometrica bisogno di usare tavola derivata, vale a dire derivati 6-13.

Quando trovato derivate di semplici funzioni trigonometriche Per evitare errori comuni, prestare attenzione ai seguenti punti:

in un'espressione di funzione, uno dei termini è spesso seno, coseno o altre funzioni trigonometriche non dall'argomento della funzione, ma dal numero (costante), quindi la derivata di questo termine è uguale a zero;
quasi sempre è necessario semplificare l'espressione ottenuta come risultato della differenziazione e per questo è necessario utilizzare con sicurezza la conoscenza delle operazioni con le frazioni;
per semplificare l'espressione, è quasi sempre necessario conoscere identità trigonometriche, come la formula del doppio angolo e la formula dell'unità come somma dei quadrati di seno e coseno.

Esempio 1 Trova la derivata di una funzione

Soluzione. Diciamo con derivata del coseno tutto è chiaro, diranno molti che iniziano a studiare i derivati. Che ne dici di derivata seno dodici diviso per pi? Risposta: considera uguale a zero! Qui il seno (dopotutto una funzione!) è una trappola, perché l'argomento non è la variabile x o qualsiasi altra variabile, ma solo un numero. Cioè, anche il seno di questo numero è un numero. E la derivata di un numero (costante), come sappiamo dalla tabella delle derivate, è uguale a zero. Quindi, lasciamo solo il seno negativo di x e troviamo la sua derivata, senza dimenticare il segno:

Esempio 2 Trova la derivata di una funzione

Soluzione. Il secondo termine è lo stesso caso del primo termine nell'esempio precedente. Cioè, un numero e la derivata del numero è zero. Troviamo la derivata del secondo termine come derivata del quoziente:

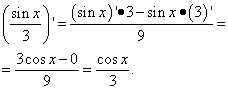
Esempio 3 Trova la derivata di una funzione

Soluzione. Questo è un compito diverso: qui nel primo termine non c'è né un arcoseno né un'altra funzione trigonometrica, ma c'è x, il che significa che questa è una funzione di x. Pertanto, lo differenziamo come termine nella somma delle funzioni:

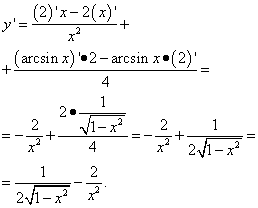
Qui, erano richieste abilità nelle azioni con le frazioni, vale a dire nell'eliminazione della frazione a tre piani.

Esempio 4 Trova la derivata di una funzione

Soluzione. Qui la lettera "fi" svolge lo stesso ruolo di "x" nei casi precedenti (e nella maggior parte degli altri, ma non in tutti) - una variabile indipendente. Pertanto, quando cerchiamo la derivata del prodotto delle funzioni, non ci affretteremo a dichiarare la derivata della radice di "phi" uguale a zero. Così:

Ma la soluzione non finisce qui. Poiché i membri simili sono raccolti in due parentesi, abbiamo ancora bisogno di trasformare (semplificare) l'espressione. Pertanto, moltiplichiamo le parentesi per i fattori presi da esse, quindi riduciamo i termini a un denominatore comune ed eseguiamo altre trasformazioni elementari:

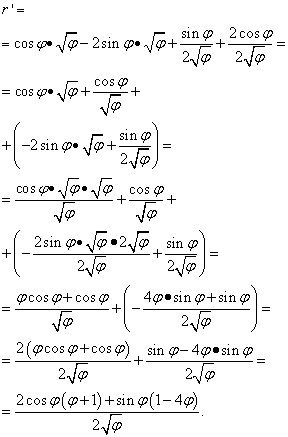
Esempio 5 Trova la derivata di una funzione

Soluzione. In questo esempio, avremo bisogno di conoscere il fatto che esiste una tale funzione trigonometrica - secante - e le sue formule in termini di coseno. Differenziare:

Esempio 6 Trova la derivata di una funzione

Soluzione. In questo esempio, dovremo ricordare la formula del doppio angolo del corso scolastico. Ma prima, distinguiamo:

(questa è la formula del doppio angolo)

Calcolo differenziale di una funzione di una variabile

1. introduzione

Analisi matematica- una branca della matematica che ha preso forma nel 18° secolo e comprende due parti principali: calcolo differenziale e integrale. La derivata di una funzione è uno dei concetti matematici di base Calcolo differenziale. L'analisi è nata grazie agli sforzi di molti matematici (prima di tutto, I. Newton e G. Leibniz) e ha svolto un ruolo enorme nello sviluppo delle scienze naturali: un metodo potente e abbastanza universale per studiare le funzioni che sorgono quando si risolvono vari problemi applicati è apparso.

2. Funzione numerica. Schema di studio della funzione.

(Vedi note sull'argomento "Funzione Power")

1) Ambito della funzione.

2) Insieme dei valori delle funzioni.

3) Funzioni pari, dispari.

4) Monotonia della funzione.

5) Reversibilità della funzione.

6) Funzione zeri.

7) Intervalli di costanza di segno di una funzione.

8) Funzione limitata.

Esercizi:

Trova l'ambito di una funzione:

ma) ; B) ; in) .

ma) ; B) ; G) .

3. Il concetto di limite di una funzione in un punto.

Considera i grafici di alcune funzioni. Studiamo il comportamento delle funzioni vicino al punto x 0 , cioè in qualche quartiere del punto x 0 .

Riso. 1. Fig. 2. Fig. 3.

La funzione ha una proprietà che la distingue dalle altre due funzioni.

1. Quando ci si avvicina all'argomento X a x 0 a sinistra ea destra, i valori corrispondenti della funzione sono arbitrariamente vicini allo stesso numero MA.

Le altre due funzioni non hanno questa proprietà.

2. Quando ci si avvicina all'argomento X a x 0 a sinistra, i valori corrispondenti della funzione sono arbitrariamente vicini al numero MA, e quando ci si avvicina all'argomento X a x 0 a destra, i valori corrispondenti della funzione sono arbitrariamente vicini al numero IN.

3. Funzione quando ci si avvicina a un argomento X a x 0 sinistra e destra assumono valori diversi.

Produzione: Se quando ci si avvicina all'argomento X a x 0 a sinistra ea destra, i punti con coordinate sono arbitrariamente vicini al punto con coordinate , quindi .

Esempio: Fa la funzione limite ai punti x 1, x 2, x 3, x 4, x 5?

Risposta: Funzione ha un limite nei punti x 1 , x 3 ;

funzione non ha limite ai punti x 2 , x 4 , x 5 .

Commento:

4. Definizione di una funzione continua in un punto e su un intervallo

Il concetto di continuità di una funzione è convenientemente associato all'idea del grafico di questa funzione come una linea "continua" (continua). Una linea continua è una linea tracciata senza sollevare la matita dal foglio.

Domanda: quale di queste funzioni è continua?

Riso. 1. Fig. 2. Fig. 3.

Riso. 4. Fig. cinque.

Risposta: Di queste funzioni, la funzione mostrata in Fig. 1 è continua. N. 3, poiché il suo grafico è una linea "continua" (continua).

Domanda: Quali sono le proprietà della funzione mostrata in Fig. No. 3, e non hanno altre funzioni?

Risposta:

1. La funzione è definita nel punto x 0. Questa proprietà non vale per la funzione mostrata in fig. n. 1.

2. C'è un limite finito della funzione nel punto x 0. Questa proprietà non vale per le funzioni illustrate in fig. N. 2, 5.

3. Il limite della funzione nel punto x 0 è uguale al valore della funzione in questo punto, cioè . Questa proprietà non vale per la funzione mostrata in fig. n. 4.

Le proprietà soddisfatte per la funzione mostrata in fig. 3, e permettono di definire una funzione continua in un punto x 0 .

Definizione: La funzione si dice continua in un punto x 0, Se .

Commento: Se la funzione è continua in un punto x 0, quindi punta x 0 si dice punto di continuità di una funzione se la funzione non è continua nel punto x 0, quindi punta x 0 è chiamato punto di interruzione della funzione.

Definizione: Una funzione si dice continua su un intervallo se è continua in ogni punto di quell'intervallo.

5. Incremento argomento, incremento funzione

Sia data la funzione .

x 0 - il valore iniziale dell'argomento, ;

X- valore finale dell'argomento, ;

f (x 0) - il valore iniziale della funzione;

f(x 0 + D x) - il valore finale della funzione.

Definizione: La differenza tra i valori finali e iniziali dell'argomento è chiamata incremento dell'argomento. D x \u003d x - x 0

Definizione: La differenza tra i valori finali e iniziali della funzione è chiamata incremento della funzione. D y \u003d f (x 0 + D x) - f (x 0)

Commento:

Incremento geometrico dell'argomento D x– è la differenza tra le ascisse dei punti del grafico della funzione corrispondenti ai valori finali e iniziali dell'argomento.
Funzione di incremento geometrico D y– è la differenza tra le ordinate dei punti del grafico della funzione corrispondenti ai valori finali e iniziali dell'argomento.
L'incremento dell'argomento e l'incremento della funzione possono essere positivi o negativi.

6. Il concetto di derivata di una funzione. significato fisico funzione derivata

Si consideri il problema della velocità di variazione della funzione , dove X e a può essere qualsiasi quantità fisica.

x 0 - il valore iniziale dell'argomento; f (x 0) - il valore iniziale della funzione;

x 0 +D x - valore finale dell'argomento; f(x 0 + D x) - valore finale della funzione;

D y \u003d f (x 0 + D x) - f (x 0) - incremento della funzione;

– tasso medio di variazione di una funzione in un intervallo Dx .

– velocità di variazione istantanea di una funzione, velocità di variazione di una funzione in un punto x 0.

Definizione: Derivata di una funzione in un punto x 0è chiamato limite del rapporto di incremento D funziona in un punto x 0 per incrementare Dx argomento quando l'incremento dell'argomento tende a zero.

Produzione: Derivata di una funzione in un punto x 0è la velocità di variazione della funzione nel punto x 0.

Teorema: Derivata di una funzione costante y = c in qualsiasi punto è uguale a zero.

Teorema: Derivata di una funzione y = x in qualsiasi punto uguale a uno .

Commento: Trovare la derivata di una data funzione si chiama differenziazione.

7. Regole per differenziare la somma, il prodotto, il quoziente delle funzioni

Considera la funzione , costituito da altre due funzioni e, avendo derivate sull'intervallo:

3) .

Teorema #1: La derivata della somma (differenza) di due funzioni è uguale alla somma (differenza) delle derivate di queste funzioni.

Esempio: Calcola la derivata di una funzione

Teorema #2: La derivata del prodotto di due funzioni è determinata dalla formula:

Conseguenza: Il fattore costante può essere estratto dal segno della derivata: .

Prova: .

Esempio

Esercizi:

2) ;

La derivata della funzione di potenza at è calcolata dalla formula:

Commento: La formula è valida per una funzione di potenza con qualsiasi esponente. ,

Esempio: Calcola derivate di funzioni:

Produzione: .

Esercizi: Calcola derivate di funzioni:

; 2) ; 3) ;

4) ; 5) ;

6) ; 7) .

Teorema #3: La derivata del quoziente di due funzioni è determinata dalla formula:

Conseguenze: ;

Esempio: Calcola derivate di funzioni:

2) . .

3) . .

Esercizi: Calcola derivate di funzioni:

1. ; 2. ; 3. ;

4. ; 5. ; 6.

;

; 8. ; 9.

8. Il concetto di funzione complessa

Regola di differenziazione di funzioni complesse

Sia definita la funzione sull'insieme, e la funzione sull'insieme, e per, il valore corrispondente. Quindi viene definita una funzione sull'insieme, che viene chiamata funzione complessa da X (funzione da funzione).

Una variabile è chiamata argomento intermedio di una funzione complessa.

Esempio:

Esercizi:

Da cosa funzioni elementari Queste funzioni complesse sono costituite da:

1) ; 2) ;

; 4) .

Componi funzioni complesse da queste funzioni elementari:

1) , ; 2) , ;

3) , . 4) , , .

Produzione: La derivata di una funzione complessa è uguale al prodotto delle derivate delle funzioni elementari che la compongono .

Esempio: Calcola derivate di funzioni:

- potenza, lineare; , .

- potenza, quadratica; , .

Esercizi: Calcola derivate di funzioni:

1. ; 2.

;

3. ; 4. ;

; 6. .

9. Derivata di funzioni esponenziali, logaritmiche

Esempio: Calcola derivate di funzioni:

1. . .

2. . .

3. . .

Esempio: Calcola derivate di funzioni:

1. . .

2. . .

Esercizi: Calcola la derivata di una funzione:

1. ; 2. ; 3. ;

4. ; 5. ; 6. ;

7. ; 8. .

10. Derivate di funzioni trigonometriche

Derivate di funzioni trigonometriche inverse

Esempio: Calcola derivate di funzioni:

1. . .

2. . .

Un compito

. .

Un compito: Calcola la derivata della funzione.

L'esercizio: Calcola la derivata della funzione.

Derivate di funzioni trigonometriche inverse

;

Esercizi: Calcola derivate di funzioni:

1. 2.

3. 4.

5. 6. 7. 8. 9.

10.

11. 12. 13.

11. senso geometrico funzione derivata

Consideriamo una funzione.

Prendi un punto fisso sul grafico della funzione e un punto arbitrario . Disegniamo una secante . Se il punto m sposta indefinitamente fino a un punto M0 secondo il grafico della funzione , quindi la secante M 0 M occuperà posizioni diverse e se il punto coincide m con un punto M0 la secante prenderà la posizione limite M O T , quindi la retta M O T sarà tangente al grafico della funzione nel punto M0 .

Definizione: Tangente al grafico della funzione al punto M0 chiamato limite M O T secante mentre si lotta per un punto m secondo il programma al punto M0.

B- angolo di inclinazione della secante M 0 M

un- angolo di inclinazione della tangente M O T nella direzione positiva dell'asse x.

Pendenza della secante M 0 M .

Pendenza tangente M O T .

Considera un triangolo rettangolo M 0 MA (). Tangente ad angolo acuto triangolo rettangolo uguale al rapporto tra la gamba opposta e l'adiacente:

Cioè . E questo significa .

Definire la derivata della funzione in un punto x 0 : .

, , Di conseguenza, .

Produzione: Il significato geometrico della derivata della funzione è che la derivata della funzione a è uguale alla pendenza della tangente tracciata al grafico della funzione nel punto con l'ascissa.

Esempio:

1. Trova la pendenza della tangente tracciata nel grafico della funzione in punti .

; ; ; ; ; .

Risposta: ; ; .

2. Trova l'angolo di inclinazione della tangente tracciata nel grafico della funzione nel punto con l'ascissa.

; ; ; ; . parallela a una retta;

Installiamo condizione necessaria l'esistenza di un estremo.

Il teorema di Fermat: Se il punto interno x 0 fuori portata funzione continuaè un punto estremo e a questo punto c'è una derivata, quindi è uguale a zero.

Commento: Tuttavia, l'uguaglianza a zero della derivata della funzione nel punto x 0 ancora non dà il diritto di rivendicarlo x 0 – punto estremo della funzione.

Nel derivare la primissima formula della tabella, si procederà dalla definizione della derivata di una funzione in un punto. Portiamo dove X- qualsiasi numero reale, cioè X– qualsiasi numero dall'area di definizione della funzione. Scriviamo il limite del rapporto tra la funzione incremento e l'argomento incremento in:

Si noti che sotto il segno del limite si ottiene un'espressione, che non è l'incertezza di zero divisa per zero, poiché il numeratore non contiene un valore infinitesimo, ma appunto zero. In altre parole, l'incremento di una funzione costante è sempre zero.

In questo modo, derivata di una funzione costanteè uguale a zero sull'intero dominio di definizione.

Derivata di una funzione di potenza.

La formula per la derivata di una funzione di potenza ha la forma , dove l'esponente Pè un numero reale.

Proviamo prima la formula dell'esponente naturale, cioè per p = 1, 2, 3, ...

Useremo la definizione di derivata. Scriviamo il limite del rapporto tra l'incremento della funzione potenza e l'incremento dell'argomento:

Per semplificare l'espressione al numeratore, passiamo alla formula binomiale di Newton:

Di conseguenza,

Ciò dimostra la formula per la derivata di una funzione di potenza per un esponente naturale.

Derivata di funzione esponenziale.

Deriviamo la formula della derivata in base alla definizione:

È arrivato all'incertezza. Per espanderlo, introduciamo una nuova variabile e per . Quindi . Nell'ultima transizione, abbiamo utilizzato la formula per la transizione a una nuova base del logaritmo.

Eseguiamo una sostituzione nel limite originale:

Se ricordiamo il secondo limite notevole, arriviamo alla formula per la derivata della funzione esponenziale:

Derivata di una funzione logaritmica.

Dimostriamo la formula per la derivata della funzione logaritmica per tutti X dall'ambito e tutti i valori di base validi un logaritmo. Per definizione della derivata si ha:

Come hai notato, nella dimostrazione le trasformazioni sono state effettuate utilizzando le proprietà del logaritmo. Uguaglianza è valido per il secondo limite notevole.

Derivate di funzioni trigonometriche.

Per derivare formule per derivate di funzioni trigonometriche, dovremo richiamare alcune formule trigonometriche, oltre al primo limite notevole.

Per definizione della derivata per la funzione seno, abbiamo .

Usiamo la formula per la differenza dei seni:

Resta da volgere al primo notevole limite:

Quindi la derivata della funzione peccato x mangiare cos x.

La formula per la derivata del coseno si dimostra esattamente allo stesso modo.

Pertanto, la derivata della funzione cos x mangiare –peccato x.

La derivazione delle formule per la tavola delle derivate per la tangente e la cotangente sarà effettuata utilizzando le comprovate regole di differenziazione (derivata di una frazione).

Derivati di funzioni iperboliche.

Le regole di differenziazione e la formula per la derivata della funzione esponenziale dalla tabella delle derivate consentono di derivare formule per le derivate del seno iperbolico, coseno, tangente e cotangente.

Derivata della funzione inversa.

Affinché non ci sia confusione nella presentazione, indichiamo nell'indice inferiore l'argomento della funzione con cui viene eseguita la differenziazione, ovvero è la derivata della funzione f(x) su X.

Ora formuliamo regola per trovare la derivata della funzione inversa.

Passiamo alle funzioni y = f(x) e x = g(y) reciprocamente inverse, definite sugli intervalli e rispettivamente. Se in un punto esiste una derivata finita diversa da zero della funzione f(x), allora nel punto esiste una derivata finita della funzione inversa g(y), e . In un'altra voce .

Questa regola può essere riformulata per chiunque X dall'intervallo , quindi otteniamo .

Verifichiamo la validità di queste formule.

Troviamo la funzione inversa per il logaritmo naturale (qui yè una funzione, e X- discussione). Risolvere questa equazione per X, otteniamo (qui Xè una funzione, e y la sua argomentazione). Cioè, e funzioni reciprocamente inverse.

Dalla tabella delle derivate, lo vediamo e .

Assicuriamoci che le formule per trovare le derivate della funzione inversa ci portino agli stessi risultati:

Come puoi vedere, abbiamo ottenuto gli stessi risultati della tabella delle derivate.

Ora abbiamo le conoscenze per dimostrare formule per derivate di funzioni trigonometriche inverse.

Iniziamo con la derivata dell'arcoseno.

. Quindi, dalla formula per la derivata della funzione inversa, otteniamo

Resta da eseguire la trasformazione.

Poiché l'intervallo dell'arcoseno è l'intervallo , poi (vedi la sezione sulle funzioni elementari di base, le loro proprietà ei grafici). Pertanto, non consideriamo.