Senso
Più grande
Senso
Meno
Punto massimo
Punto basso
I compiti di trovare i punti estremi della funzione vengono risolti secondo lo schema standard in 3 passaggi.
Passo 1. Trova la derivata di una funzione
- Memorizzare le formule derivate funzioni elementari e le regole di base della differenziazione per trovare la derivata.
y′(x)=(x3−243x+19)′=3x2−243.
Passo 2. Trova gli zeri della derivata
- Risolvi l'equazione risultante per trovare gli zeri della derivata.
3x2−243=0⇔x2=81⇔x1=−9,x2=9.
Passaggio 3. Trova i punti estremi
- Utilizzare il metodo della spaziatura per determinare i segni della derivata;
- Nel punto minimo, la derivata è zero e cambia segno da meno a più, e nel punto massimo, da più a meno.
Applichiamo questo approccio per risolvere il seguente problema:
Trova il punto massimo della funzione y=x3−243x+19.
1) Trova la derivata: y′(x)=(x3−243x+19)′=3x2−243;
2) Risolvi l'equazione y′(x)=0: 3x2−243=0⇔x2=81⇔x1=−9,x2=9;
3) La derivata è positiva per x>9 e x<−9 и отрицательная при −9 Come trovare il valore più grande e più piccolo di una funzione Per risolvere il problema di trovare i valori più grandi e più piccoli della funzione necessario: Aiuta in molte attività teorema: Se c'è un solo punto estremo sul segmento, e questo è il punto minimo, allora in esso viene raggiunto il valore più piccolo della funzione. Se questo è il punto massimo, allora viene raggiunto il valore massimo. 14. Il concetto e le proprietà fondamentali dell'integrale indefinito. Se la funzione f(X X, e K- numero, quindi In breve: la costante può essere estratta dal segno di integrale. Se funziona f(X) e g(X) hanno antiderivate sull'intervallo X, poi In breve: l'integrale della somma è uguale alla somma degli integrali. Se la funzione f(X) ha un'antiderivata sull'intervallo X, quindi per i punti interni di questo intervallo: In breve: la derivata dell'integrale è uguale all'integrando. Se la funzione f(X) è continuo sull'intervallo X ed è differenziabile in punti interni di questo intervallo, quindi: In breve: l'integrale del differenziale di una funzione è uguale a quella funzione più la costante di integrazione. Diamo una definizione matematica rigorosa concetti di integrale indefinito. L'espressione gentile è chiamata integrale della funzione f(x)
, dove f(x)
- funzione integranda, data (nota), dx
- differenziale X
, con simbolo sempre presente dx
. Definizione. Integrale indefinito chiamata funzione F(x) + C
, contenente una costante arbitraria C
, il cui differenziale è uguale a integrando espressione f(x)dx
, cioè. Richiama questo - differenziale di funzione ed è così definito: Trovare problema integrale indefinitoè trovare una funzione derivato che è uguale all'integrando. Questa funzione è determinata fino a una costante, perché la derivata della costante è zero. Ad esempio, è noto che , quindi si scopre che Trovare il compito integrale indefinito dalle funzioni non è così semplice e facile come sembra a prima vista. In molti casi, ci deve essere abilità nel lavorare con integrali indefiniti, dovrebbe essere un'esperienza che viene con la pratica e costante risolvere esempi di integrali indefiniti. Vale la pena considerare il fatto che integrali indefiniti da alcune funzioni (ce ne sono parecchie) non vengono prese in funzioni elementari. 15. Tabella degli integrali indefiniti di base. Formule di base 16. Integrale definito come limite della somma integrale. Significato geometrico e fisico dell'integrale. Sia definita la funzione y=ƒ(x) sul segmento [a; gruppo musicale< b. Выполним следующие действия. 1. Usando i punti x 0 \u003d a, x 1, x 2, ..., x n \u003d B (x 0 2. In ogni segmento parziale , i = 1,2,...,n, scegliamo un punto arbitrario con i є e calcoliamo il valore della funzione in esso, cioè il valore ƒ(con i). 3. Moltiplicare il valore trovato della funzione ƒ (da i) per la lunghezza ∆x i =x i -x i-1 del corrispondente segmento parziale: ƒ (da i) ∆х i. 4. Componi la somma S n di tutti questi prodotti: La somma della forma (35.1) è chiamata somma integrale della funzione y \u003d ƒ (x) sul segmento [a; b]. Indichiamo con λ la lunghezza del segmento parziale più grande: λ = max ∆x i (i = 1,2,..., n). 5. Trova il limite della somma integrale (35.1) come n → ∞ tale che λ→0. Se, inoltre, la somma integrale S n ha un limite I, che non dipende dal metodo di partizionamento del segmento [a; b] in segmenti parziali, o dalla scelta dei punti in essi, allora il numero I si dice integrale definito della funzione y = ƒ(x) sul segmento [a; b] ed è indicato così, I numeri aeb sono detti rispettivamente limite inferiore e superiore di integrazione, ƒ(x) - l'integrando, ƒ(x) dx - l'integrando, x - la variabile di integrazione, il segmento [a; b] - area (segmento) di integrazione. La funzione y \u003d ƒ (x), per la quale sul segmento [a; b] c'è un integrale definito, detto integrabile su questo intervallo. Formuliamo ora il teorema di esistenza per un integrale definito. Teorema 35.1 (Cauchy). Se la funzione y = ƒ(x) è continua sul segmento [a; b], quindi l'integrale definito Si noti che la continuità di una funzione è condizione sufficiente per la sua integrabilità. Tuttavia, un integrale definito può esistere anche per alcune funzioni discontinue, in particolare per qualsiasi funzione che è limitata su un intervallo e ha un numero finito di punti di discontinuità su di esso. Segnaliamo alcune proprietà dell'integrale definito che derivano direttamente dalla sua definizione (35.2). 1. L'integrale definito è indipendente dalla notazione della variabile di integrazione: Ciò deriva dal fatto che la somma integrale (35.1) e, di conseguenza, il suo limite (35.2) non dipendono da quale lettera denota l'argomento di questa funzione. 2. Un integrale definito con gli stessi limiti di integrazione è uguale a zero: 3. Per qualsiasi numero reale c. 17. Formula di Newton-Leibniz. Proprietà fondamentali di un integrale definito. Lascia che la funzione y = f(x) continuo sul segmento
e F(x)è una delle antiderivate della funzione su questo segmento, quindi Formula di Newton-Leibniz: Si chiama la formula di Newton-Leibniz la formula base del calcolo integrale. Per dimostrare la formula di Newton-Leibniz, abbiamo bisogno del concetto di integrale con limite superiore variabile. Se la funzione y = f(x) continuo sul segmento
, quindi l'integrale della forma per l'argomento è una funzione del limite superiore. Denotiamo questa funzione Scriviamo infatti l'incremento della funzione corrispondente all'incremento dell'argomento e utilizziamo la quinta proprietà dell'integrale definito e il corollario della decima proprietà: Riscriviamo questa uguaglianza nella forma Calcolare Fa), utilizzando la prima proprietà dell'integrale definito: L'incremento di una funzione è generalmente indicato come Per applicare la formula di Newton-Leibniz, ci basta conoscere una delle antiderivate y=F(x) integrando y=f(x) sul segmento
e calcolare l'incremento di tale antiderivata su questo segmento. Nell'articolo vengono analizzati i metodi di integrazione delle principali modalità di reperimento dell'antiderivata. Diamo alcuni esempi di calcolo di integrali definiti usando la formula di Newton-Leibniz per chiarimenti. Esempio. Calcola il valore dell'integrale definito usando la formula di Newton-Leibniz. Decisione. Innanzitutto, si noti che l'integrando è continuo sull'intervallo
, quindi, è integrabile su di esso. (Abbiamo parlato di funzioni integrabili nella sezione sulle funzioni per le quali esiste un integrale definito). Dalla tabella degli integrali indefiniti si evince che per una funzione l'insieme delle antiderivate per tutti i valori reali dell'argomento (e quindi per ) si scrive come . Prendiamo il primitivo C=0: . Ora resta da usare la formula di Newton-Leibniz per calcolare l'integrale definito: 18. Applicazioni geometriche di un integrale definito. APPLICAZIONI GEOMETRICHE DI UN INTEGRALE DEFINITO Calcolo del volume corporeo Calcolo del volume corporeo da aree note di sezioni parallele: Volume del corpo di rotazione: ; . Esempio 1. Trova l'area di una figura delimitata da una curva y=sinx, linee rette Decisione: Trovare l'area della figura: Esempio 2. Calcola l'area di una figura delimitata da linee Decisione: Troviamo le ascisse dei punti di intersezione dei grafici di queste funzioni. Per fare questo, risolviamo il sistema di equazioni Da qui troviamo x 1 \u003d 0, x 2 \u003d 2.5. 19. Concetto di controlli differenziali. Equazioni differenziali del primo ordine. Equazione differenziale- un'equazione che collega il valore della derivata di una funzione con la funzione stessa, i valori della variabile indipendente, i numeri (parametri). L'ordine delle derivate incluse nell'equazione può essere diverso (formalmente non è limitato da nulla). Derivati, funzioni, variabili indipendenti e parametri possono essere inclusi nell'equazione in varie combinazioni, oppure tutte le derivate tranne almeno una possono essere del tutto assenti. Nessuna equazione contenente derivate di una funzione sconosciuta è un'equazione differenziale. Per esempio, Equazioni differenziali parziali(URCHP) sono equazioni contenenti funzioni sconosciute di più variabili e loro derivate parziali. La forma generale di tali equazioni può essere rappresentata come: dove sono variabili indipendenti ed è una funzione di queste variabili. L'ordine delle equazioni differenziali alle derivate parziali può essere determinato allo stesso modo delle equazioni differenziali ordinarie. Un'altra importante classificazione delle equazioni alle derivate parziali è la loro divisione in equazioni di tipo ellittico, parabolico e iperbolico, specialmente per le equazioni del secondo ordine. Sia le equazioni differenziali ordinarie che le equazioni differenziali alle derivate parziali possono essere suddivise in lineare e non lineare. Un'equazione differenziale è lineare se la funzione incognita e le sue derivate entrano nell'equazione solo alla prima potenza (e non si moltiplicano tra loro). Per tali equazioni, le soluzioni formano un sottospazio affine dello spazio delle funzioni. La teoria delle equazioni differenziali lineari è stata sviluppata molto più profondamente della teoria delle equazioni non lineari. Forma generale di un'equazione differenziale lineare n-esimo ordine: dove pi(X) sono funzioni note della variabile indipendente, dette coefficienti dell'equazione. Funzione r(X) sul lato destro viene chiamato membro libero(l'unico termine che non dipende dalla funzione incognita) Un'importante classe particolare di equazioni lineari sono le equazioni differenziali lineari con coefficienti costanti. Una sottoclasse di equazioni lineari sono omogeneo equazioni differenziali - equazioni che non contengono un termine libero: r(X) = 0. Per equazioni differenziali omogenee vale il principio di sovrapposizione: una combinazione lineare di soluzioni particolari di tale equazione sarà anche la sua soluzione. Vengono chiamate tutte le altre equazioni differenziali lineari eterogeneo equazioni differenziali. Le equazioni differenziali non lineari nel caso generale non hanno sviluppato metodi risolutivi, ad eccezione di alcune classi particolari. In alcuni casi (con l'uso di alcune approssimazioni) possono essere ridotti a quelli lineari. Ad esempio, l'equazione lineare di un oscillatore armonico · è un'equazione differenziale omogenea del secondo ordine a coefficienti costanti. La soluzione è una famiglia di funzioni, dove e sono costanti arbitrarie, che per una soluzione specifica sono determinate da condizioni iniziali specificate separatamente. Questa equazione, in particolare, descrive il moto di un oscillatore armonico con una frequenza ciclica di 3. · La seconda legge di Newton può essere scritta sotto forma di equazione differenziale · L'equazione differenziale di Bessel è un'equazione ordinaria lineare omogenea del secondo ordine a coefficienti variabili: le sue soluzioni sono le funzioni di Bessel. Un esempio di equazione differenziale ordinaria non lineare non omogenea del 1° ordine: Nel seguente gruppo di esempi, la funzione sconosciuta tu dipende da due variabili X e t o X e y. Equazione differenziale parziale lineare omogenea del primo ordine: Equazione d'onda unidimensionale - un'equazione lineare omogenea in derivate parziali del tipo iperbolico del secondo ordine con coefficienti costanti, descrive la vibrazione della corda, se - la deviazione della corda in un punto con coordinate X al tempo t, e il parametro un imposta le proprietà della stringa: L'equazione di Laplace nello spazio bidimensionale è un'equazione differenziale lineare omogenea in derivate parziali del secondo ordine di tipo ellittico a coefficienti costanti, che si pone in molti problemi fisici di meccanica, conduzione del calore, elettrostatica, idraulica: L'equazione di Korteweg-de Vries, un'equazione differenziale parziale del terzo ordine non lineare che descrive le onde stazionarie non lineari, inclusi i solitoni: 20. Equazioni differenziali con applicabili separabili. Equazioni lineari e metodo di Bernoulli. Un'equazione differenziale lineare del primo ordine è un'equazione lineare rispetto a una funzione sconosciuta e alla sua derivata. Ha la forma di un grado intero. Infatti, se troviamo e sostituiamo nelle equazioni dei tipi considerati, otteniamo l'uguaglianza corretta. Come notato nell'articolo su equazioni omogenee, se per condizione è richiesto di trovare solo una soluzione particolare, allora la funzione, per ovvi motivi, non ci dà fastidio, ma quando è richiesto di trovare una soluzione/integrale generale, allora è necessario assicurarsi che questa funzione sia non perso! Ho portato tutte le varietà popolari dell'equazione di Bernoulli in una grande borsa con i regali e ho proceduto alla distribuzione. Appendi i calzini sotto l'albero. Esempio 1 Trova una soluzione particolare dell'equazione differenziale corrispondente alla condizione iniziale data. Probabilmente, molti sono rimasti sorpresi dal fatto che il primo regalo sia stato immediatamente tirato fuori dalla borsa insieme Problema di Cauchy. Questo non è un incidente. Quando un'equazione di Bernoulli viene proposta per una soluzione, per qualche motivo è spesso necessario trovare una soluzione particolare. Nella mia raccolta, ho condotto un campione casuale di 10 equazioni di Bernoulli e la soluzione generale (senza una soluzione particolare) deve essere trovata solo in 2 equazioni. Ma, in realtà, questa è una sciocchezza, poiché la soluzione generale andrà comunque cercata. Decisione: Questa differenza ha la forma , e quindi è l'equazione di Bernoulli Il valore più grande della funzione Il valore più piccolo della funzione Come ha detto il padrino: "Niente di personale". Solo derivati! L'attività 12 nelle statistiche è considerata abbastanza difficile e tutto perché i ragazzi non hanno letto questo articolo (scherzo). Nella maggior parte dei casi, la colpa è della negligenza. 12 compito è di due tipi: Compiti con l'esame: Trova il punto massimo della funzione Trova il punto minimo della funzione Compiti con l'esame: Trova il valore più grande della funzione sull'intervallo [−4; -1] Risposta: -6 Trova il valore più grande della funzione sul segmento Risposta: 11 Risultati: Il punto estremo di una funzione è il punto nel dominio della funzione in cui il valore della funzione assume un valore minimo o massimo. I valori della funzione in questi punti sono chiamati estremi (minimo e massimo) della funzione. Definizione. Punto X1
ambito della funzione f(X) è chiamato punto massimo della funzione
, se il valore della funzione a questo punto è maggiore dei valori della funzione in punti sufficientemente vicini ad essa, situati a destra e a sinistra di essa (cioè la disuguaglianza f(X0
) > f(X 0
+ Δ X)
X1
massimo. Definizione. Punto X2
ambito della funzione f(X) è chiamato punto minimo della funzione, se il valore della funzione a questo punto è minore dei valori della funzione in punti sufficientemente vicini ad essa, situati a destra e a sinistra di essa (cioè la disuguaglianza f(X0
) < f(X 0
+ Δ X)
). In questo caso, si dice che la funzione ha al punto X2
minimo. Diciamo il punto X1
- punto massimo della funzione f(X). Poi nell'intervallo fino a X1
la funzione aumenta, quindi la derivata della funzione è maggiore di zero ( f "(X) > 0 ), e nell'intervallo successivo X1
la funzione sta diminuendo, quindi derivata di funzione minore di zero ( f "(X) < 0
).
Тогда в точке X1
Assumiamo anche che il punto X2
- punto minimo della funzione f(X). Poi nell'intervallo fino a X2
la funzione è decrescente e la derivata della funzione è minore di zero ( f "(X) < 0
), а в интервале
после X2
la funzione è crescente e la derivata della funzione è maggiore di zero ( f "(X) > 0 ). In questo caso anche al punto X2
la derivata della funzione è zero o non esiste. teorema di Fermat ( caratteristica necessaria l'esistenza di un estremo della funzione). Se punto X0
- punto estremo della funzione f(X), allora a questo punto la derivata della funzione è uguale a zero ( f "(X) = 0 ) o non esiste. Definizione. Vengono chiamati i punti in cui la derivata di una funzione è uguale a zero o non esiste punti critici
. Esempio 1 Consideriamo una funzione. Al punto X= 0 la derivata della funzione è uguale a zero, quindi il punto X= 0 è il punto critico. Tuttavia, come si può vedere sul grafico della funzione, aumenta nell'intero dominio di definizione, quindi il punto X= 0 non è un punto estremo di questa funzione. Quindi, le condizioni che la derivata di una funzione in un punto sia uguale a zero o non esista sono condizioni necessarie per un estremo, ma non sufficienti, poiché si possono dare altri esempi di funzioni per le quali queste condizioni sono soddisfatte, ma la funzione non ha un estremo nel punto corrispondente. Così deve avere sufficienti indicazioni, che consentono di giudicare se esiste un extremum in un particolare punto critico e quale: un massimo o un minimo. Teorema (il primo criterio sufficiente per l'esistenza di un estremo di una funzione). Punto critico X0
f(X) , se la derivata della funzione cambia segno passando per questo punto, e se il segno cambia da "più" a "meno", allora il punto massimo, e se da "meno" a "più", allora il punto minimo . Se vicino al punto X0
, a sinistra ea destra di essa, la derivata mantiene il suo segno, ciò significa che la funzione o decresce o aumenta solo in qualche intorno del punto X0
. In questo caso, al punto X0
non c'è l'estremo. Così, per determinare i punti estremi della funzione, è necessario effettuare le seguenti operazioni
: Esempio 2 Trova gli estremi di una funzione Decisione. Troviamo la derivata della funzione: Uguaglia la derivata a zero per trovare i punti critici: Poiché per qualsiasi valore di "x" il denominatore non è uguale a zero, eguagliamo il numeratore a zero: Ho un punto critico X= 3. Determiniamo il segno della derivata negli intervalli delimitati da questo punto: nell'intervallo da meno infinito a 3 - segno meno, ovvero la funzione diminuisce, nell'intervallo da 3 a più infinito - un segno più, ovvero la funzione aumenta. Cioè, punto X= 3 è il punto minimo. Trova il valore della funzione nel punto minimo: Quindi si trova il punto estremo della funzione: (3; 0) , ed è il punto minimo. Teorema (il secondo criterio sufficiente per l'esistenza di un estremo di una funzione). Punto critico X0
è il punto estremo della funzione f(X), se la derivata seconda della funzione a questo punto non è uguale a zero ( f ""(X) ≠ 0 ), inoltre, se la derivata seconda è maggiore di zero ( f ""(X) > 0 ), quindi il punto massimo e se la derivata seconda è minore di zero ( f ""(X) < 0
),
то точкой минимума. Osservazione 1. Se in un punto X0
sia la prima che la seconda derivata svaniscono, quindi a questo punto è impossibile giudicare la presenza di un estremo sulla base del secondo segno sufficiente. In questo caso, è necessario utilizzare il primo criterio sufficiente per l'estremo della funzione. Osservazione 2. Anche il secondo criterio sufficiente per l'estremo di una funzione è inapplicabile quando la derivata prima non esiste nel punto stazionario (quindi non esiste nemmeno la derivata seconda). In questo caso è necessario utilizzare anche il primo criterio sufficiente per l'estremo della funzione. Dalle definizioni di cui sopra segue che l'estremo di una funzione è di natura locale - questo è il valore più grande e più piccolo della funzione rispetto ai valori più vicini. Supponiamo di considerare i tuoi guadagni in un arco di tempo di un anno. Se a maggio hai guadagnato 45.000 rubli, ad aprile 42.000 rubli e a giugno 39.000 rubli, i guadagni di maggio sono il massimo della funzione di guadagno rispetto ai valori più vicini. Ma a ottobre hai guadagnato 71.000 rubli, a settembre 75.000 rubli ea novembre 74.000 rubli, quindi i guadagni di ottobre sono il minimo della funzione di guadagno rispetto ai valori vicini. E si vede facilmente che il massimo tra i valori di aprile-maggio-giugno è inferiore al minimo di settembre-ottobre-novembre. In generale, una funzione può avere diversi estremi in un intervallo e può risultare che qualsiasi minimo della funzione è maggiore di qualsiasi massimo. Quindi, per la funzione mostrata nella figura sopra, . Cioè, non si deve pensare che il massimo e il minimo della funzione siano, rispettivamente, i suoi valori massimo e minimo sull'intero segmento in esame. Nel punto massimo, la funzione ha il valore massimo solo rispetto a quei valori che ha in tutti i punti sufficientemente vicini al punto massimo, e nel punto minimo, il valore più piccolo solo rispetto a quei valori che ha in tutti i punti sufficientemente vicino al punto minimo. Pertanto, possiamo affinare il concetto di punti estremi di una funzione data sopra e chiamare i punti minimi punti di minimo locale e i punti di massimo - punti di massimo locale. Esempio 3 Soluzione La funzione è definita e continua sull'intera linea dei numeri. Il suo derivato Per l'intervallo, il punto di riferimento può essere : troviamo . Prendendo un punto nell'intervallo, otteniamo e prendendo un punto nell'intervallo, abbiamo . Quindi, negli intervalli e , e nell'intervallo . Secondo il primo segno sufficiente extremum, non c'è un estremo nel punto (poiché la derivata mantiene il suo segno nell'intervallo ), e nel punto la funzione ha un minimo (poiché la derivata cambia segno da meno a più quando passa per questo punto). Trova i valori corrispondenti della funzione: , e . Nell'intervallo, la funzione diminuisce, poiché in questo intervallo, e nell'intervallo aumenta, poiché in questo intervallo. Per chiarire la costruzione del grafico, troviamo i punti di intersezione di esso con gli assi coordinati. Quando otteniamo un'equazione di cui si trovano le radici e , cioè due punti (0; 0) e (4; 0) del grafico della funzione. Utilizzando tutte le informazioni ricevute, costruiamo un grafico (vedi all'inizio dell'esempio). Per l'autocontrollo durante i calcoli, è possibile utilizzare calcolatore di derivati online . Esempio 4 Trova gli estremi della funzione e costruisci il suo grafico. Il dominio della funzione è l'intera retta dei numeri, ad eccezione del punto, cioè . Per abbreviare lo studio, possiamo usare il fatto che questa funzione è pari, poiché Trovare la derivata 1) 2) ma la funzione subisce un'interruzione a questo punto, quindi non può essere un punto estremo. Così, data funzione presenta due punti critici: e . Tenendo conto della parità della funzione, controlliamo solo il punto dal secondo segno sufficiente dell'estremo. Per fare questo, troviamo la derivata seconda Per avere un quadro più completo del grafico della funzione, scopriamo il suo comportamento ai confini del dominio di definizione: (qui il simbolo indica il desiderio X a zero a destra, e X rimane positivo; allo stesso modo significa aspirazione X a zero a sinistra, e X rimane negativo). Quindi, se , allora . Successivamente, troviamo quelli. se poi . Il grafico della funzione non ha punti di intersezione con gli assi. L'immagine è all'inizio dell'esempio. Per l'autocontrollo durante i calcoli, è possibile utilizzare calcolatore di derivati online . Esempio 8 Trova gli estremi della funzione. Decisione. Trova il dominio della funzione. Poiché la disuguaglianza deve valere, otteniamo da . Troviamo la derivata prima della funzione. Teorema.
(condizione necessaria per l'esistenza di un extremum) Se la funzione f (x) è differenziabile nel punto x \u003d x 1 e il punto x 1 è un punto estremo, la derivata della funzione svanisce a questo punto. Prova.
Supponiamo che la funzione f(x) abbia un massimo nel punto x = x 1. Quindi, per Dх>0 positivo sufficientemente piccolo, vale la seguente disuguaglianza: A-priorità: Quelli. se Dх®0, ma Dх<0, то f¢(x 1) ³ 0, а если Dх®0, но Dх>0, quindi f¢(x 1) £ 0. E questo è possibile solo se a Dх®0 f¢(x 1) = 0. Nel caso in cui la funzione f(x) abbia un minimo nel punto x 2, il teorema è dimostrato in modo simile. Il teorema è stato dimostrato. Conseguenza.
Non è vero il contrario. Se la derivata di una funzione in un punto è uguale a zero, ciò non significa che la funzione abbia un estremo in questo punto. Un esempio eloquente di ciò è la funzione y \u003d x 3, la cui derivata nel punto x \u003d 0 è uguale a zero, ma a questo punto la funzione ha solo un'inflessione e non un massimo o un minimo. Definizione. punti critici Le funzioni sono punti in cui la derivata della funzione non esiste o è uguale a zero. Il teorema sopra considerato ci fornisce le condizioni necessarie per l'esistenza di un extremum, ma questo non basta. Esempio: f(x) = ôxô Esempio: f(x) = Nel punto x = 0 la funzione ha un minimo, ma nel punto x = 0 la funzione non ha nessuno dei due non ha derivati. massimo, nessun minimo, no In generale, la funzione f(x) può avere un estremo nei punti in cui la derivata non esiste o è uguale a zero. Teorema.
(Condizioni sufficienti l'esistenza di un estremo) Sia la funzione f(x) continua nell'intervallo (a, b), che contiene il punto critico x 1 , e differenziabile in tutti i punti di tale intervallo (tranne, forse, il punto x 1 stesso). Se, passando per il punto x 1 da sinistra a destra, la derivata della funzione f¢(x) cambia di segno da “+” a “-“, allora nel punto x = x 1 la funzione f(x) ha un massimo, e se la derivata cambia segno da “- “ a “+” - allora la funzione ha un minimo. Prova.
Lascia stare Secondo il teorema di Lagrange: f(x) - f(x 1) = f¢(e)(x - x 1), dove x< e < x 1 . Allora: 1) Se x< x 1 , то e < x 1 ; f¢(e)>0; f¢(e)(x – x 1)<0, следовательно f(x) – f(x 1)<0 или f(x) < f(x 1). 2) Se x > x 1, allora e > x 1 f¢(e)<0; f¢(e)(x – x 1)<0, следовательно f(x) – f(x 1)<0 или f(x) < f(x 1). Poiché le risposte sono le stesse, possiamo dire che f(x)< f(x 1) в любых точках вблизи х 1 , т.е. х 1 – точка максимума. La dimostrazione del teorema per il punto di minimo è simile. Il teorema è stato dimostrato. Sulla base di quanto sopra, è possibile sviluppare un'unica procedura per trovare il più grande e il valore più piccolo funzioni sul segmento: 1) Trova i punti critici della funzione. 2) Trova i valori della funzione nei punti critici. 3) Trova i valori della funzione alle estremità del segmento. 4) Scegli tra i valori ottenuti il più grande e il più piccolo. Indagine di una funzione a un uso estremo derivati di ordini superiori. Sia f¢(x 1) = 0 nel punto x = x 1 e sia f¢¢(x 1) esistente e continua in qualche intorno del punto x 1 . Teorema.
Se f¢(x 1) = 0, allora la funzione f(x) nel punto x = x 1 ha un massimo se f¢¢(x 1)<0 и минимум, если f¢¢(x 1)>0.
Prova.
Sia f¢(x 1) = 0 e f¢¢(x 1)<0. Т.к. функция f(x) непрерывна, то f¢¢(x 1) будет отрицательной и в некоторой малой окрестности точки х 1 . Perché f¢¢(x) = (f¢(x))¢< 0, то f¢(x) убывает на отрезке, содержащем точку х 1 , но f¢(x 1)=0, т.е. f¢(x) >0 a x Per il caso di una funzione minima, il teorema è dimostrato in modo simile. Se f¢¢(x) = 0, la natura del punto critico è sconosciuta. Sono necessarie ulteriori ricerche per determinarlo. Convessità e concavità di una curva. Punti di flessione. Definizione.
La curva è convessa su sull'intervallo (a, b) se tutti i suoi punti giacciono al di sotto di una qualsiasi delle sue tangenti su questo intervallo. Si chiama una curva con un punto convesso verso l'alto convesso, e si chiama la curva convessa verso il basso concavo. La figura mostra un'illustrazione della definizione di cui sopra. Teorema 1.
Se in tutti i punti dell'intervallo (a, b) la derivata seconda della funzione f(x) è negativa, allora la curva y = f(x) è convessa in alto (convessa). Prova.
Sia x 0 О (a, b). Disegna una tangente alla curva in questo punto. Equazione della curva: y = f(x); Equazione tangente: Deve essere dimostrato che . Secondo il teorema di Lagrange per f(x) – f(x 0): , x 0< c < x. Secondo il teorema di Lagrange per Sia x > x 0 quindi x 0< c 1 < c < x. Т.к. x – x 0 >0 e c - x 0 > 0 e, inoltre, per condizione Quindi, . Sia x< x 0 тогда x < c < c 1 < x 0 и x – x 0 < 0, c – x 0 < 0, т.к. по условию то Similmente si può dimostrare che se f¢¢(x) > 0 sull'intervallo (a, b), allora la curva y=f(x) è concava sull'intervallo (a, b). Il teorema è stato dimostrato. Definizione.
Viene chiamato il punto che separa la parte convessa della curva dalla parte concava punto di flesso. Ovviamente, nel punto di flesso, la tangente interseca la curva. Teorema 2.
Sia la curva definita dall'equazione y = f(x). Se la derivata seconda f¢¢(a) = 0 oppure f¢¢(a) non esiste e passando per il punto x = a f¢¢(x) cambia segno, allora il punto della curva con l'ascissa x = a è un punto di flesso. Prova.
1) Sia f¢¢(x)< 0 при х < a и f¢¢(x) >0 per x > a. Poi a X< a кривая выпукла, а при x >una curva è concava, cioè il punto x = a è il punto di flesso. 2) Sia f¢¢(x) > 0 per x< b и f¢¢(x) < 0 при x < b. Тогда при x < b кривая обращена выпуклостью вниз, а при x >b - rigonfiarsi. Allora x = b è un punto di flesso. Il teorema è stato dimostrato. Asintoti. Nello studio delle funzioni accade spesso che quando la coordinata x di un punto di una curva viene rimossa all'infinito, la curva si avvicini indefinitamente a una certa retta. Definizione.
Chiamato diretto asintoto curva, se la distanza dal punto variabile della curva a questa retta tende a zero quando il punto viene rimosso all'infinito. Va notato che non tutte le curve hanno un asintoto. Gli asintoti possono essere dritti o obliqui. Lo studio delle funzioni per la presenza di asintoti ha Grande importanza e consente di determinare con maggiore precisione la natura della funzione e il comportamento del grafico della curva. In generale, la curva, avvicinandosi indefinitamente al suo asintoto, può intersecarlo, e non in un punto, come mostrato nel grafico della funzione sottostante Consideriamo più in dettaglio i metodi per trovare gli asintoti delle curve. Asintoti verticali. Dalla definizione dell'asintoto consegue che se o o , allora la retta x = a è l'asintoto della curva y = f(x). Ad esempio, per una funzione, la linea x = 5 è l'asintoto verticale. Asintoti obliqui. Si supponga che la curva y = f(x) abbia un asintoto obliquo y = kx + b. Designiamo il punto di intersezione della curva e la perpendicolare all'asintoto - M, P - il punto di intersezione di questa perpendicolare con l'asintoto. L'angolo tra l'asintoto e l'asse x sarà indicato con j. La perpendicolare MQ all'asse x interseca l'asintoto nel punto N. Allora MQ = y è l'ordinata del punto della curva, NQ = è l'ordinata del punto N sull'asintoto. A condizione: , РNMP = j, . L'angolo j è costante e non uguale a 90 0 , quindi Quindi Quindi, la linea y = kx + b è un asintoto della curva. Per definizione esatta questa linea, è necessario trovare un modo per calcolare i coefficienti k e b. Nell'espressione risultante, prendiamo x tra parentesi: Perché x®¥, quindi Quindi Perché Si noti che gli asintoti orizzontali sono un caso speciale di asintoti obliqui per k = 0. Esempio. 1) Asintoti verticali: y®+¥ x®0-0: y®-¥ x®0+0, quindi x = 0 è un asintoto verticale. 2) Asintoti obliqui: Pertanto, la retta y = x + 2 è un asintoto obliquo. Tracciamo la funzione: Esempio. Trova gli asintoti e traccia il grafico della funzione. Le linee x=3 e x=-3 sono gli asintoti verticali della curva. Trova gli asintoti obliqui: y = 0 è l'asintoto orizzontale. Esempio. Trova gli asintoti e traccia il grafico della funzione La linea x = -2 è l'asintoto verticale della curva. Troviamo gli asintoti obliqui. In totale, la linea y = x - 4 è un asintoto obliquo. Schema di studio della funzione Il processo di ricerca di una funzione consiste in diverse fasi. Per un'idea più completa del comportamento della funzione e della natura del suo grafico, è necessario trovare: 1) L'ambito della funzione. Questo concetto include sia il dominio dei valori che l'ambito di una funzione. 2) Punti di interruzione. (Se sono disponibili). 3) Intervalli di aumento e diminuzione. 4) Punti di massimo e minimo. 5) Massimo e valore minimo funzioni nel suo dominio. 6) Aree di convessità e concavità. 7) Punti di flesso (se presenti). 8) Asintoti (se presenti). 9) Costruire un grafico. Usiamo questo schema con un esempio. Esempio. Esamina la funzione e traccia il suo grafico. Troviamo l'area di esistenza della funzione. È ovvio che dominio di definizione funzione è l'area (-¥; -1) È (-1; 1) È (1; ¥). A sua volta, si può vedere che le linee x = 1, x = -1 sono asintoti verticali storto. Area di valore di questa funzione è l'intervallo (-¥; ¥). punti di interruzione le funzioni sono i punti x=1, x=-1. Noi troviamo punti critici. Troviamo la derivata della funzione Punti critici: x = 0; x = - ; x = ; x = -1; x = 1. Troviamo la derivata seconda della funzione Determiniamo la convessità e la concavità della curva agli intervalli. -¥ < x < - , y¢¢ < 0, кривая выпуклая - < x < -1, y¢¢ < 0, кривая выпуклая 1 < x < 0, y¢¢ >0, curva concava 0 < x < 1, y¢¢ < 0, кривая выпуклая 1 < x < , y¢¢ >0, curva concava < x < ¥, y¢¢ >0, curva concava Trovare lacune crescente e discendente funzioni. Per fare ciò, determiniamo i segni della derivata della funzione sugli intervalli. -¥ < x < - , y¢ >0, la funzione è in aumento - < x < -1, y¢ < 0, функция убывает 1 < x < 0, y¢ < 0, функция убывает 0 < x < 1, y¢ < 0, функция убывает 1 < x < , y¢ < 0, функция убывает < x < ¥, y¢¢ >0, la funzione è in aumento Si può vedere che il punto x = - è un punto massimo, e il punto x = è il punto minimo. I valori della funzione in questi punti sono rispettivamente -3/2 e 3/2. A proposito di verticale asintotiè già stato detto sopra. Ora troviamo asintoti obliqui. Quindi, l'equazione dell'asintoto obliquo è y = x. Costruiamo orario caratteristiche: Funzioni di più variabili
Quando si considerano le funzioni di più variabili, ci si limita a una descrizione dettagliata delle funzioni di due variabili, poiché tutti i risultati ottenuti saranno validi per le funzioni numero arbitrario variabili. Definizione: se a ciascuna coppia di numeri indipendenti (x, y) di un determinato insieme, secondo una regola, vengono assegnati uno o più valori della variabile z, allora la variabile z viene chiamata funzione di due variabili. Definizione:
Se una coppia di numeri (x, y) corrisponde a un valore di z, viene chiamata la funzione inequivocabile, e se più di uno, allora - ambiguo. Definizione: Ambito di definizione la funzione z è l'insieme di coppie (x, y) per le quali esiste la funzione z. Definizione: Punto di quartiere M 0 (x 0, y 0) di raggio r è l'insieme di tutti i punti (x, y) che soddisfano la condizione Definizione:
Viene chiamato il numero A limite funzione f(x, y) poiché il punto M(x, y) tende al punto M 0 (x 0, y 0), se per ogni numero e > 0 esiste un numero tale r > 0 che per ogni punto M (x, y) per cui la condizione anche la condizione è vera Annota: Definizione:
Sia il punto M 0 (x 0, y 0) appartenente al dominio della funzione f(x, y). Quindi viene chiamata la funzione z = f(x, y). continuo nel punto M 0 (x 0, y 0), se inoltre, il punto M(x, y) tende al punto M 0 (x 0, y 0) in modo arbitrario. Se la condizione (1) non è soddisfatta in nessun momento, allora questo punto viene chiamato punto di rottura funzioni f(x, y). Questo può essere nei seguenti casi: 1) La funzione z \u003d f (x, y) non è definita nel punto M 0 (x 0, y 0). 2) Non c'è limite. 3) Questo limite esiste, ma non è uguale a f(x 0 , y 0). Proprietà.
Se la funzione f(x, y, …) è definita e continua in modo chiuso e area delimitata D, allora in quest'area c'è almeno un punto N(x 0 , y 0 , …) tale che la disuguaglianza f(x 0 , y 0 , …) ³ f(x, y, …) così come un punto N 1 (x 01 , y 01 , ...), tale che per tutti gli altri punti la disuguaglianza è vera f(x 01 , y 01 , …) £ f(x, y, …) allora f(x 0 , y 0 , …) = M – valore più alto funzioni e f(x 01 , y 01 , ...) = m - valore più piccolo funzioni f(x, y, …) nel dominio D. Una funzione continua in un dominio chiuso e limitato D raggiunge almeno una volta il suo valore massimo e una volta il suo valore minimo. Proprietà.
Se la funzione f(x, y, ...) è definita e continua in un dominio limitato chiuso D, e M e m sono rispettivamente i valori più grandi e più piccoli della funzione in questo dominio, allora per ogni punto m О c'è è un punto N 0 (x 0 , y 0 , …) tale che f(x 0 , y 0 , …) = m. In poche parole, funzione continua prende nella regione D tutti i valori intermedi tra M e m. Una conseguenza di questa proprietà può essere la conclusione che se i numeri M e m hanno segni diversi, allora nel dominio D la funzione svanisce almeno una volta. Proprietà.
Funzione f(x, y, …), continua in un dominio chiuso D, limitato in quest'area, se esiste un numero K tale che per tutti i punti dell'area la disuguaglianza è vera Proprietà.
Se una funzione f(x, y, …) è definita e continua in un dominio chiuso D, allora essa uniformemente continuo in questo settore, cioè per chiunque numero positivo e esiste un numero D > 0 tale che per due punti qualsiasi (x 1 , y 1) e (x 2 , y 2) dell'area situata a distanza minore di D, la disuguaglianza Le proprietà di cui sopra sono simili alle proprietà delle funzioni di una variabile che sono continue su un intervallo. Vedere Proprietà delle funzioni Continua su un intervallo. Derivate e differenziali di funzioni più variabili. Definizione.
Sia data una funzione z = f(x, y) in qualche dominio. Prendi un punto arbitrario M(x, y) e imposta l'incremento Dx sulla variabile x. Quindi viene chiamata la quantità D x z = f(x + Dx, y) – f(x, y) incremento parziale della funzione in x. Può essere scritto Poi chiamato derivata parziale funzioni z = f(x, y) in x. Designazione: La derivata parziale di una funzione rispetto a y è definita in modo simile. senso geometrico la derivata parziale (diciamo) è la tangente della pendenza della tangente disegnata nel punto N 0 (x 0, y 0, z 0) alla sezione della superficie dal piano y \u003d y 0. Incremento completo e differenziale totale.
piano tangente Siano N e N 0 punti della superficie data. Tracciamo una retta NN 0 . Viene chiamato il piano che passa per il punto N 0 piano tangente alla superficie se l'angolo tra la secante NN 0 e questo piano tende a zero quando la distanza NN 0 tende a zero. Definizione. normale alla superficie nel punto N 0 si dice una retta passante per il punto N 0 perpendicolare al piano tangente a questa superficie. Ad un certo punto, la superficie ha un solo piano tangente o non lo ha affatto. Se la superficie è data dall'equazione z \u003d f (x, y), dove f (x, y) è una funzione derivabile nel punto M 0 (x 0, y 0), il piano tangente nel punto N 0 (x 0, y 0, ( x 0 ,y 0)) esiste e ha l'equazione: L'equazione per la normale alla superficie a questo punto è: senso geometrico del differenziale totale di una funzione di due variabili f (x, y) nel punto (x 0, y 0) è l'incremento dell'applicata (coordinata z) del piano tangente alla superficie durante il passaggio dal punto (x 0, y 0) al punto (x 0 + Dx, y 0 + Dy). Come visto, senso geometrico del differenziale totale di una funzione di due variabili è un analogo spaziale del significato geometrico del differenziale di una funzione di una variabile. Esempio. Trova le equazioni del piano tangente e normale alla superficie nel punto M(1, 1, 1). Equazione del piano tangente: Equazione normale: Calcoli approssimativi utilizzando il differenziale totale.
Il differenziale totale della funzione u è: Il valore esatto di questa espressione è 1.049275225687319176. Derivati parziali di ordini superiori. Se la funzione f(x, y) è definita in qualche dominio D, allora anche le sue derivate parziali saranno definite nello stesso dominio o parte di esso. Chiameremo queste derivate derivate parziali del primo ordine. Le derivate di queste funzioni saranno derivate parziali del secondo ordine. Continuando a differenziare le uguaglianze ottenute, otteniamo derivate parziali di ordini superiori. Si consideri la funzione y = f(x), che viene considerata sull'intervallo (a, b). Se è possibile specificare tale b-vicinanza del punto x1 appartenente all'intervallo (a, b) che per ogni x (x1, b) è soddisfatta la disuguaglianza f(x1) > f(x), allora y1 = Viene chiamato f1(x1). funzione massima y = f(x) vedi fig. Il massimo della funzione y = f(x) è indicato da max f(x). Se è possibile specificare un 6-intorno del punto x2 appartenente all'intervallo (a, b) tale che per ogni x appartenga a O(x2, 6), x non è uguale a x2, la disuguaglianza f(x2)< f(x)
, allora y2= f(x2) è chiamato il minimo della funzione y-f(x) (vedi Fig.). Un esempio per trovare il massimo, guarda il video seguente Il minimo della funzione y = f(x) è indicato con min f(x). In altre parole, il massimo o il minimo di una funzione y = f(x) chiamata il suo valore, che è maggiore (minore) di tutti gli altri valori presi in punti sufficientemente vicini a quello dato e diversi da esso. Nota 1. Massima funzionalità, determinato dalla disuguaglianza è chiamato massimo stretto; il massimo non stretto è definito dalla disuguaglianza f(x1) > = f(x2) Nota 2. avere un carattere locale (questi sono i valori più grandi e più piccoli della funzione in un quartiere sufficientemente piccolo del punto corrispondente); i minimi individuali di qualche funzione possono essere maggiori dei massimi della stessa funzione Il massimo e il minimo di una funzione sono detti estremi.
. Estremi nella ricerca per le funzioni di plottaggio latino estremo significa "estremo"
Senso. Il valore dell'argomento x, al quale si raggiunge l'estremo, è chiamato punto estremo. La condizione necessaria per un estremo è espressa dal seguente teorema. Teorema. Nel punto di estremo della funzione derivabile e della sua derivata è uguale a zero. Il teorema ha un significato geometrico semplice: la tangente al grafico di una funzione derivabile nel punto corrispondente è parallela all'asse x
o 
La funzione viene chiamata funzione antiderivativa. L'antiderivata di una funzione è determinata fino a un valore costante.
, ecco una costante arbitraria.
.
, e questa funzione è continua e l'uguaglianza 
.
dove .
. Se ricordiamo la definizione della derivata di una funzione e andiamo al limite in , otteniamo . Cioè, è una delle antiderivate della funzione y = f(x) sul segmento
. Quindi, l'insieme di tutti gli antiderivati F(x) può essere scritto come , dove Insieme aè una costante arbitraria.
, quindi, . Usiamo questo risultato per calcolare F(b): , cioè 
. Questa uguaglianza fornisce la formula dimostrabile di Newton-Leibniz .
. Usando questa notazione, la formula di Newton-Leibniz assumerà la forma .
.Rettangolare S.K. Funzione, definita parametricamente Polyarnaya SK
Calcolo dell'area delle figure piane
Calcolo della lunghezza dell'arco di una curva planare
Calcolo della superficie di rivoluzione
non è un'equazione differenziale
può essere considerato come un'approssimazione dell'equazione non lineare di un pendolo matematico 
per il caso di piccole ampiezze, quando y≈ peccato y.
dove m- massa corporea, X- la sua coordinata, F(X, t) è la forza che agisce sul corpo con la coordinata X al tempo t. La sua soluzione è la traiettoria del corpo sotto l'azione della forza specificata.
, Valori della funzione e punti massimo e minimo
Come agire in questi casi? Trova punto alto/basso
Esatto, prima la funzione aumenta, poi diminuisce: questo è il punto massimo!
Risposta: -15 
Risposta: -2 Trova il valore più grande/più piccolo di una funzione
.
.La natura locale degli estremi della funzione
Cerchiamo insieme gli estremi della funzione
esiste anche sull'intera linea dei numeri. Pertanto, in questo caso, solo quelli in cui, cioè, servono come punti critici. , donde e . Punti critici e dividere l'intero dominio della funzione in tre intervalli di monotonia: . Selezioniamo un punto di controllo in ciascuno di essi e troviamo a questo punto il segno della derivata.
. Pertanto, il suo grafico è simmetrico rispetto all'asse Ehi e lo studio può essere eseguito solo per l'intervallo.
e punti critici della funzione:
;
,
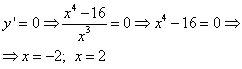e determiniamo il suo segno in : otteniamo . Poiché e , allora è il punto minimo della funzione, mentre 
.
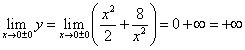
,Continuiamo a cercare insieme gli estremi della funzione
si si
A
. Il suo asintoto obliquo y = x.
.
, perché b = cost, quindi 
.
, quindi,
.
, poi 
, quindi,
.
.
.
.
(1)
.
.
Caratteristica minima
Di conseguenza, viene chiamato il massimo (minimo) della funzione massimo locale(minimo locale) in contrasto con il massimo (minimo) assoluto - il valore più grande (minimo) nel dominio della funzione.