INTEGRALE DUBLE

PRELEZA 1

Integrale duble.Definiția integralei duble și proprietățile acesteia. Integrale iterate. Reducerea integralelor duble la cele repetate. Aranjarea limitelor de integrare. Calculul integralelor duble în Sistemul cartezian coordonate.

Integrală dublă este o generalizare a conceptului integrala definita pentru cazul unei funcţii a două variabile. În acest caz, în loc de un segment de integrare, va exista un fel de cifră plată.

Lasa D este un domeniu mărginit închis și f(X y) este o funcție arbitrară definită și mărginită în acest domeniu. Vom presupune că limitele regiunii D consta dintr-un număr finit de curbe, dat de ecuaţii drăguț y=f(X) sau X=g( y), Unde f(X) Și g(y) sunt funcții continue.

Să împărțim zona D la întâmplare n părți. Zonă i al-lea segment este notat cu simbolul D s i. Pe fiecare secțiune, alegem în mod arbitrar un punct Pi,și lăsați-l să aibă coordonate într-un sistem cartezian fix ( x i ,y i). Să compunem suma integrală pentru functie f(X y) după zonă D, pentru a face acest lucru, găsim valorile funcției în toate punctele Pi, le înmulțim cu ariile segmentelor corespunzătoare Ds i si rezuma toate rezultatele:

Hai sa sunăm diam(G) zonă G cea mai mare distanță dintre punctele de limită ale acestei zone.

integrală dublă funcții f(X y) peste domeniul D se numeste limita spre care tinde sirul sumelor integrale (1.1) cu o creștere nelimitată a numărului de partiții n (în care). Aceasta este scrisă după cum urmează

Rețineți că, în general, suma integrală pentru funcţie dată iar zona de integrare dată depinde de metoda de împărțire a zonei Dși selectarea punctelor Pi. Totuși, dacă integrala dublă există, atunci aceasta înseamnă că limita sumelor integrale corespunzătoare nu mai depinde de acești factori. Pentru ca integrala dublă să existe(sau, cum se spune, astfel încât funcția f(X y) este integrabil în domeniul D), este suficient ca integrandul să fie continuuîn domeniul dat de integrare.

Lasă funcția f(X y) este integrabil în domeniu D. Deoarece limita sumelor integrale corespunzătoare pentru astfel de funcții nu depinde de metoda de partiționare a domeniului de integrare, partiționarea se poate face folosind linii verticale și orizontale. Apoi majoritatea părților din regiune D va avea o formă dreptunghiulară, aria care este egală cu D s i=D x i D y eu. Prin urmare, diferența de suprafață poate fi scrisă ca ds=dxdy. Prin urmare, în coordonate carteziene, integrale duble poate fi scris sub forma

cometariu. Dacă integrandul f(X y)º1, atunci integrala dublă va fi egală cu aria regiunii de integrare:

Rețineți că integralele duble au aceleași proprietăți ca și integralele definite. Să notăm câteva dintre ele.

Proprietățile integralelor duble.

1 0 . Proprietate liniară. Integrala sumei funcțiilor este egală cu suma integralelor:

iar factorul constant poate fi scos din semnul integral:

2 0 .Proprietate aditivă. Dacă domeniul de integrare D este împărțit în două părți, atunci integrala dublă va fi egală cu suma integralelor din fiecare parte.:

3 0 .Teorema valorii medii. Dacă funcţia f( X y)este continuă în domeniul D, atunci în acest domeniu există un astfel de punct(x,h) , ce:

Atunci apare întrebarea: cum se calculează integralele duble? Se poate calcula aproximativ, în acest scop este dezvoltat metode eficiente compilarea sumelor integrale corespunzătoare, care apoi sunt calculate numeric folosind un calculator. În calculul analitic al integralelor duble, acestea sunt reduse la două integrale definite.

Proprietățile integralelor duble.

Unele dintre proprietățile integralelor duble decurg direct din definiția acestui concept și proprietățile sumelor integrale și anume:

1. Dacă funcţia f(x, y) integrabil în D, apoi kf(x, y) este de asemenea integrabil în această regiune și (24.4)

2. Dacă se află în zonă D funcții integrabile f(x, y)Și g(x, y), apoi funcțiile f(x, y) ± g(x, y), și în care

3. Dacă pentru integrabil în domeniu D funcții f(x, y)Și g(x, y) inegalitatea f(x, y)≤g(x, y), apoi

(24.6)

Să mai demonstrăm câteva proprietăți ale integralei duble:

4. Daca zona Dîmpărțit în două zone D 1 și D 2 fără puncte interne comune și funcție f(x, y) continuu in regiune D, apoi

(24.7) Dovada . Sumă integrală asupra zonei D poate fi reprezentat ca:

unde este împărțirea zonei D trasat astfel încât granița dintre D 1 și D 2 constă din limitele unor părți ale partiției. Trecând apoi la limita de la , obținem egalitatea (24.7).

5. În cazul integrabilităţii pe D funcții f(x, y)în această regiune, funcția este de asemenea integrabilă | f(x, y) |, și inegalitatea

(24.8)

Dovada.

de unde, trecând la limita ca , obținem inegalitatea (24.8)

6. unde S D– zona regiunii D. Dovada acestei afirmații se obține prin substituirea în suma integrală f(x, y)≡ 0.

7. Dacă este integrabil în regiune D funcţie f(x, y) satisface inegalitatea

m ≤ f(x, y) ≤ M,

apoi (24.9)

Dovada.

Demonstrarea se realizează prin trecerea la limita de la inegalitatea evidentă

Consecinţă.

Dacă împărțim toate părțile inegalității (24.9) la D, putem obține așa-numita teoremă a valorii medii:

În special, sub condiția continuității funcției fîn D există un astfel de punct în această regiune ( x 0, y 0), în care f(x 0, y 0) = μ , adică

-

O altă formulare a teoremei valorii medii.

Sensul geometric al integralei duble.

Luați în considerare un corp V, mărginită de o parte a suprafeței dată de ecuație z = f(x, y), proiecție D această suprafață față de planul O huși o suprafață cilindrică laterală obținută din generatoare verticale care leagă punctele limitei suprafeței cu proiecțiile lor.

z=f(x,y)

V

y P i D Fig.2.

Vom căuta volumul acestui corp ca limită a sumei volumelor cilindrilor ale căror baze sunt părțile Δ Si zone D, iar înălțimile sunt segmente cu lungimi f(Pi), unde punctele Pi aparțin lui Δ Si. Trecând la limita la , obținem asta

(24.11)

adică integrala dublă este volumul așa-numitului cilindric delimitat de sus de suprafață z = f(x, y), iar mai jos - zona D.

Calcularea unei integrale duble prin reducerea acesteia la una iterată.

Luați în considerare zona D delimitate de linii x=a, x=b(A< b ), unde φ 1 ( X) și φ 2 ( X) sunt continue pe [ a, b]. Apoi orice linie paralelă cu axa de coordonate O la si trecand prin punctul interior al regiunii D, traversează limita regiunii în două puncte: N 1 și N 2 (Fig. 1). Să numim această zonă corect in on-

la regula axei O la. În mod similar, cel

y=φ 2 (X) există o zonă corectă în direcție

N 2 axe O X. Zona corectă în direcția

Ambii axele de coordonate, vom

D spune-i bine. De exemplu,

zona corectă este prezentată în Fig.1.

y=φ 1 (X) N 1

O a b x

Lasă funcția f(x, y) continuu in regiune D. Luați în considerare expresia

, (24.12)

numit integrală dublă din functie f(x, y) pe regiune D. Să calculăm mai întâi integrala internă (în paranteze) peste variabilă la socoteală X permanent. Rezultatul va fi functie continua din X:

Integram functia rezultata peste X variind de la dar inainte de b. Drept urmare, obținem numărul

Să demonstrăm o proprietate importantă a integralei duble.

Teorema 1. Dacă zona D, corectați în direcția O la, împărțit în două regiuni D 1 și D 2 drept, paralel cu axa O la sau axa O X, apoi integrala dublă peste regiune D va fi egală cu suma acelorași integrale peste regiuni D 1 și D 2:

Dovada.

a) Lasă linia x = c pauze D pe D 1 și D 2, corectează în direcția O la. Apoi

+

+

b) Lasă linia y=h pauze D pe cele din dreapta in directia O la zone D 1 și D 2 (Fig. 2). Notează prin M 1 (A 1 , h) Și M 2 (b 1 , h) punctele de intersecție ale dreptei y=h cu bordura L zone D.

y Regiune D 1 limitat de linii continue

y=φ 2 (X) 1) y=φ 1 (X);

D 2 2) curba DAR 1 M 1 M 2 ÎN, a cărui ecuație o scriem

h M 1 M 2 y=φ 1 *(X), Unde φ 1 *(X) = φ 2 (X) la a ≤ x ≤ a 1 și

A 1 D 1 Bb 1 ≤ x ≤ b, φ 1 *(X) = h la dar 1 ≤ x ≤ b 1 ;

3) drept x = a, x = b.

Regiune D 2 limitat de linii y=φ 1 *(X),

Ay= φ 2 (X),dar 1 ≤ x ≤ b 1 .

y=φ 1 (X) Să aplicăm integralei interioare teorema pe

împărțirea intervalului de integrare:

O a a 1 b 1 b

+

Reprezentăm a doua dintre integralele obținute ca sumă:

+ + .

În măsura în care φ 1 *(X) = φ 2 (X) la a ≤ x ≤ a 1 și b 1 ≤ x ≤ b, prima și a treia integrală obținute sunt identic egale cu zero. Prin urmare,

I D = , adică

Integrale duble pentru manechine

Această lecție prezintă subiectul extins al integralelor multiple pe care elevii le întâlnesc de obicei în al doilea an. dublu și integrale triple nu-l poți intimida pe profan mai rău decât ecuatii diferentiale, așa că ne vom ocupa imediat de întrebarea: este greu sau nu? Desigur, pentru unii va fi dificil și, să fiu sincer, am fost puțin viclean cu titlul articolului - pentru a învăța cum să rezolvi integralele duble, trebuie să ai niște abilități. În primul rând, dacă vorbim de integrale, atunci, evident, trebuie să integrăm. Logic. Prin urmare, pentru a stăpâni exemple, trebuie să puteți găsi integrale nedefinite si calculeaza integrale definite cel putin la un nivel mediu. Vestea bună este că integralele în sine sunt destul de simple în majoritatea cazurilor.

Cine trebuie să fie dur? E de înțeles. Cei care au băut multă bere în primele semestre. Totuși, voi liniști și studenții normali - site-ul are toate materialele pentru a completa golurile sau neînțelegerile. Trebuie doar să petreci mai mult timp. Link-uri către subiecte care ar trebui studiate sau revizuite vor fi incluse pe parcursul articolului.

Pe lecție introductivă Următoarele puncte de bază vor fi analizate pas cu pas și în detaliu:

– Conceptul de integrală dublă

– Zona de integrare. Ordinea de ocolire a regiunii de integrare. Cum se schimbă ordinea traversării?

După ce înțelegeți BINE toate elementele de bază, puteți trece la articol Cum se calculează integrala dublă? Exemple de soluții. În plus, există o problemă comună despre calculul integralei duble în coordonate polareși o aplicație tipică despre găsirea centrului de greutate al unei figuri mărginite plate.

Să începem cu o întrebare vitală - ce este?

Conceptul de integrală dublă

Integrală dublă în vedere generala se scrie astfel:

Înțelegem termenii și notația:
– pictograma integrală dublă;
– zona de integrare (cifră plată);
- integrantul a două variabile, adesea este destul de simplu;
- pictograme diferențiale.

Ce înseamnă să calculezi o integrală dublă?

Calcularea mediei integrale duble găsiți NUMĂR. Cel mai frecvent număr:

Și este foarte de dorit să-l găsiți corect =)

Rezultatul (numărul) poate fi negativ. Și zero, de asemenea, poate apărea cu ușurință. M-am oprit în mod special în acest moment, deoarece mulți studenți experimentează anxietate atunci când răspunsul se dovedește a fi „ceva cam ciudat”.

Mulți oameni își amintesc că „obișnuit” integrala definita este, de asemenea, un număr. Este la fel și aici. Integrala dublă are, de asemenea, un excelent sens geometric, dar mai multe despre asta mai târziu, totul are timpul lui.

Cum se calculează integrala dublă?

Pentru a calcula integrala dublă, aceasta trebuie redusă la așa-numita integrale iterate. Poate fi realizat doua feluri. Cea mai comună modalitate este:

În locul semnelor de întrebare, este necesar să se pună limitele integrării. Mai mult decât atât, semnele unice de întrebare ale integralei exterioare sunt numerele, iar semnele de întrebare duble ale integralei interioare sunt funcții o variabilă dependentă de „x”.

De unde să obții limitele integrării? Ele depind de ce zonă este dată în starea problemei. Zona este o figură plată obișnuită pe care ați întâlnit-o de multe ori, de exemplu, când calcularea ariei unei figuri plane sau calcularea volumului unui corp de revoluție. Foarte curând veți învăța cum să setați corect limitele integrării.

După efectuarea tranziției la integrale iterate, calculele urmează direct: mai întâi se ia integrala interioară și apoi cea exterioară. Unul dupa altul. De aici și numele - integrale iterate.

În linii mari, problema se reduce la calculul a două integrale definite. După cum puteți vedea, totul nu este atât de dificil și înfricoșător, iar dacă ați stăpânit integrala definită „obișnuită”, ce vă împiedică să vă ocupați de două integrale?!

A doua modalitate de trecere la integrale iterate este oarecum mai puțin comună:

Ce s-a schimbat? Ordinea integrării s-a schimbat: acum integrala internă este preluată de „x”, iar cea externă – peste „y”. Limitele integrării, indicate prin asteriscuri - va fi diferit! Stelele unice ale integralei exterioare sunt numerele, iar stelele duble ale integralei interioare sunt funcții inverseîn funcție de „y”.

Indiferent de modul în care alegem să trecem la integrale iterate, răspunsul final este sigur să fie același:

Vă rog, amintiți-vă această proprietate importantă, care poate fi folosit, printre altele, pentru a verifica soluția.

Algoritm pentru rezolvarea integralei duble:

Sistematizăm informația: în ce ordine ar trebui rezolvată problema luată în considerare?

1) Este necesar să completați desenul. Fără desen, problema nu poate fi rezolvată. Mai exact, ea decide să decidă, dar va fi ca și cum ar fi jucat șah orb. Desenul ar trebui să ilustreze zona, care este o figură plată. Cel mai adesea, figura este necomplicată și limitată la unele linii drepte, parabole, hiperbole etc. O tehnică competentă și rapidă de construire a desenelor poate fi stăpânită în lecții Grafice și proprietăți de bază ale funcțiilor elementare, Transformări grafice geometrice . Deci, primul pas este finalizarea desenului.

2) Setați limitele integrării și mergeți la integrale iterate.

3) Luați integrala interioară

4) Luați integrala exterioară și obțineți răspunsul (numărul).

Regiunea de integrare. Ordinea de ocolire a regiunii de integrare.
Cum se schimbă ordinea traversării?

În această secțiune, vom lua în considerare cea mai importantă întrebare - cum să trecem la integrale iterate și să stabilim corect limitele integrării. După cum am menționat mai sus, puteți proceda astfel:

Asa de:

În practică, această sarcină aparent simplă provoacă cele mai mari dificultăți, iar elevii devin adesea confuzi în stabilirea limitelor integrării. Luați în considerare un exemplu specific:

Exemplul 1

Soluţie: Să descriem zona de integrare în desen:

Siluetă plată obișnuită și nimic special.

Acum voi oferi fiecăruia dintre voi câte o unealtă - un băț de săpat, un indicator laser. Sarcina este de a scana fiecare punct al zonei umbrite cu un fascicul laser:

Raza laser trece prin regiunea de integrare strict de jos în sus, adică păstrezi ÎNTOTDEAUNA un pointer de mai jos figură plată. Fasciculul intră în regiune prin axa x, care este dată de ecuație, și iese din regiune printr-o parabolă (săgeată roșie). Pentru a ilumina întreaga zonă, aveți nevoie strict de la stânga la dreapta trageți indicatorul de-a lungul axei de la 0 la 1 (săgeata verde).

Deci ce s-a întâmplat:
„y” se schimbă de la 0 la ;
„x” se schimbă de la 0 la 1.

În sarcini, cele de mai sus sunt scrise sub formă de inegalități:

Aceste inegalități se numesc ocolirea domeniului de integrare sau pur și simplu ordinea integrării

După ce ne-am dat seama de ordinea traversării, putem trece de la integrală dublă la integrale iterate:

Jumătate din problemă este rezolvată. Acum trebuie să trecem la integrale iterate în al doilea mod. Pentru a face acest lucru, trebuie să găsiți funcții inverse. Cine a citit al doilea paragraf al lecției Volumul unui corp de revoluție, va fi mai usor. Ne uităm la funcțiile care stabilesc zona . Dacă este destul de simplu, atunci mergeți la funcții inverse, ceea ce înseamnă să exprimați „x” prin „y”. Singura funcție unde există și „x” și „y”, este un .

Dacă , atunci , și:
funcția inversă definește ramura dreaptă a parabolei;
funcția inversă definește ramura stângă a parabolei.

Adeseori apar îndoieli, de exemplu, funcția determină ramura stângă sau dreaptă a parabolei? Este foarte ușor să risipiți îndoielile: luați un punct al parabolei, de exemplu, (din ramura dreaptă) și înlocuiți coordonatele acesteia în orice ecuație, de exemplu, în aceeași ecuație:

Se obține egalitatea corectă, ceea ce înseamnă că funcția determină exact ramura dreaptă a parabolei, și nu stânga.

În plus, acest control(mental sau în schiță) este de dorit să se efectueze întotdeauna, după ce ați trecut la funcțiile inverse. Nu va dura nimic, dar cu siguranță te va scuti de greșeli!

Ocolim regiunea de integrare în al doilea mod:

Acum ține indicatorul laser stânga din zona de integrare. Raza laser trece prin zonă strict de la stânga la dreapta. În acest caz, intră în regiune printr-o ramură a parabolei și iese din regiune prin linia dreaptă dată de ecuație (săgeata roșie). Pentru a scana întreaga zonă cu un laser, trebuie să desenați un indicator de-a lungul axei strict de jos în sus de la 0 la 1 (săgeată verde).

În acest fel:
„x” se schimbă de la 1;
„y” se schimbă de la 0 la 1.

Ordinea de ocolire a zonei trebuie scrisă sub formă de inegalități:

Și, prin urmare, tranziția la integrale iterate este după cum urmează:

Răspuns se poate scrie astfel:

Încă o dată, vă reamintesc că rezultatul final al calculelor nu depinde de ce ordine de parcurgere a zonei am ales (de aceea punem semnul egal). Dar înainte rezultat finalîncă departe, acum sarcina noastră este doar să stabilim corect limitele integrării.

Exemplul 2

Dată o integrală dublă cu domeniul integrării . Accesați integralele iterate și setați limitele integrării în două moduri.

Acesta este un exemplu de do-it-yourself. Construiește corect un desen și urmați cu strictețe instrucțiunile(de unde și unde să străluciți cu un indicator laser). Un exemplu de atingere finală la sfârșitul lecției.

Mai des sarcină tipică apare într-o formă ușor diferită:

Exemplul 3

Construiți regiunea de integrare și

Soluţie: După condiție, este dată prima modalitate de a ocoli regiunea. Soluția începe din nou cu un desen. Aici zona nu se întinde pe un platou de argint, dar nu este greu să o construiești. În primul rând, „eliminăm” funcțiile din limitele de integrare: , . Funcția, desigur, definește o linie dreaptă, dar ce definește funcția? Să o transformăm puțin:
- un cerc cu un centru la originea coordonatelor razei 2. Funcția definește semicercul superior (nu uitați că, dacă aveți îndoieli, puteți înlocui oricând un punct situat pe semicercul superior sau inferior).

Ne uităm la limitele integralei exterioare: „x” se schimbă de la -2 la 0.

Să executăm desenul:

Pentru claritate, am indicat cu săgeți prima modalitate de a ocoli regiunea, care corespunde integralelor iterate ale condiției: .

Acum trebuie să schimbăm ordinea de ocolire a zonei, pentru aceasta vom trece la funcții inverse (să exprimăm „x” prin „y”):

Am convertit recent funcția în ecuația unui cerc, apoi exprimăm „x”:
Ca rezultat, obținem două funcții inverse:
- defineşte semicercul drept;
- definește semicercul stâng.
Din nou, dacă aveți îndoieli, luați orice punct de pe cerc și aflați care este stânga și care este dreapta.

Să schimbăm ordinea de parcurgere a zonei:

Conform celei de-a doua metode de bypass, fasciculul laser inclus spre regiune stânga prin semicercul stâng şi iesirile din dreapta peste linie (săgeata roșie). În același timp, indicatorul laser este desenat de-a lungul axei y în sus de la 0 la 2 (săgeată verde).

Astfel, ordinea de parcurgere a zonei este:

În general, se poate scrie Răspuns:

Exemplul 4

Acesta este un exemplu de do-it-yourself. Exemplul nu este foarte complicat, dar rețineți că ordinea de traversare este stabilită inițial în al doilea mod! Ce să faci în astfel de cazuri? În primul rând, există o dificultate cu desenul, deoarece desenarea unui grafic al funcției inverse este neobișnuită chiar și pentru mine. Recomand următoarea procedură: mai întâi, obținem o funcție „normală” de la (exprimăm „y” prin „x”). Apoi, construim un grafic al acestei funcții „obișnuite” (puteți construi întotdeauna cel puțin punctual). Facem același lucru cu cele mai simple funcție liniară: din exprimăm „y” și trasăm o linie dreaptă.

Analizăm limitele inițiale ale integrării: intrăm în regiune din stânga prin și ieșim prin . În același timp, toate lucrurile au loc în banda „joc” de la -1 la 0. După ce ați determinat zona de integrare pe desen, nu va fi dificil să schimbați ordinea bypass-ului. Un exemplu de soluție la sfârșitul lecției.

Un exemplu similar va fi discutat mai detaliat puțin mai târziu.

Chiar dacă înțelegi totul perfect, te rog nu te grăbi să treci direct la calculul integralei duble. Ordinea traversării este un lucru complicat și este foarte important să pun puțină mână pe această sarcină, mai ales că încă nu am acoperit totul!

În cele patru exemple precedente, zona de integrare se afla în întregime în sferturile de coordonate 1, 2, 3 și 4. Este întotdeauna așa? Nu, firesc.

Exemplul 5

Schimbați ordinea integrării

Soluţie: Să executăm desenul, în timp ce graficul funcției este de fapt o parabolă cubică, doar „se află pe o parte”:

Ordinea de traversare a regiunii care corespunde integralelor iterate , indicat prin săgeți. Vă rugăm să rețineți că în timpul execuției desenului a fost desenată o altă figură limitată (în stânga axei y). Prin urmare, ar trebui să fiți atenți atunci când determinați zona de integrare - cifra greșită poate fi confundată cu zona.

Să trecem la funcțiile inverse:
- ramura dreaptă a parabolei de care avem nevoie;

Să schimbăm ordinea de parcurgere a zonei. După cum vă amintiți, în a doua metodă de bypass, zona trebuie scanată cu un fascicul laser de la stânga la dreapta. Dar iată un lucru interesant:

Cum să acționezi în astfel de cazuri? În astfel de cazuri, ar trebui să împărțiți zona de integrare în două părți și pentru fiecare dintre părți alcătuiți integralele sale iterate:

1) Dacă „y” se schimbă de la –1 la 0 (săgeată verde), atunci raza intră în regiune printr-o parabolă cubică și iese printr-o linie dreaptă (săgeată roșie). Prin urmare, ordinea de parcurgere a zonei va fi următoarea:

2) Dacă „y” se schimbă de la 0 la 1 (săgeată maro), atunci raza intră în regiune printr-o ramură a parabolei și iese prin aceeași linie dreaptă (săgeată purpurie). Prin urmare, ordinea de parcurgere a zonei va fi următoarea:

Și integralele iterate corespunzătoare:

Integrale definite și multiple au o proprietate foarte convenabilă aditivitatea, adică se pot adăuga, ceea ce în acest caz ar trebui făcut:
- și aici este ocolirea noastră a regiunii în a doua cale sub forma sumei a două integrale.

Răspuns scrie asa:

Care este cea mai bună comandă de bypass? Desigur, cel care a fost dat în starea problemei - calculele vor fi la jumătate!

Exemplul 6

Schimbați ordinea integrării

Acesta este un exemplu de do-it-yourself. Conține semicercuri, a căror dezasamblare a fost discutată în detaliu în Exemplul 3. O mostră aproximativă de proiectare a soluției la sfârșitul lecției.

Și acum sarcina promisă, când a doua modalitate de a ocoli zona este inițial setată:

Exemplul 7

Schimbați ordinea integrării

Soluţie: Când ordinea de parcurgere este setată în al doilea mod, este recomandabil să comutați la funcțiile „normale” înainte de a desena desenul. În acest exemplu, există doi pacienți de convertit: și .
Cu o funcție liniară, totul este simplu:

Graficul funcției este o parabolă cu pretenție de canonicitate.

Să exprimăm „Y” prin „X”:

Obținem două ramuri ale parabolei: și . Pe care să o aleg? Cel mai simplu mod este să executați imediat desenul. Și chiar dacă ați uitat cu fermitate materialul geometriei analitice despre parabolă, atunci ambele ramuri pot fi încă construite punctual:

Încă o dată, aș dori să vă atrag atenția asupra faptului că acest desen Am primit mai multe figuri plate și este foarte important să alegi forma potrivită! La alegerea figurii dorite, limitele de integrare ale integralelor originale vor ajuta doar:
, și nu uitați că funcția inversă se stabilește toate parabolă.

Săgețile care indică ocolirea figurii corespund exact limitelor de integrare a integralelor .

Destul de curând veți învăța să efectuați o astfel de analiză mental și să găsiți zona dorită de integrare.

Când se găsește forma, partea finală a soluției este, în general, foarte simplă, schimbați ordinea de parcurgere a zonei:

Funcțiile inverse au fost deja găsite, iar ordinea necesară de parcurgere a regiunii este:

Răspuns:

Exemplu final de paragraf pentru auto-rezolvare:

Exemplul 8

Schimbați ordinea integrării

Soluție completăși răspunsul la sfârșitul lecției.

Începem să luăm în considerare procesul real de calcul al integralei duble și să ne familiarizăm cu semnificația ei geometrică.

Integrala dublă este numeric egală cu aria unei figuri plate (regiune de integrare). Acest cea mai simpla forma integrală dublă când funcția a două variabile este egală cu una: .

Să luăm mai întâi în considerare problema în termeni generali. Acum vei fi surprins cât de simplu este cu adevărat! Să calculăm aria unei figuri plate delimitate de linii. Pentru certitudine, presupunem că pe intervalul . Aria acestei figuri este numeric egală cu:

Să reprezentăm zona din desen:

Să alegem prima modalitate de a ocoli zona:

În acest fel:

Și imediat un truc tehnic important: integralele iterate pot fi considerate separat. Mai întâi integrala interioară, apoi integrala exterioară. Aceasta metoda Recomand cu incredere incepatorilor in tema ceainicelor.

1) Calculați integrala internă, în timp ce integrarea se realizează peste variabila „y”:

Integrală nedefinită aici este cea mai simplă, iar apoi se folosește banala formulă Newton-Leibniz, cu singura diferență că limitele integrării nu sunt numerele, ci funcțiile. În primul rând, am înlocuit limita superioară în „y” (funcția antiderivată), apoi limita inferioară

2) Rezultatul obţinut la primul paragraf trebuie înlocuit în integrala externă:

O notație mai compactă pentru întreaga soluție arată astfel:

Formula rezultată - aceasta este exact formula de lucru pentru calcularea ariei unei figuri plate folosind integrala definită „obișnuită”! Vezi lecția Calcularea ariei folosind o integrală definită, acolo este ea la fiecare pas!

adica problema calculării ariei folosind o integrală dublă putin diferit din problema găsirii zonei folosind o integrală definită ! De fapt, sunt una și aceeași!

În consecință, nu ar trebui să apară dificultăți! Nu voi lua în considerare foarte multe exemple, deoarece, de fapt, ați întâmpinat această problemă în mod repetat.

Exemplul 9

Folosind integrala dublă, calculați aria unei figuri plane delimitate de linii.

Soluţie: Să reprezentăm zona din desen:

Aria figurii se calculează folosind integrala dublă conform formulei:

Să alegem următoarea ordine de parcurgere a regiunii:

Aici și mai jos, nu voi intra în cum să traversez o zonă pentru că primul paragraf a fost foarte detaliat.

În acest fel:

După cum am observat deja, este mai bine pentru începători să calculeze integrale iterate separat, voi adera la aceeași metodă:

1) În primul rând, folosind formula Newton-Leibniz, ne ocupăm de integrala internă:

2) Rezultatul obținut la prima etapă este înlocuit în integrala exterioară:

Punctul 2 este de fapt găsirea aria unei figuri plate folosind o integrală definită.

Răspuns:

Iată o sarcină atât de stupidă și naivă.

Un exemplu curios pentru o soluție independentă:

Exemplul 10

Folosind integrala dublă, calculați aria unei figuri plate delimitate de linii , ,

Un exemplu de soluție finală la sfârșitul lecției.

În exemplele 9-10, este mult mai profitabil să folosiți prima modalitate de a ocoli zona, cititorii curioși, apropo, pot schimba ordinea ocolirii și pot calcula zonele în al doilea mod. Dacă nu greșești, atunci, firește, se obțin aceleași valori ale zonei.

Pentru o funcție a două variabile, definite ca z = f(X, y) .

Integrala dubla se scrie astfel:

Aici D- o figură plată mărginită de drepte, ale cărei expresii (egalități) sunt date în sarcina calculării integralei duble. Stânga și dreapta - egalități, în care variabila din stânga X, iar deasupra și dedesubt - prin egalități, în care variabila din stânga y. Acest loc și mai departe este unul dintre cele mai importante pentru înțelegerea tehnicii de calcul a integralei duble.

Calculați integrala dublă - înseamnă a găsi un număr egal cu aria figurii menționate D .

Până ne atingem definiții ale integralei duble , și vom învăța să o calculăm. Este mai ușor de înțeles ce este o integrală dublă atunci când au fost rezolvate mai multe probleme pentru a o calcula, așa că veți găsi definiția unei integrale duble la sfârșitul acestei lecții. Privind puțin înainte, putem doar să remarcăm că definiția integralei duble este asociată și cu figura menționată D .

Dacă cifra D este un dreptunghi, toate liniile care îl delimitează sunt drepte. Dacă cifra D- curbilinii, apoi în stânga și în dreapta este limitat de linii drepte, iar de sus și de jos - de linii curbe date de egalitățile date în sarcină. Există, de asemenea, cazuri când o cifră D- un triunghi, dar despre astfel de cazuri un pic mai departe.

Pentru a calcula integrala dublă, este deci necesar să sortăm liniile care mărginesc figura D, care are un nume strict - regiunea de integrare. Sortați în stânga și dreapta și sus și jos. Acest lucru va fi necesar când reducerea integralei duble la integrala iterata – metoda de calcul a integralei duble.

Carcasa cu suprafata dreptunghiulara:

Cazul regiunii curbilinii:

Și aceasta este deja o soluție a integralelor definite cunoscute nouă, în care sunt stabilite limitele superioare și inferioare de integrare. Expresii care definesc linii care delimitează o formă D, vor fi limitele integrării pentru integralele definite uzuale, de care ne apropiem deja.

Reducerea integralei duble la iterată

Carcasă cu zonă dreptunghiulară

Fie ca o astfel de funcție să aibă o integrală dublă

La calculați această integrală dublă , trebuie să o reduceți la integrala iterată, care are forma

.

Mai întâi trebuie să calculați integrala definită interioară (dreapta), apoi integrala definitivă exterioară (stânga).

Puteți schimba rolurile XȘi y

.

Exemplul 1 Calculați integrala dublă

Calculăm integrala interioară (dreapta), considerând y o constantă. Noi primim.

.

Exemplul 2 Calculați integrala dublă

,

Soluţie. Reducem această integrală dublă la integrala iterată

Pe desen construim zona de integrare:

Acum calculăm integrala exterioară (stânga) din integrala interioară (dreapta) tocmai calculată:

Rezultatul va fi soluția acestei integrale duble.

Calculați singur integrala dublă și apoi vedeți soluția

Cazul regiunii curbilinii sau triunghiulare

Să fie dată din nou o funcție a două variabile f(X, y) , și restricțiile pentru D: are un aspect ușor diferit:

Această intrare înseamnă că cifra D limită la stânga și la dreapta, ca în cazul unei regiuni rectilinie - linii drepte X = AȘi X = b, dar mai jos și deasupra sunt curbele care sunt date de ecuațiile și . Cu alte cuvinte, și sunt funcții.

Fie ca o astfel de funcție să aibă și o integrală dublă

Pentru a calcula această integrală dublă, trebuie să o reducem la integrala iterată, care are forma

.

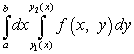Iată limitele integrării AȘi b sunt numere și și sunt funcții. În cazul unei regiuni triunghiulare, una dintre funcțiile sau este ecuația unei drepte. Acest caz va fi discutat în Exemplul 3.

Ca și în cazul unei regiuni rectilinie, mai întâi trebuie să calculați integrala definită dreaptă, apoi integrala definită stânga.

De asemenea, puteți schimba rolurile în același mod. XȘi y. Atunci integrala repetată va avea forma

.

O astfel de integrală iterată trebuie rezolvată exact în același mod: mai întâi, integrala interioară (dreapta), apoi cea exterioară (stânga).

Exemplul 5 Calculați integrala dublă

,

Soluţie. Reducem această integrală dublă la integrala iterată

.

Pe desen construim zona de integrare și vedem că este triunghiulară:

Calculăm integrala interioară (dreapta), considerând x ca o constantă. Noi primim.

Acum calculăm integrala exterioară (stânga) a integralei interioare (dreapta) tocmai calculată. În primul rând, reprezentăm această integrală ca o sumă de integrale:

.

Calculăm primul termen:

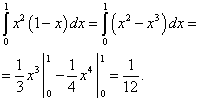
Calculăm al doilea termen:

Calculăm al treilea termen:

Obținem suma, care va fi soluția acestei integrale duble:

.

Exemplul 6 Calculați integrala dublă

Soluţie. Reducem această integrală dublă la integrala iterată

Pe desen construim zona de integrare:

Calculăm integrala interioară (dreapta), considerând x ca o constantă. Noi primim.

.

Acum calculăm integrala exterioară (stânga) din integrala interioară (dreapta) tocmai calculată:

Rezultatul va fi soluția acestei integrale duble.

X- bine si rau y-domenii corecte şi incorecte de integrare

Se întâmplă că aria de integrare a unei integrale duble este limitată de astfel de linii încât devine necesar să se împartă aria de integrare în părți și să se rezolve separat fiecare integrală iterată corespunzătoare. Acestea sunt cazurile când:

1) zona de integrare este o figură care are două sau mai multe două linii drepte sau curbe sub forma unei granițe inferioare sau superioare (stânga sau dreaptă);

2) aria de integrare este o figură a cărei graniță liniile se intersectează în mai mult de două puncte.

Dacă cele de mai sus se aplică la limita stângă sau dreaptă a regiunii de integrare, adică restricțiile date de liniile exprimate prin X, atunci se numește domeniul integrării X- gresit. Dacă o linie dreaptă y = y0 intersectează limita corespunzătoare doar într-un punct, iar dacă doar o linie sau o curbă servește drept graniță, atunci regiunea de integrare se numește X-corect

În mod similar, dacă granița definită prin linii exprimate în termeni de y, Drept X = X0 se intersectează în mai mult de un punct sau dacă mai multe linii sau curbe servesc drept graniță, atunci aria de integrare se numește y- gresit. Scoateți semnele acum y-zona potrivită, probabil, destul de simplu.

Până acum, am luat în considerare exemple de X- incorectă și y-zone regulate de integrare. Acum luați în considerare cazurile în care condiția de corectitudine este încălcată.

Exemplul 7 Calculați o integrală dublă a cărei zonă de integrare este limitată de linii y = X , X y = 1 , y = 2 .

Soluţie. Zona de integrare este y-incorect, deoarece marginea sa inferioară nu poate fi setată cu o singură linie y = y(X) . După cum puteți vedea în figura de mai sus, limita inferioară este formată din y = X(maro închis) și X y= 1 (verde). Prin urmare direct X= 1 (negru) putem împărți zona de integrare în două părți - și .

Această integrală dublă se calculează după cum urmează:

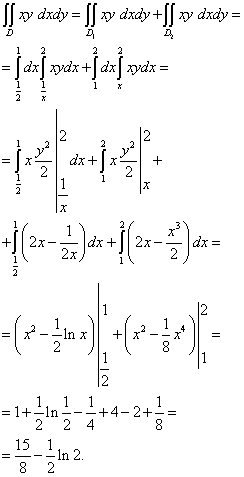
Schimbarea ordinii de integrare

După cum sa menționat mai sus, după reducerea integralei duble la integrala iterată, se pot schimba variabilele XȘi y roluri sau, cu alte cuvinte, schimbarea ordinii integrării.

Schimbarea în ordinea integrării poate fi descrisă figurativ prin următoarele cuvinte ale lui O „Henry:” Așa se comportă locuitorul junglei - fiara, care a intrat în cușcă, și așa se comportă locuitorul cuștii - un om, pierdut în jungla îndoielilor. „Rezultatul, tot după O” Henry, este unul și același: „Chalmers a rupt scrisoarea în o mie de bucăți minuscule și a început să-și chinuie covorul scump, dând-o înapoi și mai departe." ( O.Henry. Scheherazade din Madison Square.)

Atunci, dacă avem integrala stângă peste variabilă X, și cel potrivit y, apoi după schimbarea ordinii de integrare, totul va fi invers. Atunci limitele de integrare pentru „noul” y trebuie „împrumutate” de la „vechiul” x, iar limitele de integrare pentru „noul” x ar trebui obținute sub forma funcție inversă, rezolvând ecuația față de x care stabilește limita pentru y.

Exemplul 8

.

Soluţie. După schimbarea ordinii de integrare, integrala peste y devine stânga, iar integrala peste x devine dreapta. Vom împrumuta limitele de integrare pentru „noul” jucător de la „vechiul” X, adică limita inferioară este egală cu zero, iar limita superioară este egală cu unu. Limitele de integrare pentru jucătorul „vechi” sunt date de ecuațiile și . După ce am rezolvat aceste ecuații în raport cu x, obținem noi limite de integrare pentru x:

(inferioară) și (superioară).

Astfel, după schimbarea ordinii de integrare, integrala iterată se va scrie după cum urmează:

.

După schimbarea ordinii de integrare în integrala dublă, domeniul de integrare se transformă adesea în y- greșit sau X- incorect (vezi paragraful anterior). Apoi este necesar să se împartă regiunea de integrare în părți și să se rezolve separat fiecare integrală iterată corespunzătoare.

Întrucât împărțirea domeniului de integrare în părți prezintă anumite dificultăți pentru mulți studenți, nu ne vom limita la exemplul dat în paragraful anterior, ci vom analiza încă câteva exemple.

Exemplul 9 Schimbați ordinea de integrare pentru integrala iterată

.

Soluţie. Deci, aria de integrare a acestei integrale iterate este limitată de linii drepte y = 1 , y = 3 , X = 0 , X = 2y .

Când se integrează într-o ordine diferită, limita inferioară a regiunii constă din două linii drepte: ABȘi î.Hr, care sunt date de ecuații y= 1 și y = X/2 , care poate fi văzut în figura de mai jos.

Calea de ieșire dintr-o astfel de incertitudine este împărțirea domeniului de integrare în două părți. Zona de integrare va fi împărțită printr-o linie dreaptă BM. Noile limite de integrare sunt calculate prin constatare funcție inversă. Conform acestei soluții, integrala repetată după schimbarea ordinii de integrare va fi egală cu suma a două integrale:

În mod firesc, soluția integralei duble va fi aceeași, ceea ce se reduce la integrala iterată dată în condiția acestui exemplu.

Exemplul 10 Schimbați ordinea de integrare pentru integrala iterată

.

Soluţie. Deci, aria de integrare a integralei iterate este limitată de linii drepte X = 0 , X= 2 și curbele și .

După cum se poate observa în figura de mai jos, o linie dreaptă paralelă cu axa 0x, va intersecta limita inferioară a regiunii de integrare în mai mult de două puncte.

Prin urmare, împărțim domeniul de integrare în trei părți prin linii drepte, care sunt desenate cu negru în figură. Noile limite de integrare sunt calculate prin găsirea funcției inverse. Limitele pentru cele trei noi domenii de integrare vor fi următoarele.

Conform acestei soluții, integrala repetată după schimbarea ordinii de integrare va fi egală cu suma a trei integrale:

Aceeași sumă a trei integrale va fi egală cu integrala dublă, care se reduce la integrala iterată dată în condiția acestui exemplu.

Și totuși, circumstanțele de forță majoră interferează adesea cu studenții aflați deja la pasul anterior - stabilirea limitelor integrării. Anxietatea și confuzia nu sunt lipsite de o anumită bază: dacă de obicei este suficient să te uiți la desen pentru a împărți domeniul de integrare în părți și pentru a rezolva integrala iterată - tabelul integralelor, atunci este nevoie de o anumită experiență de pregătire în stabilirea limitelor integrare. Să trecem printr-un exemplu în care să ne oprim doar pe aranjarea limitelor integrării și - aproape automat - pe împărțirea regiunii și să omitem soluția în sine.

Exemplul 11. Aflați limitele de integrare a unei integrale duble dacă aria de integrare D setați după cum urmează:

y - 2X ≤ 0;
2 ani - X ≥ 0;
X y ≤ 2.

Soluţie. în mod explicit (via XȘi y„fără impurități”) nu sunt specificate liniile care limitează zona de integrare. Deoarece pentru x se dovedesc cel mai adesea a fi linii drepte care ating la un moment dat limitele superioare și inferioare exprimate prin y, atunci vom merge exact pe această cale. Mai mult, la schimbarea ordinii de integrare, obținem o zonă de integrare cu aceeași zonă. Să rezolvăm inegalitățile pentru jucător și să obținem:

y ≤ 2X;
y ≥ X/2;
y ≤ 2/X.

Construim liniile rezultate pe desen. Limitele integrării în raport cu x sunt într-adevăr liniile X= 0 și X= 2 . Dar regiunea de integrare s-a dovedit a fi y-incorect, deoarece marginea sa superioară nu poate fi setată cu o singură linie y = y(X) .

1.1 Definiția integralei duble

1.2 Proprietăți ale integralei duble

Proprietățile integralei duble (și derivarea lor) sunt similare cu proprietățile corespunzătoare ale integralei unice definite.

1°. Aditivitate. Dacă funcția f(x, y) este integrabilă în domeniul D și dacă domeniul D este împărțit de o curbă Г de zonă zero în două domenii conexe D 1 și D 2 fără puncte interioare comune, atunci funcția f(x, y) este integrabil în fiecare din regiunile D 1 şi D 2 , şi

2°. Proprietate liniară. Dacă funcțiile f(x, y) și g(x, y) sunt integrabile în domeniul D, nu? Și? - orice numere reale, apoi funcția [? f(x, y) + ? g(x, y)] este de asemenea integrabil în domeniul D, și

3°. Dacă funcțiile f(x, y) și g(x, y) sunt integrabile în domeniul D, atunci produsul acestor funcții este de asemenea integrabil în D.

4°. Dacă funcțiile f(x, y) și g(x, y) sunt ambele integrabile în domeniul D și peste tot în acest domeniu f(x, y) ? g(x, y), atunci

5°. Dacă funcția f(x, y) este integrabilă în domeniul D, atunci funcția |f(x, y)| este integrabil în domeniul D, și

(Desigur, integrabilitatea lui |f(x, y)| în D nu implică integrabilitatea lui f(x, y) în D.)

6°. Teorema valorii medii. Dacă ambele funcții f(x, y) și g(x, y) sunt integrabile într-un domeniu D, funcția g(x, y) este nenegativă (nepozitivă) peste tot în acest domeniu, M și m sunt cele mai bune limite superioare și inferioare ale funcției f( x, y) în domeniul D, atunci există un număr care satisface inegalitatea m ? ? ? M și astfel încât formula

În special, dacă funcția f(x, y) este continuă în D, iar domeniul D este conex, atunci în acest domeniu există un astfel de punct (?, ?), ce? = f(?, ?), iar formula devine

7°. Important proprietate geometrică. egală cu suprafața regiunii D

Fie dat un corp T în spațiu (Fig. 2.1), mărginit de jos de regiunea D, de sus - de graficul unei funcții continue și nenegative) z \u003d f (x, y,) care este definit în regiunea D, din laturi - printr-o suprafață cilindrică, al cărei ghid este domeniul limită D, iar generatoarele sunt paralele cu axa Oz. Un corp de acest tip se numește corp cilindric.

1.3 Interpretarea geometrică a integralei duble

1.4 Conceptul de integrală dublă pentru un dreptunghi

Fie definită o funcție arbitrară f(x, y) peste tot pe dreptunghiul R = ? (Vezi fig. 1).

Să împărțim segmentul a ? X? b în n segmente parțiale folosind punctele a = x 0< x 1 < x 2 < ... < x n = b, а сегмент c ? y ? d на p частичных сегментов при помощи точек c = y 0 < y 1 < y 2 < ... < y p = d.

Această împărțire cu ajutorul liniilor, paralel cu axele Ox și Oy, corespunde împărțirii dreptunghiului R în n · p dreptunghiuri parțiale R kl = ? (k = 1, 2, ..., n; l = 1, 2, ..., p). Partiția specificată a dreptunghiului R va fi notată prin simbolul T. În cele ce urmează, în această secțiune, termenul „dreptunghi” va însemna un dreptunghi cu laturile paralele cu axele de coordonate.

Pe fiecare dreptunghi parțial R kl, alegem un punct arbitrar (? k , ? l). Punând?x k = x k - x k-1 , ?y l = y l - y l-1 , notăm cu?R kl aria dreptunghiului R kl . Evident, ?R kl = ?x k ?y l .

se numește suma integrală a funcției f(x, y) corespunzătoare unei partiții date T a dreptunghiului R și unei alegeri date de puncte intermediare (?k, ?l) pe dreptunghiurile parțiale ale partiției T.

Diagonala se va numi diametrul dreptunghiului R kl . Un simbol? notează cel mai mare dintre diametrele tuturor dreptunghiurilor parțiale R kl .

Numărul I se numește limita sumelor integrale (1) pentru? > 0 dacă pentru orice număr pozitiv? puteți specifica acest lucru număr pozitiv?, ce la?< ? независимо от выбора точек (? k , ? l) на частичных прямоугольниках R выполняется равенство

| ? - eu |< ?.

O funcţie f(x, y) se numeşte integrabilă (după Riemann) pe un dreptunghi R dacă există o limită finită I a sumelor integrale ale acestei funcţii la? > 0.

Această limită I se numește integrală dublă a funcției f(x, y) peste dreptunghiul R și se notează cu unul dintre următoarele simboluri:

Cometariu. La fel ca și pentru integrala definită unică, se stabilește că orice funcție f(x, y) integrabilă pe dreptunghiul R este mărginită pe acest dreptunghi.

Acest lucru oferă motive de luat în considerare doar în cele ce urmează caracteristici limitate f(x, y).