De la Wikipedia, enciclopedia liberă

Infinitezimal - functie numerica sau o succesiune care tinde spre zero.

infinit de mare- o funcție numerică sau o secvență care tinde spre infinitul unui anumit semn.

Calcul infinitezimale și mari

Calcul infinitezimal- calcule efectuate cu valori infinitezimale, în care rezultatul derivat este considerat ca o sumă infinită a celor infinitezimale. Calcul infinitezimal este concept general pentru calculul diferențial și integral, care formează baza matematicii superioare moderne. Conceptul de mărime infinitezimală este strâns legat de conceptul de limită.

Infinitezimal

Urmare $un$ numit infinitezimal, dacă $\backslash lim\backslash limits\_(n\backslash to\backslash infty)a\_n=0$. De exemplu, succesiunea de numere $a\_n=\backslash dfrac(1)(n)$- infinit de mici.

Funcția este numită infinitezimal într-o vecinătate a unui punct $x\_0$, dacă $\backslash lim\backslash limits\_(x\backslash to\; x\_0)f(x)=0$.

Funcția este numită infinitezimal la infinit, dacă $\backslash lim\backslash limits\_(x\backslash to+\backslash infty)f(x)=0$ sau $\backslash lim\backslash limits\_(x\backslash to-\backslash infty)f(x)=0$.

De asemenea, infinit de mică este o funcție care este diferența dintre o funcție și limita ei, adică dacă $\backslash lim\backslash limits\_(x\backslash to+\backslash infty)f(x)=a$, apoi $f(x)-a=\backslash alpha(x)$, $\backslash lim\backslash limits\_(x\backslash to+\backslash infty)(f(x)-a)=0$.

Subliniem că o valoare infinitezimală trebuie înțeleasă ca o valoare variabilă (funcție), care este doar în proces de schimbare[când se străduiesc $X$ la $A$(din $\backslash lim\backslash limits\_(x\backslash to\; a)f(x)=0$)] este mai mic decât un număr arbitrar ( $\backslash varepsilon$). Prin urmare, de exemplu, o afirmație precum „o milioneme este o valoare infinitezimală” este incorectă: nu are sens să spunem despre un număr [valoare absolută] că este infinit de mic.

infinit de mare

În toate formulele de mai jos, infinitul la dreapta egalității implică un anumit semn (fie „plus”, fie „minus”). Aceasta este, de exemplu, funcția $x\backslash sin\; x$, nemărginit pe ambele părți, nu este infinit de mare pentru $x\backslash to+\backslash infty$.

Urmare $un$ numit infinit de mare, dacă $\backslash lim\backslash limits\_(n\backslash to\backslash infty)a\_n=\backslash infty$.

Funcția este numită infinit de mare în vecinătatea unui punct $x\_0$, dacă $\backslash lim\backslash limits\_(x\backslash to\; x\_0)f(x)=\backslash infty$.

Funcția este numită infinit de mare la infinit, dacă $\backslash lim\backslash limits\_(x\backslash to+\backslash infty)f(x)=\backslash infty$ sau $\backslash lim\backslash limits\_(x\backslash to-\backslash infty)f(x)=\backslash infty$.

Ca și în cazul infinitezimalelor, trebuie remarcat că nicio valoare unică a unei cantități infinit de mare nu poate fi numită „infinit de mare” - o cantitate infinit de mare este o funcție care numai în proces de schimbare poate fi mai mare decât un număr arbitrar.

Proprietățile infinitezimale

• Suma algebrică a unui număr finit de funcții infinit de mici este infinită funcție mică.
• Produsul infinitezimalelor este infinitezimal.
• Produsul unei secvențe infinitezimale de unul mărginit este infinitezimal. În consecință, produsul unui infinitezimal cu o constantă este infinitezimal.
• În cazul în care un $un$ este o secvență infinitezimală care păstrează semnele, atunci $b\_n=\backslash dfrac(1)(a\_n)$ este o succesiune infinit de mare.

Comparația infinitezimale

Definiții

Să presupunem că avem infinitezimale pentru același lucru $x\backslash la\; a$ cantități $\backslash alpha(x)$și $\backslash beta(x)$(sau, ceea ce nu este important pentru definiție, secvențe infinitezimale).

• În cazul în care un $\backslash lim\backslash limits\_(x\backslash to\; a)\backslash dfrac(\backslash beta)(\backslash alpha)=0$, apoi $\backslash beta$- infinit de mici ordin superior al micimii, Cum $\backslash alfa$. desemna $\backslash beta=o(\backslash alpha)$ sau $\backslash beta\backslash prec\backslash alpha$.
• În cazul în care un $\backslash lim\backslash limits\_(x\backslash to\; a)\backslash dfrac(\backslash beta)(\backslash alpha)=\backslash infty$, apoi $\backslash beta$- infinit de mici cel mai de jos ordin al micimii, Cum $\backslash alfa$. Respectiv $\backslash alpha=o(\backslash beta)$ sau $\backslash alpha\backslash prec\backslash beta$.
• În cazul în care un $\backslash lim\backslash limits\_(x\backslash to\; a)\backslash dfrac(\backslash beta)(\backslash alpha)=c$(limita este finită și nu este egală cu 0), atunci $\backslash alfa$și $\backslash beta$ sunt mărimi infinitezimale un ordin de mărime. Acesta este notat ca $\backslash alpha\backslash asymp\backslash beta$ sau ca executare simultană a relaţiilor $\backslash beta=O(\backslash alpha)$și $\backslash alpha=O(\backslash beta)$. Trebuie remarcat faptul că, în unele surse, se poate întâlni o denumire atunci când asemănarea ordinelor este scrisă sub forma unui singur raport „o mare”, care este o utilizare gratuită a acestui simbol.
• În cazul în care un $\backslash lim\backslash limits\_(x\backslash la\; a)\backslash dfrac(\backslash beta)(\backslash alpha^m)=c$(limita este finită și nu este egală cu 0), apoi mărimea infinitezimală $\backslash beta$ Are $m$-al-lea de ordinul micimii relativ infinitezimal $\backslash alfa$.

Pentru a calcula astfel de limite, este convenabil să folosiți regula lui L'Hospital.

Exemple de comparație

• La $(x\backslash la\; 0)$ magnitudinea $x^5$ Are de ordin superior micimea relativă la $x^3$, la fel de $\backslash lim\backslash limits\_(x\backslash la\; 0)\backslash dfrac(x^5)(x^3)=0$. Pe de alta parte, $x^3$ are ordinul cel mai mic de micime în raport cu $x^5$, la fel de $\backslash lim\backslash limits\_(x\backslash la\; 0)\backslash dfrac(x^3)(x^5)=\backslash infty$.

Folosind O-simbolurile rezultatelor obtinute se pot scrie sub forma urmatoare $x^5=o(x^3)$.

• $\backslash lim\backslash limits\_(x\backslash la\; 0)\backslash dfrac(2x^2+6x)(x)=\backslash lim\backslash limits\_(x\backslash to\; 0)\backslash dfrac(2x+6)(1)=\backslash lim\backslash limits\_(x\; \backslash la\; 0)(2x+6)=6,$ adică când $x\backslash la\; 0$ funcții $f(x)=2x^2+6x$și $g(x)=x$ sunt cantități infinitezimale de același ordin.

În acest caz, intrările $2x^2+6x\; =\; O(x)$și $x\; =\; O(2x^2+6x).$

• La $(x\backslash la\; 0)$ infinitezimal $2x^3$ are al treilea ordin de micime în raport cu $X$, în măsura în care $\backslash lim\backslash limits\_(x\backslash la\; 0)\backslash dfrac(2x^3)(x^3)=2$, infinitezimal $0(,)7x^2$- de ordinul doi, infinitezimal $\backslash sqrt(x)$- comanda 0,5.

Cantitati echivalente

Definiție

În cazul în care un $\backslash lim\backslash limits\_(x\backslash to\; a)\backslash dfrac(\backslash beta)(\backslash alpha)=1$, apoi cantități infinitezimale sau infinit de mari $\backslash alfa$și $\backslash beta$ numit echivalent(notat ca $\backslash alpha\backslash thicksim\backslash beta$).

În mod evident, cantitățile echivalente sunt un caz particular de cantități infinit de mici (infinit de mari) de același ordin de micime.

La $$ sunt valabile următoarele relații de echivalență (ca o consecință a așa-numitelor limite remarcabile):

• $\backslash sin\backslash alpha(x)\backslash thicksim\backslash alpha(x);$
• $\backslash mathrm(tg)\backslash ,\backslash alpha(x)\backslash thicksim\backslash alpha(x);$
• $\backslash arcsin(\backslash alpha(x))\backslash thicksim\backslash alpha(x);$
• $\backslash mathrm(arctg)\backslash ,\backslash alpha(x)\backslash thicksim\backslash alpha(x);$
• $\backslash log\_a(1+\backslash alpha(x))\backslash thicksim\backslash alpha(x)\backslash cdot\backslash frac(1)(\backslash ln(a))$, Unde $a>0$;
• $\backslash ln(1+\backslash alpha(x))\backslash thicksim\backslash alpha(x);$
• $a^(\backslash alpha(x))-1\backslash thicksim\backslash alpha(x)\backslash cdot\backslash ln(a)$, Unde $a>0$;
• $e^(\backslash alpha(x))-1\backslash thicksim\backslash alpha(x);$
• $1-\backslash cos(\backslash alpha(x))\backslash thicksim\backslash frac(\backslash alpha^2(x))(2);$
• $(1+\backslash alpha(x))^\backslash mu-1\backslash thicksim\backslash mu\backslash cdot\backslash alpha(x),\backslash quad\backslash mu\backslash in\backslash R$, deci folosiți expresia:

$\backslash sqrt[n](1+\backslash alpha(x))\backslash aprox\backslash frac(\backslash alpha(x))(n)+1$, Unde $\backslash alpha(x)\backslash xrightarrow()0$.

Teorema

Limita coeficientului (raportului) a două cantități infinitezimale sau infinit de mari nu se va modifica dacă una dintre ele (sau ambele) este înlocuită cu o valoare echivalentă.

Această teoremă este de importanță practică în găsirea limitelor (vezi exemplul).

Exemple de utilizare

• A găsi $\backslash lim\backslash limits\_(x\backslash la\; 0)\backslash dfrac(\backslash sin\; 2x)(x).$

Înlocuirea $\backslash sin\; 2x$ valoare echivalentă $2x$, primim $\backslash lim\backslash limits\_(x\backslash to\; 0)\backslash dfrac(\backslash sin\; 2x)(x)=\backslash lim\backslash limits\_(x\backslash to\; 0)\backslash dfrac(2x)(x)=2.$

• A găsi $\backslash lim\backslash limits\_(x\backslash to\backslash frac(\backslash pi)(2))\backslash dfrac(\backslash sin(4\backslash cos\; x))(\backslash cos\; x).$

La fel de $\backslash sin(4\backslash cos\; x)\backslash thicksim(4\backslash cos\; x)$ la $x\backslash la\backslash dfrac(\backslash pi)(2)$ primim $\backslash lim\backslash limits\_(x\backslash to\; \backslash frac(\backslash pi)(2))\backslash dfrac(\backslash sin(4\backslash cos\; x))(\backslash cos\; x)=\backslash lim\backslash limits\_(x\backslash to\backslash frac(\backslash pi)\; (2))\backslash dfrac(4\backslash cos\; x)(\backslash cos\; x)=4.$

• calculati $\backslash sqrt(1(,)2)$.

Folosind formula: $\backslash sqrt(1(,)2)\backslash aprox\; 1+\backslash frac(0(,)2)(2)=1(,)1$, în timp ce folosim un calculator (calcule mai precise), am obținut: $\backslash sqrt(1(,)2)\backslash aproximativ\; 1(,)095$, astfel eroarea a fost de 0,005 (sub 1%), adică metoda este utilă, datorită simplității ei, cu o estimare aproximativă a rădăcinilor aritmetice aproape de unu.

Poveste

Matematicienii vechii școli au supus conceptul infinitezimal critică dură. Michel Rolle a scris că noul calcul este „ set de greșeli strălucitoare»; Voltaire a subliniat veninos că acest calcul este arta de a calcula și măsura cu precizie lucruri a căror existență nu poate fi dovedită. Chiar și Huygens a recunoscut că nu înțelege semnificația diferențialelor de ordin superior.

Ca o ironie a sorții, se poate considera apariția la mijlocul secolului al XX-lea a analizei non-standard, care a demonstrat că punctul de vedere original - infinitezimalele propriu-zise - este și el consistent și ar putea sta la baza analizei. Odată cu apariția analizei non-standard, a devenit clar de ce matematicienii secolului al XVIII-lea, efectuând ilegal din punctul de vedere al teoria clasică acțiunile au avut însă rezultatele potrivite.

Vezi si

Scrieți o recenzie la articolul „Infinitesimal și infinit de mare”

Note

Literatură

• // Dicționar enciclopedic al lui Brockhaus și Efron: în 86 de volume (82 de volume și 4 suplimentare). - St.Petersburg. , 1890-1907.

Un fragment care caracterizează Infinitesimalul și infinitul de mare

„Ei bine, prietene, mi-e teamă că tu și călugărul îți irosești praful de pușcă”, a spus prințul Andrei batjocoritor, dar cu afecțiune.
- Ah! mon ami. [DAR! Prietenul meu.] Mă rog doar lui Dumnezeu și sper că El mă ascultă. Andre, spuse ea timid după un moment de tăcere, am o mare cerere pentru tine.
- Ce, prietene?
Nu, promite-mi că nu vei refuza. Nu te va costa nici o muncă și nu va fi nimic nedemn de tine în ea. Numai tu mă poți mângâia. Făgăduiește, Andryusha, - spuse ea, băgând mâna în geantă și ținând ceva în ea, dar încă nu se arăta, de parcă ceea ce ținea ar fi obiectul cererii și ca și cum înainte de a primi promisiunea în îndeplinirea cererii, ea nu l-a putut scoate din poșetă Este ceva.
Se uită timidă, implorând la fratele ei.
„Dacă m-ar costa mult de muncă...”, a răspuns prințul Andrei, ca și cum ar fi ghicit care era problema.
- Orice vrei, gândește-te! Știu că ești la fel ca mon pere. Gândește-te ce vrei, dar fă-o pentru mine. Fă-o te rog! Tatăl tatălui meu, bunicul nostru, l-a purtat în toate războaiele... - Tot nu a scos din poșetă ceea ce ținea. — Deci îmi promiți?
— Desigur, ce se întâmplă?
- Andre, te voi binecuvânta cu imaginea, iar tu îmi promiți că nu o vei scoate niciodată. Promisiune?
„Dacă nu-și trage gâtul până la două kilograme... Ca să-ți mulțumesc...”, a spus prințul Andrei, dar în același moment, observând expresia tulburată pe care și-a asumat-o chipul surorii sale la această glumă, s-a pocăit. „Foarte bucuros, foarte bucuros, prietene”, a adăugat el.
„Împotriva voinței tale, El te va mântui și te va îndura și te va întoarce la Sine, pentru că numai în El este adevărul și pacea”, a spus ea cu o voce tremurândă de emoție, cu un gest solemn ținându-se în ambele mâini în fața ei. frate o icoană străveche ovală a Mântuitorului cu o față neagră în casulă de argint pe un lanț de argint de măiestrie fină.
Ea și-a făcut cruce, a sărutat icoana și i-a întins-o lui Andrey.
– Te rog, Andre, pentru mine...
Din ochii ei mari străluceau raze de lumină bună și timidă. Acești ochi au luminat toată fața bolnavă și subțire și au făcut-o frumoasă. Fratele a vrut să ia scapularul, dar ea l-a oprit. Andrei a înțeles, și-a făcut cruce și a sărutat icoana. Fața lui era în același timp blândă (era atins) și batjocoritor.
- Merci, mon ami. [Multumesc prietene.]
L-a sărutat pe frunte și s-a așezat din nou pe canapea. Au tăcut.
- Așa că ți-am spus, Andre, fii bun și generos, așa cum ai fost întotdeauna. Nu o judeca pe Lise aspru, începu ea. - Este atât de dulce, atât de bună, iar poziția ei este foarte dificilă acum.
- Se pare că nu ți-am spus nimic, Masha, ca să-i reproșez soției mele ceva sau să fiu nemulțumit de ea. De ce îmi spui toate astea?
Prințesa Mary s-a înroșit pe pete și a tăcut, de parcă s-ar simți vinovată.
„Nu ți-am spus nimic, dar ți s-a spus deja. Și mă întristează.
Petele roșii au apărut și mai puternic pe fruntea, gâtul și obrajii Prințesei Marya. Ea a vrut să spună ceva și nu a putut să-l rostească. Fratele a ghicit bine: micuța prințesă a plâns după cină, a spus că a prevăzut o naștere nefericită, i-a fost frică de ei și s-a plâns de soarta ei, de socrul ei și de soțul ei. După ce a plâns, a adormit. Prințului Andrei îi era milă de sora lui.
„Să știi un lucru, Mașa, nu pot să-i reproșez, nu i-am reproșat și nu o voi reproșa niciodată soției mele pentru nimic și eu însumi nu-mi pot reproșa nimic în legătură cu ea; și așa va fi întotdeauna, în orice circumstanțe aș fi. Dar dacă vrei să afli adevărul... vrei să știi dacă sunt fericit? Nu. Este ea fericită? Nu. De ce asta? nu stiu…
Spunând acestea, s-a ridicat, s-a dus la sora lui și, aplecându-se, a sărutat-o ​​pe frunte. Ochii lui frumoși străluceau cu o strălucire inteligentă și bună, neobișnuită, dar nu se uită la sora lui, ci în întunericul ușii deschise, prin capul ei.
- Hai să mergem la ea, trebuie să ne luăm la revedere. Sau du-te singur, trezește-o și vin chiar acum. Pătrunjel! a strigat el către valet: „Vino aici, curăță-l”. E pe scaun, e pe partea dreaptă.
Prințesa Marya se ridică și se duse la ușă. Ea s-a oprit.
Andre, si tu ai. la foi, vous seriez adresse a Dieu, pour qu "il vous donne l" amour, que vous ne sentez pas et votre priere aurait ete exaucee. [Dacă ai avea credință, te-ai întoarce la Dumnezeu cu o rugăciune, pentru ca El să-ți dea dragoste pe care nu o simți și rugăciunea ta să fie ascultată.]
- Da este! – a spus prințul Andrew. - Du-te, Masha, vin imediat.
În drum spre camera surorii sale, în galeria care lega o casă de alta, prințul Andrei a întâlnit o m lle Bourienne zâmbitoare dulce, pentru a treia oară în acea zi cu un zâmbet entuziast și naiv pe care l-a întâlnit în pasaje retrase.
- Ah! je vous croyais chez vous, [Ah, am crezut că ești în camera ta,] a spus ea, roșind dintr-un motiv oarecare și coborând ochii.
Prințul Andrei o privi cu severitate. Pe chipul prințului Andrei a apărut deodată furia. Nu i-a spus nimic, ci i-a privit fruntea și părul, fără să o privească în ochi, atât de disprețuitor, încât franțuzoaica s-a înroșit și a plecat fără să spună nimic.
Când s-a apropiat de camera surorii sale, prințesa era deja trează, iar vocea ei veselă, grăbindu-se un cuvânt după altul, se auzi de la ușa deschisă. Vorbea de parcă, după o lungă perioadă de abstinență, ar fi vrut să recupereze timpul pierdut.
- Non, mais figurez vous, la vieille comtesse Zouboff avec de fausses boucles et la bouche pleine de fausses dents, comme si elle voulait defier les annees ... [Nu, imaginați-vă, bătrână contesa Zubova, cu bucle false, cu dinți falși, parcă batjocorind anii...] Xa, xa, xa, Marieie!
Exact aceeași frază despre contesa Zubova și același râs fusese deja auzit de cinci ori în fața unor străini de către prințul Andrei de la soția sa.
A intrat în liniște în cameră. Prințesa, plinuță, roșie, cu treaba în mâini, s-a așezat pe un fotoliu și a vorbit neîncetat, sortând amintirile din Petersburg și chiar frazele. Prințul Andrei a venit, a mângâiat-o pe cap și a întrebat-o dacă s-a odihnit din călătorie. Ea a răspuns și a continuat aceeași conversație.
Căruciorul stătea în șase la intrare. Afară era o noapte întunecată de toamnă. Coșerul nu a văzut bara de remorcare a trăsurii. Oamenii cu felinare se agitau pe verandă. Casa uriașă ardea cu lumini prin ferestrele ei mari. În hol se înghesuiau curţile, care voiau să-şi ia rămas bun de la tânărul prinţ; Toată gospodăria stătea în hol: Mihail Ivanovici, Mlle Bourienne, Prințesa Maria și prințesa.
Prințul Andrei a fost chemat în biroul tatălui său, care a vrut să-și ia rămas bun de la el față în față. Toată lumea îi aștepta să iasă.
Când prințul Andrei a intrat în birou, bătrânul prinț, purtând ochelari de bătrân și în haina albă, în care nu primea pe nimeni decât pe fiul său, stătea la masă și scria. S-a uitat înapoi.
- Te duci? Și a început să scrie din nou.
- Am venit să-mi iau rămas bun.
- Sărută aici, - și-a arătat obrazul, - mulțumesc, mulțumesc!
- Pentru ce-mi multumesti?
- Pentru că nu stai peste măsură, nu te ții de fusta unei femei. Serviciu mai întâi. Mulțumiri! Și a continuat să scrie, astfel încât spray-ul a zburat din pixul trosnit. - Dacă trebuie să spui ceva, spune-o. Aceste două lucruri le pot face împreună”, a adăugat el.
„Despre soția mea... îmi este atât de rușine că o las în brațele tale...”
- Ce minți? Spune ce ai nevoie.
- Când soția ta are timp să nască, trimite la Moscova după un obstetrician... Ca să fie aici.
Bătrânul prinț se opri și, de parcă n-ar fi înțeles, se uită cu ochi severi la fiul său.
„Știu că nimeni nu poate ajuta dacă natura nu ajută”, a spus prințul Andrei, aparent stânjenit. „Sunt de acord că dintr-un milion de cazuri, unul este nefericit, dar aceasta este fantezia ei și a mea. I-au spus, ea a văzut-o în vis și îi este frică.
„Hm... hm...” își spuse bătrânul prinț, continuând să termine de scris. - Eu voi.
A tăiat semnătura, s-a întors brusc spre fiul său și a râs.
- E rău, nu-i așa?
- Ce sa întâmplat, părinte?
- Soție! spuse bătrânul prinț scurt și semnificativ.
„Nu înțeleg”, a spus prințul Andrei.
„Da, nu e nimic de făcut, prietene”, a spus prințul, „toți sunt așa, nu te vei căsători.” Nu-ti fie frica; nu voi spune nimănui; si tu insuti stii.
Își apucă mâna cu mâna lui osoasă, o strânse, se uită drept la fața fiului său cu ochii lui iute, care păreau să vadă chiar prin bărbat, și râse din nou de râsul lui rece.
Fiul a oftat, mărturisind cu acest oftat că tatăl său l-a înțeles. Bătrânul, continuând să plieze și să imprime scrisori, cu viteza lui obișnuită, a apucat și a aruncat ceară de sigiliu, sigiliu și hârtie.
- Ce sa fac? Frumoasa! Voi face totul. Stai calm, spuse el scurt în timp ce tasta.
Andrei tăcea: era atât plăcut, cât și neplăcut pentru el faptul că tatăl său l-a înțeles. Bătrânul s-a ridicat și i-a întins scrisoarea fiului său.
„Ascultă”, a spus el, „nu-ți face griji pentru soția ta: ceea ce se poate face se va face”. Acum ascultă: dă scrisoarea lui Mihail Ilarionovici. Vă scriu că vă va folosi în locuri bune și nu vă va ține mult timp ca adjutant: o postare proastă! Spune-i că îmi amintesc de el și îl iubesc. Da, scrie cum te va accepta. Daca e buna, serveste. Fiul lui Nikolai Andreich Bolkonsky, din milă, nu va sluji nimănui. Ei bine, acum vino aici.
A vorbit într-un mod atât de rapid încât nu a terminat jumătate din cuvinte, dar fiul era obișnuit să-l înțeleagă. Și-a condus fiul la birou, a aruncat capacul înapoi, a scos un sertar și a scos un caiet acoperit cu scrisul lui mare, lung și concis.
„Trebuie să mor înaintea ta”. Să știți că aici sunt însemnările mele, pentru a le transfera suveranului după moartea mea. Acum, aici - iată un bilet de amanet și o scrisoare: acesta este un premiu pentru cel care scrie istoria războaielor Suvorov. Trimiteți-vă la academie. Iată observațiile mele, după ce am citit singur, vei găsi ceva util.
Andrei nu i-a spus tatălui său că probabil va trăi mult timp. Știa că nu trebuie să spună asta.
— Voi face totul, tată, spuse el.
- Ei bine, acum la revedere! Și-a lăsat fiul să-i sărute mâna și l-a îmbrățișat. „Amintește-ți un lucru, principe Andrei: dacă te ucid, îl va răni pe bătrân...” El a tăcut brusc și a continuat deodată cu voce tare: „și dacă aș afla că nu te-ai purtat ca fiul lui Nikolai Bolkonsky, îmi va fi... rușine! țipă el.
„Nu ai putut să-mi spui asta, tată”, a spus fiul zâmbind.
Bătrânul a tăcut.
„Voiam să vă întreb și eu”, a continuat prințul Andrei, „dacă mă omoară și dacă am un fiu, să nu-l lăsați să plece de la voi, așa cum v-am spus ieri, ca să crească cu voi... Vă rog.
- Nu-i dai soției tale? spuse bătrânul și râse.
Stăteau în tăcere unul față de celălalt. Ochii iute ai bătrânului erau ațintiți direct pe ochii fiului său. Ceva tremura în partea de jos a feței bătrânului prinț.
- La revedere... du-te! spuse el deodată. - Scoală-te! strigă el cu o voce furioasă și puternică, deschizând ușa biroului.
- Ce este ce? - întrebă prințesa și prințesa, văzându-l pe prințul Andrei și pentru o clipă figura unui bătrân în haină albă, fără perucă și în ochelari de bătrân, aplecându-se țipând cu voce furioasă.
Prințul Andrei a oftat și nu a răspuns.
— Ei bine, spuse el, întorcându-se către soția lui.
Și acest „bine” suna ca o batjocură rece, de parcă ar fi spus: „acum fă-ți trucurile”.
Andre, deja! [Andrey, deja!] – spuse micuța prințesă, palidând și privindu-și soțul cu frică.
A îmbrățișat-o. Ea a țipat și a căzut inconștientă pe umărul lui.
El a tras ușor înapoi umărul pe care stătea întinsă, s-a uitat în fața ei și a așezat-o cu grijă pe un scaun.
- Adio, Marieie, [La revedere, Masha,] - i-a spus el liniştit surorii sale, a sărutat-o ​​mâna în mână şi a ieşit repede din cameră.
Prințesa stătea întinsă într-un fotoliu, Mlle Bourienne își freca tâmplele. Prințesa Maria, susținându-și nora, cu ochi frumoși în lacrimi, se uita în continuare la ușa prin care a ieșit prințul Andrei, și l-a botezat. Din birou s-au auzit, ca niște împușcături, sunetele de furie adesea repetate ale bătrânului care își sufla nasul. De îndată ce prințul Andrei a plecat, ușa biroului s-a deschis repede și o siluetă severă a unui bătrân în haină albă a privit afară.
- Stânga? Foarte bine! spuse el, privind furios la micuța prințesă insensibilă, clătină din cap cu reproș și trânti ușa.

În octombrie 1805, trupele rusești au ocupat satele și orașele Arhiducatului Austriei, iar din Rusia au venit și mai multe regimente noi și, îngreunând locuitorii cu locații, au fost amplasate lângă cetatea Braunau. În Braunau era apartamentul principal al comandantului șef Kutuzov.
La 11 octombrie 1805, unul din regimentele de infanterie care tocmai sosise la Braunau, asteptand revizuirea comandantului-sef, se afla la jumatate de mile de oras. În ciuda terenului și situației non-ruse (livezi, garduri de piatră, acoperișuri de țiglă, munți vizibili în depărtare), poporul neruși, care privea soldații cu curiozitate, regimentul avea exact același aspect ca orice regiment rus care se pregătea. pentru un spectacol undeva în mijlocul Rusiei.

Unicitatea limitei și mărginirea unei secvențe numerice convergente

Definiția 1 . O secvență numerică (1) se numește mărginită dacă mulțimea de membri ai acestei secvențe formează o mulțime mărginită.

În acest caz, vom numi șirul numeric (1) valoare limitată.

Definiția 2 . Secvența numerică (1) converge și are o limită (Se poate folosi notația ) dacă .

Să repetăm ​​această definiție, folosind mai mult limba rusă. Limita unei secvențe numerice există și este egală cu un anumit număr dacă, pornind de la un anumit număr, toți membrii șirului sunt mai mici decât orice număr pozitiv dat, arbitrar mic, din acest număr limită. Același lucru se poate spune și cu alte cuvinte. Numărul va fi limita secvenței numerice (1) dacă și numai dacă pentru fiecare -vecinație a punctului toți membrii șirului, pornind de la un număr, se află în această -vecinație. Rețineți că intervalul se numește vecinătatea punctului.

Teorema 1 . Dacă există limita unei secvențe numerice, atunci aceasta este unică.

Dovada . Să demonstrăm teorema prin „metoda prin contradicție”. Să presupunem că teorema este falsă și că există cel puțin 2 numere și () pentru care sunt îndeplinite condițiile Definiției 2. În această definiție, luăm . Apoi, după număr, membrii șirului diferă de număr cu mai puțin de , iar după număr, membrii șirului diferă de număr cu mai puțin de . Să arătăm că acest lucru nu poate fi. De fapt, la relaţiile , , sunt satisfăcute, de unde pentru acestea avem . Teorema a fost demonstrată.

Teorema 2 . Dacă o secvență de numere are o limită, atunci acea secvență de numere este mărginită.

Dovada . Dovada va fi constructivă. Să luăm și să găsim cel potrivit. Să împărțim secvența în 2 părți: primii membri și membrii rămași ai secvenței. Primul grup este format dintr-un număr finit de membri și, prin urmare, este limitat. Al doilea grup este format din numere care nu se află la mai mult de 1 față de valoarea limită și, prin urmare, este, de asemenea, limitat. Unirea a două mulțimi mărginite este o mulțime mărginită. Teorema a fost demonstrată.

Cantități infinit de mici și proprietățile lor

Definiția 3 . Se numește șirul de numere infinit de mici dacă are o limită egală cu 0.

Pentru mărimile infinitezimale se folosește notația b. m.

Fie secvențe numerice și să fie date. O succesiune numerică cu un termen comun se numește suma acestora secvențe de numere. O secvență numerică cu un termen comun , se numește suma acestor secvențe numerice. O secvență numerică cu un termen comun , se numește suma acestor secvențe numerice.

Teorema 3 . Suma unui număr finit de mărimi infinitezimale este o mărime infinitezimală.

Dovada . Este suficient să dovedim afirmația pentru suma a două b. m. Fie șirurile numerice și mărimi infinitezimale, adică limitele acestor secvențe sunt egale cu 0. Acest fapt înseamnă următoarele. Dacă este dat un număr pozitiv arbitrar de mic defilare, atunci pentru număr și succesiune numerică există un număr care are proprietatea că pentru . Din același motiv, pentru același număr și șir de numere, există un număr care are proprietatea pe care o deține relația pentru . Să luăm un număr , apoi pentru . Deci, pentru un arbitrar am găsit un număr astfel încât atunci când . Prin urmare, limita șirului , este egală cu 0 și este o mărime infinitezimală. Teorema a fost demonstrată.

Teorema 4 . Produsul unei mărimi infinitezimale cu o cantitate limitată este o mărime infinitezimală.

Dovada . Fie ca șirul numeric să fie o valoare infinitezimală, iar succesiunea numerică să fie o valoare mărginită. Aceasta înseamnă că, pe de o parte, pe de altă parte, există un număr astfel încât condiția să fie îndeplinită pentru fiecare . Acum să fie dat un număr pozitiv arbitrar, cu derulare mic. Luați în considerare numărul, pentru el în șirul numeric există un număr, care are proprietatea căreia o are relația. În acest caz, condiția , ceea ce înseamnă că produsul acestor două mărimi - infinitezimal și limitat - este o mărime infinitezimală. Teorema a fost demonstrată.

Proprietăți limitate

Și cum este exact calculul limitelor, în acest caz, secvențe numerice? Încercăm să reprezentăm valoarea, a cărei limită trebuie găsită, ca sumă, diferență, produs, coeficient de cantități mai simple, a căror limită este ușor de găsit. Pentru a justifica o astfel de abordare, este necesar să se formuleze și să se dovedească proprietățile limitelor.

Teorema 5 . O secvență de numere are o limită egală cu dacă și numai dacă șirul , este o valoare infinitezimală.

Dovada . Să , adică pentru fiecare pentru , inegalitatea () este satisfăcută. Dar această inegalitate echivalează cu Pe lângă asta , adică secvența , are o limită de 0, adică, este o mărime infinitezimală. Teorema a fost demonstrată. , unde - b. m. Rezultă că . În ultima paranteză, suma a două mărimi infinitezimale este mărimea b. m. Prin urmare, este reprezentată ca o sumă și o valoare infinitezimală. În virtutea teoremei 5, aceasta înseamnă că . Se demonstrează prima afirmație a teoremei. Formulă se dovedește exact în același mod. Luați în considerare acum formula și folosiți aceeași notație pentru a transforma partea stângă. Asa de …

Este dată definiția unei secvențe infinitezimale. Are proprietățile secvențelor convergente. Există, de asemenea, proprietăți care sunt caracteristice numai pentru secvențe cu o limită egală cu zero. Sunt date dovezi ale unor astfel de proprietăți. Se are în vedere un exemplu în care este necesar să se demonstreze că succesiunea este infinitezimală.

Conţinut

Definiție

Secvență infinitezimală (αn) este o secvență convergentă a cărei limită este zero:
.

Următoarele proprietăți sunt o consecință directă a proprietăților aritmetice, aplicate unor secvențe a căror limită este zero.

Proprietatea sumei și diferenței unor secvențe infinitezimale

Sumă și diferență numărul finit de secvențe infinitezimale este o secvență infinitezimală.
De asemenea combinație liniară numărul finit de secvențe infinitezimale este o secvență infinitezimală.
Dovada limitei sumei și diferenței secvențelor numerice.

Proprietatea produsului a unor secvențe infinitezimale

Produsul unui număr finit secvențe infinitezimale este o secvență infinitezimală.
Dovada limitei produsului secvențelor numerice.

Următoarele proprietăți se aplică numai secvențelor infinitezimale și nu sunt o consecință directă a proprietăților secvențelor convergente.

( x n )
x n \u003d b + α n,
Unde (αn)

Dovezi de proprietate

Proprietatea produsului unei secvențe mărginite de un infinitezimal

Produsul unei secvențe mărginite la un infinitezimal este o succesiune infinitezimală.

Dovada

Lasă secvența să fie limitată de un număr:
(3.1) .

Fie ca șirul să fie infinitezimal. Adică, există o astfel de funcție în funcție de variabilă, încât pentru orice valoare pozitivă a variabilei, inegalitatea
(3.2) la .

Fie ca șirul să fie produsul secvențelor și . Termenul său general este:
.
Trebuie să găsim o funcție care să satisfacă inegalitatea
(3.3) la .

Aplicam (3.1) si (3.2):
.
Acest lucru se face cu . Asa de,
.
Sa punem :
.

Adică, am găsit o astfel de funcție , sub care, pentru orice număr pozitiv , următoarea inegalitate este adevărată:
(3.3) la .

Proprietatea a fost dovedită.

Proprietatea de a reprezenta o succesiune convergentă în termeni de infinitezimal

În ordinea secvenței ( x n ) are o limită b , este necesar și suficient ca
x n \u003d b + α n,
Unde (αn) este o succesiune infinitezimală.

Dovada

Nevoie. Lasa . Luați în considerare o succesiune cu un termen comun. Folosim proprietățile aritmetice ale limitelor:
.
Adică o succesiune infinitezimală.

Adecvarea. Lasa . Pe baza proprietăților aritmetice ale limitelor, avem:
.

Proprietatea a fost dovedită.

Exemplu

Toate exemplele Folosind definiția limitei unei secvențe, demonstrați că șirul

este infinit de mic.

Scriem definiția unei secvențe infinitezimale:
.
Deoarece n este un număr natural, n = 1, 2, 3, ... , apoi
,
,
.
Prin urmare, termenii șirului sunt numere pozitive. Apoi
.

Deci, am obținut următorul scor:
.
introduce numere pozitiveși :
.
Conform proprietăților inegalităților , dacă și , atunci
.

Rezultă că pentru orice pozitiv se poate găsi numar natural, deci la ,
.
Aceasta înseamnă că limita secvenței inițiale este zero și, prin urmare, este infinitezimală.

FUNCȚIILE INFINIT DE MICI ȘI PRINCIPALELE LOR PROPRIETĂȚI

Funcţie y=f(x) numit infinitezimal la x→a sau când X→∞ dacă sau , adică O funcție infinitezimală este o funcție a cărei limită într-un punct dat este zero.

Exemple.

Să stabilim următoarea relație importantă:

Teorema. Dacă funcţia y=f(x) reprezentabil la x→a ca sumă a unui număr constant bși infinit de mici α(x): f(x)=b+ α(x) apoi .

În schimb, dacă , atunci f(x)=b+α(x), Unde topor) este infinit de mic la x→a.

Dovada.

Să luăm în considerare principalele proprietăți ale funcțiilor infinitezimale.

Teorema 1. Suma algebrică a doi, trei și, în general, orice număr finit de infinitezimale este o funcție infinitezimală.

Dovada. Să dăm o dovadă pentru doi termeni. Lasa f(x)=α(x)+β(x), unde și . Trebuie să demonstrăm că pentru ε arbitrar arbitrar mic > 0 acolo δ> 0, astfel încât pt X satisfacerea inegalitatii |x – a|<δ , efectuat |f(x)|< ε.

Deci hai să reparăm număr arbitrar ε > 0. Deoarece, conform ipotezei teoremei, α(x) este o funcție infinitezimală, atunci există δ 1 > 0, care la |x – a|< δ 1 avem |α(x)|< ε / 2. La fel, din moment ce β(x) este infinitezimal, atunci există un astfel de δ 2 > 0, care la |x – a|< δ 2 avem | β(x)|< ε / 2.

Hai sa luam δ=min(δ1 , δ2 } .Apoi într-o vecinătate a punctului A rază δ fiecare dintre inegalităţi va fi satisfăcută |α(x)|< ε / 2 și | β(x)|< ε / 2. Prin urmare, în acest cartier va exista

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,

acestea. |f(x)|< ε, care trebuia demonstrat.

Teorema 2. Produsul unei funcții infinitezimale topor) pentru o funcție limitată f(x) la x→a(sau când x→∞) este o funcție infinitezimală.

Dovada. Din moment ce functia f(x) este limitat, atunci există un număr M astfel încât pentru toate valorile X dintr-o vecinătate a punctului a|f(x)|≤M.În plus, din moment ce topor) este o funcție infinitezimală pentru x→a, apoi pentru ε arbitrar > 0 există o vecinătate a punctului A, în care inegalitatea |α(x)|< ε /M. Apoi, în cel mai mic dintre aceste cartiere avem | αf|< ε /M= ε. Și asta înseamnă că af- infinit de mici. Pentru cazul x→∞ dovada se realizează în mod similar.

Din teorema demonstrată rezultă:

Consecința 1. Dacă și , atunci .

Consecința 2. Dacă c= const, atunci .

Teorema 3. Raportul unei funcții infinitezimale α(x) per functie f(x), a cărei limită este diferită de zero, este o funcție infinitezimală.

Dovada. Lasa . Apoi 1 /f(x) există o funcție limitată. Prin urmare, fracția este produsul unei funcții infinitezimale și al unei funcții mărginite, i.e. funcția este infinitezimală.

RELAȚIA DINTRE FUNCȚII INFINIT MICI ȘI INFINIT MARI

Teorema 1. Dacă funcţia f(x) este infinit de mare la x→a, apoi funcția 1 /f(x) este infinit de mic la x→a.

Dovada. Luați un număr arbitrar ε >0 și arată asta pentru unii δ>0 (în funcție de ε) pentru toate X, pentru care |x – a|<δ , inegalitatea este satisfăcută, iar asta va însemna că 1/f(x) este o funcție infinitezimală. Într-adevăr, din moment ce f(x) este o funcție infinit de mare pentru x→a, apoi există δ>0 astfel încât de îndată ce |x – a|<δ , deci | f(x)|> 1/ ε. Dar apoi pentru același lucru X.

Exemple.

Teorema inversă poate fi de asemenea demonstrată.

Teorema 2. Dacă funcţia f(x)- infinit mic la x→a(sau x→∞)și nu dispare, atunci y= 1/f(x) este o funcție infinită.

Demonstrați singur teorema.

Exemple.

Astfel, cele mai simple proprietăți ale funcțiilor infinit de mici și infinit de mari pot fi scrise folosind următoarele relații condiționate: A≠ 0

TEOREME PRIVIND LIMITE

Teorema 1. Limita sumei algebrice a două, trei și, în general, un anumit număr de funcții este egală cu suma algebrică a limitelor acestor funcții, i.e.

Dovada. Vom efectua dovada pentru doi termeni, deoarece pentru orice număr de termeni se realizează în același mod. Lasa .Apoi f(x)=b+α(x)și g(x)=c+β(x), Unde α și β sunt funcții infinitezimale. Prin urmare,

f(x) + g(x)=(b + c) + (α(x) + β(x)).

La fel de b+c este o constantă și α(x) + β(x) este o funcție infinitezimală, atunci

Exemplu. .

Teorema 2. Limita produsului a două, trei și, în general, a unui număr finit de funcții este egală cu produsul limitelor acestor funcții:

Dovada. Lasa . Prin urmare, f(x)=b+α(x)și g(x)=c+β(x)și

fg = (b + α)(c + β) = bc + (bβ + cα + αβ).

Muncă bc este o valoare constantă. Funcţie bβ + cα + αβ pe baza proprietăților funcțiilor infinitezimale, există o mărime infinitezimală. Asa de .

Consecința 1. Factorul constant poate fi scos din semnul limită:

.

Consecința 2. Limita gradului este egală cu gradul limitei:

.

Exemplu..

Teorema 3. Limita câtului a două funcții este egală cu câtul limitelor acestor funcții dacă limita numitorului este diferită de zero, i.e.

.

Dovada. Lasa . Prin urmare, f(x)=b+α(x)și g(x)=c+β(x), Unde α, β sunt infinit de mici. Luați în considerare coeficientul

O fracție este o funcție infinitezimală deoarece numărătorul este o funcție infinitezimală și numitorul are o limită c2 ≠0.

Exemple.

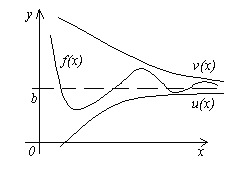
Teorema 4. Să fie date trei funcții f(x), u(x)și v(x), satisfacerea inegalităţilor u (x)≤f(x)≤v(x). Dacă funcţiile u(x)și v(x) au aceeași limită x→a(sau x→∞), apoi funcția f(x) tinde spre aceeași limită, adică dacă

, apoi .

Sensul acestei teoreme este clar din figură.

Dovada teoremei 4 poate fi găsită, de exemplu, în manualul: Piskunov N. S. Calcul diferențial și integral, vol. 1 - M .: Nauka, 1985.

Teorema 5. Eu gras x→a(sau x→∞) funcție y=f(x) ia valori nenegative y≥0și tinde spre limită b, atunci această limită nu poate fi negativă: b≥0.

Dovada. Dovada se va face prin contradictie. Să ne prefacem că b<0 , apoi |y – b|≥|b|și, prin urmare, modulul diferenței nu tinde spre zero la x→a. Dar apoi y nu merge la limita b la x→a, ceea ce contrazice condiția teoremei.

Teorema 6. Dacă două funcţii f(x)și g(x) pentru toate valorile argumentului X satisface inegalitatea f(x)≥ g(x)și avem limite, atunci avem inegalitatea b≥c.

Dovada. Conform teoremei f(x)-g(x) ≥0, prin urmare, prin teorema 5 , sau .

LIMITE UNIVERSALE

Până acum, am luat în considerare definiția limitei unei funcții când x→aîn mod arbitrar, adică limita funcției nu depindea de modul în care X către A, la stânga sau la dreapta A. Cu toate acestea, este destul de comun să găsiți funcții care nu au nicio limită în această condiție, dar au o limită dacă x→a, rămânând pe o parte a A, stânga sau dreapta (vezi fig.). Prin urmare, este introdus conceptul de limite unilaterale.

În cazul în care un f(x) tinde spre limită b la X străduindu-se pentru un număr A asa de X ia doar valori mai mici decât A, apoi scrieți și sunați blimita funcției f(x) în punctul a din stânga.