subiect :

Ţintă : Pentru a-și forma o idee despre derivatele inversului funcții trigonometrice.

Sarcini:

1. învață să găsești derivate ale acestor funcții,de a lucra cu elevii capacitatea de a diferenţia aceste funcţii folosind
munca independentă și verificarea reciprocă;

2. dezvoltarea interesului pentru matematică, calcul și cognitive aptitudini,
capacitatea de a analiza greșelile altor elevi;

3. hrănește atenția, independența

1. Moment organizatoric
Salut elevii, îi prezint regulile de lucru în lecție, explic cum să completezi corect fișa de calificare
2. Etapa motivațională
Elevii citesc ceea ce trebuie să știe și să poată face pe această temă.
Înainte de a începe, citiți regula ȚINE ȚINE.
3. Etapa operațională
Elevii completează fișa de lucru (anexată)
4.Rezumatul lecției
Reflecţie.

Astăzi la clasă:

Am aflat…

A fost interesant…

A fost dificil…

Am reușit…

Voi încerca…

FIȘĂ DE ÎNVĂȚARE

pe această temă: Derivate ale funcțiilor trigonometrice și trigonometrice inverse.

2 lecții.

CA REZULTATE ALE STUDIULUI TEMEI ESTE NECESAR

ȘTII: formule de diferențiere pentru funcții trigonometrice și trigonometrice inverse.

A FI CAPABIL SĂ: găsiți derivate ale funcțiilor trigonometrice și trigonometrice inverse.

tine minte , că algoritmul trebuie să funcționeze.

Nu uitați să treceți testul, să faceți notițe în margini, să completați fișa de calificare a subiectului.

Vă rugăm să nu lăsați întrebări la care ați avut fără răspuns.

Fii obiectiv în timpul evaluării inter pares, aceasta te va ajuta atât pe tine, cât și pe persoana pe care o verifici.

ÎȚI DORESC SUCCES!

Z ADANIE №1

Citiți și învățați formulele de diferențiere a funcțiilor trigonometrice inverse: (2 p.)

Dacă funcția este complexă, atunci

Unde z – funcția elementară

Luați în considerare exemple:

y=arcsin(x) apoi y/=

y = arcctg(3x 2 -4) atunci

y/=

Găsiți derivate:(3 p.)

y= arcsin(-x) y= arctg(-x) y= arcos(2x)

P DU-TE VERIFICA №1

Z ADANIE №2

Rezolvați oricare dintre exemplele: (3b)

dar ) y = arcos(5x - 3)

b ) y = arcctg(7x+1)

P DU-TE VERIFICA №2

Z ADANIE №3

a) Luați în considerare din nou soluția exemplului:

b) Găsiți derivate ale funcțiilor (4 p.)

arcsin(2x 2 - 5x)

arccos(4x 2 - 6x)

P DU-TE VERIFICA №3

Z ADANIE №4

Bine făcut! Tu poți să începilucrare de verificare numarul 1.

SARCINA #5

a) Luați în considerare soluția exemplului:

b) Găsiți derivate ale funcțiilor (6 p.)

P DU-TE VERIFICA №5

Bine făcut! Tu poți să începilucrare de verificare numarul 2.

LUCRARE DE VERIFICARE №1

Efectuați una dintre opțiuni (11b)

1v 2v

1. Găsiți derivate următoarele funcții:

a) 2 puncte

y = arctg(-2x) y = arccos(3x)

b) 4 puncte

y = arcos(3x 2 - 2) y = arcctg(2x 3 +1)

c) 5 puncte

y = arcsin(x 2 - 5x) + tan (2x+1) y = arccos(3x 2 - 2x) + ctg(x+4) max

puncte

primit

Scor

care

verificat

nota

2 b

3 b

1 1 b

6 b

1 4 b

total

43 b

TOTAL 43 de puncte

"5" - 33 - 43 puncte;

"4" - 24 - 32 puncte;

"3" - 18 - 23 de puncte.

Iată un tabel rezumativ pentru comoditate și claritate atunci când studiați subiectul.

Constanty=C

Funcția de putere y = x p

(x p)" = p x p - 1

Functie exponentialay = x

(a x)" = a x ln a

În special, cânda = eavem y = e x

(e x)" = e x

funcţie logaritmică

(log a x) " = 1 x ln a

În special, cânda = eavem y = log x

(ln x)" = 1 x

Funcții trigonometrice

(sin x) "= cos x (cos x)" = - sin x (t g x) " = 1 cos 2 x (c t g x)" = - 1 sin 2 x

Funcții trigonometrice inverse

(a r c sin x) " = 1 1 - x 2 (a r c cos x) " = - 1 1 - x 2 (a r c t g x) " = 1 1 + x 2 (a r c c t g x) " = - 1 1 + x 2

Funcții hiperbolice

(s h x) " = c h x (c h x) " = s h x (t h x) " = 1 c h 2 x (c t h x) " = - 1 s h 2 x

Să analizăm modul în care s-au obținut formulele din tabelul indicat sau, cu alte cuvinte, vom demonstra derivarea formulelor pentru derivate pentru fiecare tip de funcție.

Derivată a unei constante

Dovada 1

Pentru a deriva această formulă, luăm ca bază definiția derivatei unei funcții într-un punct. Folosim x 0 = x, unde X ia valoarea oricărui număr real sau, cu alte cuvinte, X este orice număr din domeniul funcției f (x) = C . Să scriem limita raportului dintre incrementul funcției și incrementul argumentului ca ∆ x → 0:

lim ∆ x → 0 ∆ f (x) ∆ x = lim ∆ x → 0 C - C ∆ x = lim ∆ x → 0 0 ∆ x = 0

Vă rugăm să rețineți că expresia 0 ∆ x se încadrează sub semnul limită. Nu este nedeterminarea lui „zero împărțit la zero”, deoarece numărătorul nu conține infinit valoare mică, și anume zero. Cu alte cuvinte, incrementul unei funcții constante este întotdeauna zero.

Deci, derivata funcției constante f (x) = C este egală cu zero pe întregul domeniu de definiție.

Exemplul 1

Date funcții constante:

f 1 (x) = 3 , f 2 (x) = a , a ∈ R , f 3 (x) = 4 . 13 7 22 , f 4 (x) = 0 , f 5 (x) = - 8 7

Soluţie

Să descriem condițiile date. În prima funcție vedem derivata numărului natural 3 . În exemplul următor, trebuie să luați derivata lui dar, Unde dar- orice numar real. Al treilea exemplu ne oferă derivata număr irațional 4 . 13 7 22 , al patrulea - derivata lui zero (zero este un număr întreg). În cele din urmă, în al cincilea caz, avem derivata fracției raționale - 8 7 .

Răspuns: derivate setați funcții este zero pentru orice real X(pe întregul domeniu de definiție)

f 1 " (x) = (3) " = 0 , f 2 " (x) = (a) " = 0 , a ∈ R , f 3 " (x) = 4 . 13 7 22 " = 0 , f 4 " (x) = 0 " = 0 , f 5 " (x) = - 8 7 " = 0

Derivata functiei de putere

Să trecem la functie de putereși formula derivatei sale, care are forma: (x p) " = p x p - 1, unde exponentul p este orice număr real.

Dovada 2

Prezentăm dovada formulei când exponentul este numar natural: p = 1, 2, 3, …

Din nou, ne bazăm pe definiția unei derivate. Să scriem limita raportului dintre incrementul funcției de putere și incrementul argumentului:

(x p) " = lim ∆ x → 0 = ∆ (x p) ∆ x = lim ∆ x → 0 (x + ∆ x) p - x p ∆ x

Pentru a simplifica expresia în numărător, folosim formula binomială a lui Newton:

(x + ∆ x) p - x p = C p 0 + x p + C p 1 x p - 1 ∆ x + C p 2 x p - 2 (∆ x) 2 + . . . + + C pp - 1 x (∆ x) p - 1 + C pp (∆ x) p - xp = = C p 1 xp - 1 ∆ x + C p 2 xp - 2 (∆ x) 2 + . . . + C p p - 1 x (∆ x) p - 1 + C p p (∆ x) p

În acest fel:

(xp) " = lim ∆ x → 0 ∆ (xp) ∆ x = lim ∆ x → 0 (x + ∆ x) p - xp ∆ x = = lim ∆ x → 0 (C p 1 xp - 1 ∆ x + C p 2 xp - 2 (∆ x) 2 + . . . + C pp - 1 x (∆ x) p - 1 + C pp (∆ x) p) ∆ x = = lim ∆ x → 0 (C p 1 xp - 1 + C p 2 xp - 2 ∆ x +... + C pp - 1 x (∆ x) p - 2 + C pp (∆ x) p - 1) = = C p 1 xp - 1 + 0 + 0 +... + 0 = p! 1! (p - 1)! xp - 1 = p xp - 1

Deci, am demonstrat formula pentru derivata unei funcții de putere atunci când exponentul este un număr natural.

Dovada 3

A da dovezi pentru cazul când p- orice număr real, altul decât zero, folosim derivata logaritmică (aici ar trebui să înțelegem diferența față de derivata funcției logaritmice). Pentru a avea o înțelegere mai completă, este de dorit să se studieze derivata funcției logaritmice și să se ocupe suplimentar de derivata unei funcții implicite date și derivata functie complexa.

Luați în considerare două cazuri: când X pozitiv și când X sunt negative.

Deci x > 0 . Atunci: x p > 0 . Luăm logaritmul egalității y \u003d x p la baza e și aplicăm proprietatea logaritmului:

y = x p ln y = ln x p ln y = p ln x

În această etapă s-a obţinut o funcţie implicit definită. Să definim derivata sa:

(ln y) " = (p ln x) 1 y y " = p 1 x ⇒ y " = p y x = p x p x = p x p - 1

Acum luăm în considerare cazul când X- un număr negativ.

Dacă indicatorul p este un număr par, atunci funcția de putere este definită și pentru x< 0 , причем является четной: y (x) = - y ((- x) p) " = - p · (- x) p - 1 · (- x) " = = p · (- x) p - 1 = p · x p - 1

Apoi xp< 0 и возможно составить доказательство, используя логарифмическую производную.

Dacă p este un număr impar, atunci funcția de putere este definită pentru x< 0 , причем является нечетной: y (x) = - y (- x) = - (- x) p . Тогда x p < 0 , а значит логарифмическую производную задействовать нельзя. В такой ситуации возможно взять за основу доказательства правила дифференцирования и правило нахождения производной сложной функции:

y "(x) \u003d (- (- x) p) " \u003d - ((- x) p) " \u003d - p (- x) p - 1 (- x) " = \u003d p (- x) ) p - 1 = p xp - 1

Ultima tranziție este posibilă pentru că dacă p este un număr impar, atunci p - 1 fie un număr par, fie zero (pentru p = 1), prin urmare, pentru negativ X egalitatea (- x) p - 1 = x p - 1 este adevărată.

Deci, am demonstrat formula pentru derivata unei funcții putere pentru orice p real.

Exemplul 2

Funcții date:

f 1 (x) = 1 x 2 3 , f 2 (x) = x 2 - 1 4 , f 3 (x) = 1 x log 7 12

Determinați derivatele lor.

Soluţie

Transformăm o parte din funcțiile date într-o formă tabelară y = x p , pe baza proprietăților gradului, apoi folosim formula:

f 1 (x) \u003d 1 x 2 3 \u003d x - 2 3 ⇒ f 1 "(x) \u003d - 2 3 x - 2 3 - 1 \u003d - 2 3 x - 5 3 f 2 "(x) \u003d x 2 - 1 4 = 2 - 1 4 x 2 - 1 4 - 1 = 2 - 1 4 x 2 - 5 4 f 3 (x) = 1 x log 7 12 = x - log 7 12 ⇒ f 3 " ( x) = - log 7 12 x - log 7 12 - 1 = - log 7 12 x - log 7 12 - log 7 7 = - log 7 12 x - log 7 84

Derivată a funcției exponențiale

Dovada 4

Deducem formula pentru derivată, pe baza definiției:

(ax) " = lim ∆ x → 0 ax + ∆ x - ax ∆ x = lim ∆ x → 0 ax (a ∆ x - 1) ∆ x = ax lim ∆ x → 0 a ∆ x - 1 ∆ x = 0 0

Avem incertitudine. Pentru a o extinde, scriem o nouă variabilă z = a ∆ x - 1 (z → 0 ca ∆ x → 0). În acest caz a ∆ x = z + 1 ⇒ ∆ x = log a (z + 1) = ln (z + 1) ln a . Pentru ultima tranziție se folosește formula pentru trecerea la o nouă bază a logaritmului.

Să efectuăm o înlocuire în limita inițială:

(ax) " = ax lim ∆ x → 0 a ∆ x - 1 ∆ x = ax ln a lim ∆ x → 0 1 1 z ln (z + 1) = ax ln a lim ∆ x → 0 1 ln (z + 1) 1 z = ax ln a 1 ln lim ∆ x → 0 (z + 1) 1 z

Reamintim a doua limită remarcabilă și apoi obținem formula pentru derivată functie exponentiala:

(a x) " = a x ln a 1 ln lim z → 0 (z + 1) 1 z = a x ln a 1 ln e = a x ln a

Exemplul 3

Funcțiile exponențiale sunt date:

f 1 (x) = 2 3 x , f 2 (x) = 5 3 x , f 3 (x) = 1 (e) x

Trebuie să găsim derivatele lor.

Soluţie

Folosim formula pentru derivata funcției exponențiale și proprietățile logaritmului:

f 1 "(x) = 2 3 x" = 2 3 x ln 2 3 = 2 3 x (ln 2 - ln 3) f 2 "(x) = 5 3 x" = 5 3 x ln 5 1 3 = 1 3 5 3 x ln 5 f 3 "(x) = 1 (e) x" = 1 ex "= 1 ex ln 1 e = 1 ex ln e - 1 = - 1 ex

Derivată a unei funcții logaritmice

Dovada 5

Prezentăm demonstrația formulei pentru derivata funcției logaritmice pentru oricare Xîn domeniul definiției și orice valori valide ale bazei a a logaritmului. Pe baza definiției derivatei, obținem:

(log ax) " = lim ∆ x → 0 log a (x + ∆ x) - log ax ∆ x = lim ∆ x → 0 log ax + ∆ xx ∆ x = = lim ∆ x → 0 1 ∆ x log a 1 + ∆ xx = lim ∆ x → 0 log a 1 + ∆ xx 1 ∆ x = = lim ∆ x → 0 log a 1 + ∆ xx 1 ∆ x xx = lim ∆ x → 0 1 x log a 1 + ∆ xxx ∆ x = = 1 x log a lim ∆ x → 0 1 + ∆ xxx ∆ x = 1 x log ae = 1 x ln e ln a = 1 x ln a

Din lanțul de egalități specificat se poate observa că transformările au fost construite pe baza proprietății logaritmului. Egalitatea lim ∆ x → 0 1 + ∆ x x x ∆ x = e este adevărată în conformitate cu a doua limită remarcabilă.

Exemplul 4

Funcțiile logaritmice sunt date:

f 1 (x) = log log 3 x , f 2 (x) = log x

Este necesar să se calculeze derivatele lor.

Soluţie

Să aplicăm formula derivată:

f 1 "(x) = (log ln 3 x)" = 1 x ln (ln 3) ; f 2 "(x) \u003d (ln x)" \u003d 1 x ln e \u003d 1 x

Deci derivata logaritmului natural este una împărțită la X.

Derivate ale funcţiilor trigonometrice

Dovada 6

Noi folosim câteva formule trigonometriceși prima limită remarcabilă pentru a deriva formula pentru derivata unei funcții trigonometrice.

Conform definiției derivatei funcției sinus, obținem:

(sin x) " = lim ∆ x → 0 sin (x + ∆ x) - sin x ∆ x

Formula pentru diferența de sinusuri ne va permite să efectuăm următoarele acțiuni:

(sin x) " = lim ∆ x → 0 sin (x + ∆ x) - sin x ∆ x = = lim ∆ x → 0 2 sin x + ∆ x - x 2 cos x + ∆ x + x 2 ∆ x = = lim ∆ x → 0 sin ∆ x 2 cos x + ∆ x 2 ∆ x 2 = = cos x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2

În cele din urmă, folosim prima limită minunată:

sin "x = cos x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = cos x

Deci derivata funcției sin x voi cos x.

De asemenea, vom demonstra formula pentru derivata cosinus în același mod:

cos "x = lim ∆ x → 0 cos (x + ∆ x) - cos x ∆ x = = lim ∆ x → 0 - 2 sin x + ∆ x - x 2 sin x + ∆ x + x 2 ∆ x = = - lim ∆ x → 0 sin ∆ x 2 sin x + ∆ x 2 ∆ x 2 = = - sin x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = - sin x

Acestea. derivata functiei cos x va fi – sin x.

Obținem formulele pentru derivatele tangentei și cotangentei pe baza regulilor de diferențiere:

tg "x = sin x cos x" = sin "x cos x - sin x cos" x cos 2 x = = cos x cos x - sin x (- sin x) cos 2 x = sin 2 x + cos 2 x cos 2 x = 1 cos 2 xctg "x = cos x sin x" = cos "x sin x - cos x sin" x sin 2 x = = - sin x sin x - cos x cos x sin 2 x = - sin 2 x + cos 2 x sin 2 x = - 1 sin 2 x

Derivate ale funcţiilor trigonometrice inverse

Secțiunea derivată funcții inverse oferă informații cuprinzătoare despre demonstrarea formulelor pentru derivatele arcsinus, arccosinus, arctangent și arccotangent, așa că nu vom duplica materialul aici.

Derivate ale funcțiilor hiperbolice

Dovada 7

Putem deriva formule pentru derivatele sinusului hiperbolic, cosinusului, tangentei și cotangentei folosind regula de diferențiere și formula pentru derivata funcției exponențiale:

sh "x = ex - e - x 2" = 1 2 ex " - e - x " == 1 2 ex - - e - x = ex + e - x 2 = chxch " x = ex + e - x 2 " = 1 2 ex "+e - x" == 1 2 ex + - e - x = ex - e - x 2 = shxth "x = shxchx" = sh "x chx - shx ch" xch 2 x = ch 2 x - sh 2 xch 2 x = 1 ch 2 xcth "x = chxshx" = ch "x shx - chx sh" xsh 2 x = sh 2 x - ch 2 xsh 2 x = - 1 sh 2 x

Dacă observați o greșeală în text, vă rugăm să o evidențiați și să apăsați Ctrl+Enter

Pentru găsire derivata unei functii trigonometrice nevoie de utilizare tabel de derivate, și anume derivatele 6-13.

Când a fost găsit derivate ale funcţiilor trigonometrice simple Pentru a evita greșelile comune, acordați atenție următoarelor puncte:

într-o expresie de funcție, unul dintre termeni este adesea sinus, cosinus sau altă funcție trigonometrică nu din argumentul functiei, ci din numarul (constantei), deci derivata acestui termen este egala cu zero;
aproape întotdeauna trebuie să simplificați expresia obținută ca urmare a diferențierii, iar pentru aceasta trebuie să folosiți cu încredere cunoștințele operațiilor cu fracții;
pentru a simplifica expresia, aproape întotdeauna trebuie să cunoaștem identitățile trigonometrice, cum ar fi formula unghiului dublu și formula unității ca sumă a pătratelor sinusului și cosinusului.

Exemplul 1 Aflați derivata unei funcții

Soluţie. Să zicem cu derivat de cosinus totul este clar, vor spune mulți care încep să studieze derivatele. Ce zici cu derivat sinus doisprezece împărțit la pi? Răspuns: considerați egal cu zero! Aici sinusul (o funcție până la urmă!) este o capcană, deoarece argumentul nu este variabila x sau orice altă variabilă, ci doar un număr. Adică, sinusul acestui număr este, de asemenea, un număr. Și derivata unui număr (constante), așa cum știm din tabelul derivatelor, este egală cu zero. Deci, lăsăm doar sinusul minus al lui x și găsim derivata acestuia, fără a uita semnul:

Exemplul 2 Aflați derivata unei funcții

Soluţie. Al doilea termen este același caz ca primul termen din exemplul anterior. Adică un număr, iar derivata numărului este zero. Găsim derivata celui de-al doilea termen ca derivată a coeficientului:

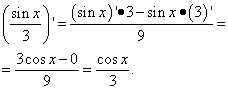
Exemplul 3 Aflați derivata unei funcții

Soluţie. Aceasta este o sarcină diferită: aici în primul termen nu există nici un arcsinus, nici o altă funcție trigonometrică, dar există x, ceea ce înseamnă că aceasta este o funcție a lui x. Prin urmare, îl diferențiem ca termen în suma funcțiilor:

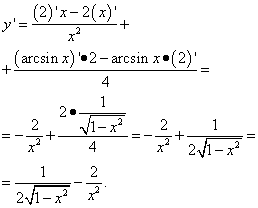
Aici s-au cerut abilități în acțiuni cu fracții, și anume în eliminarea fracției cu trei etaje.

Exemplul 4 Aflați derivata unei funcții

Soluţie. Aici litera „fi” joacă același rol ca „x” în cazurile anterioare (și în majoritatea celorlalte, dar nu în toate) - o variabilă independentă. Prin urmare, atunci când căutăm derivata produsului de funcții, nu ne vom grăbi să declarăm derivata rădăcinii lui „phi” egală cu zero. Asa de:

Dar soluția nu se termină aici. Deoarece membrii similari sunt adunați în două paranteze, mai trebuie să transformăm (simplificam) expresia. Prin urmare, înmulțim parantezele cu factorii scoși din ele, apoi reducem termenii la un numitor comun și efectuăm alte transformări elementare:

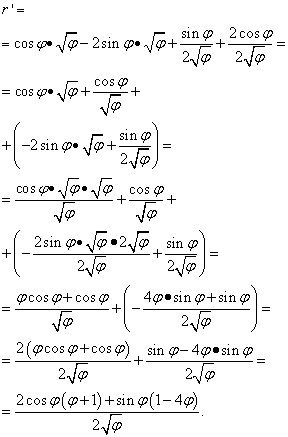
Exemplul 5 Aflați derivata unei funcții

Soluţie. În acest exemplu, va trebui să cunoaștem faptul că există o astfel de funcție trigonometrică - secanta - și formulele ei în termeni de cosinus. Diferențierea:

Exemplul 6 Aflați derivata unei funcții

Soluţie. În acest exemplu, va trebui să ne amintim formula unghiului dublu din cursul școlar. Dar mai întâi, să facem diferența:

(aceasta este formula unghiului dublu)

Calcul diferenţial al unei funcţii a unei variabile

1. Introducere

Analiza matematică- o ramură a matematicii care a luat contur în secolul al XVIII-lea și cuprinde două părți principale: calculul diferențial și integral. Derivata unei funcții este unul dintre conceptele matematice de bază calcul diferenţial. Analiza a apărut datorită eforturilor multor matematicieni (în primul rând, I. Newton și G. Leibniz) și a jucat un rol imens în dezvoltarea științelor naturii - o metodă puternică, destul de universală pentru studierea funcțiilor care apar la rezolvarea diferitelor probleme aplicate. a aparut.

2. Funcția numerică. Schema de studiu a funcției.

(Consultați notele despre subiectul „Funcția de alimentare”)

1) Domeniul de aplicare a funcției.

2) Set de valori ale funcției.

3) Funcții pare, impare.

4) Monotonitatea funcției.

5) Reversibilitatea funcției.

6) Zerourile funcției.

7) Intervale de constanță a semnului unei funcții.

8) Funcție limitată.

Exerciții:

Găsiți domeniul de aplicare al unei funcții:

dar) ; b) ; în) .

dar) ; b) ; G).

3. Conceptul de limită a unei funcții într-un punct.

Luați în considerare graficele unor funcții. Să studiem comportamentul funcțiilor în apropierea punctului x 0 , adică într-o zonă oarecare a punctului x 0 .

Orez. 1. Fig. 2. Fig. 3.

Funcția are o proprietate care o deosebește de celelalte două funcții.

1. La abordarea argumentului X la x 0în stânga și în dreapta, valorile corespunzătoare ale funcției sunt în mod arbitrar apropiate de același număr DAR.

Celelalte două funcții nu au această proprietate.

2. La abordarea argumentului X la x 0în stânga, valorile corespunzătoare ale funcției sunt în mod arbitrar apropiate de număr DAR, iar la abordarea argumentului X la x 0în dreapta, valorile corespunzătoare ale funcției sunt în mod arbitrar apropiate de număr ÎN.

3. Funcție la abordarea unui argument X la x 0 stânga și dreapta capătă valori diferite.

Ieșire: Dacă la abordarea argumentului X la x 0 în stânga și în dreapta, punctele cu coordonate sunt în mod arbitrar apropiate de punctul cu coordonate , apoi .

Exemplu: Face funcția limită în punctele x 1, x 2, x 3, x 4, x 5?

Răspuns: Funcție are o limită în punctele x 1 , x 3 ;

funcţie nu are limită în punctele x 2 , x 4 , x 5 .

cometariu:

4. Definirea unei funcții continue într-un punct și pe un interval

Conceptul de continuitate a unei funcții este asociat în mod convenabil cu ideea graficului acestei funcții ca o linie „continuă” (solidă). O linie continuă este o linie trasată fără a ridica creionul de pe hârtie.

Întrebare: Care dintre aceste funcții sunt continue?

Orez. 1. Fig. 2. Fig. 3.

Orez. 4. Fig. cinci.

Răspuns: Dintre aceste funcții, funcția prezentată în Fig. 1 este continuă. Nr. 3, deoarece graficul ei este o linie „continuă” (solidă).

Întrebare: Care sunt proprietățile funcției prezentate în Fig. Nr. 3, și nu au alte funcții?

Răspuns:

1. Funcția este definită în punctul x 0. Această proprietate nu este valabilă pentru funcția prezentată în fig. Numarul 1.

2. Există o limită finită a funcției în punctul x 0. Această proprietate nu este valabilă pentru funcțiile prezentate în fig. nr. 2, 5.

3. Limita funcției în punctul x 0 este egală cu valoarea funcției în acest punct, adică . Această proprietate nu este valabilă pentru funcția prezentată în fig. nr. 4.

Proprietățile care sunt satisfăcute pentru funcția prezentată în fig. Nr. 3 și face posibilă definirea unei funcții continue într-un punct x 0 .

Definiție: Se spune că funcția este continuă într-un punct x 0, dacă .

cometariu: Dacă funcția este continuă într-un punct x 0, apoi punct x 0 se numește punct de continuitate al unei funcții dacă funcția nu este continuă în punctul respectiv x 0, apoi punct x 0 se numește punctul de întrerupere a funcției.

Definiție: O funcție se numește continuă pe un interval dacă este continuă în fiecare punct din acel interval.

5. Argument increment, function increment

Fie dată funcția ,.

x 0 - valoarea inițială a argumentului, ;

X- valoarea finală a argumentului, ;

f (x 0) - valoarea inițială a funcției;

f(x 0 + D x) - valoarea finală a funcției.

Definiție: Diferența dintre valorile de sfârșit și de început ale argumentului se numește increment al argumentului. D x \u003d x - x 0

Definiție: Diferența dintre valorile finale și inițiale ale funcției se numește increment al funcției. D y \u003d f (x 0 + D x) - f (x 0)

cometariu:

Incrementarea geometrică a argumentului D x– este diferența dintre abscisele punctelor graficului funcției corespunzătoare valorilor finale și inițiale ale argumentului.
Funcția de incrementare geometrică D y– este diferența dintre ordonatele punctelor graficului funcției corespunzătoare valorilor finale și inițiale ale argumentului.
Creșterea argumentului și a funcției pot fi pozitive sau negative.

6. Conceptul de derivată a unei funcții. sens fizic funcţie derivată

Luați în considerare problema ratei de modificare a funcției , unde X Și la poate fi orice mărime fizică.

x 0 - valoarea inițială a argumentului; f (x 0) - valoarea inițială a funcției;

x 0 +D x - valoarea finală a argumentului; f(x 0 + D x) - valoarea finală a funcției;

D y \u003d f (x 0 + D x) - f (x 0) - creșterea funcției;

– rata medie de modificare a unei funcții într-un interval D x .

– viteza instantanee de modificare a unei funcții, rata de modificare a unei funcții într-un punct x 0.

Definiție: Derivată a unei funcții într-un punct x 0 se numește limita raportului de creștere D funcţionează la un punct x 0 a incrementa D x argument când incrementul argumentului tinde spre zero.

Ieșire: Derivată a unei funcții într-un punct x 0 este rata de schimbare a funcției în punct x 0.

Teorema: Derivată a unei funcții constante y = cîn orice moment este egal cu zero.

Teorema: Derivată a unei funcții y = xîn orice moment egal cu unu .

cometariu: Găsirea derivatei unei funcții date se numește diferențiere.

7. Reguli de diferențiere a sumei, produsului, coeficientului de funcții

Luați în considerare funcția , constând din alte două funcții și , având derivate pe segment:

3) .

Teorema #1: Derivata sumei (diferența) a două funcții este egală cu suma (diferența) derivatelor acestor funcții.

Exemplu: Calculați derivata unei funcții

Teorema #2: Derivata produsului a doua functii este determinata de formula:

Consecinţă: Factorul constant poate fi scos din semnul derivatei: .

Dovada: .

Exemplu

Exerciții:

2) ;

Derivata functiei putere la se calculeaza prin formula:

cometariu: Formula este valabilă pentru o funcție de putere cu orice exponent. ,

Exemplu: Calculați derivatele funcțiilor:

Ieșire: .

Exerciții: Calculați derivatele funcțiilor:

; 2) ; 3) ;

4) ; 5) ;

6) ; 7) .

Teorema #3: Derivata coeficientului a doua functii este determinata de formula:

Consecințe: ;

Exemplu: Calculați derivatele funcțiilor:

2) . .

3) . .

Exerciții: Calculați derivatele funcțiilor:

1. ; 2. ; 3. ;

4. ; 5. ; 6.

;

; 8. ; 9.

8. Conceptul de funcție complexă

Regula de diferențiere a funcției complexe

Lăsați funcția să fie definită pe set și funcția pe set și pentru valoarea corespunzătoare. Apoi este definită o funcție pe set, care este numită functie complexa din X (funcție din funcție).

O variabilă se numește argument intermediar al unei funcții complexe.

Exemplu:

Exerciții:

De la ce functii elementare Aceste funcții complexe constau în:

1) ; 2) ;

; 4) .

Compuneți funcții complexe din aceste funcții elementare:

1) , ; 2) , ;

3) , . 4) , , .

Ieșire: Derivata unei functii complexe este egala cu produsul derivatelor functiilor elementare care o alcatuiesc .

Exemplu: Calculați derivatele funcțiilor:

- putere, liniară; , .

- putere, pătratică; , .

Exerciții: Calculați derivatele funcțiilor:

1. ; 2.

;

3. ; 4. ;

; 6. .

9. Derivată a funcţiilor exponenţiale, logaritmice

Exemplu: Calculați derivatele funcțiilor:

1. . .

2. . .

3. . .

Exemplu: Calculați derivatele funcțiilor:

1. . .

2. . .

Exerciții: Calculați derivata unei funcții:

1. ; 2. ; 3. ;

4. ; 5. ; 6. ;

7. ; 8. .

10. Derivate ale funcţiilor trigonometrice

Derivate ale funcţiilor trigonometrice inverse

Exemplu: Calculați derivatele funcțiilor:

1. . .

2. . .

O sarcină

. .

O sarcină: Calculați derivata funcției .

Exercitiul: Calculați derivata funcției .

Derivate ale funcţiilor trigonometrice inverse

;

Exerciții: Calculați derivatele funcțiilor:

1. 2.

3. 4.

5. 6. 7. 8. 9.

10.

11. 12. 13.

11. sens geometric funcţie derivată

Să luăm în considerare o funcție.

Luați un punct fix pe graficul funcției și un punct arbitrar . Să desenăm o secanta . Dacă punctul M trece la infinit la un punct M 0 conform graficului funcției , apoi secantei M 0 M va ocupa pozitii diferite si daca punctul coincide M cu un punct M 0 secanta va lua poziția limită M 0 T , apoi linia dreaptă M 0 T va fi tangentă la graficul funcției din punct M 0 .

Definiție: Tangenta la graficul functiei la punct M 0 numită limită M 0 T secantă în timp ce se străduiește pentru un punct M conform programului la obiect M 0 .

b- unghiul de înclinare al secantei M 0 M

A- unghiul de înclinare al tangentei M 0 T pe direcția pozitivă a axei x.

Panta secantei M 0 M .

Pantă tangentă M 0 T .

Luați în considerare un triunghi dreptunghic M 0 MA (). Tangenta unghiului acut triunghi dreptunghic egal cu raportul dintre piciorul opus și cel adiacent:

i.e . Si asta inseamnă .

Definiți derivata funcției într-un punct x 0 : .

, , Prin urmare, .

Ieșire: Sensul geometric al derivatei funcției este că derivata funcției la este egală cu panta tangentei trasate la graficul funcției în punctul cu abscisa.

Exemplu:

1. Aflați panta tangentei trasate la graficul funcției în puncte .

; ; ; ; ; .

Răspuns: ; ; .

2. Aflați unghiul de înclinare al tangentei trasate la graficul funcției în punctul cu abscisa.

; ; ; ; . paralel cu o linie dreaptă;

Hai să instalăm conditie necesara existența unui extremum.

teorema lui Fermat: Dacă punctul interior x 0 fara scop functie continua este un punct extremum și în acest punct există o derivată, atunci este egală cu zero.

cometariu: Totuși, egalitatea la zero a derivatei funcției în punctul x 0 încă nu dă dreptul de a pretinde că x 0 – punctul extremum al funcției.

Când obținem prima formulă a tabelului, vom porni de la definiția derivatei unei funcții într-un punct. Să luăm unde X- orice număr real, adică X– orice număr din zona de definire a funcției . Să scriem limita raportului dintre incrementul funcției și incrementul argumentului la:

De remarcat că sub semnul limitei se obține o expresie, care nu este incertitudinea zero împărțită la zero, întrucât numărătorul nu conține o valoare infinitezimală, ci exact zero. Cu alte cuvinte, incrementul unei funcții constante este întotdeauna zero.

În acest fel, derivata unei functii constanteeste egal cu zero pe întregul domeniu de definiție.

Derivată a unei funcții de putere.

Formula pentru derivata unei funcții putere are forma , unde exponentul p este orice număr real.

Să demonstrăm mai întâi formula exponentului natural, adică pentru p = 1, 2, 3, ...

Vom folosi definiția unei derivate. Să scriem limita raportului dintre incrementul funcției de putere și incrementul argumentului:

Pentru a simplifica expresia în numărător, ne întoarcem la formula binomială a lui Newton:

Prin urmare,

Aceasta dovedește formula pentru derivata unei funcții de putere pentru un exponent natural.

Derivată a funcției exponențiale.

Deducem formula derivată pe baza definiției:

A ajuns la incertitudine. Pentru a o extinde, introducem o nouă variabilă și pentru . Apoi . În ultima tranziție, am folosit formula pentru trecerea la o nouă bază a logaritmului.

Să efectuăm o înlocuire în limita inițială:

Dacă ne amintim a doua limită remarcabilă, atunci ajungem la formula pentru derivata funcției exponențiale:

Derivată a unei funcții logaritmice.

Să demonstrăm formula pentru derivata funcției logaritmice pentru toate X din domeniul de aplicare și toate valorile de bază valide A logaritm. Prin definiția derivatei, avem:

După cum ați observat, în demonstrație, transformările au fost efectuate folosind proprietățile logaritmului. Egalitate este valabilă datorită celei de-a doua limite remarcabile.

Derivate ale funcţiilor trigonometrice.

Pentru a deriva formule pentru derivate ale funcțiilor trigonometrice, va trebui să reamintim câteva formule de trigonometrie, precum și prima limită remarcabilă.

Prin definiția derivatei pentru funcția sinus, avem .

Folosim formula pentru diferența de sinusuri:

Rămâne să ne întoarcem la prima limită remarcabilă:

Deci derivata funcției sin x mânca cos x.

Formula pentru derivata cosinus este dovedită exact în același mod.

Prin urmare, derivata funcției cos x mânca –sin x.

Derivarea formulelor pentru tabelul de derivate pentru tangentă și cotangentă se va efectua folosind regulile dovedite de diferențiere (derivată a fracției).

Derivate ale funcțiilor hiperbolice.

Regulile de diferențiere și formula pentru derivata funcției exponențiale din tabelul derivatelor ne permit să derivăm formule pentru derivatele sinusului hiperbolic, cosinusului, tangentei și cotangentei.

Derivată a funcției inverse.

Pentru ca în prezentare să nu existe confuzie, să notăm în indexul inferior argumentul funcției prin care se realizează diferențierea, adică este derivata funcției f(x) pe X.

Acum formulăm regula pentru aflarea derivatei functiei inverse.

Lasă funcțiile y = f(x)Și x = g(y) reciproc invers, definite pe intervale și respectiv. Dacă într-un punct există o derivată finită nenulă a funcției f(x), atunci în punctul există o derivată finită a funcției inverse g(y), și . Într-o altă intrare .

Această regulă poate fi reformulată pentru orice X din intervalul , atunci obținem .

Să verificăm validitatea acestor formule.

Să găsim funcția inversă pentru logaritmul natural (Aici y este o funcție și X- argument). Rezolvarea acestei ecuații pentru X, primim (aici X este o funcție și y argumentul ei). adica și funcții reciproc inverse.

Din tabelul derivatelor, vedem că Și .

Să ne asigurăm că formulele pentru găsirea derivatelor funcției inverse ne conduc la aceleași rezultate:

După cum puteți vedea, am obținut aceleași rezultate ca și în tabelul de derivate.

Acum avem cunoștințele pentru a demonstra formule pentru derivatele funcțiilor trigonometrice inverse.

Să începem cu derivata arcsinusului.

. Apoi, prin formula pentru derivata funcției inverse, obținem

Rămâne de realizat transformarea.

Deoarece intervalul arcsinusului este intervalul , apoi (vezi secțiunea privind funcțiile elementare de bază, proprietățile și graficele acestora). Prin urmare, nu luăm în considerare.