Equazioni canoniche della retta

Formulazione del problema. Trova le equazioni canoniche di una retta definita come una linea di intersezione di due piani (equazioni generali)

Piano di soluzione. Equazioni canoniche di una retta con un vettore di direzione Passare attraverso dato punto , avere il modulo

. (1)

Pertanto, per scrivere le equazioni canoniche di una retta, è necessario trovare il suo vettore direttivo e un punto della retta.

1. Poiché la linea appartiene a entrambi i piani contemporaneamente, il suo vettore di direzione è ortogonale ai vettori normali di entrambi i piani, cioè secondo la definizione di prodotto vettoriale, abbiamo

. (2)

2. Scegli un punto sulla linea. Poiché il vettore di direzione della linea non è parallelo ad almeno uno dei piani delle coordinate, la linea interseca questo piano delle coordinate. Pertanto, come punto su una retta, può essere preso il punto della sua intersezione con questo piano di coordinate.

3. Sostituiamo le coordinate trovate del vettore direttivo e puntiamo nelle equazioni canoniche della retta (1).

Commento. Se il prodotto vettoriale (2) è uguale a zero, i piani non si intersecano (in parallelo) e non è possibile scrivere le equazioni canoniche della retta.

Compito 12. Scrivi le equazioni canoniche della retta.

Equazioni canoniche di una retta:

,

dove sono le coordinate di qualsiasi punto della retta, è il suo vettore di direzione.

Trova un punto qualsiasi della linea . Lascia allora

Di conseguenza, sono le coordinate di un punto appartenente alla retta.

Per ogni retta nello spazio passa un numero infinito di piani. Due di loro, intersecantisi, lo definiscono nello spazio. Pertanto, le equazioni di due piani qualsiasi, considerati insieme, sono le equazioni di questa retta.

In generale, due qualsiasi piani paralleli data dalle equazioni generali

determinare la loro linea di intersezione. Queste equazioni sono chiamate equazioni generali dritto

Biglietto 6 Scrivi un'espressione per l'angolo tra una retta e un piano, la condizione di parallelismo e perpendicolarità di una retta e un piano.

angolo tra una retta ed un piano chiameremo l'angolo formato dalla retta e la sua proiezione sul piano. Sia il piano dato dalle equazioni

Considera vettori e . Se l'angolo tra loro è acuto, allora sarà , dove φ è l'angolo tra la linea e il piano. Quindi .

Se l'angolo tra i vettori e è ottuso, allora è uguale a . Di conseguenza . Pertanto, in ogni caso. Ricordando la formula per calcolare il coseno dell'angolo tra i vettori, otteniamo .

La condizione di perpendicolarità di una retta e di un piano. Una retta e un piano sono perpendicolari se e solo se il vettore di direzione della retta e il vettore normale del piano sono collineari, cioè .

Condizione di parallelismo di una retta e di un piano. Una retta e un piano sono paralleli se e solo se i vettori e sono perpendicolari.

Biglietto 7. Definisci un'ellisse. Scrivi l'equazione dell'ellisse in forma canonica. Vertici, fuochi, assi ed eccentricità dell'ellisse.

Definizione: Un'ellisse è il luogo dei punti di un piano, per ciascuno dei quali la somma delle distanze di due punti dati dello stesso piano, detti fuochi dell'ellisse, è un valore costante.

Lascia stare F 1 e F 2 - fuochi dell'ellisse. Cominciare o i sistemi di coordinate si trovano al centro del segmento F 1 F 2. Asse Bue diretto lungo questo segmento, l'asse Ehi- perpendicolare a questo segmento (Fig.).

Definizione: Si chiamano i punti di intersezione di un'ellisse con i suoi assi di simmetria ellisse di vertice a, il centro di simmetria è il centro dell'ellisse, viene chiamato il segmento tra due vertici contenenti fuochi asse maggiore dell'ellisse, metà della sua lunghezza semiasse maggiore di un'ellisse. Viene chiamato il segmento tra i vertici sull'asse di simmetria che non contiene fuochi asse minore dell'ellisse, metà della sua lunghezza è il semiasse minore. Il valore viene chiamato eccentricità dell'ellisse.

Se l'ellisse è data da equazioni canoniche, i suoi vertici hanno coordinate (– un;0), (un;0),(0; –B), (0;B), il semiasse maggiore è un, il semiasse minore è uguale a B. Valore C, che è la metà della distanza tra i fuochi, è determinata dalla formula C 2 = un 2 – B 2 .

L'eccentricità dell'ellisse caratterizza il grado di allungamento dell'ellisse. Più l'eccentricità è vicina a zero, più l'ellisse appare come un cerchio. Più l'eccentricità è vicina a 1, più l'ellisse è allungata. Si noti che, per definizione, per un'ellisse 0< <1.

L'equazione è chiamata l'equazione canonica dell'ellisse.

Biglietto 8 Definisci l'iperbole. Scrivi l'equazione dell'iperbole in forma canonica. Vertici, fuochi, assi, asintoti ed eccentricità dell'iperbole,

Definizione: Un'iperbole è un luogo di punti in un piano, per ciascuno dei quali il valore assoluto della differenza di distanze da due punti fissi dello stesso piano, detti fuochi dell'iperbole, è un valore costante.

Proprio come nel caso di un'ellisse, per ottenere l'equazione di un'iperbole, scegliamo un sistema di coordinate appropriato. L'origine delle coordinate si trova nel mezzo del segmento tra i fuochi, l'asse Bue diretto lungo questo segmento e l'asse y è perpendicolare ad esso.

L'equazione è chiamata equazione canonica iperbole.

Un'iperbole ha due assi di simmetria reciprocamente perpendicolari, uno dei quali contiene i fuochi dell'iperbole e un centro di simmetria. Se un'iperbole è data da un'equazione canonica, i suoi assi di simmetria sono gli assi delle coordinate Bue e Ehi, e l'origine è il centro di simmetria dell'iperbole.

Definizione: Punti di intersezione dell'iperbole dati dall'equazione canonica con l'asse Bue chiamata vertici dell'iperbole, viene chiamato il segmento tra di loro l'asse reale dell'iperbole. Il segmento dell'asse y tra i punti (0;– B) e (0; B) è chiamato asse immaginario. Numeri un e B sono chiamati rispettivamente semiassi reale e immaginario dell'iperbole. L'origine delle coordinate è chiamata centro. Il valore viene chiamato eccentricità iperbole.

Commento: Dall'uguaglianza B 2 = C 2 – un 2 ne consegue che C>un, cioè l'iperbole >1. L'eccentricità caratterizza l'angolo tra gli asintoti, più vicino a 1, più piccolo è questo angolo.

Biglietto 9. Definisci una parabola. Scrivi l'equazione della parabola in forma canonica. Direttrice, fuoco di una parabola

Una parabola è il luogo dei punti di un piano equidistanti da un dato punto F e da una data retta d che non passa per un dato punto. Questa definizione geometrica esprime proprietà directory parabola.

La proprietà direzionale di una parabola Il punto F si chiama fuoco della parabola, la retta d si chiama direttrice della parabola, il punto medio O della perpendicolare caduta dal fuoco alla direttrice è il vertice della parabola, la distanza p dal fuoco alla direttrice è il parametro della parabola e la distanza p2 dal vertice della parabola al suo fuoco è la distanza del fuoco (Fig. a). La retta perpendicolare alla direttrice e passante per il fuoco è chiamata asse della parabola (l'asse focale della parabola). Il segmento FM che collega un punto arbitrario M della parabola con il suo fuoco è chiamato raggio focale del punto M. Il segmento che collega due punti della parabola è chiamato corda della parabola.

Per un punto arbitrario della parabola, il rapporto tra la distanza dal fuoco e la distanza dalla direttrice è uguale a uno. Confrontando le proprietà della directory dell'ellisse, dell'iperbole e della parabola, ne concludiamo eccentricità della parabolaè per definizione uguale a uno

.Definizione geometrica parabole , esprimendo la sua proprietà directory, equivale alla sua definizione analitica - la retta data dall'equazione canonica della parabola:

Biglietto 10. Che cos'è una matrice quadrata, identitaria, simmetrica, ortogonale. Definisci trasposto e matrici inverse S.

Definizione 1.Matriceè chiamata tabella rettangolare di numeri contenente - righe e - colonne. .

Definizione 2. Numeri e sono chiamati Ordini a matrice(o dire che la matrice ha dimensioni)

Definizione 3. I numeri che compongono questa matrice sono detti suoi elementi.

1. Definizione 4. Viene chiamata la matrice Quadrato se il numero di righe è uguale al numero di colonne. quando matrice quadrata vengono introdotti i concetti diagonale principale(questi sono numeri - ) e Diagonale laterale(questi sono numeri - ).

2. Simmetrico Una matrice (simmetrica) è una matrice quadrata i cui elementi sono simmetrici rispetto alla diagonale principale. Più formalmente, una matrice si dice simmetrica se .

Ciò significa che è uguale alla sua matrice trasposta:

3. Matrice di identità è chiamata matrice diagonale in cui tutti gli elementi diagonali sono uguali a uno. Ad esempio, la matrice identità del terzo ordine è la matrice

matrice ortogonale

matrice quadrata UN, per cui LA -1 = LA T chiamata matrice ortogonale. Proprietà di base di una matrice ortogonale: Il modulo del determinante di una matrice ortogonale è uguale a uno. Questa proprietà deriva dalle proprietà dei determinanti:

La somma dei quadrati degli elementi di qualsiasi colonna di una matrice ortogonale è uguale a uno.

Prodotto scalare la riga su se stessa è 1 e su qualsiasi altra riga è 0. Lo stesso per le colonne.

La somma dei prodotti degli elementi di qualsiasi riga di una matrice ortogonale per gli elementi corrispondenti di un'altra riga è uguale a zero.

matrice inversa è una matrice che, moltiplicata sia a destra che a sinistra per una data matrice, dà la matrice identità.Denota l'inversa della matrice MA attraverso , quindi secondo la definizione otteniamo: dove eè la matrice dell'identità.

La matrice inversa non esiste per tutte le matrici. Necessario e condizione sufficiente la non degenerazione è

det( UN) ≠ 0 o rango( UN) = n.

Proprietà delle matrici inverse

· , dove denota il determinante.

per due qualsiasi matrici invertibili E .

· , dove denota la matrice trasposta.

· per qualsiasi coefficiente.

Se hai bisogno di risolvere il sistema equazioni lineari, (b è un vettore diverso da zero) dove è il vettore desiderato e, se esiste, allora . Altrimenti, la dimensione dello spazio della soluzione è maggiore di zero o non ce ne sono affatto.

Matrice trasposta- matrice ottenuta dalla matrice originale sostituendo le righe con le colonne.

Formalmente, la matrice di trasposizione per la matrice delle dimensioni è la matrice delle dimensioni, definita come .

Biglietto 11. Cosa sono le matrici equivalenti. Elenca le trasformazioni elementari delle matrici. Cosa si può dire dei ranghi di matrici equivalenti.

Definizione. Si chiamano le matrici ottenute come risultato di una trasformazione elementare equivalente.

Trasformazioni elementari su righe di matrici si chiamano le seguenti trasformazioni di stringhe:

1. moltiplicare una stringa per un numero diverso da zero;

2. permutazione di due linee;

3. somma ad una riga della matrice dell'altra riga, moltiplicata per un numero diverso da zero.

4. Se una matrice viene passata da una matrice all'altra con l'aiuto di trasformazioni equivalenti su righe, tali matrici vengono chiamate equivalente e denota.

5. Metodo delle trasformazioni elementari

6. Classificazione della matrice è uguale al numero righe diverse da zero nella matrice dopo averlo portato a una forma a gradini utilizzando trasformazioni elementari sulle righe della matrice.

Biglietto 12 Cos'è una base minore. Enuncia il teorema minore di base.

Definizione. Il rango della matrice A è l'ordine massimo del minore diverso da zero (il minore è il determinante di una matrice quadrata). Designato.

Definizione. Il minore che determina il rango della matrice è detto Basis Minor. Le righe e le colonne che formano il BM sono chiamate righe e colonne di base.

Definizione. Sistema a colonne è detto numeri linearmente dipendenti, non tutti uguali a zero e tali che:

Teorema di base minore

Le colonne della matrice incluse nella base minore formano un sistema linearmente indipendente. Qualsiasi colonna della matrice è espressa linearmente in termini di colonne rimanenti dalla minore di base.

Nella matrice delle dimensioni, un minore dell'ordine -esimo si dice elementare se è diverso da zero e tutti i minori dell'ordine -ro sono uguali a zero o non esistono affatto.

Conseguenza. Se tutte le colonne di una matrice sono espresse linearmente in termini di colonne che formano un sistema linearmente indipendente, allora il rango della matrice è.

Biglietto 13 Che cos'è un sistema di equazioni omogeneo e non omogeneo. Quella che viene chiamata la soluzione di un sistema di equazioni. Spiega i termini: sistema di equazioni compatibile, sistema di equazioni incompatibile. Quali sistemi di equazioni sono detti equivalenti?

Definizione 1. Se tutti i termini liberi sono uguali a zero, il sistema è chiamato omogeneo ed eterogeneo, altrimenti.

Definizione 2. La soluzione del sistema è l'insieme di n numeri da 1 , da 2 , …, da n , quando si sostituisce nel sistema, invece di incognite, m identità numeriche.

Definizione 3. Un sistema si dice compatibile (incompatibile) se ha almeno una soluzione (non ha soluzioni).

Definizione 4. Sistema lineare unito equazioni algebriche si dice definito (indefinito) se ha una soluzione unica (un insieme di soluzioni).

Definizione.

Si chiamano due sistemi di equazioni lineari equivalente (equivalente), se hanno le stesse soluzioni.

Sistemi equivalenti si ottengono, in particolare, quando trasformazioni elementari system, a condizione che le trasformazioni vengano eseguite solo sulle stringhe di sistema.

Biglietto 14 Che cos'è un sistema decisionale fondamentale sistema omogeneo equazioni. Quella che viene chiamata la soluzione generale di un sistema omogeneo di equazioni.

Definizione. La base dello spazio delle soluzioni di un sistema di equazioni lineari omogenee è chiamata sua sistema decisionale fondamentale.

Teorema sulla struttura della soluzione generale di un sistema omogeneo di equazioni:

Qualsiasi soluzione di un sistema omogeneo di equazioni lineari è definita dalla formula

dove X 1 , X 2 , … , X n − R- sistema fondamentale di soluzioni di un sistema omogeneo di equazioni lineari e C 1 , C 2 , … , C n − R sono costanti arbitrarie.

Proprietà della soluzione generale di un sistema omogeneo di equazioni:

1. Per qualsiasi valore C 1 , C 2 , … , C n − R X, definito dalla formula (3), è una soluzione del sistema (1).

2. Qualunque sia la decisione X 0 , ci sono numeri C 1 0 , … , C n − R 0 tale che

Produzione: Trovare sistema fondamentale e la soluzione generale del sistema omogeneo, è necessario trovare la base del kernel del corrispondente operatore lineare.

Biglietto 16. Dare una definizione di spazio lineare e formularne le proprietà.

Molti l chiamata lineare o spazio vettoriale , se per tutti gli elementi (vettori) di questo insieme sono definite le operazioni di addizione e moltiplicazione per un numero ed è vero:

1. Ogni coppia di elementi X e y da l incontra l'elemento X + y da l , chiamata sommaX e y, e:

X + y = y+x− l'addizione è commutativa;

X + (s + z) = (x + y) + z− l'addizione è associativa;

X +0 = X− ce n'è solo uno nullo elemento 0 (X +0 = X per chiunque X da l );

X + (− X)= 0 − per ogni elemento X da l ce n'è solo uno opposto elemento −x (x + (−x) = 0 per chiunque X da l) .

2. Ogni coppia X e α, dove α − numero, e X elemento da l , corrisponde all'elemento α X, chiamata lavoroα eX, e:

α·(β · X) = (α·β) · X− la moltiplicazione per un numero è associativa: ;

1· X = X− per qualsiasi elemento X da l .

3. Le operazioni di addizione e moltiplicazione per un numero sono legate dalle relazioni:

α·( X + y) = α· X + α· y− la moltiplicazione per un numero è distributiva rispetto all'addizione di elementi;

(α + β )· X = α· X + β · X− la moltiplicazione per un vettore è distributiva rispetto all'addizione di numeri.

Biglietto 17. Un sottospazio di uno spazio lineare. Le sue proprietà. Conchiglia lineare.

Definizione di sottospazio lineare

Viene chiamato un sottoinsieme L non vuoto di uno spazio lineare V sottospazio lineare spazio V se

1) u+v∈L ∀u,v∈L (il sottospazio è chiuso rispetto all'operazione di addizione);

2) λv∈L ∀v∈L e qualsiasi numero λ (il sottospazio è chiuso rispetto all'operazione di moltiplicazione di un vettore per un numero).

Proprietà 1 Qualsiasi sottospazio di uno spazio lineare R è uno spazio lineare.

Proprietà 2 dim M ≤ dim Rn.

Proprietà 3 (a completamento della base). Se (ep)k è una base in un sottospazio M di uno spazio lineare Rn, e k< n, то можно так выбрать элементы в Rn ek+1, ek+2, . . . , en, что (ep)n будет базисом в Rn.

Definizione. Guscio lineareè un insieme di vettori che definiscono un sottospazio lineare. In senso stretto, guscio lineareè l'insieme di tutti combinazioni lineari vettori di dati. Evidenziamo anche le caratteristiche:

Biglietto 18. Definisci lo spazio euclideo. Spiegare l'operazione di normalizzazione del vettore.

Definizione Sia V uno spazio vettoriale. Diciamo che a V è dato un prodotto interno se sono assegnati due vettori x, y ∈ V qualsiasi numero reale, chiamato prodotto interno di questi vettori e indicato con xy o (x, y), in modo che siano soddisfatte le seguenti condizioni (qui x, y, z sono vettori arbitrari da V e

t è un numero reale arbitrario):

1) xy = yx (il prodotto scalare è commutativo);

2) (tx)y = t(xy);

3) (x + y)z = xz + yz (il prodotto scalare è distributivo rispetto all'addizione);

4) xx >=0 e xx = 0 se e solo se x = 0.

spazio vettoriale, in cui è dato il prodotto scalare, è detto euclideo. Le proprietà 1)–4) sono dette assiomi dello spazio euclideo.

Chiamata vettoriale normalizzato o singolare se la sua lunghezza è uguale a uno. Normalizzare un vettore arbitrario diverso da zero significa dividerlo per la sua lunghezza. Si scopre vettore unitario, co-diretto all'originale.
Il prodotto scalare di un vettore arbitrario per un'unità darà la lunghezza esatta della proiezione di questo vettore sulla direzione dell'unità. Per ottenere non solo la lunghezza, ma il vettore di proiezione stesso, dobbiamo moltiplicare questa lunghezza per il nostro vettore unitario:

Biglietto 19 Che cos'è una base ortonormale. Spiegare il processo di ortogonalizzazione di Gram-Schmidt utilizzando una base bidimensionale come esempio.

Sistema ortonormale composto da n vettori n-spazio euclideo dimensionale, costituisce la base di questo spazio. Tale base è chiamata Ortonormale base.

Se e 1 , e 2 , ..., esn -Ortonormale base n-spazio euclideo dimensionale e

X = X 1 e 1 + X 2 e 2 + ... + X n e n - decomposizione vettoriale X su questa base, quindi le coordinate Xio vettore X in base ortonormale sono calcolati dalle formule Xio =(x, eio ), io= 1, 2, ..., n.

GRAMA-SCHMIDT, Dato un sistema di vettori linearmente indipendente b 1 , b 2 , …, b l , a l+1 , …, a n l ≥ 1(1) indichiamo la parte a cui è ortogonale bl+1 componente ortogonale del vettore e l+1 rispetto al sistema ortogonale b 1 , b 2 , …, b l Allora 1. Sistema vettoriale b 1 , b 2 , …, b l , b l+1 , a l+2 , …, a n(2) è equivalente a (1).

2. Il sistema dei vettori (2) è linearmente indipendente, e la sua parte b 1 , b 2 , …, b l , b l+1– ortogonale Usando il concetto di componente ortogonale, descriviamo il processo di trasformazione di un sistema linearmente indipendente a 1 , a 2 , …, a n in sistema ortogonaleb 1 , b 2 , …, b n vettori diversi da zero, che viene chiamato ortogonalizzazione del sistema a 1 , a 2 , …, a n.Questo processo consiste di n passaggi, n è il numero di vettori nel sistema originale a 1 , a 2 , …, a n.

1 passo. Noi crediamo b 1 \u003d a 1 e prendi il sistema b 1 , a 2 , …, a n

2 gradini. Sostituiamo il vettore nel sistema (3) un 2 componente ortogonale rispetto a b 1, e otteniamo il sistema: b 1 ,b 2 , a 3 ,…, a n (4)

Secondo le fasi di ortogonalizzazione, il sistema (4) è linearmente indipendente, e la sua parte b 1, b 2-ortogonale.

Supponiamo di aver già costruito un sistema linearmente indipendente b 1 , b 2 , …, b k-1 , a k ,…, a n, (5)

in quale b 1 , b 2 , …, b k-1 sono ortogonali.

Al k-esimo passo k = 3, n, sostituiamo il vettore nel sistema (5) un k la sua componente ortogonale rispetto al sistema b 1 , b 2 , …, b k-1 e prendi il sistema b 1 , …,b k , a k+1 , …, a n.

Dopo aver eseguito l'ennesimo passaggio, otteniamo un sistema di vettori linearmente indipendente e ortogonale b 1 , b 2 , …, b n.

Biglietto 20.Definire un operatore in uno spazio lineare. Quale operatore si chiama lineare.

Operatore detta regola secondo cui ogni elemento X X un singolo elemento è abbinato y qualche set non vuoto Y . Si dice che l'operatore agisca da X in Y .

L'azione dell'operatore è indicata y = UN (X), y- Immagine X, X- prototipo y.

Se ogni elemento y da Y ha un'unica preimmagine X da X , y= UN (X), viene chiamato l'operatore mappatura uno a uno X in Y o trasformazione X , X - ambito di definizione dell'operatore.

Lascia stare X e Y due spazi lineari. Operatore UN agendo da X in Y , è chiamato operatore di linea, se per due elementi qualsiasi tu e v da X e qualsiasi numero α è valido:

UN(tu+ v) = UN (tu) + UN (v) , UN (α· tu) = α· UN (tu).

Biglietto 21. Fai un esempio di operatore lineare. Quali operazioni sugli operatori lineari conosci?

IN questa sezione Continuiamo lo studio del tema dell'equazione di una retta nello spazio dal punto di vista della stereometria. Ciò significa che considereremo una retta nello spazio tridimensionale come una linea di intersezione di due piani.

Secondo gli assiomi della stereometria, se due piani non coincidono e hanno un punto in comune, allora hanno anche una retta comune, su cui giacciono tutti i punti comuni ai due piani. Usando le equazioni di due piani intersecanti, possiamo definire una retta in un sistema di coordinate rettangolare.

Nel corso della trattazione dell'argomento verranno forniti numerosi esempi, alcune illustrazioni grafiche e soluzioni dettagliate necessarie per una migliore assimilazione del materiale.

Siano dati due piani che non coincidono tra loro e si intersecano. Indichiamoli come il piano α e il piano β . Mettiamoli in un sistema di coordinate rettangolare O x y z spazio tridimensionale.

Come ricordiamo, qualsiasi piano in un sistema di coordinate rettangolare definisce l'equazione generale del piano della forma A x + B y + C z + D = 0 . Assumiamo che il piano α corrisponda all'equazione A 1 x + B 1 y + C 1 z + D 1 = 0 e il piano β corrisponda all'equazione A 2 x + B 2 y + C 2 z + D 2 = 0. In questo caso, i vettori normali dei piani α e β n 1 → \u003d (A 1, B 1, C 1) e n 2 → \u003d (A 2, B 2, C 2) non sono collineari, poiché il i piani non coincidono tra loro e sono posti paralleli tra loro. Scriviamo questa condizione come segue:

n 1 → ≠ λ n 2 → ⇔ UN 1 , B 1 , C 1 ≠ λ UN 2 , λ B 2 , λ C 2 , λ ∈ R

Per aggiornare il materiale sull'argomento "Parallelismo degli aerei", vedere la sezione corrispondente del nostro sito Web.

La linea di intersezione dei piani sarà indicata dalla lettera un . Quelli. a = α ∩ β . Questa linea è un insieme di punti comuni a entrambi i piani α e β. Ciò significa che tutti i punti della retta a soddisfano entrambe le equazioni del piano A 1 x + B 1 y + C 1 z + D 1 = 0 e A 2 x + B 2 y + C 2 z + D 2 = 0 . In effetti, sono una soluzione particolare del sistema di equazioni A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 .

La soluzione generale del sistema di equazioni lineari A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 determina le coordinate di tutti i punti della retta lungo il quale l'intersezione di due piani α e .beta. Ciò significa che con il suo aiuto possiamo determinare la posizione di una retta in un sistema di coordinate rettangolare O x y z .

Consideriamo ancora una volta la teoria descritta, ora con un esempio specifico.

Esempio 1

La linea O x è la linea lungo la quale si intersecano i piani delle coordinate O x y e O x z. Definiamo il piano O x y con l'equazione z = 0, e il piano O x z con l'equazione y = 0. Abbiamo discusso questo approccio in dettaglio nella sezione "Equazione generale incompleta di un piano", quindi, in caso di difficoltà, possiamo fare nuovamente riferimento a questo materiale. In questo caso, la linea di coordinate O x è determinata in un sistema di coordinate tridimensionale da un sistema di due equazioni della forma y = 0 z = 0 .

Trovare le coordinate di un punto che giace su una retta lungo la quale i piani si intersecano

Consideriamo il compito. Sia dato un sistema di coordinate rettangolare O x y z nello spazio tridimensionale. La retta lungo la quale due piani si intersecano a è data dal sistema di equazioni A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 . Dato un punto nello spazio tridimensionale M 0 x 0 , y 0 , z 0 .

Determiniamo se il punto M 0 x 0 , y 0 , z 0 appartiene ad una retta data un .

Per ottenere una risposta alla domanda del problema, sostituiamo le coordinate del punto M 0 in ciascuna delle due equazioni del piano. Se, per sostituzione, entrambe le equazioni diventano vere uguaglianze A 1 x 0 + B 1 y 0 + C 1 z 0 + D 1 = 0 e A 2 x 0 + B 2 y 0 + C 2 z 0 + D 2 = 0, allora il punto M 0 appartiene a ciascuno dei piani e appartiene alla retta data. Se almeno una delle uguaglianze A 1 x 0 + B 1 y 0 + C 1 z 0 + D 1 = 0 e A 2 x 0 + B 2 y 0 + C 2 z 0 + D 2 = 0 è falsa, allora il punto M 0 non appartiene ad una retta.

Considera una soluzione di esempio

Esempio 2

Una retta è data nello spazio dalle equazioni di due piani intersecanti della forma 2 x + 3 y + 1 = 0 x - 2 y + z - 3 = 0 . Determinare se i punti M 0 (1, - 1, 0) e N 0 (0, - 1 3 , 1) appartengono a una retta di intersezione dei piani.

Soluzione

Partiamo dal punto M 0 . Sostituisci le sue coordinate in entrambe le equazioni del sistema 2 1 + 3 (- 1) + 1 = 0 1 - 2 (- 1) + 0 - 3 = 0 ⇔ 0 = 0 0 = 0 .

Come risultato della sostituzione, abbiamo ottenuto le uguaglianze corrette. Ciò significa che il punto M 0 appartiene a entrambi i piani e si trova sulla linea della loro intersezione.

Sostituiamo le coordinate del punto N 0 (0, - 1 3, 1) in entrambe le equazioni del piano. Otteniamo 2 0 + 3 - 1 3 + 1 = 0 0 - 2 - 1 3 + 1 - 3 = 0 ⇔ 0 = 0 - 1 1 3 = 0 .

Come puoi vedere, la seconda equazione del sistema si è trasformata in un'uguaglianza errata. Ciò significa che il punto N 0 non appartiene alla retta data.

Risposta: il punto M 0 appartiene a una retta e il punto N 0 no.

Ora ti offriamo un algoritmo per trovare le coordinate di un certo punto appartenente a una retta, se la retta nello spazio in un sistema di coordinate rettangolare O xyz è determinata dalle equazioni dei piani intersecanti A 1 x + B 1 y + C 1 z + D 1 = 0 UN 2 x + B 2 y + C 2 z + D 2 = 0 .

Il numero di soluzioni di un sistema di due equazioni lineari con incognite A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 è infinito. Ognuna di queste soluzioni può essere una soluzione al problema.

Facciamo un esempio.

Esempio 3

Sia data una retta nello spazio tridimensionale dalle equazioni di due piani intersecanti della forma x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 . Trova le coordinate di uno qualsiasi dei punti su questa linea.

Soluzione

Riscriviamo il sistema di equazioni x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 ⇔ x + 0 y + 3 z = - 7 2 x + 3 y + 3 z = - 2 .

Prendiamo come base minore della matrice principale del sistema un minore del secondo ordine diverso da zero 1 0 2 3 = 3 ≠ 0 . Significa che z è una variabile sconosciuta libera.

Trasferiamo i termini contenenti la variabile incognita libera z ai lati destro delle equazioni:

x + 0 y + 3 z = - 7 2 x + 3 y + 3 z = - 2 ⇔ x + 0 y = - 7 - 3 z 2 x + 3 y = - 2 - 3 z

Introduciamo un numero reale arbitrario λ e assumiamo che z = λ .

Allora x + 0 y = - 7 - 3 z 2 x + 3 y = - 2 - 3 z ⇔ x + 0 y = - 7 - 3 λ 2 x + 3 y = - 2 - 3 λ .

Per risolvere il sistema di equazioni risultante, applichiamo il metodo di Cramer:

∆ = 1 0 2 3 = 1 3 - 0 1 = 2 ∆ x = - 7 - 3 λ 0 - - 3 λ 3 = - 7 - 3 λ 3 - 0 (- 2 - 3 λ) = 21 - 9 λ ⇒ x = ∆ x ∆ = - 7 - 3 λ ∆ y = 1 - 7 - 3 λ 2 - 2 - 3 λ = 1 - 2 - 3 λ - - 7 - 3 λ = 12 + 3 λ ⇒ y = ∆ y ∆ = 4 + λ

La soluzione generale del sistema di equazioni x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 sarà x = - 7 - 3 λ y = 4 + λ z = λ , dove λ ∈ R .

Per ottenere una soluzione particolare del sistema di equazioni, che ci dia le coordinate desiderate di un punto appartenente ad una determinata retta, dobbiamo prendere un valore specifico del parametro λ. Se λ = 0 , allora x = - 7 - 3 0 y = 4 + 0 z = 0 ⇔ x = - 7 y = 4 z = 0 .

Questo ci permette di ottenere le coordinate del punto desiderato - 7, 4, 0.

Verifichiamo la correttezza delle coordinate trovate del punto sostituendole nelle equazioni iniziali di due piani intersecanti - 7 + 3 0 + 7 = 0 2 (- 7) + 3 4 + 3 0 + 2 = 0 ⇔ 0 = 0 0 = 0.

Risposta: - 7 , 4 , 0

Vettore di direzione di una linea lungo la quale due piani si intersecano

Diamo un'occhiata a come determinare le coordinate del vettore di direzione di una retta, che è data dalle equazioni di due piani intersecanti A 1 x + B 1 y + C 1 z + D 1 = 0 e A 2 x + B 2 y + C 2 z + D 2 = 0 . In un sistema di coordinate rettangolare 0xz, il vettore diretto di una retta è inseparabile da una retta.

Come sappiamo, una retta è perpendicolare a un piano se è perpendicolare a qualsiasi retta giacente nel piano dato. Sulla base di quanto sopra, il vettore normale del piano è perpendicolare a qualsiasi vettore diverso da zero che giace nel piano dato. Questi due fatti ci aiuteranno a trovare il vettore di direzione della retta.

I piani α e β si intersecano lungo la linea un . Vettore di direzione a → retta un è perpendicolare al vettore normale n 1 → = (A 1 , B 1 , C 1) del piano A 1 x + B 1 y + C 1 z + D 1 = 0 e al vettore normale n 2 → = (A 2 , B 2 , C 2) piani A 2 x + B 2 y + C 2 z + D 2 = 0 .

Direzione vettore dritto un è un prodotto vettoriale di vettori n → 1 = (A 1 , B 1 , C 1) e n 2 → = A 2 , B 2 , C 2 .

a → = n → 1 × n 2 → = io → j → k → A 1 B 1 C 1 A 2 B 2 C 2

Definiamo l'insieme di tutti i vettori direttivi della retta come λ · a → = λ · n 1 → × n 2 → , dove λ è un parametro che può assumere qualsiasi valore reale diverso da zero.

Esempio 4

Sia data una retta nello spazio in un sistema di coordinate rettangolare O x y z dalle equazioni di due piani intersecanti x + 2 y - 3 z - 2 = 0 x - z + 4 = 0 . Trova le coordinate di qualsiasi vettore di direzione di questa linea.

Soluzione

I piani x + 2 y - 3 z - 2 = 0 e x - z + 4 = 0 hanno vettori normali n 1 → = 1 , 2 , - 3 e n 2 → = 1 , 0 , - 1 . Prendiamo come vettore diretto una retta, che è l'intersezione di due dati aerei, il prodotto incrociato di vettori normali:

a → = n → 1 × n 2 → = i → j → k → 1 2 - 3 1 0 - 1 = i → 2 (- 1) + j → (- 3) 1 + k → 1 0 - - k → 2 1 - j → 1 (- 1) - io → (- 3) 0 = - 2 io → - 2 j → - 2 k →

Scriviamo la risposta nella forma delle coordinate a → = - 2 , - 2 , - 2 . Per coloro che non ricordano come è fatto, si consiglia di fare riferimento all'argomento "Coordinate vettoriali in un sistema di coordinate rettangolare".

Risposta: a → = - 2 , - 2 , - 2

Transizione alle equazioni parametriche e canoniche di una retta nello spazio

Per risolvere una serie di problemi, è più facile utilizzare equazioni parametriche di una retta nello spazio della forma x = x 1 + ax λ y = y 1 + ay λ z = z 1 + az λ o equazioni canoniche di una retta retta nello spazio della forma x = x 1 + ax λ y = y 1 + ay λ z = z 1 + az λ . In queste equazioni, a x , a y , a z sono le coordinate del vettore di direzione della retta, x 1 , y 1 , z 1 sono le coordinate di un punto sulla retta e λ è un parametro che assume valori reali arbitrari.

Da un'equazione di retta della forma A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0, possiamo passare al canonico e equazioni parametriche retta nello spazio. Per scrivere le equazioni canoniche e parametriche di una retta, abbiamo bisogno delle capacità di trovare le coordinate di un punto della retta, così come le coordinate di alcuni vettori direttivi della retta, dato dalle equazioni due piani intersecanti.

Diamo un'occhiata all'esempio sopra.

Esempio 5

Impostiamo una retta in un sistema di coordinate tridimensionale dalle equazioni di due piani intersecanti 2 x + y - z - 1 = 0 x + 3 y - 2 z = 0 . Scriviamo le equazioni canoniche e parametriche di questa retta.

Soluzione

Trova le coordinate del vettore diretto della retta, che è il prodotto vettoriale dei vettori normali n 1 → = 2 , 1 , - 1 del piano 2 x + y - z - 1 = 0 e n 2 → = (1 , 3 , - 2) del piano x + 3 y-2z=0:

a → = n 1 → × n 2 → = i → j → k → 2 1 - 1 1 3 - 2 = i → 1 (- 2) + j → (- 1) 1 + k → 2 3 - - k → 1 1 - j → 2 (- 2) - io → (- 1) 3 = io → + 3 j → + 5 k →

Coordinate del vettore di direzione della retta a → = (1 , 2 , 5) .

Il passo successivo è determinare le coordinate di un punto della retta data, che è una delle soluzioni del sistema di equazioni: 2 x + y - z - 1 = 0 x + 3 y - 2 z = 0 ⇔ 2 x + y - z = 1 x + 3 y - 2z = 0 .

Prendiamo il determinante 2 1 1 3 = 2 · 3 - 1 · 1 = 5 come matrice minore del sistema, che è diversa da zero. In questo caso, la variabile z è libero. Trasferiamo i termini con esso sul lato destro di ciascuna equazione e diamo alla variabile un valore arbitrario λ:

2 x + y - z = 1 x + 3 y - 2 z = 0 ⇔ 2 x + y = 1 + zx + 3 y = 2 z ⇔ 2 x + y = 1 + λ x + 3 y = 2 λ , λ ∈ R

Applichiamo il metodo Cramer per risolvere il sistema di equazioni risultante:

∆ = 2 1 1 3 = 2 3 - 1 1 = 5 ∆ x = 1 + λ 1 2 λ 3 = (1 + λ) 3 - 1 2 λ = 3 + λ ⇒ x = ∆ x ∆ = 3 + λ 5 = 3 5 + 1 5 λ ∆ y = 2 1 + λ 1 2 λ = 2 2 λ - (1 + λ) 1 = - 1 + 3 λ ⇒ y = ∆ y ∆ = - 1 + 3 λ 5 = - 1 5 + 3 5 λ

Otteniamo: 2 x + y - z - 1 = 0 x + 3 y - 2 z = 0 ⇔ x = 3 5 + 1 5 y = - 1 5 + 3 5 z = λ

Prendiamo λ = 2 per ottenere le coordinate di un punto su una retta: x 1 = 3 5 + 1 5 2 y 1 = - 1 5 + 3 5 2 z 1 = 2 ⇔ x 1 = 1 y 1 = 1z 1 = 2 . Ora abbiamo abbastanza dati per scrivere nello spazio le equazioni canoniche e parametriche di questa retta: x - x 1 ax = y - y 1 ay = z - z 1 az ⇔ x - 1 1 = y - 1 3 = z - 2 5 x = x 1 + ax λ y = y 1 + ay λ z = z 1 + az λ ⇔ x = 1 + 1 λ y = 1 + 3 λ z = 2 + 5 λ ⇔ x = 1 + λ y = 1 + 3 λ z = 2 + 5 λ

Risposta: x - 1 1 = y - 1 3 = z - 2 5 e x = 1 + λ y = 1 + 3 λ z = 2 + 5 λ

Questo problema ha un altro modo per risolverlo.

Trovare le coordinate di un certo punto su una retta si effettua risolvendo il sistema di equazioni A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0.

Nel caso generale, le sue soluzioni possono essere scritte nella forma delle equazioni parametriche desiderate di una retta nello spazio x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ .

L'ottenimento delle equazioni canoniche si effettua come segue: risolviamo ciascuna delle equazioni ottenute rispetto al parametro λ, uguagliamo le parti giuste dell'uguaglianza.

x = x 1 + ax λ y = y 1 + ay λ z = z 1 + az λ ⇔ λ = x - x 1 ax λ = y - y 1 ay λ = z - z 1 az ⇔ x - x 1 ax = y - y 1 ay = z - z 1 az

Applicabile Da questa parte per risolvere il problema.

Esempio 6

Impostiamo la posizione della retta dalle equazioni di due piani intersecanti 2 x + y - z - 1 = 0 x + 3 y - 2 z = 0 . Scriviamo le equazioni parametriche e canoniche per questa retta.

Soluzione

La soluzione di un sistema di due equazioni con tre incognite viene eseguita allo stesso modo dell'esempio precedente. Otteniamo: 2 x + y - z - 1 = 0 x + 3 y - 2 z = 0 ⇔ x = 3 5 + 1 5 λ y = - 1 5 + 3 5 λ z = λ .

Queste sono le equazioni parametriche di una retta nello spazio.

Le equazioni canoniche si ottengono come segue: x = 3 5 + 1 5 λ y = - 1 5 + 3 5 λ z = λ ⇔ λ = x - 3 5 1 5 λ = y + 1 5 3 5 λ = z 1 ⇔ x - 3 5 1 5 = y + 1 5 3 5 = z 1

Le equazioni ottenute in entrambi gli esempi differiscono esternamente, ma sono equivalenti, poiché determinano lo stesso insieme di punti nello spazio tridimensionale, e quindi la stessa retta.

Risposta: x - 3 5 1 5 = y + 1 5 3 5 = z 1 e x = 3 5 + 1 5 λ y = - 1 5 + 3 5 λ z = λ

Se noti un errore nel testo, evidenzialo e premi Ctrl+Invio

Il problema dell'intersezione dei piani, per la sua importanza, è chiamato da diversi autori "problema posizionale n. 2".

Dalla stereometria è noto che la linea di intersezione di due piani è una retta. Nei precedenti problemi preliminari, dove ci siamo occupati di casi particolari di intersezione di piani, siamo partiti da questa definizione.

Come è noto, per costruire l'una o l'altra retta, nel caso più semplice, è necessario trovare due punti appartenenti a tale retta. Nel caso di specificare un piano tramite tracce, questi due punti sono i punti di intersezione delle tracce con lo stesso nome di piani intersecanti.

Esempi di lavoro autonomo

Esercizio 5.1

Costruire linee di intersezione dei piani date da tracce (Fig. 72):

• a) sporgente orizzontalmente I e sporgente frontalmente A;
• b) Z e piano sporgenti orizzontalmente posizione generale Q;
• c) due piani in posizione generale I e 0.

Riso. 72

Sulla fig. 73 mostra le risposte a questo esercizio.

Per i casi in cui i piani sono definiti da figure locali piatte, è opportuno utilizzare almeno due diverse soluzioni.

Riso. 73

La prima soluzione è uso di un algoritmo a tre stadi per trovare il punto di incontro di una retta in posizione generale con un piano in posizione generale. Per trovare la linea di intersezione di due triangoli, uno dei triangoli viene lasciato invariato e il secondo viene diviso mentalmente in segmenti separati, rappresentandoli come linee rette in posizione generale. Innanzitutto, trova il punto di intersezione di una delle rette in posizione generale con il piano del triangolo. Quindi trovano un altro punto mancante appartenente alla linea desiderata. Questo viene fatto in modo simile, ripetendo l'intera sequenza di azioni descritte.

Esercizio 5.2

Secondo le coordinate date dei vertici di due triangoli LAN e DEK costruisci un diagramma di questi ultimi e trova la linea della loro intersezione. Specificare la visibilità degli elementi di entrambi i triangoli sul diagramma: MA(0, 9, 2); ?(10, 1, 16); C (23, 14, 9); D(3, 17, 18); ?(22, 11, 17); ?(12.0, 2). Per trovare le linee di intersezione dei triangoli, si consiglia di trovare prima il punto di incontro della linea KD con un triangolo ABC, e poi il punto di incontro della retta SW con un triangolo EDK.

La vista generale del diagramma risultante è mostrata in fig. 74.

La seconda soluzione è utilizzo di due piani di taglio ausiliari della livella.

Le date figure piatte intersecanti dovrebbero essere attraversate due volte da piani di livello ausiliari (simili o opposti - non importa), ad esempio, da due piani di livello orizzontali.

È facile capire che una dissezione una tantum consente di trovare due linee che si intersecano hl e E 2 , dando un punto MA, appartenente alla linea di intersezione desiderata (Fig. 75). Disegnare un altro piano ausiliario simile a una certa distanza

Riso. 74

Riso. 75

dal primo, ottieni una costruzione simile e un punto in più. Collegando le proiezioni omonime dei due punti ottenuti, trovano la linea di intersezione desiderata dei due piani.

Esercizio 5.3

Secondo le coordinate date dei punti di due figure triangolari, costruisci un diagramma di queste ultime, su cui costruire, utilizzando piani ausiliari, la linea di intersezione dei triangoli. Specificare la visibilità degli elementi di entrambi i triangoli sul diagramma:

all'ABC. MA(16, 5, 17); Io (10, 19,

UN DIF: D (24, 12, 14); ? (4, 18,

La vista generale del problema risolto è mostrata in fig. 76.

Esercizio 5.4

Per consolidare le capacità di trovare la linea di intersezione di due piani, viene fornito un problema la cui soluzione è data nella dinamica delle costruzioni secondo i passaggi dell'algoritmo.

Trova la linea di intersezione di due piani di posizione comune R IS jq

linee definite da due triangoli ABC e DEF, e determinare la visibilità della loro compenetrazione (Fig. 77).

La soluzione dell'esempio si riduce a trovare i punti di intersezione dei lati (linee rette) A ABC con un piano generico dato da A DEF. L'algoritmo per risolvere questo esempio è noto.

Concludiamo il lato (dritto) LAN AC nel piano ausiliario a sbalzo frontale t _1_ P 2 (Fig. 78).

La traccia frontale di questo piano ausiliario interseca le sporgenze dei lati D 2 E 2 GLE 2 - 1 2 e D 2 F 2 pt 2 = 2 2 ai punti 1 2 e 2 2 . Le linee di comunicazione di proiezione consentono di determinare la linea di intersezione sul piano di proiezione orizzontale (1 !~2 2) = n A D X E X F ( . Poi il punto K 1 e la sua proiezione K 2 determinare il punto di intersezione della retta corrente alternata con un DEF.

Ripetiamo l'algoritmo per trovare il punto di intersezione del lato A ABC dritto sole con ADEF. Concludiamo il velivolo in un piano ausiliario a proiezione frontale p _L P 2 (Fig. 79).

Troviamo le proiezioni dei punti 3 e 4 e sul piano orizzontale delle proiezioni determiniamo la proiezione del punto di intersezione della retta In 1 C [ con la linea di intersezione (3,-4,):

La linea di comunicazione di proiezione permette di trovare il suo punto di proiezione frontale M2.

Colleghiamo i punti trovati Ki Mi trova la linea di intersezione di due piani in posizione generale A ABC n / A DIF= AF (fig. 80).

Visibilità laterale ABC relativamente ADEF determinato dai punti in competizione. Per prima cosa determinare la visibilità forme geometriche sul piano delle proiezioni П 2 . Per fare ciò, attraverso i punti 5 e 6 in competizione (5 2 = 6 2) tracciamo una linea di comunicazione di proiezione perpendicolare all'asse di proiezione x n(Fig. 81).

Su proiezioni orizzontali 5 U e 6 { punti 5 e 6, in cui la linea del raccordo di proiezione, rispettivamente, interseca le rette intersecanti corrente alternata 4 DF, risulta che il punto 6 è più distante dal piano di proiezione P 2 del punto 5. Pertanto, il punto 6 e la retta DF, a cui appartiene sono visibili rispetto al piano delle proiezioni P 2 . Ne consegue che il segmento (K 2 -6 2) sarà invisibile. Allo stesso modo, determiniamo la visibilità dei lati A LAN e A DEF - Dom e DF, quelli. il segmento (W 2 -8 2) sarà invisibile.

Visibilità ABC e ADEF rispetto al piano delle proiezioni П j, è stabilito in modo simile. Per determinare la visibilità delle linee di intersezione AC * DF e BC ±DF rispetto al piano delle proiezioni P] attraverso punti concorrenti 9 1 = 10 1 e 11 1 = 12 1 tracciamo linee di comunicazione di proiezione perpendicolarmente x pag. Sulla base delle proiezioni frontali di questi punti concorrenti, stabiliamo che le proiezioni dei punti 10 2 e 12 2 sono più distanti dal piano di proiezione P ( . Di conseguenza, i segmenti (A^-YUD e (M g 2 1) sarà invisibile. Da qui la visibilità ABC e ADEF chiaramente mostrato in Fig. 82.

ANGOLO TRA I PIANI

Consideriamo due piani α 1 e α 2 dati rispettivamente dalle equazioni:

Sotto angolo tra due piani si intende uno degli angoli diedri formati da questi piani. È ovvio che l'angolo tra i vettori normali ed i piani α 1 e α 2 è uguale ad uno degli angoli diedri adiacenti indicati o . Ecco perché . Perché e , poi

.

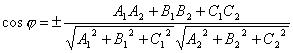Esempio. Determina l'angolo tra i piani X+2y-3z+4=0 e 2 X+3y+z+8=0.

Condizione di parallelismo di due piani.

Due piani α 1 e α 2 sono paralleli se e solo se i loro vettori normali e sono paralleli, e quindi .

Quindi, due piani sono paralleli tra loro se e solo se i coefficienti alle coordinate corrispondenti sono proporzionali:

o

Condizione di perpendicolarità dei piani.

È chiaro che due piani sono perpendicolari se e solo se i loro vettori normali sono perpendicolari, e quindi, o .

In questo modo, .

Esempi.

DIRETTA NELLO SPAZIO.

EQUAZIONE VETTORIALE DIRETTA.

EQUAZIONI PARAMETRICHE DIRETTE

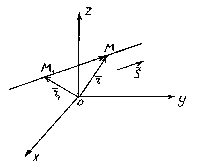
La posizione di una retta nello spazio è completamente determinata specificando uno qualsiasi dei suoi punti fissi m 1 e un vettore parallelo a questa retta.

Viene chiamato un vettore parallelo a una retta guida il vettore di questa linea.

Quindi andiamo dritto l passa per un punto m 1 (X 1 , y 1 , z 1) giacente su una retta parallela al vettore.

Considera un punto arbitrario M(x,y,z) su una linea retta. Si può vedere dalla figura che .

I vettori e sono collineari, quindi esiste un tale numero T, cosa , dov'è il moltiplicatore T può assumere qualsiasi valore numerico a seconda della posizione del punto m su una linea retta. Fattore Tè chiamato parametro. Indicazione dei vettori raggio dei punti m 1 e m rispettivamente, attraverso e , otteniamo . Questa equazione è chiamata vettore equazione di linea retta. Mostra che ogni valore di parametro T corrisponde al vettore raggio di un punto m sdraiato su una linea retta.

Scriviamo questa equazione in forma di coordinate. Notare che , e da qui

Le equazioni risultanti sono chiamate parametrico equazioni in linea retta.

Quando si modifica il parametro T cambiano le coordinate X, y e z e punto m si muove in linea retta.

EQUAZIONI CANONICHE DIRETTE

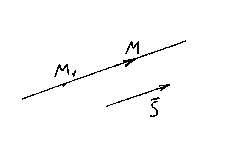
Lascia stare m 1 (X 1 , y 1 , z 1) - un punto che giace su una linea retta l, E è il suo vettore di direzione. Ancora una volta, prendi un punto arbitrario su una linea retta M(x,y,z) e considera il vettore.

È chiaro che i vettori e sono collineari, quindi le rispettive coordinate devono essere proporzionali, quindi

– canonico equazioni in linea retta.

Nota 1. Si noti che le equazioni canoniche della retta possono essere ottenute dalle equazioni parametriche eliminando il parametro T. Infatti, dalle equazioni parametriche otteniamo o .

Esempio. Scrivi l'equazione di una retta in modo parametrico.

Denota , quindi X = 2 + 3T, y = –1 + 2T, z = 1 –T.

Nota 2. Lascia che la linea sia perpendicolare a uno di assi coordinati, come l'asse Bue. Allora il vettore di direzione della retta è perpendicolare Bue, Di conseguenza, m=0. Di conseguenza, le equazioni parametriche della retta prendono la forma

Eliminazione del parametro dalle equazioni T, otteniamo le equazioni della retta nella forma

Tuttavia, anche in questo caso, accettiamo di scrivere formalmente le equazioni canoniche della retta nella forma . Pertanto, se il denominatore di una delle frazioni è zero, significa che la linea è perpendicolare all'asse delle coordinate corrispondente.

Allo stesso modo, le equazioni canoniche corrisponde ad una retta perpendicolare agli assi Bue e Ehi o asse parallelo Oz.

Esempi.

EQUAZIONI GENERALI UNA LINEA DIRETTA COME LINEA DI INTERCETTAZIONE DI DUE AEREI

Per ogni retta nello spazio passa un numero infinito di piani. Due di loro, intersecantisi, lo definiscono nello spazio. Pertanto, le equazioni di due piani qualsiasi, considerati insieme, sono le equazioni di questa retta.

In generale, due piani non paralleli qualsiasi dati dalle equazioni generali

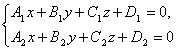
determinare la loro linea di intersezione. Queste equazioni sono chiamate equazioni generali dritto.

Esempi.

Costruisci una retta data da equazioni

Per costruire una retta basta trovare due dei suoi punti. Il modo più semplice è scegliere i punti di intersezione della linea con piani coordinati. Ad esempio, il punto di intersezione con il piano xOy otteniamo dalle equazioni di una retta, assumendo z= 0:

Risolvendo questo sistema, troviamo il punto m 1 (1;2;0).

Allo stesso modo, supponendo y= 0, otteniamo il punto di intersezione della retta con il piano xOz:

Dalle equazioni generali di una retta si può procedere alle sue equazioni canoniche o parametriche. Per fare questo, devi trovare un punto m 1 sulla retta e il vettore di direzione della retta.

Coordinate del punto m 1 otteniamo da questo sistema di equazioni, dando a una delle coordinate un valore arbitrario. Per trovare il vettore di direzione, si noti che questo vettore deve essere perpendicolare a entrambi i vettori normali e . Pertanto, per il vettore di direzione della retta l puoi prendere il prodotto incrociato di vettori normali:

.

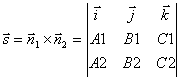Esempio. Fornisci le equazioni generali della retta alla forma canonica.

Trova un punto su una retta. Per fare ciò, scegliamo arbitrariamente una delle coordinate, ad esempio, y= 0 e risolvi il sistema di equazioni:

I vettori normali dei piani che definiscono la linea hanno coordinate Pertanto, il vettore di direzione sarà dritto

. Di conseguenza, l: .

ANGOLO TRA DIRITTI

angolo tra rette nello spazio chiameremo uno qualsiasi degli angoli adiacenti formati da due rette tracciate attraverso un punto arbitrario parallelo ai dati.

Siano date due rette nello spazio:

Ovviamente, l'angolo φ tra le linee può essere preso come l'angolo tra i loro vettori di direzione e . Poiché , quindi secondo la formula per il coseno dell'angolo tra i vettori otteniamo