DOPPI INTEGRALI

CONFERENZA 1

Integrali doppi.Definizione dell'integrale doppio e sue proprietà. Integrali iterati. Riduzione degli integrali doppi a quelli ripetuti. Disposizione dei limiti di integrazione. Calcolo di integrali doppi in sistema cartesiano coordinate.

L'integrale doppio è una generalizzazione del concetto integrale definito nel caso di una funzione di due variabili. In questo caso, invece di un segmento di integrazione, ci sarà una specie di figura piatta.

Permettere Dè un dominio limitato chiuso, e f(x,y) è una funzione arbitraria definita e limitata in questo dominio. Assumiamo che i confini della regione D costituito da un numero finito di curve, dato dalle equazioni tipo y=f(X) o X=g( y), dove f(X) e g(y) sono funzioni continue.

Dividiamo l'area D a caso n parti. Piazza io il segmento è indicato dal simbolo D s io. Su ogni sezione, scegliamo arbitrariamente un punto Pi, e lascia che abbia coordinate in un sistema cartesiano fisso ( x io, y io). Componiamo somma integrale per funzione f(x,y) per zona D, per fare ciò, troviamo i valori della funzione in tutti i punti Pi, li moltiplichiamo per le aree dei segmenti corrispondenti Ds io e riassumi tutti i risultati:

Chiamiamo diam(G) la zona G la distanza maggiore tra i punti di confine di quest'area.

doppio integrale funzioni f(x,y) nel dominio D è il limite a cui tende la successione delle somme integrali (1.1) con aumento illimitato del numero delle partizioni n (in cui). Questo è scritto come segue

Si noti che, in generale, la somma integrale per data funzione e l'area di integrazione data dipende dal metodo di partizione dell'area D e selezione dei punti Pi. Tuttavia, se esiste l'integrale doppio, significa che il limite delle somme integrali corrispondenti non dipende più da questi fattori. Affinché l'integrale doppio esista(o, come si suol dire, in modo che la funzione f(x,y) è integrabile nel dominio D), è sufficiente che l'integrando sia continuo nella data area di integrazione.

Lascia che la funzione f(x,y) è integrabile nel dominio D. Poiché il limite delle somme integrali corrispondenti per tali funzioni non dipende dal metodo di partizionamento del dominio di integrazione, il partizionamento può essere eseguito utilizzando linee verticali e orizzontali. Poi la maggior parte della regione D avrà una forma rettangolare, la cui area è uguale a D s io=D x io D si io. Pertanto, il differenziale di area può essere scritto come ds=dxdy. Di conseguenza, in coordinate cartesiane, integrali doppi può essere scritto nel modulo

Commento. Se l'integrando f(x,y)º1, quindi il doppio integrale sarà uguale all'area della regione di integrazione:

Si noti che gli integrali doppi hanno le stesse proprietà degli integrali definiti. Segnaliamo alcuni di loro.

Proprietà degli integrali doppi.

1 0 . Proprietà lineare. L'integrale della somma delle funzioni è uguale alla somma degli integrali:

e il fattore costante può essere estratto dal segno di integrale:

2 0 .Proprietà additiva. Se il dominio di integrazione D è diviso in due parti, il doppio integrale sarà uguale alla somma degli integrali su ciascuna parte:

3 0 .Il teorema del valore medio. Se la funzione f( x,y)è continua nel dominio D, quindi in questo dominio c'è un punto del genere(x,h) , che cosa:

Allora sorge la domanda: come si calcolano gli integrali doppi? Può essere calcolato approssimativamente, per questo scopo è sviluppato metodi efficaci compilando le corrispondenti somme integrali, che vengono poi calcolate numericamente utilizzando un computer. Nel calcolo analitico degli integrali doppi, sono ridotti a due integrali definiti.

Proprietà degli integrali doppi.

Alcune delle proprietà degli integrali doppi derivano direttamente dalla definizione di questo concetto e dalle proprietà delle somme integrali, vale a dire:

1. Se funzione f(x, y) integrabile in D, poi kf(x, y)è integrabile anche in questa regione, e (24.4)

2. Se in zona D funzioni integrabili f(x, y) e g(x, y), quindi le funzioni f(x, y) ± g(x, y), e dove

3. Se per integrabile nel dominio D funzioni f(x, y) e g(x, y) la disuguaglianza f(x, y)≤g(x, y), poi

(24.6)

Dimostriamo altre proprietà dell'integrale doppio:

4. Se zona D divisa in due aree D 1 e D 2 senza punti interni comuni e funzione f(x, y) continuo nella regione D, poi

(24.7) Prova . Somma integrale sull'area D può essere rappresentato come:

dov'è la partizione dell'area D disegnato in modo che il confine tra D 1 e D 2 è costituito dai confini di parti della partizione. Passando quindi al limite in , otteniamo l'uguaglianza (24.7).

5. Nel caso di integrabilità su D funzioni f(x, y) in questa regione anche la funzione è integrabile | f(x, y) |, e la disuguaglianza

(24.8)

Prova.

da cui, passando al limite come , otteniamo la disuguaglianza (24.8)

6. dove S D– zona della regione D. La prova di questa affermazione si ottiene sostituendo nella somma integrale f(x, y)≡ 0.

7. Se integrabile nella regione D funzione f(x, y) soddisfa la disuguaglianza

m ≤ f(x, y) ≤ M,

poi (24.9)

Prova.

La dimostrazione si effettua passando al limite dalla disuguaglianza evidente

Conseguenza.

Se dividiamo tutte le parti della disuguaglianza (24.9) per D, possiamo ottenere il cosiddetto teorema del valore medio:

In particolare, a condizione di continuità della funzione f in D c'è un punto del genere in questa regione ( x 0, y 0), in cui f(x 0, y 0) = μ , questo è

-

Un'altra formulazione del teorema del valore medio.

Il significato geometrico dell'integrale doppio.

Considera un corpo V, delimitata da una parte della superficie data dall'equazione z = f(x, y), proiezione D questa superficie al piano O eh e una superficie cilindrica laterale ottenuta da generatori verticali che collegano i punti di confine della superficie con le loro sporgenze.

z=f(x,y)

V

y P i D Fig.2.

Cercheremo il volume di questo corpo come limite della somma dei volumi dei cilindri le cui basi sono le parti Δ si le zone D e le altezze sono segmenti con lunghezze f(Pi), dove i punti Pi appartengono a Δ si. Passando al limite a , otteniamo quello

(24.11)

cioè il doppio integrale è il volume del cosiddetto cilindroide delimitato dall'alto dalla superficie z = f(x, y), e sotto - l'area D.

Calcolo di un integrale doppio riducendolo a uno iterato.

Considera la zona D delimitato da linee x=a, x=b(un< b ), dove φ 1 ( X) e φ 2 ( X) sono continui su [ a, b]. Quindi qualsiasi linea parallela all'asse delle coordinate O a e passando per il punto interno della regione D, attraversa il confine della regione in due punti: N 1 e N 2 (Fig. 1). Chiamiamo quest'area corretta in su-

a Regola dell'asse O a. Allo stesso modo, il

y=φ 2 (X) c'è un'area corretta nella direzione

N 2 assi O X. L'area corretta nella direzione

Tutti e due assi coordinati, noi

D chiamalo giusto. Per esempio,

l'area corretta è mostrata in Fig.1.

y=φ 1 (X) N 1

O a b x

Lascia che la funzione f(x, y) continuo nella regione D. Considera l'espressione

, (24.12)

chiamato doppio integrale dalla funzione f(x, y) per regione D. Calcoliamo prima l'integrale interno (tra parentesi) sulla variabile a conteggio X permanente. Il risultato sarà funzione continua da X:

Integriamo la funzione risultante sopra X che vanno da un prima b. Di conseguenza, otteniamo il numero

Dimostriamo un'importante proprietà dell'integrale doppio.

Teorema 1. Se la zona D, correggere nella direzione O a, divisa in due regioni D 1 e D 2 rettilineo, parallelo all'asse O a o asse O X, quindi l'integrale doppio sulla regione D sarà uguale alla somma degli stessi integrali sulle regioni D 1 e D 2:

Prova.

a) Lascia la linea x = c pause D sul D 1 e D 2, correggere in direzione O a. Quindi

+

+

b) Lascia la linea y=h pause D a destra in direzione di O a le zone D 1 e D 2 (Fig. 2). Indica con M 1 (un 1 , h) e M 2 (b 1 , h) punti di intersezione della retta y=h con bordo l le zone D.

y Regione D 1 delimitata da linee continue

y=φ 2 (X) 1) y=φ 1 (X);

D 2 2) curva MA 1 M 1 M 2 A, di cui scriviamo l'equazione

h M 1 M 2 y=φ 1 *(X), dove φ 1 *(X) = φ 2 (X) a a ≤ x ≤ a 1 e

UN 1 D 1 Bb 1 ≤ x ≤ b, φ 1 *(X) = h a un 1 ≤ x ≤ b 1 ;

3) dritto x = a, x = b.

Regione D 2 limitato da righe y=φ 1 *(X),

Ay= φ 2 (X),un 1 ≤ x ≤ b 1 .

y=φ 1 (X) Applichiamo il teorema all'integrale interno

suddividendo l'intervallo di integrazione:

oh un a 1 b 1 b

+

Rappresentiamo il secondo degli integrali ottenuti come somma:

+ + .

Perché il φ 1 *(X) = φ 2 (X) a a ≤ x ≤ a 1 e b 1 ≤ x ≤ b, il primo e il terzo integrale ottenuti sono identicamente uguali a zero. Di conseguenza,

io D = , questo è .

Integrali doppi per manichini

Questa lezione introduce l'ampio argomento degli integrali multipli che gli studenti in genere incontrano nel secondo anno. doppio e integrali tripli puoi intimidire il profano non peggio di equazioni differenziali, quindi affronteremo subito la domanda: è difficile o no? Certo, per alcuni sarà difficile e, a dire il vero, sono stato un po' furbo con il titolo dell'articolo: per imparare a risolvere i doppi integrali, devi avere alcune abilità. In primo luogo, se stiamo parlando di integrali, allora, ovviamente, dobbiamo integrare. Logicamente. Pertanto, per padroneggiare gli esempi, devi essere in grado di trovare integrali indefiniti e calcola integrali definiti almeno a livello medio. La buona notizia è che gli integrali stessi sono abbastanza semplici nella maggior parte dei casi.

Chi deve essere duro? È comprensibile. Coloro che hanno bevuto molta birra durante i primi semestri. Tuttavia, rassicurerò anche gli studenti normali: il sito ha tutto il materiale per colmare le lacune o le incomprensioni. Devi solo dedicare più tempo. I collegamenti ad argomenti che dovrebbero essere studiati o ripetuti saranno allegati in tutto l'articolo.

Sul lezione introduttiva I seguenti punti fondamentali verranno analizzati passo dopo passo e in dettaglio:

– Il concetto di integrale doppio

– Area di integrazione. L'ordine di aggirare la regione di integrazione. Come modificare l'ordine di attraversamento?

Dopo aver compreso BENE tutte le nozioni di base, puoi procedere all'articolo Come calcolare l'integrale doppio? Esempi di soluzioni. Inoltre, c'è un problema comune su calcolo dell'integrale doppio in coordinate polari e una tipica applicazione su trovare il baricentro di una figura delimitata piatta.

Cominciamo con una domanda fondamentale: che cos'è?

Il concetto di integrale doppio

Doppio integrale in vista generaleè scritto come segue:

Comprendiamo i termini e la notazione:
– icona doppia integrale;
– area di integrazione (figura piatta);
- l'integrando di due variabili, spesso è abbastanza semplice;
- Icone differenziali.

Cosa significa calcolare un integrale doppio?

Calcolo della doppia media integrale trova NUMERO. Numero più comune:

Ed è altamente desiderabile trovarlo correttamente =)

Il risultato (numero) può essere negativo. E anche zero può facilmente risultare. Mi sono fermato in modo specifico a questo punto, dal momento che molti studenti provano ansia quando la risposta si rivela essere "qualcosa di strano".

Molte persone lo ricordano "ordinario" integrale definitoè anche un numero. È lo stesso qui. Il doppio integrale ha anche un eccellente significato geometrico, ma ne parleremo più avanti, ogni cosa ha il suo tempo.

Come calcolare l'integrale doppio?

Per calcolare l'integrale doppio, lo si deve ridurre al cosiddetto integrali iterati. Si può fare due strade. Il modo più comune è:

Al posto dei punti interrogativi, è necessario porre i limiti dell'integrazione. Inoltre, i singoli punti interrogativi dell'integrale esterno sono numeri, e i doppi punti interrogativi dell'integrale interno sono funzioni una variabile dipendente da "x".

Dove trovare i limiti dell'integrazione? Dipendono da quale area è data nella condizione del problema. L'area è una figura piatta regolare che hai incontrato molte volte, ad esempio, quando calcolare l'area di una figura piana o calcolare il volume di un corpo di rivoluzione. Molto presto imparerai come impostare correttamente i limiti dell'integrazione.

Dopo aver eseguito il passaggio agli integrali iterati, i calcoli seguono direttamente: prima viene preso l'integrale interno, quindi quello esterno. Uno dopo l'altro. Da qui il nome: integrali iterati.

In parole povere, il problema si riduce al calcolo di due integrali definiti. Come puoi vedere, non tutto è così difficile e spaventoso, e se hai imparato l'integrale definito "ordinario", cosa ti impedisce di affrontare due integrali?!

Il secondo modo per passare agli integrali iterati è un po' meno comune:

Cosa è cambiato? L'ordine di integrazione è cambiato: ora l'integrale interno è preso su "x" e quello esterno su "y". I limiti di integrazione, indicati da asterischi - sarà diverso! Le singole stelle dell'integrale esterno sono numeri, e le doppie stelle dell'integrale interno sono funzioni inverse a seconda di "y".

In qualunque modo scegliamo di passare agli integrali iterati, la risposta finale è destinata ad essere la stessa:

Per favore, ricorda questa importante proprietà, che può essere utilizzato, tra l'altro, per verificare la soluzione.

Algoritmo per risolvere l'integrale doppio:

Sistemiamo le informazioni: in quale ordine dovrebbe essere risolto il problema in esame?

1) È necessario completare il disegno. Senza un disegno, il problema non può essere risolto. Più precisamente, decide di decidere, ma sarà come giocare a scacchi alla cieca. Il disegno dovrebbe rappresentare l'area, che è una figura piatta. Molto spesso, la figura è semplice e limitata ad alcune linee rette, parabole, iperboli, ecc. Durante le lezioni si può padroneggiare una tecnica competente e veloce per la costruzione dei disegni Grafici e proprietà di base delle funzioni elementari, Trasformazioni di grafici geometrici. Quindi, il primo passo è completare il disegno.

2) Imposta i limiti di integrazione e vai agli integrali iterati.

3) Prendi l'integrale interno

4) Prendi l'integrale esterno e ottieni la risposta (numero).

Regione di integrazione. L'ordine di aggirare la regione di integrazione.
Come modificare l'ordine di attraversamento?

In questa sezione considereremo la domanda più importante: come passare agli integrali iterati e impostare correttamente i limiti dell'integrazione. Come accennato in precedenza, puoi farlo in questo modo:

Così:

In pratica, questo compito apparentemente semplice causa le maggiori difficoltà e spesso gli studenti si confondono nel fissare i limiti dell'integrazione. Considera un esempio specifico:

Esempio 1

Soluzione: Descriviamo l'area di integrazione nel disegno:

La solita figura piatta e niente di speciale.

Ora darò a ciascuno di voi uno strumento: un bastone da scavo, un puntatore laser. Il compito è scansionare ogni punto dell'area ombreggiata con un raggio laser:

Il raggio laser attraversa la regione di integrazione rigorosamente dal basso verso l'alto, ovvero tieni SEMPRE un puntatore sotto figura piatta. Il raggio entra nella regione attraverso l'asse x, dato dall'equazione, ed esce dalla regione attraverso una parabola (freccia rossa). Per illuminare l'intera area, è necessario rigorosamente da sinistra a destra trascinare il puntatore lungo l'asse da 0 a 1 (freccia verde).

Allora, cos'è successo:
"y" cambia da 0 a ;
"x" cambia da 0 a 1.

Nei compiti, quanto sopra è scritto sotto forma di disuguaglianze:

Queste disuguaglianze sono chiamate bypass del dominio di integrazione o semplicemente ordine di integrazione

Dopo aver calcolato l'ordine di attraversamento, possiamo passare dall'integrale doppio agli integrali iterati:

La metà del problema è risolto. Ora dobbiamo passare agli integrali iterati nel secondo modo. Per fare ciò, devi trovare le funzioni inverse. Chi ha letto il secondo paragrafo della lezione Volume di un corpo di rivoluzione, sarà più facile. Esaminiamo le funzioni che impostano l'area . Se è abbastanza semplice, vai alle funzioni inverse, il che significa esprimere "x" tramite "y". L'unica funzione dove c'è e "x" e "y", è .

Se , allora e:
la funzione inversa definisce il ramo destro della parabola;
la funzione inversa definisce il ramo sinistro della parabola.

Sorgono spesso dubbi, ad esempio, la funzione determina il ramo sinistro o destro della parabola? È molto facile dissipare i dubbi: prendi un punto della parabola, ad esempio, (dal ramo destro) e sostituisci le sue coordinate in qualsiasi equazione, ad esempio, nella stessa equazione:

Si ottiene l'uguaglianza corretta, il che significa che la funzione determina esattamente il ramo destro della parabola e non il sinistro.

Inoltre, questo controllo(mentalmente o in bozza) è desiderabile effettuare sempre, dopo essere passati alle funzioni inverse. Non ci vorrà proprio niente, ma ti salverà dagli errori di sicuro!

Aggiriamo la regione di integrazione nel secondo modo:

Ora tieni il puntatore laser sinistra dall'area di integrazione. Il raggio laser attraversa l'area rigorosamente da sinistra a destra. In questo caso entra nella regione attraverso un ramo della parabola ed esce dalla regione attraverso la retta data dall'equazione (freccia rossa). Per scansionare l'intera area con un laser, è necessario disegnare un puntatore lungo l'asse rigorosamente dal basso verso l'alto da 0 a 1 (freccia verde).

In questo modo:
"x" cambia da 1;
"y" cambia da 0 a 1.

L'ordine di aggirare l'area dovrebbe essere scritto sotto forma di disuguaglianze:

E, quindi, il passaggio agli integrali iterati è il seguente:

Risposta può essere scritto come segue:

Ancora una volta vi ricordo che il risultato finale dei calcoli non dipende dall'ordine di attraversamento dell'area che abbiamo scelto (ecco perché mettiamo il segno di uguale). Ma prima risultato finale ancora lontano, ora il nostro compito è solo quello di fissare correttamente i limiti dell'integrazione.

Esempio 2

Dato un integrale doppio con il dominio di integrazione. Vai agli integrali iterati e imposta i limiti dell'integrazione in due modi.

Questo è un esempio per soluzione indipendente. Costruisci correttamente un disegno e seguire rigorosamente le indicazioni(da dove e dove brillare con un puntatore laser). Un esempio approssimativo di finitura alla fine della lezione.

Più spesso compito tipico si presenta in una forma leggermente diversa:

Esempio 3

Costruire la regione di integrazione e

Soluzione: Per condizione, viene fornito il primo modo per aggirare la regione. La soluzione inizia di nuovo con un disegno. Qui l'area non giace su un piatto d'argento, ma non è difficile costruirla. Innanzitutto, “togliamo” le funzioni dai limiti di integrazione: , . La funzione, ovviamente, definisce una retta, ma cosa definisce la funzione? Trasformiamolo un po':
- un cerchio con centro all'origine delle coordinate di raggio 2. La funzione definisce il semicerchio superiore (non dimenticare che in caso di dubbio puoi sempre sostituire un punto che giace sul semicerchio superiore o inferiore).

Osserviamo i limiti dell'integrale esterno: "x" cambia da -2 a 0.

Eseguiamo il disegno:

Per chiarezza, ho indicato con le frecce il primo modo per bypassare la regione, che corrisponde agli integrali iterati della condizione: .

Ora dobbiamo cambiare l'ordine di bypass dell'area, per questo procederemo alle funzioni inverse (esprimiamo da "x" a "y"):

Abbiamo recentemente convertito la funzione nell'equazione di un cerchio, quindi esprimiamo "x":
Di conseguenza, otteniamo due funzioni inverse:
- definisce il semicerchio destro;
- definisce il semicerchio sinistro.
Di nuovo, in caso di dubbio, prendi un punto qualsiasi del cerchio e scopri quale è sinistro e quale è giusto.

Cambiamo l'ordine di attraversamento dell'area:

Secondo il secondo metodo di bypass, il raggio laser incluso alla regione sinistra attraverso il semicerchio sinistro e esce a destra attraverso la linea (freccia rossa). Allo stesso tempo, il puntatore laser viene disegnato lungo l'asse y verso l'alto da 0 a 2 (freccia verde).

Pertanto, l'ordine di attraversamento dell'area è:

In generale si può scrivere Rispondere:

Esempio 4

Questo è un esempio fai da te. L'esempio non è molto complicato, ma si noti che l'ordine di attraversamento è inizialmente impostato nel secondo modo! Cosa fare in questi casi? In primo luogo, c'è una difficoltà con il disegno, poiché disegnare un grafico della funzione inversa è insolito anche per me. Raccomando la procedura seguente: in primo luogo, otteniamo una funzione "normale" da (esprimiamo da "y" a "x"). Successivamente, costruiamo un grafico di questa funzione "ordinaria" (puoi sempre costruire almeno in modo puntuale). Facciamo lo stesso con il più semplice funzione lineare: da esprimiamo "y" e tracciamo una linea retta.

Analizziamo i limiti iniziali dell'integrazione: entriamo nella regione da sinistra e usciamo da . Allo stesso tempo, tutte le cose si svolgono nella fascia "di gioco" da -1 a 0. Dopo aver determinato l'area di integrazione sul disegno, non sarà difficile modificare l'ordine del bypass. Un esempio di soluzione alla fine della lezione.

Un esempio simile sarà discusso più dettagliatamente un po' più avanti.

Anche se capisci tutto perfettamente, per favore non affrettarti ad andare direttamente al calcolo del doppio integrale. L'ordine di attraversamento è una cosa complicata, ed è molto importante mettere un po' di mano su questo compito, soprattutto perché non ho ancora coperto tutto!

Nei quattro esempi precedenti, l'area di integrazione era interamente nel 1°, 2°, 3° e 4° quartiere di coordinate. È sempre così? No, naturalmente.

Esempio 5

Modificare l'ordine di integrazione

Soluzione: Eseguiamo il disegno, mentre il grafico della funzione è in realtà una parabola cubica, semplicemente "giace su un lato":

Ordine di attraversamento della regione che corrisponde agli integrali iterati , indicato dalle frecce. Si noti che durante l'esecuzione del disegno è stata disegnata un'altra figura limitata (a sinistra dell'asse y). Pertanto, si dovrebbe fare attenzione quando si determina l'area di integrazione: la cifra sbagliata può essere scambiata per l'area.

Passiamo alle funzioni inverse:
- il ramo destro della parabola di cui abbiamo bisogno;

Cambiamo l'ordine di attraversamento dell'area. Come ricorderete, nel secondo metodo di bypass, l'area deve essere scansionata con un raggio laser da sinistra a destra. Ma ecco una cosa interessante:

Come agire in questi casi? In questi casi, si dovrebbe dividere l'area di integrazione in due parti e per ciascuna delle parti comporre i propri integrali iterati:

1) Se “y” cambia da –1 a 0 (freccia verde), allora il raggio entra nella regione attraverso una parabola cubica ed esce attraverso una linea retta (freccia rossa). Pertanto, l'ordine di attraversamento dell'area sarà il seguente:

2) Se "y" cambia da 0 a 1 (freccia marrone), il raggio entra nella regione attraverso un ramo della parabola ed esce attraverso la stessa retta (freccia cremisi). Pertanto, l'ordine di attraversamento dell'area sarà il seguente:

E i corrispondenti integrali iterati:

Integrali definiti e multipli hanno una proprietà molto conveniente additività, cioè possono essere aggiunti, cosa che in questo caso dovrebbe essere fatta:
- ed ecco il nostro bypass della regione nel secondo modo nella forma della somma di due integrali.

Risposta scrivi così:

Qual è il miglior ordine di bypass? Certo, quello che è stato fornito nelle condizioni del problema: i calcoli saranno la metà!

Esempio 6

Modificare l'ordine di integrazione

Questo è un esempio fai da te. Contiene semicerchi, che sono stati trattati in dettaglio nell'Esempio 3. Una soluzione di esempio alla fine della lezione.

E ora il compito promesso, quando inizialmente è impostato il secondo modo per aggirare l'area:

Esempio 7

Modificare l'ordine di integrazione

Soluzione: Quando l'ordine di bypass è impostato nel secondo modo, è consigliabile passare alle funzioni "normali" prima di disegnare il disegno. In questo esempio, ci sono due pazienti da convertire: e .
Con una funzione lineare, tutto è semplice:

Il grafico della funzione è una parabola con pretesa di canonicità.

Esprimiamo "Y" tramite "X":

Otteniamo due rami della parabola: e . Quale scegliere? Il modo più semplice è eseguire immediatamente il disegno. E anche se hai dimenticato il materiale geometria analitica su una parabola, allora entrambi i rami possono ancora essere costruiti a punti:

Ancora una volta, vorrei attirare la vostra attenzione sul fatto che questo disegno Ho diverse figure piatte ed è molto importante scegliere la forma giusta! Nella scelta della figura desiderata, i limiti di integrazione degli integrali originali aiuteranno solo:
e non dimenticare che la funzione inversa imposta tutto parabola.

Le frecce che indicano il bypass della figura corrispondono esattamente ai limiti di integrazione degli integrali .

Molto presto imparerai a svolgere mentalmente tale analisi e a trovare l'area di integrazione desiderata.

Una volta trovata la forma, la parte finale della soluzione è, in genere, molto semplice, cambiare l'ordine di attraversamento dell'area:

Le funzioni inverse sono già state trovate e l'ordine di attraversamento richiesto della regione è:

Risposta:

Esempio finale di paragrafo per l'autorisoluzione:

Esempio 8

Modificare l'ordine di integrazione

Soluzione completa e la risposta alla fine della lezione.

Iniziamo a considerare il processo effettivo di calcolo dell'integrale doppio e a familiarizzare con il suo significato geometrico.

Il doppio integrale è numericamente uguale all'area di una figura piatta (regione di integrazione). esso la forma più semplice integrale doppio quando la funzione di due variabili è uguale a uno: .

Consideriamo innanzitutto il problema in termini generali. Ora rimarrai sorpreso da quanto sia davvero semplice! Calcoliamo l'area di una figura piatta delimitata da linee. Per certezza, assumiamo che sull'intervallo . L'area di questa figura è numericamente uguale a:

Descriviamo l'area nel disegno:

Scegliamo il primo modo per aggirare l'area:

In questo modo:

E subito un importante accorgimento tecnico: gli integrali iterati possono essere considerati separatamente. Prima l'integrale interno, poi l'integrale esterno. Questo metodo Altamente raccomandato per i principianti nell'argomento teiere.

1) Calcolare l'integrale interno, mentre l'integrazione avviene sulla variabile "y":

Integrale indefinito ecco la più semplice, e poi si usa la banale formula di Newton-Leibniz, con l'unica differenza che i limiti dell'integrazione non sono i numeri, ma le funzioni. In primo luogo, abbiamo sostituito il limite superiore nella "y" (funzione antiderivativa), quindi il limite inferiore

2) Il risultato ottenuto nel primo comma deve essere sostituito nell'integrale esterno:

Una notazione più compatta per l'intera soluzione si presenta così:

La formula risultante - questa è esattamente la formula di lavoro per calcolare l'area di una figura piatta usando l'integrale definito "ordinario"! Vedi lezione Calcolo dell'area utilizzando un integrale definito, eccola a ogni angolo!

Questo è, il problema del calcolo dell'area utilizzando un integrale doppio poco diverso dal problema di trovare l'area usando un integrale definito! In effetti, sono la stessa cosa!

Di conseguenza, non dovrebbero sorgere difficoltà! Non prenderò in considerazione molti esempi, poiché tu, in effetti, hai riscontrato ripetutamente questo problema.

Esempio 9

Usando l'integrale doppio, calcola l'area di una figura piana delimitata da linee.

Soluzione: Descriviamo l'area nel disegno:

L'area della figura viene calcolata utilizzando il doppio integrale secondo la formula:

Scegliamo il seguente ordine di attraversamento della regione:

Qui e sotto, non entrerò in come attraversare un'area perché il primo paragrafo era molto dettagliato.

In questo modo:

Come ho già notato, è meglio per i principianti calcolare gli integrali iterati separatamente, aderirò allo stesso metodo:

1) Innanzitutto, usando la formula di Newton-Leibniz, trattiamo l'integrale interno:

2) Il risultato ottenuto al primo passo è sostituito nell'integrale esterno:

Il punto 2 sta effettivamente trovando l'area di una figura piatta usando un integrale definito.

Risposta:

Ecco un compito così stupido e ingenuo.

Un curioso esempio di soluzione indipendente:

Esempio 10

Usando l'integrale doppio, calcola l'area di una figura piana delimitata dalle linee , ,

Un esempio di soluzione finale alla fine della lezione.

Negli Esempi 9-10, è molto più vantaggioso utilizzare il primo metodo per aggirare l'area; lettori curiosi, tra l'altro, possono modificare l'ordine del bypass e calcolare le aree nel secondo modo. Se non si commette un errore, naturalmente si ottengono gli stessi valori dell'area.

Per una funzione di due variabili, definita come z = f(X, y) .

L'integrale doppio si scrive come segue:

Qui D- forma piatta delimitato da linee, le cui espressioni (uguaglianze) sono date nel compito di calcolare l'integrale doppio. Sinistra e destra - uguaglianze, in cui la variabile a sinistra X, e sopra e sotto - per uguaglianze, in cui la variabile a sinistra y. Questo posto e oltre è uno dei più importanti per comprendere la tecnica di calcolo dell'integrale doppio.

Calcola il doppio integrale - significa trovare un numero uguale all'area della cifra menzionata D .

Fino a quando non ci tocchiamo definizioni dell'integrale doppio , e impareremo a calcolarlo. È più facile capire cos'è un integrale doppio quando sono stati risolti diversi problemi per calcolarlo, quindi troverai la definizione di integrale doppio alla fine di questa lezione. Guardando un po' avanti, possiamo solo notare che la definizione dell'integrale doppio è anche associata alla figura citata D .

Se la figura Dè un rettangolo, tutte le linee che lo delimitano sono rette. Se la figura D- curvilineo, quindi a sinistra ea destra è limitato da linee rette, e dall'alto e dal basso - da linee curve date dalle uguaglianze date nel compito. Ci sono anche casi in cui una figura D- un triangolo, ma su questi casi un po 'più in là.

Per calcolare l'integrale doppio è quindi necessario ordinare le linee che delimitano la figura D, che ha un nome rigoroso: la regione dell'integrazione. Ordina in sinistra e destra e in alto e in basso. Questo sarà richiesto quando riduzione dell'integrale doppio all'integrale iterato – il metodo di calcolo dell'integrale doppio.

Cassa ad area rettangolare:

Caso della regione curvilinea:

E questa è già una soluzione degli integrali definiti a noi familiari, in cui sono posti i limiti superiore e inferiore dell'integrazione. Espressioni che definiscono le linee che delimitano una forma D, saranno i limiti di integrazione per i soliti integrali definiti, a cui ci stiamo già avvicinando.

Riduzione dell'integrale doppio a iterato

Cassa ad area rettangolare

Lascia che una tale funzione abbia un integrale doppio

Per calcola questo doppio integrale , è necessario ridurlo all'integrale iterato, che ha la forma

.

Per prima cosa devi calcolare l'integrale definito interno (destra), quindi l'integrale definito esterno (sinistra).

Puoi cambiare ruolo X e y

.

Esempio 1 Calcola il doppio integrale

Calcoliamo l'integrale interno (destra), considerando y una costante. Noi riceviamo.

.

Esempio 2 Calcola il doppio integrale

,

Soluzione. Riduciamo questo integrale doppio all'integrale iterato

Sul disegno costruiamo l'area di integrazione:

Ora calcoliamo l'integrale esterno (sinistra) dall'integrale interno (destra) appena calcolato:

Il risultato sarà la soluzione di questo integrale doppio.

Calcola tu stesso l'integrale doppio e poi vedi la soluzione

Caso della regione curvilinea o triangolare

Sia data ancora una funzione di due variabili f(X, y) , e le restrizioni per D: ha un aspetto leggermente diverso:

Questa voce significa che la figura D limite a sinistra ea destra, come nel caso di una regione rettilinea - linee rette X = un e X = b, ma sotto e sopra ci sono le curve date dalle equazioni e . In altre parole, e sono funzioni.

Lascia che una tale funzione abbia anche un integrale doppio

Per calcolare questo integrale doppio, dobbiamo ridurlo all'integrale iterato, che ha la forma

.

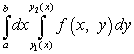Ecco i limiti dell'integrazione un e b sono numeri e e sono funzioni. Nel caso di una regione triangolare, una delle funzioni o è l'equazione di una retta. Questo caso sarà discusso nell'Esempio 3.

Come nel caso di una regione rettilinea, devi prima calcolare l'integrale definito destro, poi l'integrale definito sinistro.

Puoi anche cambiare ruolo allo stesso modo. X e y. Quindi integrale iterato sembrerà

.

Tale integrale iterato deve essere risolto esattamente allo stesso modo: prima l'integrale interno (destra), poi l'integrale esterno (sinistra).

Esempio 5 Calcola il doppio integrale

,

Soluzione. Riduciamo questo integrale doppio all'integrale iterato

.

Sul disegno costruiamo l'area di integrazione e vediamo che è triangolare:

Calcoliamo l'integrale interno (destra), considerando x come una costante. Noi riceviamo.

Ora calcoliamo l'integrale esterno (sinistra) dell'integrale interno (destra) appena calcolato. Innanzitutto, rappresentiamo questo integrale come somma di integrali:

.

Calcoliamo il primo termine:

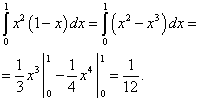
Calcoliamo il secondo termine:

Calcoliamo il terzo termine:

Otteniamo la somma, che sarà la soluzione di questo integrale doppio:

.

Esempio 6 Calcola il doppio integrale

Soluzione. Riduciamo questo integrale doppio all'integrale iterato

Sul disegno costruiamo l'area di integrazione:

Calcoliamo l'integrale interno (destra), considerando x come una costante. Noi riceviamo.

.

Ora calcoliamo l'integrale esterno (sinistra) dall'integrale interno (destra) appena calcolato:

Il risultato sarà la soluzione di questo integrale doppio.

X- giusto e sbagliato y-domini di integrazione corretti e non corretti

Succede che l'area di integrazione di un integrale doppio è limitata da tali linee che diventa necessario dividere l'area di integrazione in parti e risolvere separatamente ciascun integrale iterato corrispondente. Questi sono i casi in cui:

1) l'area di integrazione è una figura che ha due o più due linee rette o curve sotto forma di confine inferiore o superiore (sinistra o destra);

2) l'area di integrazione è una figura il cui confine le linee si intersecano in più di due punti.

Se quanto sopra vale per il confine sinistro o destro della regione di integrazione, cioè i vincoli dati dalle linee espresse attraverso X, allora viene chiamato il dominio di integrazione X- sbagliato. Se una linea retta y = y0 interseca il confine corrispondente solo in un punto e se solo una linea o una curva funge da confine, viene chiamata la regione di integrazione X-corretta

Allo stesso modo, se il confine definito da linee espresse in termini di y, dritto X = X0 si interseca in più di un punto, o se più di una linea o curva funge da confine, allora si chiama l'area di integrazione y- sbagliato. Tira fuori i segni ora y-l'area giusta, presumibilmente, molto semplicemente.

Finora abbiamo considerato esempi di X- errato e y-aree regolari di integrazione. Consideriamo ora i casi in cui viene violata la condizione di correttezza.

Esempio 7 Calcola un integrale doppio la cui area di integrazione è limitata da linee y = X , xy = 1 , y = 2 .

Soluzione. L'area di integrazione è y-non corretto, poiché il suo bordo inferiore non può essere impostato con una sola riga y = y(X) . Come puoi vedere nella figura sopra, il limite inferiore è composto da y = X(marrone scuro) e xy= 1 (verde). Quindi diretto X= 1 (nero) possiamo dividere l'area di integrazione in due parti - e .

Questo integrale doppio è calcolato come segue:

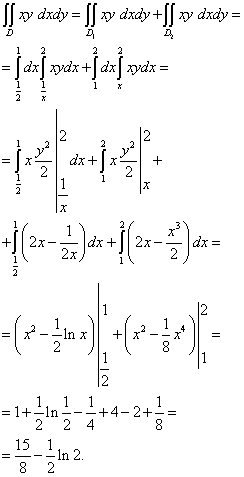
Modifica dell'ordine di integrazione

Come notato sopra, dopo aver ridotto l'integrale doppio all'integrale iterato, è possibile modificare le variabili X e y ruoli o, in altre parole, modificare l'ordine di integrazione.

Il cambiamento nell'ordine di integrazione può essere descritto figurativamente dalle seguenti parole di O "Henry:" Ecco come si comporta l'abitante della giungla: la bestia, entrata nella gabbia, ed è così che si comporta l'abitante della gabbia - un uomo, perso nella giungla dei dubbi. "Il risultato, anche secondo O" Henry, è lo stesso: "Chalmers ha strappato la lettera in mille piccoli pezzi e ha cominciato a tormentare il suo costoso tappeto, facendolo tornare indietro e via." ( O.Henry. Scheherazade da Madison Square.)

Quindi, se abbiamo l'integrale sinistro sulla variabile X, e quello giusto y, quindi dopo aver modificato l'ordine di integrazione, tutto sarà viceversa. Quindi i limiti di integrazione per la "nuova" y devono essere "presi in prestito" dalla "vecchia" x, e i limiti di integrazione per la "nuova" x devono essere ottenuti nella forma funzione inversa, risolvendo l'equazione rispetto a x che fissava il limite per y.

Esempio 8

.

Soluzione. Dopo aver cambiato l'ordine di integrazione, l'integrale su y diventa sinistro e l'integrale su x diventa destro. Prenderemo in prestito i limiti di integrazione per il "nuovo" giocatore dalla "vecchia" X, ovvero il limite inferiore è uguale a zero e il limite superiore è uguale a uno. I limiti di integrazione per il "vecchio" player sono dati dalle equazioni e . Dopo aver risolto queste equazioni rispetto a x, otteniamo nuovi limiti di integrazione per x:

(inferiore) e (superiore).

Pertanto, dopo aver modificato l'ordine di integrazione, l'integrale iterato verrà scritto come segue:

.

Dopo aver cambiato l'ordine di integrazione nel doppio integrale, il dominio di integrazione diventa spesso y- sbagliato o X- errato (vedi paragrafo precedente). Quindi è necessario dividere la regione di integrazione in parti e risolvere separatamente ciascun integrale iterato corrispondente.

Poiché la divisione del dominio di integrazione in parti presenta alcune difficoltà per molti studenti, non ci limiteremo all'esempio dato nel paragrafo precedente, ma analizzeremo un altro paio di esempi.

Esempio 9 Modificare l'ordine di integrazione per l'integrale iterato

.

Soluzione. Quindi, l'area di integrazione di questo integrale iterato è limitata dalle rette y = 1 , y = 3 , X = 0 , X = 2y .

Quando si integra in un ordine diverso, il limite inferiore della regione è costituito da due rette: AB e AVANTI CRISTO, che sono dati dalle equazioni y= 1 e y = X/2 , che può essere visto nella figura seguente.

La via d'uscita da tale incertezza è dividere il dominio di integrazione in due parti. L'area di integrazione sarà divisa da una linea retta BM. I nuovi limiti di integrazione sono calcolati trovando funzione inversa. Secondo questa soluzione, l'integrale iterato dopo aver cambiato l'ordine di integrazione sarà uguale alla somma di due integrali:

Naturalmente la soluzione dell'integrale doppio sarà la stessa, che si riduce all'integrale iterato dato nella condizione di questo esempio.

Esempio 10 Modificare l'ordine di integrazione per l'integrale iterato

.

Soluzione. Quindi, l'area di integrazione dell'integrale iterato è limitata dalle rette X = 0 , X= 2 e curve e .

Come si può vedere nella figura sottostante, una retta parallela all'asse 0x, intersecherà il limite inferiore della regione di integrazione in più di due punti.

Pertanto, dividiamo il dominio di integrazione in tre parti da linee rette, che sono disegnate in nero nella figura. I nuovi limiti di integrazione vengono calcolati trovando la funzione inversa. I limiti per le tre nuove aree di integrazione saranno i seguenti.

Secondo questa soluzione, l'integrale ripetuto dopo aver cambiato l'ordine di integrazione sarà uguale alla somma di tre integrali:

La stessa somma di tre integrali sarà uguale all'integrale doppio, che si riduce all'integrale iterato dato nella condizione di questo esempio.

Eppure, le circostanze di forza maggiore spesso interferiscono con gli studenti già nella fase precedente, stabilendo i limiti dell'integrazione. L'ansia e la confusione non sono prive di basi: se di solito è sufficiente guardare il disegno per dividere il dominio di integrazione in parti e per risolvere l'integrale iterato - la tabella degli integrali, allora è necessaria una certa esperienza di formazione per stabilire i limiti di integrazione. Facciamo un esempio in cui ci soffermiamo solo sulla disposizione dei limiti dell'integrazione e - quasi automaticamente - sulla divisione del territorio e tralasciamo la soluzione stessa.

Esempio 11. Trova i limiti di integrazione di un integrale doppio se l'area di integrazione D impostare come segue:

y - 2X ≤ 0;
2 anni - X ≥ 0;
xy ≤ 2.

Soluzione. esplicitamente (tramite X e y"senza impurità") non sono specificate le linee che limitano l'area di integrazione. Poiché per x si rivelano molto spesso rette che toccano in un punto i limiti superiore e inferiore espressi attraverso y, allora andremo esattamente lungo questo percorso. Inoltre, cambiando l'ordine di integrazione, otteniamo un'area di integrazione con la stessa area. Risolviamo le disuguaglianze per il giocatore e otteniamo:

y ≤ 2X;
y ≥ X/2;
y ≤ 2/X.

Costruiamo le linee risultanti sul disegno. I limiti di integrazione rispetto a x sono infatti le rette X= 0 e X= 2. Ma la regione dell'integrazione si è rivelata essere y-non corretto, poiché il suo bordo superiore non può essere impostato con una riga y = y(X) .

1.1 Definizione dell'integrale doppio

1.2 Proprietà dell'integrale doppio

Le proprietà dell'integrale doppio (e la loro derivazione) sono simili alle corrispondenti proprietà dell'integrale unico definito.

1°. Additività. Se la funzione f(x, y) è integrabile nel dominio D e se il dominio D è diviso da una curva à di area zero in due domini connessi D 1 e D 2 senza punti interni comuni, allora la funzione f(x, y) è integrabile in ciascuna dalle regioni D 1 e D 2 , e

2°. Proprietà lineare. Se le funzioni f(x, y) e g(x, y) sono integrabili nel dominio D, eh? e? - qualunque numeri reali, quindi la funzione [? f(x, y) + ? g(x, y)] è anche integrabile nel dominio D, e

3°. Se le funzioni f(x, y) e g(x, y) sono integrabili nel dominio D, allora il prodotto di queste funzioni è integrabile anche in D.

4°. Se le funzioni f(x, y) e g(x, y) sono entrambe integrabili nel dominio D e ovunque in questo dominio f(x, y) ? g(x, y), allora

5°. Se la funzione f(x, y) è integrabile nel dominio D, allora la funzione |f(x, y)| è integrabile nel dominio D, e

(Naturalmente, l'integrabilità di |f(x, y)| in D non implica l'integrabilità di f(x, y) in D.)

6°. Il teorema del valore medio. Se entrambe le funzioni f(x, y) e g(x, y) sono integrabili in un dominio D, la funzione g(x, y) è non negativa (non positiva) ovunque in questo dominio, M e m sono le migliori limiti superiore e inferiore della funzione f( x, y) nel dominio D, allora esiste un numero che soddisfa la disuguaglianza m ? ? ? M e tale che la formula

In particolare, se la funzione f(x, y) è continua in D, e il dominio D è connesso, allora in questo dominio c'è un tale punto (?, ?), cosa? = f(?, ?), e la formula diventa

7°. Importante proprietà geometrica. pari all'area della regione D

Sia dato un corpo T nello spazio (Fig. 2.1), delimitato dal basso dalla regione D, dall'alto - dal grafico di una funzione continua e non negativa) z \u003d f (x, y,) che è definito nella regione D, dai lati - da una superficie cilindrica, la cui guida è il dominio di confine D, ei generatori sono paralleli all'asse di Oz. Un corpo di questo tipo è chiamato corpo cilindrico.

1.3 Interpretazione geometrica dell'integrale doppio

1.4 Il concetto di integrale doppio per un rettangolo

Sia definita una funzione arbitraria f(x, y) ovunque sul rettangolo R = ? (Vedi Fig. 1).

Dividiamo il segmento a ? X? b in n segmenti parziali usando i punti a = x 0< x 1 < x 2 < ... < x n = b, а сегмент c ? y ? d на p частичных сегментов при помощи точек c = y 0 < y 1 < y 2 < ... < y p = d.

Questa divisione con l'aiuto di linee, parallelamente agli assi Ox e Oy, corrisponde alla divisione del rettangolo R in n · p rettangoli parziali R kl = ? (k = 1, 2, ..., n; l = 1, 2, ..., p). La partizione specificata del rettangolo R sarà indicata dal simbolo T. Nel seguito, in questa sezione, il termine "rettangolo" indicherà un rettangolo con i lati paralleli agli assi delle coordinate.

Su ogni rettangolo parziale R kl, scegliamo un punto arbitrario (? k , ? l). Mettendo?x k = x k - x k-1 , ?y l = y l - y l-1 , indichiamo con ?R kl l'area del rettangolo R kl . Ovviamente, ?R kl = ?x k ?y l .

è detta somma integrale della funzione f(x, y) corrispondente ad una data partizione T del rettangolo R ed una data scelta di punti intermedi (?k, ?l) sui rettangoli parziali della partizione T.

La diagonale sarà chiamata diametro del rettangolo R kl . Un simbolo? denotare il più grande dei diametri di tutti i rettangoli parziali R kl .

Il numero I è detto limite delle somme intere (1) per? > 0 se per qualsiasi numero positivo? puoi specificarlo numero positivo?, cosa a?< ? независимо от выбора точек (? k , ? l) на частичных прямоугольниках R выполняется равенство

| ? - Io |< ?.

Una funzione f(x, y) si dice integrabile (secondo Riemann) su un rettangolo R se esiste un limite finito I delle somme intere di questa funzione a? > 0.

Questo limite I è chiamato integrale doppio della funzione f(x, y) sul rettangolo R ed è indicato da uno dei seguenti simboli:

Commento. Allo stesso modo dell'integrale definito un tempo, si stabilisce che qualsiasi funzione f(x, y) integrabile sul rettangolo R è limitata su questo rettangolo.

Questo dà motivo di considerare solo in quanto segue funzionalità limitate f(x, y).