La somma dei numeri in una formula di progressione geometrica. Progressione geometrica nei compiti dell'esame di matematica

Consideriamo una serie.

7 28 112 448 1792...

È assolutamente chiaro che il valore di uno qualsiasi dei suoi elementi è esattamente quattro volte maggiore del precedente. Quindi questa serie è una progressione.

Una progressione geometrica è una sequenza infinita di numeri, la cui caratteristica principale è che il numero successivo si ottiene dal precedente moltiplicandolo per un numero specifico. Ciò è espresso dalla seguente formula.

a z +1 =a z q, dove z è il numero dell'elemento selezionato.

Di conseguenza, z ∈ N.

Il periodo in cui si studia una progressione geometrica a scuola è il grado 9. Gli esempi ti aiuteranno a capire il concetto:

0.25 0.125 0.0625...

Sulla base di questa formula, il denominatore della progressione può essere trovato come segue:

Né q né b z possono essere zero. Inoltre, ciascuno degli elementi della progressione non dovrebbe essere uguale a zero.

Di conseguenza, per scoprire il numero successivo della serie, devi moltiplicare l'ultimo per q.

Per specificare questa progressione, è necessario specificare il suo primo elemento e denominatore. Successivamente, è possibile trovare uno qualsiasi dei termini successivi e la loro somma.

Varietà

A seconda di q e a 1, questa progressione è suddivisa in diversi tipi:

Se sia a 1 che q sono maggiori di uno, allora tale sequenza è una progressione geometrica crescente con ogni elemento successivo. Un esempio di tale è presentato di seguito.

Esempio: a 1 =3, q=2 - entrambi i parametri sono maggiori di uno.

Quindi sequenza numerica si può scrivere così:

3 6 12 24 48 ...

Se |q| minore di uno, cioè moltiplicare per esso equivale a divisione, quindi una progressione con condizioni simili è una progressione geometrica decrescente. Un esempio di tale è presentato di seguito.

Esempio: a 1 =6, q=1/3 - a 1 è maggiore di uno, q è minore.

Quindi la sequenza numerica può essere scritta come segue:

6 2 2/3 ... - qualsiasi elemento è 3 volte maggiore dell'elemento che lo segue.

Segno-variabile. Se q<0, то знаки у чисел последовательности постоянно чередуются вне зависимости от a 1 , а элементы ни возрастают, ни убывают.

Esempio: a 1 = -3 , q = -2 - entrambi i parametri sono minori di zero.

Quindi la sequenza può essere scritta in questo modo:

3, 6, -12, 24,...

Formule

Per un comodo utilizzo delle progressioni geometriche, ci sono molte formule:

Formula del membro z-esimo. Consente di calcolare l'elemento sotto un numero specifico senza calcolare i numeri precedenti.

Esempio:Q = 3, un 1 = 4. Occorre calcolare il quarto elemento della progressione.

Soluzione:un 4 = 4 · 3 4-1 = 4 · 3 3 = 4 · 27 = 108.

La somma dei primi elementi il cui numero è z. Consente di calcolare la somma di tutti gli elementi di una sequenza fino aazcompreso.

Dal (1-Q) è al denominatore, quindi (1 - q)≠ 0, quindi q non è uguale a 1.

Nota: se q=1, la progressione sarebbe una serie di numeri che si ripetono all'infinito.

Somma progressione geometrica, esempi:un 1 = 2, Q= -2. Calcola S 5 .

Soluzione:S 5 = 22 - calcolo per formula.

Importo se |Q| < 1 и если z стремится к бесконечности.

Esempio:un 1 = 2 , Q= 0,5. Trova l'importo.

Soluzione:Sz = 2 · = 4

Sz = 2 + 1 + 0.5 + 0.25 + 0.125 + 0.0625 = 3.9375 4

Alcune proprietà:

proprietà caratteristica. Se la seguente condizione eseguita per qualsiasiz, allora la serie numerica data è una progressione geometrica:

az 2 = az -1 · unz+1

Inoltre, il quadrato di qualsiasi numero di una progressione geometrica si trova sommando i quadrati di altri due numeri qualsiasi in una data serie, se equidistanti da questo elemento.

az 2 = az - T 2 + az + T 2 , doveTè la distanza tra questi numeri.

Elementidifferiscono in quna volta.
Anche i logaritmi degli elementi di progressione formano una progressione, ma già aritmetica, cioè ciascuno di essi è maggiore del precedente di un certo numero.

Esempi di alcuni problemi classici

Per capire meglio cos'è una progressione geometrica, possono essere utili esempi con una soluzione per il grado 9.

Termini:un 1 = 3, un 3 = 48. TrovaQ.

Soluzione: ogni elemento successivo è maggiore del precedente inQ una volta.È necessario esprimere alcuni elementi attraverso altri utilizzando un denominatore.

Di conseguenza,un 3 = Q 2 · un 1

Quando si sostituisceQ= 4

Termini:un 2 = 6, un 3 = 12. Calcola S 6 .

Soluzione:Per fare ciò, è sufficiente trovare q, il primo elemento e sostituirlo nella formula.

un 3 = Q· un 2 , Di conseguenza,Q= 2

a 2 = q un 1,Ecco perché un 1 = 3

S 6 = 189

· un 1 = 10, Q= -2. Trova il quarto elemento della progressione.

Soluzione: per fare ciò è sufficiente esprimere il quarto elemento attraverso il primo e attraverso il denominatore.

a 4 = q 3· a 1 = -80

Esempio di applicazione:

Il cliente della banca ha effettuato un deposito per un importo di 10.000 rubli, in base ai quali ogni anno il cliente aggiungerà il 6% all'importo principale. Quanti soldi ci saranno sul conto dopo 4 anni?

Soluzione: l'importo iniziale è di 10 mila rubli. Quindi, un anno dopo l'investimento, il conto avrà un importo pari a 10.000 + 10.000 · 0,06 = 10000 1,06

Di conseguenza, l'importo nel conto dopo un altro anno sarà espresso come segue:

(10000 1,06) 0,06 + 10000 1,06 = 1,06 1,06 10000

Cioè, ogni anno l'importo aumenta di 1,06 volte. Ciò significa che per trovare l'importo dei fondi sul conto dopo 4 anni, è sufficiente trovare il quarto elemento della progressione, che è dato dal primo elemento pari a 10mila, e il denominatore pari a 1,06.

S = 1,06 1,06 1,06 1,06 10000 = 12625

Esempi di attività per il calcolo della somma:

In vari problemi viene utilizzata una progressione geometrica. Un esempio per trovare la somma può essere dato come segue:

un 1 = 4, Q= 2, calcolaS5.

Soluzione: tutti i dati necessari per il calcolo sono noti, basta sostituirli nella formula.

S 5 = 124

un 2 = 6, un 3 = 18. Calcola la somma dei primi sei elementi.

Soluzione:

Geom. progressione, ogni elemento successivo è q volte maggiore del precedente, cioè per calcolare la somma è necessario conoscere l'elementoun 1 e denominatoreQ.

un 2 · Q = un 3

Q = 3

Allo stesso modo, dobbiamo trovareun 1 , sapendoun 2 eQ.

un 1 · Q = un 2

un 1 =2

S 6 = 728.

Quindi sediamoci e iniziamo a scrivere dei numeri. Per esempio:

Puoi scrivere qualsiasi numero e ce ne possono essere quanti ne vuoi (nel nostro caso, loro). Non importa quanti numeri scriviamo, possiamo sempre dire quale di essi è il primo, quale è il secondo e così via fino all'ultimo, cioè possiamo numerarli. Questo è un esempio di sequenza numerica:

Sequenza numericaè un insieme di numeri, a ciascuno dei quali può essere assegnato un numero univoco.

Ad esempio, per la nostra sequenza:

Il numero assegnato è specifico per un solo numero di sequenza. In altre parole, non ci sono numeri di tre secondi nella sequenza. Il secondo numero (come il -esimo numero) è sempre lo stesso.

Il numero con il numero è chiamato -esimo membro della sequenza.

Di solito chiamiamo l'intera sequenza una lettera (ad esempio) e ogni membro di questa sequenza - la stessa lettera con un indice uguale al numero di questo membro: .

Nel nostro caso:

I tipi più comuni di progressione sono aritmetica e geometrica. In questo argomento, parleremo del secondo tipo - progressione geometrica.

Perché abbiamo bisogno di una progressione geometrica e della sua storia.

Già nell'antichità il matematico italiano, il monaco Leonardo da Pisa (meglio noto come Fibonacci), si occupava delle esigenze pratiche del commercio. Il monaco si trovava di fronte al compito di determinare qual è il minor numero di pesi che può essere utilizzato per pesare la merce? Fibonacci nei suoi scritti dimostra che un tale sistema di pesi è ottimale: questa è una delle prime situazioni in cui le persone hanno dovuto fare i conti con una progressione geometrica, di cui probabilmente hai sentito parlare e di cui hai almeno un'idea generale. Una volta compreso appieno l'argomento, pensa al motivo per cui un tale sistema è ottimale?

Attualmente, nella pratica della vita, si manifesta una progressione geometrica quando si investe denaro in una banca, quando l'importo degli interessi viene addebitato sull'importo accumulato sul conto per il periodo precedente. In altre parole, se metti denaro su un deposito a termine in una cassa di risparmio, in un anno il deposito aumenterà dall'importo originale, cioè il nuovo importo sarà pari al contributo moltiplicato per. In un altro anno, questo importo aumenterà di, i.е. l'importo ottenuto in quel momento viene nuovamente moltiplicato per e così via. Una situazione simile è descritta nei problemi di calcolo del cosiddetto interesse composto- la percentuale viene prelevata di volta in volta dall'importo che è sul conto, tenendo conto degli interessi precedenti. Parleremo di questi compiti un po' più tardi.

Ci sono molti casi più semplici in cui viene applicata una progressione geometrica. Ad esempio, la diffusione dell'influenza: una persona ha infettato una persona, a sua volta ha infettato un'altra persona, e quindi la seconda ondata di infezione è una persona e, a sua volta, ne ha infettata un'altra ... e così via .. .

A proposito, la piramide finanziaria, la stessa MMM, è un calcolo semplice e asciutto secondo le proprietà di una progressione geometrica. Interessante? Scopriamolo.

Progressione geometrica.

Diciamo di avere una sequenza numerica:

Risponderai immediatamente che è facile e il nome di una tale sequenza è a differenza dei suoi membri. Che ne dici di qualcosa del genere:

Se sottrai il numero precedente dal numero successivo, vedrai che ogni volta ottieni una nuova differenza (e così via), ma la sequenza esiste sicuramente ed è facile da notare: ogni numero successivo è volte più grande del precedente !

Questo tipo di sequenza viene chiamato progressione geometrica ed è segnato.

Una progressione geometrica ( ) è una sequenza numerica, il cui primo termine è diverso da zero, e ogni termine, a partire dal secondo, è uguale al precedente, moltiplicato per lo stesso numero. Questo numero è chiamato denominatore di una progressione geometrica.

I vincoli che il primo termine ( ) non è uguale e non sono casuali. Diciamo che non ce ne sono, e il primo termine è ancora uguale, e q è, hmm .. lascia, quindi risulta:

Concordo sul fatto che questa non è una progressione.

Come capisci, otterremo gli stessi risultati se è un numero diverso da zero, ma. In questi casi, semplicemente non ci sarà alcuna progressione, poiché l'intera serie di numeri sarà composta da tutti zeri o un numero e tutti gli zeri rimanenti.

Parliamo ora più in dettaglio del denominatore di una progressione geometrica, cioè di.

Ancora una volta, questo è il numero quante volte cambia ogni termine successivo progressione geometrica.

Cosa pensi potrebbe essere? Esatto, positivo e negativo, ma non zero (ne abbiamo parlato un po' più in alto).

Diciamo che abbiamo un positivo. Sia nel nostro caso, a. Qual è il secondo termine e? Puoi facilmente rispondere che:

Va bene. Di conseguenza, se tutti i membri successivi della progressione hanno lo stesso segno, loro positivo.

E se fosse negativo? Ad esempio, a. Qual è il secondo termine e?

È una storia completamente diversa

Prova a contare il termine di questa progressione. Quanto hai preso? Io ho. Quindi, se, allora si alternano i segni dei termini della progressione geometrica. Cioè, se vedi una progressione con segni alternati nei suoi membri, il suo denominatore è negativo. Questa conoscenza può aiutarti a metterti alla prova quando risolvi problemi su questo argomento.

Ora facciamo un po' di pratica: proviamo a determinare quali sequenze numeriche sono una progressione geometrica e quali sono una aritmetica:

Fatto? Confronta le nostre risposte:

Progressione geometrica - 3, 6.
Progressione aritmetica - 2, 4.
Non è né una progressione aritmetica né geometrica - 1, 5, 7.

Torniamo alla nostra ultima progressione, e proviamo a trovarne il termine allo stesso modo dell'aritmetica. Come avrai intuito, ci sono due modi per trovarlo.

Moltiplichiamo successivamente ogni termine per.

Quindi, il -esimo membro della progressione geometrica descritta è uguale a.

Come già intuisci, ora tu stesso ricaverai una formula che ti aiuterà a trovare qualsiasi membro di una progressione geometrica. O l'hai già tirato fuori di persona, descrivendo come trovare il esimo membro in più fasi? In tal caso, verifica la correttezza del tuo ragionamento.

Illustriamo questo con l'esempio di trovare il -esimo membro di questa progressione:

In altre parole:

Trova il valore di un membro di una data progressione geometrica.

È accaduto? Confronta le nostre risposte:

Fai attenzione che hai ottenuto esattamente lo stesso numero del metodo precedente, quando abbiamo moltiplicato successivamente per ogni membro precedente della progressione geometrica.
Proviamo a "spersonalizzare" questa formula: la portiamo in una forma generale e otteniamo:

La formula derivata è vera per tutti i valori, sia positivi che negativi. Verificalo tu stesso calcolando i termini di una progressione geometrica con le seguenti condizioni: , a.

Hai contato? Confrontiamo i risultati:

D'accordo sul fatto che sarebbe possibile trovare un membro della progressione allo stesso modo di un membro, tuttavia, esiste la possibilità di errori di calcolo. E se abbiamo già trovato il esimo termine di una progressione geometrica, a, allora cosa potrebbe essere più facile che usare la parte “troncata” della formula.

Una progressione geometrica infinitamente decrescente.

Più recentemente abbiamo parlato di cosa può essere maggiore o minore di zero, tuttavia ci sono valori speciali per i quali si chiama progressione geometrica infinitamente decrescente.

Perché pensi che abbia un nome così?
Per cominciare, scriviamo una progressione geometrica composta da membri.
Diciamo, allora:

Vediamo che ogni termine successivo è minore del precedente in tempi, ma ci sarà un numero? Risponderai subito "no". Ecco perché l'infinitamente decrescente - diminuisce, diminuisce, ma non diventa mai zero.

Per capire chiaramente come appare visivamente, proviamo a tracciare un grafico della nostra progressione. Quindi, nel nostro caso, la formula assume la seguente forma:

Sui grafici siamo abituati a costruire dipendenza, quindi:

L'essenza dell'espressione non è cambiata: nella prima voce, abbiamo mostrato la dipendenza del valore di un membro di progressione geometrica dal suo numero ordinale, e nella seconda voce, abbiamo semplicemente preso il valore di un membro di progressione geometrica per, e il numero ordinale è stato designato non come, ma come. Tutto ciò che resta da fare è tracciare il grafico.
Vediamo cosa hai. Ecco lo schema che ho ottenuto:

Vedere? La funzione decresce, tende a zero, ma non la attraversa mai, quindi è infinitamente decrescente. Segnaliamo i nostri punti sul grafico e allo stesso tempo quali coordinate e significa:

Prova a rappresentare schematicamente un grafico di una progressione geometrica se anche il suo primo termine è uguale. Analizza qual è la differenza con il nostro grafico precedente?

Sei riuscito? Ecco lo schema che ho ottenuto:

Ora che hai compreso appieno le basi dell'argomento progressione geometrica: sai di cosa si tratta, sai come trovarne il termine, e sai anche cos'è una progressione geometrica infinitamente decrescente, passiamo alla sua proprietà principale.

proprietà di una progressione geometrica.

Ricordi la proprietà dei membri di una progressione aritmetica? Sì, sì, come trovare il valore di un certo numero di una progressione quando ci sono valori precedenti e successivi dei membri di questa progressione. Ricordato? Questo:

Ora ci troviamo di fronte esattamente alla stessa domanda per i termini di una progressione geometrica. Per derivare una tale formula, iniziamo a disegnare e ragionare. Vedrai, è molto facile e, se dimentichi, puoi tirarlo fuori tu stesso.

Prendiamo un'altra semplice progressione geometrica, in cui sappiamo e. Come trovare? Con una progressione aritmetica, questo è facile e semplice, ma come è qui? In effetti, non c'è nulla di complicato nemmeno nella geometria: devi solo dipingere ogni valore che ci viene fornito secondo la formula.

Chiedi, e ora cosa ne facciamo? Sì, molto semplice. Per cominciare, descriviamo queste formule nella figura e proviamo a fare varie manipolazioni con esse per arrivare a un valore.

Astraiamo dai numeri che ci vengono dati, ci concentreremo solo sulla loro espressione attraverso una formula. Dobbiamo trovare il valore evidenziato in arancione, conoscendo i termini ad esso adiacenti. Proviamo a eseguire varie azioni con loro, a seguito delle quali possiamo ottenere.

Aggiunta.
Proviamo ad aggiungere due espressioni e otteniamo:

Da questa espressione, come puoi vedere, non saremo in grado di esprimere in alcun modo, quindi proveremo un'altra opzione: la sottrazione.

Sottrazione.

Come puoi vedere, non possiamo esprimere nemmeno da questo, quindi cercheremo di moltiplicare queste espressioni l'una per l'altra.

Moltiplicazione.

Ora osserviamo con attenzione ciò che abbiamo, moltiplicando i termini di una progressione geometrica che ci è stata data rispetto a ciò che deve essere trovato:

Indovina di cosa sto parlando? Correttamente, per trovarlo, dobbiamo prendere la radice quadrata dei numeri di progressione geometrica adiacenti al numero desiderato moltiplicati tra loro:

Ecco qui. Tu stesso hai dedotto la proprietà di una progressione geometrica. Prova a scrivere questa formula in forma generale. È accaduto?

Hai dimenticato la condizione quando? Pensa al motivo per cui è importante, ad esempio, prova a calcolarlo da solo, a. Cosa succede in questo caso? Esatto, completa sciocchezza, poiché la formula è simile a questa:

Di conseguenza, non dimenticare questa limitazione.

Ora calcoliamo cos'è

Risposta corretta - ! Se non hai dimenticato il secondo valore possibile durante il calcolo, allora sei un bravo ragazzo e puoi immediatamente procedere all'allenamento e, se lo hai dimenticato, leggi ciò che viene analizzato di seguito e presta attenzione al motivo per cui entrambe le radici devono essere scritte nella risposta .

Disegniamo entrambe le nostre progressioni geometriche, una con un valore e l'altra con un valore, e controlliamo se entrambe hanno il diritto di esistere:

Per verificare se una tale progressione geometrica esiste o meno, è necessario vedere se è la stessa tra tutti i suoi membri dati? Calcola q per il primo e il secondo caso.

Vedi perché dobbiamo scrivere due risposte? Perché il segno del termine richiesto dipende se è positivo o negativo! E poiché non sappiamo cosa sia, dobbiamo scrivere entrambe le risposte con un più e un meno.

Ora che hai imparato i punti principali e dedotto la formula per la proprietà di una progressione geometrica, trova, conosce e

Confronta le tue risposte con quelle corrette:

Cosa ne pensi, e se ci venissero forniti non i valori dei membri della progressione geometrica adiacenti al numero desiderato, ma equidistanti da esso. Ad esempio, abbiamo bisogno di trovare, e dare e. Possiamo usare la formula che abbiamo derivato in questo caso? Cerca di confermare o confutare questa possibilità allo stesso modo, descrivendo in cosa consiste ciascun valore, come hai fatto inizialmente derivando la formula.
Cosa hai preso?

Ora guarda di nuovo attentamente.
e corrispondentemente:

Da ciò possiamo concludere che la formula funziona non solo con i vicini con i termini desiderati di una progressione geometrica, ma anche con equidistante da ciò che i membri stanno cercando.

Pertanto, la nostra formula originale diventa:

Cioè, se nel primo caso abbiamo detto questo, ora diciamo che può essere uguale a qualsiasi numero naturale minore. La cosa principale è essere lo stesso per entrambi i numeri dati.

Esercitati su esempi specifici, fai solo molta attenzione!

, . Trovare.
, . Trovare.
, . Trovare.

Deciso? Spero che tu sia stato estremamente attento e abbia notato un piccolo problema.

Confrontiamo i risultati.

Nei primi due casi, applichiamo con calma la formula sopra e otteniamo i seguenti valori:

Nel terzo caso, dopo un'attenta considerazione dei numeri seriali dei numeri che ci vengono forniti, comprendiamo che non sono equidistanti dal numero che stiamo cercando: è il numero precedente, ma rimosso in posizione, quindi non è possibile per applicare la formula.

Come risolverlo? In realtà non è così difficile come sembra! Scriviamo con te in cosa consiste ogni numero che ci è stato dato e il numero desiderato.

Quindi abbiamo e. Vediamo cosa possiamo fare con loro. Suggerisco di dividere. Noi abbiamo:

Sostituiamo i nostri dati nella formula:

Il prossimo passo che possiamo trovare: per questo dobbiamo prendere la radice cubica del numero risultante.

Ora guardiamo di nuovo a quello che abbiamo. Abbiamo, ma dobbiamo trovare, e, a sua volta, è uguale a:

Abbiamo trovato tutti i dati necessari per il calcolo. Sostituisci nella formula:

La nostra risposta: .

Prova a risolvere tu stesso un altro stesso problema:
Dato: ,
Trovare:

Quanto hai preso? Io ho - .

Come puoi vedere, infatti, hai bisogno ricorda una sola formula- . Tutto il resto puoi ritirarlo tu stesso senza alcuna difficoltà in qualsiasi momento. Per fare ciò, scrivi semplicemente la progressione geometrica più semplice su un pezzo di carta e scrivi a cosa è uguale, secondo la formula sopra, ciascuno dei suoi numeri.

La somma dei termini di una progressione geometrica.

Consideriamo ora le formule che ci permettono di calcolare velocemente la somma dei termini di una progressione geometrica in un dato intervallo:

Per derivare la formula per la somma dei termini di una progressione geometrica finita, moltiplichiamo tutte le parti dell'equazione precedente per. Noi abbiamo:

Guarda bene: cosa hanno in comune le ultime due formule? Esatto, membri comuni, ad esempio e così via, ad eccezione del primo e dell'ultimo membro. Proviamo a sottrarre la 1a equazione dalla 2a equazione. Cosa hai preso?

Ora esprimi attraverso la formula di un membro di una progressione geometrica e sostituisci l'espressione risultante nella nostra ultima formula:

Raggruppa l'espressione. Dovresti ricevere:

Non resta che esprimere:

Di conseguenza, in questo caso.

Cosa succede se? Quale formula funziona allora? Immagina una progressione geometrica a. Com'è lei? Correttamente una serie di numeri identici, rispettivamente, la formula sarà simile a questa:

Come per la progressione aritmetica e geometrica, ci sono molte leggende. Uno di questi è la leggenda di Seth, il creatore degli scacchi.

Molte persone sanno che il gioco degli scacchi è stato inventato in India. Quando il re indù l'ha incontrata, è stato deliziato dal suo spirito e dalla varietà di posizioni possibili in lei. Dopo aver appreso che era stato inventato da uno dei suoi sudditi, il re decise di premiarlo personalmente. Chiamò a sé l'inventore e ordinò di chiedergli quello che voleva, promettendo di esaudire anche il desiderio più abile.

Seta chiese tempo per pensare e quando il giorno successivo Seta apparve davanti al re, sorprese il re con l'impareggiabile modestia della sua richiesta. Chiese un chicco di grano per il primo quadrato della scacchiera, grano per il secondo, per il terzo, per il quarto e così via.

Il re si adirò e scacciò Set, dicendo che la richiesta del servo non era degna della generosità regale, ma promise che il servo avrebbe ricevuto i suoi cereali per tutte le celle della tavola.

E ora la domanda è: usando la formula per la somma dei membri di una progressione geometrica, calcola quanti grani dovrebbe ricevere Seth?

Iniziamo a discutere. Poiché, a seconda della condizione, Seth ha chiesto un chicco di grano per la prima cella della scacchiera, per la seconda, per la terza, per la quarta, ecc., vediamo che il problema riguarda una progressione geometrica. Cosa è uguale in questo caso?
Destra.

Celle totali della scacchiera. Rispettivamente, . Abbiamo tutti i dati, resta solo da sostituire nella formula e calcolare.

Per rappresentare almeno approssimativamente le "scale" di un dato numero, trasformiamo usando le proprietà del grado:

Certo, se vuoi, puoi prendere una calcolatrice e calcolare che tipo di numero ti ritroverai, e in caso contrario dovrai credermi sulla parola: il valore finale dell'espressione sarà.
Cioè:

quintilioni quadrilioni trilioni miliardi milioni di migliaia.

Fuh) Se vuoi immaginare l'enormità di questo numero, allora stima quale dimensione sarebbe necessaria per ospitare l'intera quantità di grano.
Con un'altezza del fienile di me una larghezza di m, la sua lunghezza dovrebbe estendersi fino a km, cioè due volte più lontano dalla Terra al Sole.

Se il re fosse forte in matematica, potrebbe offrire allo scienziato stesso il conteggio dei grani, perché per contare un milione di grani avrebbe bisogno almeno di un giorno di instancabile conteggio, e dato che bisogna contare i quintilioni, i grani avrebbero dovuto essere contati per tutta la vita.

E ora risolveremo un semplice problema sulla somma dei termini di una progressione geometrica.
Vasya, una studentessa di quinta elementare, si è ammalata di influenza, ma continua ad andare a scuola. Ogni giorno Vasya infetta due persone che, a loro volta, infettano altre due persone e così via. Solo una persona nella classe. In quanti giorni tutta la classe avrà l'influenza?

Quindi, il primo membro di una progressione geometrica è Vasya, cioè una persona. esimo membro della progressione geometrica, queste sono le due persone che ha contagiato il primo giorno del suo arrivo. La somma totale dei componenti la progressione è pari al numero degli studenti 5A. Di conseguenza, stiamo parlando di una progressione in cui:

Sostituiamo i nostri dati nella formula per la somma dei termini di una progressione geometrica:

L'intera classe si ammalerà in pochi giorni. Non credi nelle formule e nei numeri? Cerca di ritrarre tu stesso l'"infezione" degli studenti. È accaduto? Guarda come mi sembra:

Calcola tu stesso quanti giorni gli studenti prenderebbero l'influenza se tutti contagiassero una persona e ci fosse una persona nella classe.

Che valore hai ottenuto? Si è scoperto che tutti hanno iniziato ad ammalarsi dopo un giorno.

Come puoi vedere, un tale compito e il relativo disegno ricordano una piramide, in cui ogni successivo "porta" nuove persone. Tuttavia, prima o poi arriva un momento in cui quest'ultimo non può attrarre nessuno. Nel nostro caso, se immaginiamo che la classe sia isolata, la persona da cui chiude la catena (). Pertanto, se una persona fosse coinvolta in una piramide finanziaria in cui è stato dato del denaro se hai portato altri due partecipanti, la persona (o nel caso generale) non porterebbe nessuno, rispettivamente, perderebbe tutto ciò che ha investito in questa truffa finanziaria .

Tutto ciò che è stato detto sopra si riferisce a una progressione geometrica decrescente o crescente, ma, come ricorderete, abbiamo un tipo speciale: una progressione geometrica infinitamente decrescente. Come calcolare la somma dei suoi membri? E perché questo tipo di progressione ha determinate caratteristiche? Scopriamolo insieme.

Quindi, per cominciare, diamo un'occhiata a questa immagine di una progressione geometrica infinitamente decrescente dal nostro esempio:

E ora diamo un'occhiata alla formula per la somma di una progressione geometrica, derivata poco prima:
o

Per cosa ci stiamo battendo? Esatto, il grafico mostra che tende a zero. Cioè, quando sarà quasi uguale, rispettivamente, quando calcoliamo l'espressione, otterremo quasi. A questo proposito, riteniamo che nel calcolare la somma di una progressione geometrica infinitamente decrescente, questa parentesi possa essere trascurata, poiché sarà uguale.

- la formula è la somma dei termini di una progressione geometrica infinitamente decrescente.

IMPORTANTE! Usiamo la formula per la somma dei termini di una progressione geometrica infinitamente decrescente solo se la condizione afferma esplicitamente che dobbiamo trovare la somma senza fine il numero dei membri.

Se viene indicato un numero specifico n, utilizziamo la formula per la somma di n termini, anche se o.

E ora facciamo pratica.

Trova la somma dei primi termini di una progressione geometrica con e.
Trova la somma dei termini di una progressione geometrica infinitamente decrescente con e.

Spero tu sia stato molto attento. Confronta le nostre risposte:

Ora sai tutto sulla progressione geometrica ed è tempo di passare dalla teoria alla pratica. I problemi esponenziali più comuni riscontrati durante l'esame sono i problemi di interesse composto. È di loro che parleremo.

Problemi per il calcolo dell'interesse composto.

Devi aver sentito parlare della cosiddetta formula dell'interesse composto. Capisci cosa intende? Se no, scopriamolo, perché dopo aver realizzato il processo stesso, capirete subito cosa c'entra la progressione geometrica con esso.

Andiamo tutti in banca e sappiamo che ci sono condizioni diverse per i depositi: questo è il termine, e il mantenimento aggiuntivo, e gli interessi con due diversi modi di calcolarlo: semplice e complesso.

DA interesse semplice tutto è più o meno chiaro: gli interessi vengono addebitati una volta alla fine del termine di deposito. Cioè, se stiamo parlando di mettere sotto 100 rubli all'anno, verranno accreditati solo alla fine dell'anno. Di conseguenza, entro la fine del deposito, riceveremo rubli.

Interesse compostoè un'opzione in cui capitalizzazione di interessi, cioè. la loro aggiunta all'importo del deposito e il successivo calcolo del reddito non dall'iniziale, ma dall'importo accumulato del deposito. La capitalizzazione non avviene costantemente, ma con una certa periodicità. Di norma, tali periodi sono uguali e molto spesso le banche utilizzano un mese, un trimestre o un anno.

Diciamo che mettiamo tutti gli stessi rubli all'anno, ma con una capitalizzazione mensile del deposito. Cosa otteniamo?

Capisci tutto qui? In caso contrario, procediamo passo dopo passo.

Abbiamo portato i rubli in banca. Entro la fine del mese, dovremmo avere un importo sul nostro conto composto dai nostri rubli più gli interessi su di essi, ovvero:

Concordare?

Possiamo toglierlo dalla parentesi e quindi otteniamo:

D'accordo, questa formula è già più simile a quella che abbiamo scritto all'inizio. Resta da fare i conti con le percentuali

Nella condizione del problema, ci viene detto dell'annuale. Come sai, non moltiplichiamo per - convertiamo le percentuali in decimali, ovvero:

Destra? Ora chiedi, da dove viene il numero? Molto semplice!
Ripeto: dice la condizione del problema ANNUALE interessi maturati MENSILE. Come sapete, tra un anno di mesi, rispettivamente, la banca ci addebiterà una parte degli interessi annuali mensili:

Realizzato? Ora prova a scrivere come sarebbe questa parte della formula se dicessi che l'interesse viene calcolato giornalmente.
Sei riuscito? Confrontiamo i risultati:

Molto bene! Torniamo al nostro compito: scrivi quanto verrà accreditato sul nostro conto per il secondo mese, tenendo conto che sull'importo del deposito accumulato vengono addebitati gli interessi.
Ecco cosa mi è successo:

O, in altre parole:

Penso che tu abbia già notato uno schema e visto una progressione geometrica in tutto questo. Scrivi a cosa sarà uguale il suo membro, o, in altre parole, quanto denaro riceveremo alla fine del mese.
Fatto? Controllo!

Come puoi vedere, se metti denaro in banca per un anno con un interesse semplice, riceverai rubli e se lo metti a un tasso composto, riceverai rubli. Il vantaggio è piccolo, ma questo accade solo durante il esimo anno, ma per un periodo più lungo la capitalizzazione è molto più redditizia:

Considera un altro tipo di problemi di interesse composto. Dopo quello che hai capito, sarà elementare per te. Quindi il compito è:

Zvezda ha iniziato a investire nel settore nel 2000 con un capitale in dollari. Ogni anno dal 2001 ha realizzato un utile pari al capitale dell'anno precedente. Quanto profitto riceverà la società Zvezda alla fine del 2003, se l'utile non sarà ritirato dalla circolazione?

La capitale della società Zvezda nel 2000.
- il capitale della società Zvezda nel 2001.
- il capitale della società Zvezda nel 2002.
- il capitale della società Zvezda nel 2003.

Oppure possiamo scrivere brevemente:

Per il nostro caso:

2000, 2001, 2002 e 2003.

Rispettivamente:
rubli
Si noti che in questo problema non abbiamo una divisione né per né per, poiché la percentuale è data ANNUALMENTE e viene calcolata ANNUALMENTE. Cioè, quando leggi il problema per l'interesse composto, presta attenzione a quale percentuale viene data e in quale periodo viene addebitata, e solo allora procedi ai calcoli.
Ora sai tutto sulla progressione geometrica.

Formazione.

Trova un termine di una progressione geometrica se è noto che, e
Trova la somma dei primi termini di una progressione geometrica, se è noto, e
MDM Capital ha iniziato a investire nel settore nel 2003 con un capitale in dollari. Ogni anno dal 2004 ha realizzato un profitto pari al capitale dell'anno precedente. La società "MSK Cash Flows" ha iniziato a investire nel settore nel 2005 per un importo di $ 10.000, iniziando a realizzare un profitto nel 2006 per un importo di. Di quanti dollari il capitale di una società supera quello di un'altra alla fine del 2007, se gli utili non sono stati ritirati dalla circolazione?

Risposte:

Poiché la condizione del problema non dice che la progressione è infinita ed è necessario trovare la somma di un determinato numero dei suoi membri, il calcolo viene effettuato secondo la formula:
Società "MDM Capital":
2003, 2004, 2005, 2006, 2007.
- aumenta del 100%, ovvero 2 volte.
Rispettivamente:
rubli
Flussi di cassa MSK:
2005, 2006, 2007.
- aumenta di, cioè, volte.
Rispettivamente:
rubli
rubli

Riassumiamo.

1) Una progressione geometrica ( ) è una sequenza numerica, il cui primo termine è diverso da zero, e ogni termine, a partire dal secondo, è uguale al precedente, moltiplicato per lo stesso numero. Questo numero è chiamato denominatore di una progressione geometrica.

2) L'equazione delle membra di una progressione geometrica -.

3) può assumere qualsiasi valore, ad eccezione di e.

se, allora tutti i membri successivi della progressione hanno lo stesso segno - loro positivo;
se, allora tutti i membri successivi della progressione segni alternativi;
at - la progressione è chiamata infinitamente decrescente.

4), at è una proprietà di una progressione geometrica (membri vicini)

o
, a (termini equidistanti)

Quando lo trovi, non dimenticarlo dovrebbero esserci due risposte..

Per esempio,

5) La somma dei membri di una progressione geometrica si calcola con la formula:
o

IMPORTANTE! Usiamo la formula per la somma dei termini di una progressione geometrica infinitamente decrescente solo se la condizione afferma esplicitamente che è necessario trovare la somma di un numero infinito di termini.

6) Gli incarichi per interesse composto sono calcolati anche secondo la formula del esimo membro di una progressione geometrica, purché i fondi non siano stati ritirati dalla circolazione:

PROGRESSIONE GEOMETRICA. IN BREVE SUL PRINCIPALE

Progressione geometrica( ) è una sequenza numerica, il cui primo termine è diverso da zero, e ogni termine, a partire dal secondo, è uguale al precedente, moltiplicato per lo stesso numero. Questo numero è chiamato denominatore di una progressione geometrica.

Denominatore di una progressione geometrica può assumere qualsiasi valore tranne e.

Se, tutti i membri successivi della progressione hanno lo stesso segno, sono positivi;
se, allora tutti i successivi membri della progressione si alternano di segno;
at - la progressione è chiamata infinitamente decrescente.

Equazione delle membra di una progressione geometrica - .

La somma dei termini di una progressione geometrica calcolato con la formula:
o

Se la progressione è infinitamente decrescente, allora:

I 2/3 ARTICOLI RESTANTI SONO DISPONIBILI SOLO PER YOUCLEVER STUDENTI!

Diventa uno studente di YouClever,

Preparati per l'OGE o USE in matematica al prezzo di "una tazza di caffè al mese",

E ottieni anche accesso illimitato al libro di testo "YouClever", al programma di formazione "100gia" (libro delle soluzioni), USE e OGE di prova illimitati, 6000 attività con analisi delle soluzioni e altri servizi YouClever e 100gia.

Una progressione geometrica è una sequenza numerica il cui primo termine è diverso da zero e ogni termine successivo è uguale al termine precedente moltiplicato per lo stesso numero diverso da zero. La progressione geometrica è indicata da b1,b2,b3, …, bn, …

Proprietà di una progressione geometrica

Il rapporto di qualsiasi termine dell'errore geometrico con il suo termine precedente è uguale allo stesso numero, cioè b2/b1 = b3/b2 = b4/b3 = … = bn/b(n-1) = b(n+ 1)/mld = …. Ciò deriva direttamente dalla definizione di progressione aritmetica. Questo numero è chiamato denominatore di una progressione geometrica. Solitamente il denominatore di una progressione geometrica è indicato dalla lettera q.

Un modo per impostare una progressione geometrica consiste nell'impostare il suo primo termine b1 e il denominatore dell'errore geometrico q. Ad esempio, b1=4, q=-2. Queste due condizioni danno una progressione geometrica di 4, -8, 16, -32, … .

Se q>0 (q non è uguale a 1), allora la progressione è sequenza monotona. Ad esempio, la sequenza 2, 4,8,16,32, ... è una sequenza monotonicamente crescente (b1=2, q=2).

Se il denominatore q=1 nell'errore geometrico, allora tutti i membri della progressione geometrica saranno uguali tra loro. In questi casi, si dice che la progressione è una sequenza costante.

Formula dell'ennesimo membro della progressione

Affinché la sequenza numerica (bn) sia una progressione geometrica, è necessario che ciascuno dei suoi membri, a partire dal secondo, sia la media geometrica degli elementi vicini. Cioè, è necessario soddisfare la seguente equazione - (b(n+1))^2 = bn * b(n+2), per ogni n>0, dove n appartiene all'insieme numeri naturali N.

La formula per l'ennesimo membro di una progressione geometrica è:

bn=b1*q^(n-1), dove n appartiene all'insieme dei numeri naturali N.

Considera un semplice esempio:

In progressione geometrica b1=6, q=3, n=8 trova bn.

Usiamo la formula dell'n-esimo membro di una progressione geometrica.

Lezione correlata “Progressione geometrica infinitamente decrescente”

Lo scopo della lezione: introducendo gli studenti a un nuovo tipo di sequenza: una progressione geometrica infinitamente decrescente.

Compiti:

formulazione dell'idea iniziale del limite della sequenza numerica; conoscenza di un altro modo per convertire infinite frazioni periodiche in ordinarie usando la formula per la somma di una progressione geometrica infinitamente decrescente;

sviluppo delle qualità intellettuali della personalità degli scolari, come ad esempio pensiero logico, la capacità di azioni valutative, la generalizzazione;

educazione all'attività, mutua assistenza, collettivismo, interesse per la materia.

Attrezzatura: lezione di computer, proiettore, schermo.

Tipo di lezione: lezione - apprendimento nuovo argomento.

Durante le lezioni

io . Org. momento. Messaggio sull'argomento e lo scopo della lezione.

II . Aggiornare le conoscenze degli studenti.1. Controllo dei compiti.

1) Verifica delle formule di base relative alle progressioni aritmetiche e geometriche. Due studenti scrivono le formule alla lavagna.

2) Il resto degli studenti sì dettatura matematica sull'argomento "Formule di somma".

Compiti:

№1. Trova la somma dei primi cinque membri di una progressione aritmetica se il suo primo membro è 6 (1a opzione), -20 (2a opzione) e il quinto membro è -6 (1a opzione), 20 (2a opzione).

№2. Trova la somma dei primi cinque termini di una progressione aritmetica se il suo primo termine è -20(1a opzione), 6(2a opzione) e la differenza è 10(1a opzione), -3(2a opzione).

№3. Trova la somma dei primi cinque termini di una progressione geometrica se il suo primo termine è 1(1a opzione), -1 (2a opzione) e il denominatore è -2(1a opzione), 2(2a opzione).

Al termine del dettato, selettivamente, il lavoro di due studenti viene verificato per la valutazione, gli altri effettuano l'autoesame secondo soluzioni chiavi in mano scritto sui risvolti della tavola.

Soluzioni:

Compiti

1. La progressione aritmetica è data dalla formula un n = 7 – 4 n. Trovare un 10 . (-33)

2. Progressione aritmetica un 3 = 7 e un 5 = 1 . Trovare un 4 . (4)

3. Progressione aritmetica un 3 = 7 e un 5 = 1 . Trovare un 17 . (-35)

4. Progressione aritmetica un 3 = 7 e un 5 = 1 . Trovare S 17 . (-187)

5. Per una progressione geometrica
trova il quinto termine.

6. Per una progressione geometrica
trovare n-esimo membro.

7. In modo esponenziale B 3 = 8 e B 5 = 2 . Trovare B 4 . (4)

8. In modo esponenziale B 3 = 8 e B 5 = 2 . Trovare B 1 e Q .

9. In modo esponenziale B 3 = 8 e B 5 = 2 . Trovare S 5 . (62)

III . Esplorare un nuovo argomento(presentazione dimostrativa).

Consideriamo un quadrato con lato uguale a 1. Disegniamo un altro quadrato, il cui lato è metà del primo quadrato, poi un altro, il cui lato è metà del secondo, poi il successivo e così via. Ogni volta il lato del nuovo quadrato è la metà del precedente.

Di conseguenza, abbiamo ottenuto una sequenza di lati di quadrati formando una progressione geometrica con denominatore.

E, cosa molto importante, più costruiamo tali quadrati, più piccolo sarà il lato del quadrato. Per esempio,

Quelli. all'aumentare del numero n, i termini della progressione si avvicinano a zero.

Con l'aiuto di questa figura, è possibile considerare un'altra sequenza.

Ad esempio, la sequenza delle aree dei quadrati:

. E, ancora, se n aumenta indefinitamente, quindi l'area si avvicina allo zero arbitrariamente vicino.

Consideriamo un altro esempio. Un triangolo equilatero di lato 1 cm. Costruiamo il prossimo triangolo con i vertici ai punti medi dei lati del 1° triangolo, secondo il teorema su linea di mezzo triangolo: il lato del 2° è uguale alla metà del lato del primo, il lato del 3° è metà del lato del 2°, ecc. Ancora una volta otteniamo una sequenza di lunghezze dei lati dei triangoli.

a
.

Se consideriamo una progressione geometrica con denominatore negativo.

Poi, ancora, con numeri crescenti n i termini della progressione si avvicinano a zero.

Prestiamo attenzione ai denominatori di queste sequenze. Ovunque i denominatori erano inferiori a 1 modulo.

Possiamo concludere: una progressione geometrica sarà infinitamente decrescente se il modulo del suo denominatore è minore di 1.

Lavoro frontale.

Definizione:

Una progressione geometrica si dice infinitamente decrescente se il modulo del suo denominatore è minore di uno.
.

Con l'aiuto della definizione, è possibile risolvere la questione se una progressione geometrica sia infinitamente decrescente o meno.

Un compito

La successione è una progressione geometrica infinitamente decrescente se è data dalla formula:

;
.

Soluzione:

. Cerchiamo Q .

;
;
;
.

questa progressione geometrica è infinitamente decrescente.

B) questa sequenza non è una progressione geometrica infinitamente decrescente.

Considera un quadrato di lato uguale a 1. Dividilo a metà, una delle metà ancora a metà e così via. le aree di tutti i rettangoli risultanti formano una progressione geometrica infinitamente decrescente:

La somma delle aree di tutti i rettangoli così ottenuti sarà uguale all'area del 1° quadrato e uguale a 1.

Ma sul lato sinistro di questa uguaglianza c'è la somma di un numero infinito di termini.

Considera la somma dei primi n termini.

Secondo la formula per la somma dei primi n termini di una progressione geometrica, è uguale a .

Se n aumenta indefinitamente, quindi

o
. Ecco perché
, cioè.
.

La somma di una progressione geometrica infinitamente decrescente c'è un limite di sequenza S 1 , S 2 , S 3 , …, S n , … .

Ad esempio, per una progressione
,

Perché

La somma di una progressione geometrica infinitamente decrescente può essere trovato usando la formula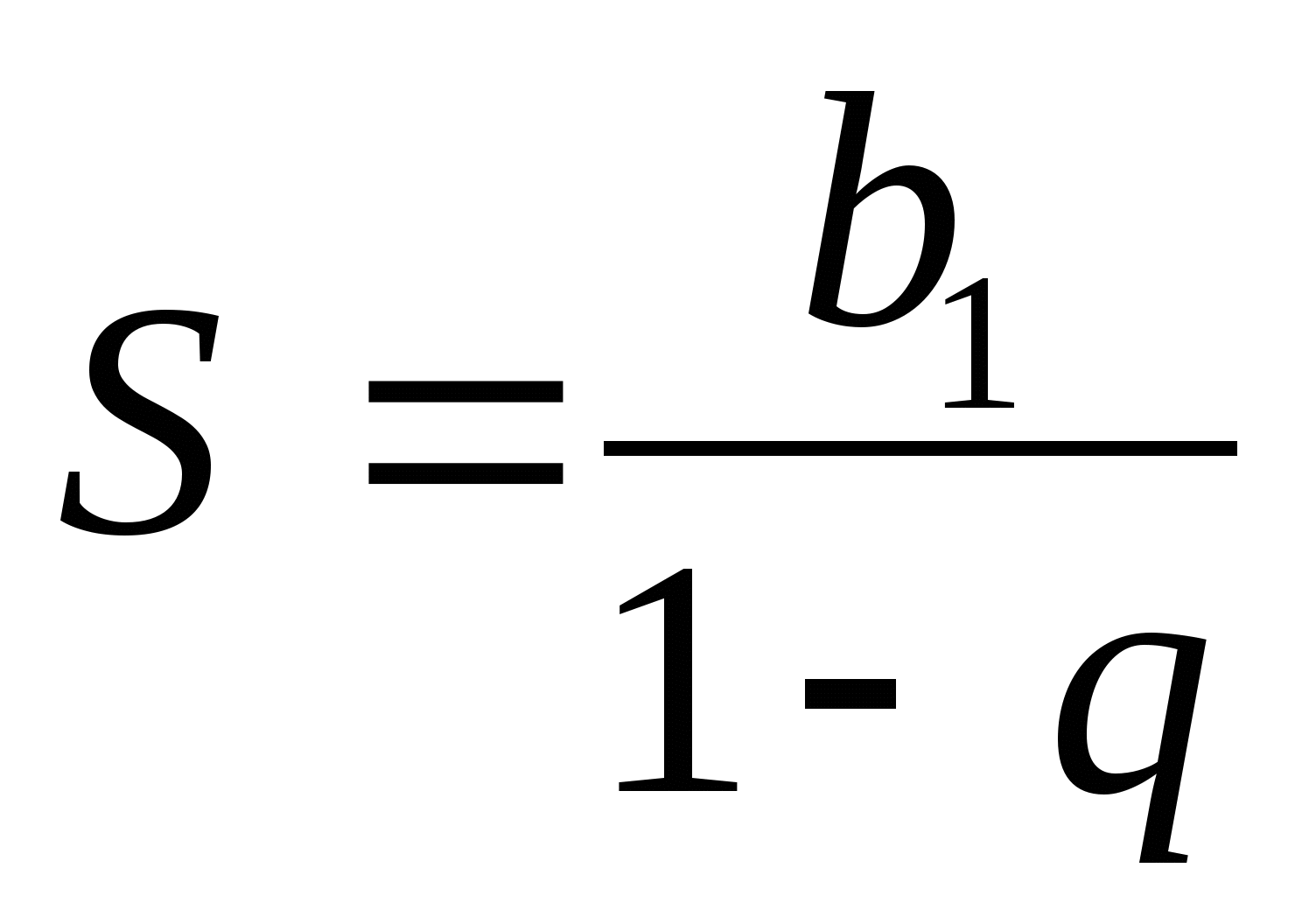
.

III . Riflessione e consolidamento(completamento dei compiti).

Compito numero 2. Trova la somma di una progressione geometrica infinitamente decrescente con il primo termine 3, il secondo 0,3.

Soluzione:

Compito numero 3. libro di testo, pagina 160, n. 433(1)

Trova la somma di una progressione geometrica infinitamente decrescente:

Soluzione:

Compito numero 4. Scrivi un periodico infinito decimale 0,(5) come frazione ordinaria.

1a via. Sia x = 0, (5) = 0,555 ... / 10 2° metodo. 0,(5)=0,555…=

Compito numero 5. libro di testo, p. 162, n. 445(3) ( decisione indipendente)

Scrivi la frazione decimale periodica infinita 0,(12) come frazione comune.

Risposta: 0,(12)=4/33.

IV . Riassumendo.

Che sequenza hai incontrato oggi?

Definire una progressione geometrica infinitamente decrescente.

Come dimostrare che una progressione geometrica è infinitamente decrescente?

Dare la formula per la somma di una progressione geometrica infinitamente decrescente.

v . Compiti a casa.

Si indica la progressione geometrica b1,b2,b3, …, bn, … .

Sequenza monotona e costante

Se q>0 (q non è uguale a 1), allora la progressione è sequenza monotona. Ad esempio, la sequenza 2, 4,8,16,32, ... è una sequenza monotonicamente crescente (b1=2, q=2).

Se il denominatore q=1 nell'errore geometrico, allora tutti i membri della progressione geometrica saranno uguali tra loro. In questi casi, si dice che la progressione sia sequenza costante.

Formula dell'ennesimo membro di una progressione geometrica

Affinché la sequenza numerica (bn) sia una progressione geometrica, è necessario che ciascuno dei suoi membri, a partire dal secondo, sia la media geometrica degli elementi vicini. Cioè, è necessario soddisfare la seguente equazione
(b(n+1))^2 = bn * b(n+2), per ogni n>0, dove n appartiene all'insieme dei numeri naturali N.

La formula per l'ennesimo membro di una progressione geometrica è:

bn=b1*q^(n-1),

dove n appartiene all'insieme dei numeri naturali N.

La formula per la somma dei primi n termini di una progressione geometrica

La formula per la somma dei primi n termini di una progressione geometrica è:

Sn = (bn*q - b1)/(q-1) dove q non è uguale a 1.

Considera un semplice esempio:

In progressione geometrica b1=6, q=3, n=8 trova Sn.

Per trovare S8 utilizziamo la formula per la somma dei primi n termini di una progressione geometrica.

S8= (6*(3^8 -1))/(3-1) = 19680.