Funcțiile elementare de bază, proprietățile lor inerente și graficele corespunzătoare sunt unul dintre bazele cunoștințelor matematice, similare ca importanță cu tabelul înmulțirii. Funcțiile elementare sunt baza, suportul pentru studiul tuturor problemelor teoretice.

Articolul de mai jos oferă material cheie pe tema funcțiilor elementare de bază. Vom introduce termeni, le vom da definiții; Să studiem în detaliu fiecare tip de funcții elementare și să le analizăm proprietățile.

Se disting următoarele tipuri de funcții elementare de bază:

Definiția 1

• funcție constantă (constant);
• rădăcina gradului al n-lea;
• funcția de putere;
• functie exponentiala;
• funcția logaritmică;
• funcții trigonometrice;
• funcții trigonometrice fraterne.

O funcție constantă este definită prin formula: y = C (C este un număr real) și are, de asemenea, un nume: constantă. Această funcție determină dacă orice valoare reală a variabilei independente x corespunde aceleiași valori a variabilei y – valoarea C .

Graficul unei constante este o dreaptă care este paralelă cu axa x și trece printr-un punct având coordonatele (0, C). Pentru claritate, prezentăm grafice ale funcțiilor constante y = 5 , y = - 2 , y = 3 , y = 3 (marcate cu negru, roșu și, respectiv, albastru în desen).

Definiția 2

Această funcție elementară este definită de formula y = x n (n - numar natural mai mult de o).

Să luăm în considerare două variante ale funcției.

1. Rădăcina de gradul al n-lea, n este un număr par

Pentru claritate, indicăm desenul, care arată graficele unor astfel de funcții: y = x , y = x 4 și y = x 8 . Aceste funcții sunt codate pe culori: negru, roșu și, respectiv, albastru.

O vedere similară a graficelor funcției de un grad par pentru alte valori ale indicatorului.

Definiția 3

Proprietăți ale funcției rădăcină de gradul al n-lea, n este un număr par

• domeniul definirii este multimea tuturor nenegativelor numere reale [ 0 , + ∞) ;
• când x = 0, funcția y = x n are o valoare egală cu zero;
• această funcție este o funcție vedere generala(nu este nici par, nici impar);
• interval: [ 0 , + ∞) ;
• această funcție y = x n cu exponenți pari ai rădăcinii crește pe întregul domeniu de definiție;
• funcția are o convexitate cu direcție ascendentă pe întregul domeniu de definiție;
• nu există puncte de inflexiune;
• nu există asimptote;
• graficul funcției pentru n par trece prin punctele (0 ; 0) și (1 ; 1) .

1. Rădăcina de gradul al n-lea, n este un număr impar

O astfel de funcție este definită pe întregul set de numere reale. Pentru claritate, luați în considerare graficele funcțiilor y = x 3 , y = x 5 și x 9 . În desen, acestea sunt indicate prin culori: culorile negru, roșu și albastru ale curbelor, respectiv.

Alte valori impare ale exponentului rădăcinii funcției y = x n vor da un grafic de formă similară.

Definiția 4

Proprietăți ale funcției rădăcină de gradul al n-lea, n este un număr impar

• domeniul definiției este mulțimea tuturor numerelor reale;
• această funcție este impară;
• intervalul de valori este mulțimea tuturor numerelor reale;
• funcția y = x n cu exponenți impari ai rădăcinii crește pe întregul domeniu de definiție;
• funcția are concavitate pe intervalul (- ∞ ; 0 ] și convexitate pe intervalul [ 0 , + ∞) ;
• punctul de inflexiune are coordonatele (0 ; 0) ;
• nu există asimptote;
• graficul funcției pentru n impar trece prin punctele (- 1 ; - 1) , (0 ; 0) și (1 ; 1) .

Funcția de putere

Definiția 5

Funcția de putere este definită de formula y = x a .

Tipul de grafice și proprietățile funcției depind de valoarea exponentului.

• când o funcție de putere are un exponent întreg a, atunci forma graficului funcției de putere și proprietățile acesteia depind de dacă exponentul este par sau impar și, de asemenea, ce semn are exponentul. Să luăm în considerare toate aceste cazuri speciale mai detaliat mai jos;
• exponentul poate fi fracționar sau irațional - în funcție de aceasta, variază și tipul de grafice și proprietățile funcției. Vom analiza cazuri speciale prin stabilirea mai multor condiții: 0< a < 1 ; a > 1 ; - 1 < a < 0 и a < - 1 ;
• o funcție de putere poate avea un exponent zero, vom analiza și acest caz mai detaliat mai jos.

Să analizăm funcția de putere y = x a când a este impar număr pozitiv, de exemplu, a = 1 , 3 , 5 ...

Pentru claritate, indicăm graficele unor astfel de funcții de putere: y = x (culoarea neagră a graficului), y = x 3 (culoarea albastră a graficului), y = x 5 (culoarea roșie a graficului), y = x 7 (graficul verde). Când a = 1 , obținem o funcție liniară y = x .

Definiția 6

Proprietățile unei funcții de putere atunci când exponentul este un pozitiv impar

• funcția este crescătoare pentru x ∈ (- ∞ ; + ∞) ;
• funcția este convexă pentru x ∈ (- ∞ ; 0 ] și concavă pentru x ∈ [ 0 ; + ∞) (excluzând funcția liniară);
• punctul de inflexiune are coordonatele (0 ; 0) (excluzând funcția liniară);
• nu există asimptote;
• funcția puncte de trecere: (- 1 ; - 1) , (0 ; 0) , (1 ; 1) .

Să analizăm funcția de putere y = x a când a este un număr pozitiv par, de exemplu, a = 2 , 4 , 6 ...

Pentru claritate, indicăm graficele unor astfel de funcții de putere: y \u003d x 2 (culoarea neagră a graficului), y = x 4 (culoarea albastră a graficului), y = x 8 (culoarea roșie a graficului). Când a = 2, obținem o funcție pătratică al cărei grafic este o parabolă pătratică.

Definiția 7

Proprietățile unei funcții de putere atunci când exponentul este chiar pozitiv:

• domeniu de definiție: x ∈ (- ∞ ; + ∞) ;
• descrescătoare pentru x ∈ (- ∞ ; 0 ] ;
• funcția este concavă pentru x ∈ (- ∞ ; + ∞) ;
• nu există puncte de inflexiune;
• nu există asimptote;
• puncte de trecere a funcției: (- 1 ; 1) , (0 ; 0) , (1 ; 1) .

Figura de mai jos prezintă exemple de grafice cu funcții exponențiale y = x a când a este un număr negativ impar: y = x - 9 (culoarea neagră a graficului); y = x - 5 (culoarea albastră a graficului); y = x - 3 (culoarea roșie a diagramei); y = x - 1 (graficul verde). Când a \u003d - 1, obținem o proporționalitate inversă, al cărei grafic este o hiperbolă.

Definiția 8

Proprietățile funcției de putere atunci când exponentul este impar negativ:

Când x \u003d 0, obținem o discontinuitate de al doilea fel, deoarece lim x → 0 - 0 xa \u003d - ∞, lim x → 0 + 0 xa \u003d + ∞ pentru a \u003d - 1, - 3, - 5, .... Astfel, linia dreaptă x = 0 este o asimptotă verticală;

• interval: y ∈ (- ∞ ; 0) ∪ (0 ; + ∞) ;
• funcția este impară deoarece y (- x) = - y (x) ;
• funcţia este descrescătoare pentru x ∈ - ∞ ; 0 ∪ (0 ; + ∞) ;
• funcția este convexă pentru x ∈ (- ∞ ; 0) și concavă pentru x ∈ (0 ; + ∞) ;
• nu există puncte de inflexiune;

k = lim x → ∞ x a x = 0 , b = lim x → ∞ (x a - k x) = 0 ⇒ y = k x + b = 0 când a = - 1 , - 3 , - 5 , . . . .

• funcția puncte de trecere: (- 1 ; - 1) , (1 ; 1) .

Figura de mai jos prezintă exemple de grafice ale funcției de putere y = x a când a este un număr negativ par: y = x - 8 (diagrama cu negru); y = x - 4 (culoarea albastră a graficului); y = x - 2 (culoarea roșie a graficului).

Definiția 9

Proprietățile funcției de putere atunci când exponentul este chiar negativ:

• domeniu de definiție: x ∈ (- ∞ ; 0) ∪ (0 ; + ∞) ;

Când x \u003d 0, obținem o discontinuitate de al doilea fel, deoarece lim x → 0 - 0 xa \u003d + ∞, lim x → 0 + 0 xa \u003d + ∞ pentru a \u003d - 2, - 4, - 6, .... Astfel, linia dreaptă x = 0 este o asimptotă verticală;

• funcția este pară deoarece y (- x) = y (x) ;
• funcția este crescătoare pentru x ∈ (- ∞ ; 0) și descrescătoare pentru x ∈ 0 ; +∞ ;
• funcția este concavă pentru x ∈ (- ∞ ; 0) ∪ (0 ; + ∞) ;
• nu există puncte de inflexiune;
• asimptota orizontală este o linie dreaptă y = 0 deoarece:

k = lim x → ∞ x a x = 0 , b = lim x → ∞ (x a - k x) = 0 ⇒ y = k x + b = 0 când a = - 2 , - 4 , - 6 , . . . .

• funcția puncte de trecere: (- 1 ; 1) , (1 ; 1) .

Încă de la început, acordați atenție următorului aspect: în cazul în care a este o fracție pozitivă cu numitor impar, unii autori iau intervalul - ∞ ca domeniu de definiție al acestei funcții de putere; + ∞ , stipulând că exponentul a este o fracție ireductibilă. În acest moment, autorii multor publicații educaționale despre algebră și începuturile analizei NU DEFINEȘTE funcții de putere, unde exponentul este o fracție cu un numitor impar pentru valorile negative ale argumentului. Mai departe, vom adera la o astfel de poziție: luăm setul [ 0 ; +∞). Recomandare pentru elevi: aflați punctul de vedere al profesorului în acest moment pentru a evita neînțelegerile.

Deci, să aruncăm o privire la funcția de putere y = x a când exponentul este un număr rațional sau irațional cu condiția ca 0< a < 1 .

Să ilustrăm cu grafice funcțiile de putere y = x a când a = 11 12 (diagrama cu negru); a = 5 7 (culoarea roșie a graficului); a = 1 3 (culoarea albastră a graficului); a = 2 5 (culoarea verde a graficului).

Alte valori ale exponentului a (presupunând 0< a < 1) дадут аналогичный вид графика.

Definiția 10

Proprietățile funcției de putere la 0< a < 1:

• interval: y ∈ [ 0 ; +∞) ;
• funcţia este crescătoare pentru x ∈ [ 0 ; +∞) ;
• funcția are convexitate pentru x ∈ (0 ; + ∞) ;
• nu există puncte de inflexiune;
• nu există asimptote;

Să analizăm funcția de putere y = x a când exponentul este un număr rațional sau irațional neîntreg cu condiția ca a > 1 .

Ilustram graficele functiei putere y \u003d xa în condiții date, folosind următoarele funcții ca exemplu: y \u003d x 5 4, y \u003d x 4 3, y \u003d x 7 3, y \u003d x 3 π (negru, roșu, albastru, verde grafice, respectiv).

Alte valori ale exponentului a cu condiția a > 1 vor oferi o vedere similară a graficului.

Definiția 11

Proprietățile funcției de putere pentru a > 1:

• domeniu de definire: x ∈ [ 0 ; +∞) ;
• interval: y ∈ [ 0 ; +∞) ;
• această funcție este o funcție de formă generală (nu este nici impar, nici par);
• funcţia este crescătoare pentru x ∈ [ 0 ; +∞) ;
• funcția este concavă pentru x ∈ (0 ; + ∞) (când 1< a < 2) и выпуклость при x ∈ [ 0 ; + ∞) (когда a > 2);
• nu există puncte de inflexiune;
• nu există asimptote;
• funcția puncte de trecere: (0 ; 0) , (1 ; 1) .

Vă atragem atenția! Când a este o fracție negativă cu un numitor impar, în lucrările unor autori există opinia că domeniul de definiție în acest caz este intervalul - ∞; 0 ∪ (0 ; + ∞) cu condiția ca exponentul a să fie o fracție ireductibilă. În acest moment autorii materiale didactice conform algebrei și începuturilor analizei, funcțiile de putere cu exponent sub forma unei fracții cu numitor impar cu valori negative ale argumentului NU sunt DEFINITE. Mai mult, aderăm la o astfel de vedere: luăm mulțimea (0 ; + ∞) ca domeniu al funcțiilor de putere cu exponenți negativi fracționari. Sugestie pentru elevi: clarificați viziunea profesorului în acest moment pentru a evita dezacordul.

Continuăm subiectul și analizăm funcția de putere y = x a cu condiția: - 1< a < 0 .

Iată un desen cu grafice următoarele caracteristici: y = x - 5 6 , y = x - 2 3 , y = x - 1 2 2 , y = x - 1 7 (respectiv linii negre, roșii, albastre, verzi).

Definiția 12

Proprietățile funcției de putere la - 1< a < 0:

lim x → 0 + 0 x a = + ∞ când - 1< a < 0 , т.е. х = 0 – вертикальная асимптота;

• interval: y ∈ 0 ; +∞ ;
• această funcție este o funcție de formă generală (nu este nici impar, nici par);
• nu există puncte de inflexiune;

Desenul de mai jos prezintă grafice ale funcțiilor de putere y = x - 5 4 , y = x - 5 3 , y = x - 6 , y = x - 24 7 (negru, roșu, albastru, culori verzi curbe, respectiv).

Definiția 13

Proprietățile funcției de putere pentru a< - 1:

• domeniu de definire: x ∈ 0 ; +∞ ;

lim x → 0 + 0 x a = + ∞ când a< - 1 , т.е. х = 0 – вертикальная асимптота;

• interval: y ∈ (0 ; + ∞) ;
• această funcție este o funcție de formă generală (nu este nici impar, nici par);
• funcția este descrescătoare pentru x ∈ 0; +∞ ;
• funcția este concavă pentru x ∈ 0; +∞ ;
• nu există puncte de inflexiune;
• asimptotă orizontală - linie dreaptă y = 0 ;
• punct de trecere a funcției: (1 ; 1) .

Când a \u003d 0 și x ≠ 0, obținem funcția y \u003d x 0 \u003d 1, care determină linia din care este exclus punctul (0; 1) (am convenit că expresia 0 0 nu va fi dată orice valoare).

Funcția exponențială are forma y = a x , unde a > 0 și a ≠ 1 , iar graficul acestei funcții arată diferit în funcție de valoarea bazei a . Să luăm în considerare cazurile speciale.

Să luăm în considerare mai întâi situația în care baza functie exponentiala are o valoare de la zero la unu (0< a < 1) . Un exemplu ilustrativ sunt graficele funcțiilor pentru a = 1 2 (culoarea albastră a curbei) și a = 5 6 (culoarea roșie a curbei).

Graficele funcției exponențiale vor avea o formă similară pentru alte valori ale bazei, cu condiția ca 0< a < 1 .

Definiția 14

Proprietățile unei funcții exponențiale când baza este mai mică de unu:

• interval: y ∈ (0 ; + ∞) ;
• această funcție este o funcție de formă generală (nu este nici impar, nici par);
• o funcție exponențială a cărei bază este mai mică de unu este în scădere pe întregul domeniu de definiție;
• nu există puncte de inflexiune;
• asimptota orizontală este dreapta y = 0 cu variabila x tinde spre + ∞ ;

Acum luați în considerare cazul în care baza funcției exponențiale este mai mare decât unu (a > 1).

Să ilustrăm acest caz special cu graficul funcțiilor exponențiale y = 3 2 x (culoarea albastră a curbei) și y = e x (culoarea roșie a graficului).

Alte valori ale bazei, mai mari decât unu, vor oferi o vedere similară a graficului funcției exponențiale.

Definiția 15

Proprietățile funcției exponențiale când baza este mai mare decât unu:

• domeniul de definiție este întregul set de numere reale;
• interval: y ∈ (0 ; + ∞) ;
• această funcție este o funcție de formă generală (nu este nici impar, nici par);
• o funcţie exponenţială a cărei bază este mai mare decât unu este crescătoare pentru x ∈ - ∞ ; +∞ ;
• funcţia este concavă pentru x ∈ - ∞ ; +∞ ;
• nu există puncte de inflexiune;
• asimptotă orizontală - dreaptă y = 0 cu variabila x tinde spre - ∞ ;
• punct de trecere a funcției: (0 ; 1) .

Funcția logaritmică are forma y = log a (x) , unde a > 0 , a ≠ 1 .

O astfel de funcție este definită numai pentru valorile pozitive ale argumentului: pentru x ∈ 0 ; +∞ .

Graficul funcției logaritmice are o formă diferită, în funcție de valoarea bazei a.

Luați în considerare mai întâi situația când 0< a < 1 . Продемонстрируем этот частный случай графиком логарифмической функции при a = 1 2 (синий цвет кривой) и а = 5 6 (красный цвет кривой).

Alte valori ale bazei, nu mai mari de unu, vor oferi o vedere similară a graficului.

Definiția 16

Proprietățile unei funcții logaritmice când baza este mai mică de unu:

• domeniu de definire: x ∈ 0 ; +∞ . Deoarece x tinde spre zero din dreapta, valorile funcției tind spre + ∞;
• interval: y ∈ - ∞ ; +∞ ;
• această funcție este o funcție de formă generală (nu este nici impar, nici par);
• logaritmică
• funcția este concavă pentru x ∈ 0; +∞ ;
• nu există puncte de inflexiune;
• nu există asimptote;

Acum să analizăm un caz special când baza funcției logaritmice este mai mare decât unu: a > 1 . În desenul de mai jos, există grafice ale funcțiilor logaritmice y = log 3 2 x și y = ln x (culorile albastru și, respectiv, roșu ale graficelor).

Alte valori ale bazei mai mari decât unu vor oferi o vedere similară a graficului.

Definiția 17

Proprietățile unei funcții logaritmice când baza este mai mare decât unu:

• domeniu de definire: x ∈ 0 ; +∞ . Deoarece x tinde spre zero din dreapta, valorile funcției tind spre - ∞;
• interval: y ∈ - ∞ ; + ∞ (întregul set de numere reale);
• această funcție este o funcție de formă generală (nu este nici impar, nici par);
• funcția logaritmică este crescătoare pentru x ∈ 0; +∞ ;
• funcția are convexitate pentru x ∈ 0; +∞ ;
• nu există puncte de inflexiune;
• nu există asimptote;
• punct de trecere a funcției: (1 ; 0) .

Funcțiile trigonometrice sunt sinus, cosinus, tangentă și cotangentă. Să analizăm proprietățile fiecăruia dintre ele și graficele corespunzătoare.

În general, toate funcțiile trigonometrice sunt caracterizate de proprietatea periodicității, adică. când valorile funcției se repetă la sensuri diferite argument, care diferă unul de celălalt prin valoarea perioadei f (x + T) = f (x) (T este perioada). Astfel, elementul „perioada cea mai mică pozitivă” este adăugat la lista de proprietăți ale funcțiilor trigonometrice. În plus, vom indica astfel de valori ale argumentului pentru care funcția corespunzătoare dispare.

1. Funcția sinus: y = sin(x)

Graficul acestei funcții se numește undă sinusoidală.

Definiția 18

Proprietățile funcției sinus:

• domeniu de definiție: întreaga mulțime de numere reale x ∈ - ∞ ; +∞ ;
• funcția dispare când x = π k , unde k ∈ Z (Z este mulțimea numerelor întregi);
• funcția este crescătoare pentru x ∈ - π 2 + 2 π · k ; π 2 + 2 π k , k ∈ Z și descrescătoare pentru x ∈ π 2 + 2 π k ; 3 π 2 + 2 π k , k ∈ Z ;
• functia sinus are maxime localeîn punctele π 2 + 2 π · k ; 1 și minime locale în puncte - π 2 + 2 π · k ; - 1 , k ∈ Z ;
• funcția sinus este concavă când x ∈ - π + 2 π k; 2 π k , k ∈ Z și convex când x ∈ 2 π k ; π + 2 π k , k ∈ Z ;
• nu există asimptote.

1. functia cosinus: y=cos(x)

Graficul acestei funcții se numește undă cosinus.

Definiția 19

Proprietățile funcției cosinus:

• domeniu de definire: x ∈ - ∞ ; +∞ ;
• cea mai mică perioadă pozitivă: T \u003d 2 π;
• interval: y ∈ - 1 ; unu ;
• această funcție este pară, deoarece y (- x) = y (x) ;
• funcția este crescătoare pentru x ∈ - π + 2 π · k ; 2 π · k , k ∈ Z și descrescătoare pentru x ∈ 2 π · k ; π + 2 π k , k ∈ Z ;
• funcţia cosinus are maxime locale în punctele 2 π · k ; 1 , k ∈ Z și minime locale în punctele π + 2 π · k ; - 1 , k ∈ z ;
• funcția cosinus este concavă când x ∈ π 2 + 2 π · k ; 3 π 2 + 2 π k , k ∈ Z și convex când x ∈ - π 2 + 2 π k ; π 2 + 2 π · k , k ∈ Z ;
• punctele de inflexiune au coordonatele π 2 + π · k ; 0 , k ∈ Z
• nu există asimptote.

1. Funcția tangentă: y = t g (x)

Graficul acestei funcții se numește tangentoid.

Definiția 20

Proprietățile funcției tangente:

• domeniu de definiție: x ∈ - π 2 + π · k ; π 2 + π k , unde k ∈ Z (Z este mulțimea numerelor întregi);
• Comportarea funcției tangente la limita domeniului de definiție lim x → π 2 + π · k + 0 tg (x) = - ∞ , lim x → π 2 + π · k - 0 tg (x) = + ∞ . Astfel, dreptele x = π 2 + π · k k ∈ Z sunt asimptote verticale;
• funcția dispare când x = π k pentru k ∈ Z (Z este mulțimea numerelor întregi);
• interval: y ∈ - ∞ ; +∞ ;
• această funcție este impară deoarece y (- x) = - y (x) ;
• funcția crește la - π 2 + π · k ; π 2 + π k , k ∈ Z ;
• funcţia tangentă este concavă pentru x ∈ [ π · k ; π 2 + π k) , k ∈ Z și convex pentru x ∈ (- π 2 + π k ; π k ] , k ∈ Z ;
• punctele de inflexiune au coordonatele π k; 0 , k ∈ Z ;

1. Funcția cotangentă: y = c t g (x)

Graficul acestei funcții se numește cotangentoid. .

Definiția 21

Proprietățile funcției cotangente:

• domeniu de definiție: x ∈ (π k ; π + π k) , unde k ∈ Z (Z este mulțimea numerelor întregi);

Comportarea funcției cotangente la limita domeniului de definiție lim x → π · k + 0 t g (x) = + ∞ , lim x → π · k - 0 t g (x) = - ∞ . Astfel, dreptele x = π k k ∈ Z sunt asimptote verticale;

• cea mai mică perioadă pozitivă: T \u003d π;
• funcția dispare când x = π 2 + π k pentru k ∈ Z (Z este mulțimea numerelor întregi);
• interval: y ∈ - ∞ ; +∞ ;
• această funcție este impară deoarece y (- x) = - y (x) ;
• funcţia este descrescătoare pentru x ∈ π · k ; π + π k , k ∈ Z ;
• funcția cotangentă este concavă pentru x ∈ (π k ; π 2 + π k ] , k ∈ Z și convexă pentru x ∈ [ - π 2 + π k ; π k) , k ∈ Z ;
• punctele de inflexiune au coordonatele π 2 + π · k ; 0 , k ∈ Z ;
• nu există asimptote oblice și orizontale.

Funcțiile trigonometrice inverse sunt arcsinus, arccosinus, arctangent și arccotangent. Adesea, datorită prezenței prefixului „arc” în nume, funcțiile trigonometrice inverse sunt numite funcții arc. .

1. Funcția arcsinus: y = a r c sin (x)

Definiția 22

Proprietățile funcției arcsinus:

• această funcție este impară deoarece y (- x) = - y (x) ;
• funcția arcsinus este concavă pentru x ∈ 0; 1 și convexitatea pentru x ∈ - 1 ; 0;
• punctele de inflexiune au coordonatele (0 ; 0) , este si zero al functiei;
• nu există asimptote.

1. Funcția arccosin: y = a r c cos (x)

Definiția 23

Proprietățile funcției arccosin:

• domeniul de definire: x ∈ - 1 ; unu ;
• interval: y ∈ 0 ; π;
• această funcție este de formă generală (nici par, nici impar);
• funcția este în scădere pe întregul domeniu de definire;
• funcţia arccosinus este concavă pentru x ∈ - 1 ; 0 și convexitatea pentru x ∈ 0 ; unu ;
• punctele de inflexiune au coordonatele 0 ; π2;
• nu există asimptote.

1. Funcția arctangentă: y = a r c t g (x)

Definiția 24

Proprietățile funcției arctangente:

• domeniu de definire: x ∈ - ∞ ; +∞ ;
• interval: y ∈ - π 2 ; π2;
• această funcție este impară deoarece y (- x) = - y (x) ;
• funcția este în creștere pe întregul domeniu de definire;
• funcția arctangentă este concavă pentru x ∈ (- ∞ ; 0 ] și convexă pentru x ∈ [ 0 ; + ∞) ;
• punctul de inflexiune are coordonatele (0; 0), este si zero al functiei;
• Asimptotele orizontale sunt drepte y = - π 2 pentru x → - ∞ și y = π 2 pentru x → + ∞ (asimptotele din figură sunt linii verzi).

1. Funcția cotangentă a arcului: y = a r c c t g (x)

Definiția 25

Proprietățile funcției arc cotangent:

• domeniu de definire: x ∈ - ∞ ; +∞ ;
• interval: y ∈ (0 ; π) ;
• această funcție este de tip general;
• funcția este în scădere pe întregul domeniu de definire;
• funcţia arc cotangentă este concavă pentru x ∈ [ 0 ; + ∞) și convexitatea pentru x ∈ (- ∞ ; 0 ] ;
• punctul de inflexiune are coordonatele 0 ; π2;
• Asimptotele orizontale sunt drepte y = π la x → - ∞ (linia verde în desen) și y = 0 la x → + ∞.

Dacă observați o greșeală în text, vă rugăm să o evidențiați și să apăsați Ctrl+Enter

Funcția de putere. Aceasta este funcția: y = ax n, Unde un- permanentă. La n= 1 obținem proporționalitate directă: y = topor; la n = 2 - parabolă pătrată ; la n = - 1 - proporționalitate inversă sau hiperbolă. Astfel, aceste funcții sunt cazuri speciale ale unei funcții de putere. Știm că puterea zero a oricărui număr diferit de zero este 1, prin urmare, la n= 0 funcția putere devine o constantă:y = A, adică e. programul ei este linie dreapta, axă paralelă X, excluzând originea (clarifica te rog, De ce ? ). Toate aceste cazuri (cu A= 1 ) prezentat în Fig.13 (n 0) și Fig.14 ( n < 0). Отрицательные значения Xnu sunt luate în considerare aici ca atunci cateva functii:

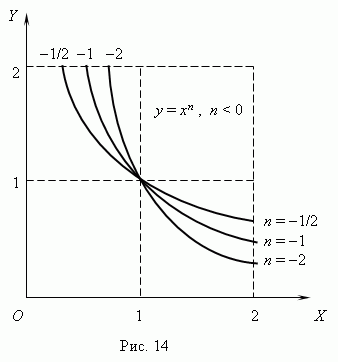
Dacă n– funcțiile întregi, de putere au sens chiar și atunci cândX< 0, но их графики имеют различный вид в зависимости от того, является ли nun număr par sau un număr impar. Figura 15 prezintă două astfel de funcții de putere: pentru n= 2 și n = 3.


La n= 2 funcția este pară șigraficul său este simetric despre axa Y. La n= 3 funcția este impară și graficul ei este simetric față de origine coordonatele. Funcţiey = X 3 numit parabolă cubică.

Figura 16 prezintă funcția . Acest functia este parabola inversă pătrată y = X 2 , graficul său se obține prin rotirea graficului parabolă pătratăîn jurul bisectoarei primului unghi de coordonate. Aceasta este o modalitate de a obține un grafic pentru oricare funcție inversă din graficul funcției sale originale. Putem vedea din grafic că aceasta este o funcție cu două valori (aceasta este indicată și de semnul ± în fața lui rădăcină pătrată). Astfel de funcții nu sunt studiate în matematica elementară, prin urmare, ca funcție, considerăm de obicei una dintre ramurile sale: superioară sau inferioară.

Mai întâi, încercați să găsiți domeniul de aplicare al funcției:

Ai reușit? Să comparăm răspunsurile:

In regula? Bine făcut!

Acum să încercăm să găsim intervalul funcției:

Găsite? Comparaţie:

A fost de acord? Bine făcut!

Să lucrăm din nou cu graficele, doar că acum este puțin mai dificil - să găsim atât domeniul funcției, cât și domeniul funcției.

Cum să găsiți atât domeniul, cât și domeniul unei funcții (avansat)

Iată ce s-a întâmplat:

Cu grafica, cred ca ti-ai dat seama. Acum să încercăm să găsim domeniul funcției în conformitate cu formulele (dacă nu știți cum să faceți acest lucru, citiți secțiunea despre):

Ai reușit? Control răspunsuri:

1. , deoarece expresia rădăcină trebuie să fie mai mare sau egală cu zero.
2. , deoarece este imposibil de împărțit la zero și expresia radicală nu poate fi negativă.
3. , întrucât, respectiv, pentru toți.
4. pentru că nu poți împărți la zero.

Cu toate acestea, mai avem încă un moment care nu a fost rezolvat...

Permiteți-mi să reiterez definiția și să mă concentrez asupra ei:

observat? Cuvântul „doar” este un element foarte, foarte important al definiției noastre. Voi încerca să vă explic pe degete.

Să presupunem că avem o funcție dată de o dreaptă. . Când, înlocuim această valoare în „regula” noastră și obținem asta. O valoare corespunde unei singure valori. Putem chiar să facem un tabel cu diferite valori și să trasăm o funcție dată pentru a verifica acest lucru.

"Uite! - spui tu, - "" se intalneste de doua ori!" Deci poate parabola nu este o funcție? Nu este!

Faptul că „” apare de două ori este departe de a fi un motiv pentru a acuza parabola de ambiguitate!

Cert este că, atunci când calculăm, avem un singur joc. Și când calculăm cu, avem un joc. Deci, așa este, parabola este o funcție. Uită-te la grafic:

Am înțeles? Dacă nu, iată un exemplu real pentru tine, departe de matematică!

Să presupunem că avem un grup de solicitanți care s-au întâlnit la depunerea documentelor, fiecare dintre ei a spus unde locuiește într-o conversație:

De acord, este destul de real că mai mulți bărbați locuiesc în același oraș, dar este imposibil ca o persoană să locuiască în mai multe orașe în același timp. Aceasta este, parcă, o reprezentare logică a „parabolei” noastre - Mai multe x-uri diferite corespund aceluiași y.

Acum să venim cu un exemplu în care dependența nu este o funcție. Să presupunem că aceiași tipi au spus pentru ce specialități au aplicat:

Aici avem o situație complet diferită: o persoană poate aplica cu ușurință pentru una sau mai multe direcții. i.e un element seturile sunt puse în corespondență elemente multiple seturi. Respectiv, nu este o functie.

Să vă testăm cunoștințele în practică.

Determinați din imagini ce este o funcție și ce nu este:

Am înțeles? Și iată răspunsuri:

• Funcția este - B,E.
• Nu este o funcție - A, B, D, D.

Te intrebi de ce? Da, iată de ce:

În toate cifrele, cu excepția ÎN)Și E) sunt mai multe pentru unul!

Sunt sigur că acum puteți distinge cu ușurință o funcție de o non-funcție, să spuneți ce este un argument și ce este o variabilă dependentă și, de asemenea, să determinați sfera argumentului și sfera funcției. Să trecem la următoarea secțiune - cum se definește o funcție?

Modalități de a seta o funcție

Ce crezi că înseamnă cuvintele "setare functie"? Așa e, înseamnă să explicăm tuturor despre ce funcție vorbim în acest caz. Mai mult, explicați în așa fel încât toată lumea să vă înțeleagă corect și graficele funcțiilor desenate de oameni conform explicației dvs. au fost aceleași.

Cum pot face acest lucru? Cum se setează o funcție? Cel mai simplu mod, care a fost deja folosit de mai multe ori în acest articol - folosind o formulă. Scriem o formulă și, substituind o valoare în ea, calculăm valoarea. Și după cum vă amintiți, o formulă este o lege, o regulă conform căreia devine clar pentru noi și pentru o altă persoană cum un X se transformă într-un Y.

De obicei, acest lucru este exact ceea ce fac ei - în sarcini vedem funcții gata făcute definite prin formule, cu toate acestea, există și alte modalități de a seta o funcție de care toată lumea uită și, prin urmare, întrebarea „cum altfel poți seta o funcție?” încurcă. Să aruncăm o privire la totul în ordine și să începem cu metoda analitică.

Mod analitic de definire a unei funcții

Metoda analitică este sarcina unei funcții care utilizează o formulă. Aceasta este cea mai universală, cuprinzătoare și lipsită de ambiguitate. Dacă aveți o formulă, atunci știți absolut totul despre funcție - puteți face un tabel de valori pe ea, puteți construi un grafic, puteți determina unde crește funcția și unde scade, în general, explorați-o în întregime.

Să luăm în considerare o funcție. Ce conteaza?

"Ce înseamnă?" - tu intrebi. Voi explica acum.

Permiteți-mi să vă reamintesc că în notație, expresia dintre paranteze se numește argument. Și acest argument poate fi orice expresie, nu neapărat simplă. În consecință, oricare ar fi argumentul (expresia între paranteze), îl vom scrie în schimb în expresie.

În exemplul nostru, va arăta astfel:

Luați în considerare o altă sarcină legată de metoda analitică de specificare a unei funcții pe care o veți avea la examen.

Găsiți valoarea expresiei, la.

Sunt sigur că la început, ți-a fost frică când ai văzut o astfel de expresie, dar nu este absolut nimic înfricoșător în ea!

Totul este la fel ca în exemplul anterior: oricare ar fi argumentul (expresia între paranteze), îl vom scrie în schimb în expresie. De exemplu, pentru o funcție.

Ce ar trebui făcut în exemplul nostru? În schimb, trebuie să scrieți și în loc de -:

scurtați expresia rezultată:

Asta e tot!

Muncă independentă

Acum încercați să găsiți singur sensul următoarelor expresii:

1. , dacă
2. , dacă

Ai reușit? Să comparăm răspunsurile noastre: Suntem obișnuiți cu faptul că funcția are forma

Chiar și în exemplele noastre, definim funcția în acest fel, dar analitic este posibil să definim funcția implicit, de exemplu.

Încercați să construiți singur această funcție.

Ai reușit?

Iată cum l-am construit.

Cu ce ​​ecuație am ajuns?

Dreapta! Liniar, ceea ce înseamnă că graficul va fi o linie dreaptă. Să facem un tabel pentru a determina ce puncte aparțin liniei noastre:

Tocmai despre asta vorbeam... Unul corespunde mai multor.

Să încercăm să desenăm ce s-a întâmplat:

Este ceea ce avem o funcție?

Așa este, nu! De ce? Încercați să răspundeți la această întrebare cu o imagine. Ce ai primit?

„Pentru că o singură valoare corespunde mai multor valori!”

Ce concluzie putem trage din asta?

Așa este, o funcție nu poate fi întotdeauna exprimată în mod explicit, iar ceea ce este „deghizat” ca funcție nu este întotdeauna o funcție!

Mod tabelar de definire a unei funcții

După cum sugerează și numele, această metodă este o placă simplă. Da Da. Ca cel pe care l-am făcut deja. De exemplu:

Aici ați observat imediat un model - Y este de trei ori mai mare decât X. Și acum sarcina „gândește foarte bine”: crezi că o funcție dată sub formă de tabel este echivalentă cu o funcție?

Să nu mai vorbim multă vreme, dar să desenăm!

Asa de. Desenăm o funcție dată în ambele moduri:

Vedeți diferența? Nu e vorba de punctele marcate! Priveste mai atent:

L-ai văzut acum? Când setăm funcția într-un mod tabelar, reflectăm pe grafic doar acele puncte pe care le avem în tabel și linia (ca și în cazul nostru) trece doar prin ele. Când definim o funcție într-un mod analitic, putem lua orice puncte, iar funcția noastră nu se limitează la ele. Iată o astfel de caracteristică. Tine minte!

Mod grafic de a construi o funcție

Mod grafic construirea unei funcții nu este mai puțin convenabilă. Ne desenăm funcția și o altă persoană interesată poate găsi cu ce este y la un anumit x și așa mai departe. Metodele grafice și analitice sunt printre cele mai comune.

Cu toate acestea, aici trebuie să vă amintiți despre ce am vorbit la început - nu fiecare „squiggle” desenat în sistemul de coordonate este o funcție! Amintit? Pentru orice eventualitate, voi copia aici definiția a ceea ce este o funcție:

De regulă, oamenii numesc de obicei exact acele trei moduri de a specifica o funcție pe care le-am analizat - analitic (folosind o formulă), tabelar și grafic, uitând complet că o funcție poate fi descrisă verbal. Asa? Da, foarte usor!

Descrierea verbală a funcției

Cum să descrii funcția verbal? Să luăm exemplul nostru recent - . Această funcție poate fi descris ca „fiecare valoare reală a lui x corespunde valorii sale triple”. Asta e tot. Nimic complicat. Desigur, veți obiecta - „există funcții atât de complexe, încât este pur și simplu imposibil de stabilit verbal!” Da, există unele, dar există funcții care sunt mai ușor de descris verbal decât de stabilit cu o formulă. De exemplu: „fiecărei valori naturale a lui x corespunde diferenței dintre cifrele din care constă, în timp ce cea mai mare cifră conținută în intrarea numărului este luată ca minuend”. Acum luați în considerare modul în care descrierea noastră verbală a funcției este implementată în practică:

Cea mai mare cifră dintr-un număr dat -, respectiv, - se reduce, apoi:

Principalele tipuri de funcții

Acum să trecem la cele mai interesante - vom lua în considerare principalele tipuri de funcții cu care ați lucrat/lucrați și veți lucra în cursul școlii și institutului de matematică, adică le vom cunoaște, ca să spunem așa, și le da descriere scurta. Citiți mai multe despre fiecare funcție în secțiunea corespunzătoare.

Funcție liniară

O funcție a formei, unde sunt numere reale.

Graficul acestei funcții este o linie dreaptă, deci construcția funcție liniară se reduce la găsirea coordonatelor a două puncte.

Poziție directă pe plan de coordonate depinde de factorul de pantă.

Domeniul de aplicare al funcției (denumit și intervalul de argumente) - .

Gama de valori este .

funcţie pătratică

Funcția formei, unde

Graficul funcției este o parabolă, când ramurile parabolei sunt îndreptate în jos, când - în sus.

Multe proprietăți funcţie pătratică depind de valoarea discriminantului. Discriminantul se calculează prin formula

Poziția parabolei pe planul de coordonate în raport cu valoarea și coeficientul este prezentată în figură:

Domeniu

Gama de valori depinde de extremul funcției date (vârful parabolei) și de coeficient (direcția ramurilor parabolei)

Proporționalitate inversă

Funcția dată de formula, unde

Numărul se numește factor de proporționalitate inversă. În funcție de ce valoare, ramurile hiperbolei sunt în pătrate diferite:

Domeniu - .

Gama de valori este .

REZUMAT ȘI FORMULA DE BAZĂ

1. O funcție este o regulă conform căreia fiecărui element al unei mulțimi i se atribuie un element unic al mulțimii.

• - aceasta este o formulă care denotă o funcție, adică dependența unei variabile de alta;
• - variabilă, sau argument;
• - valoare dependentă - se modifică atunci când argumentul se schimbă, adică după unii anumită formulă, reflectând dependența unei cantități de alta.

2. Valorile argumentelor valide, sau domeniul de aplicare al unei funcții, este ceea ce este legat de posibilul sub care funcția are sens.

3. Gama de valori ale funcției- acestea sunt valorile necesare, cu valori valide.

4. Există 4 moduri de a seta funcția:

• analitice (folosind formule);
• tabular;
• grafic
• descriere verbală.

5. Principalele tipuri de funcții:

• : , unde, sunt numere reale;
• : , Unde;
• : , Unde.

Universitatea Nationala de Cercetare

Departamentul de Geologie Aplicată

Rezumat pe matematica superioara

La subiect: „Funcții elementare de bază,

proprietățile și graficele lor"

Efectuat:

Verificat:

profesor

Definiție. Funcția dată de formula y=a x (unde a>0, a≠1) se numește funcție exponențială cu baza a.

Să formulăm principalele proprietăți ale funcției exponențiale:

1. Domeniul definiției este mulțimea (R) a tuturor numerelor reale.

2. Gama de valori este mulțimea (R+) a tuturor numerelor reale pozitive.

3. Când a > 1, funcția crește pe întreaga linie reală; la 0<а<1 функция убывает.

4. Este o funcție generală.

, pe intervalul xО [-3;3] , pe intervalul xО [-3;3]

O funcție de forma y(х)=х n , unde n este numărul ОR, se numește funcție de putere. Numărul n poate lua diferite valori: atât întreg cât și fracționar, atât par, cât și impar. În funcție de aceasta, funcția de putere va avea o formă diferită. Luați în considerare cazuri speciale care sunt funcții de putere și reflectă principalele proprietăți ale acestui tip de curbe în următoarea ordine: funcție de putere y \u003d x² (o funcție cu exponent par - o parabolă), o funcție de putere y \u003d x³ (o funcție cu un exponent impar - o parabolă cubică) și funcția y \u003d √ x (x la puterea lui ½) (funcție cu un exponent fracțional), o funcție cu un exponent întreg negativ (hiperbolă).

Funcția de putere y=x²

1. D(x)=R – funcția este definită pe toată axa numerică;

2. E(y)= și crește pe interval

Funcția de putere y=x³

1. Graficul funcției y \u003d x³ se numește parabolă cubică. Funcția de putere y=x³ are următoarele proprietăți:

2. D(x)=R – funcția este definită pe toată axa numerică;

3. E(y)=(-∞;∞) – funcția ia toate valorile din domeniul său de definiție;

4. Când x=0 y=0 – funcția trece prin originea O(0;0).

5. Funcția crește pe întregul domeniu de definiție.

6. Funcția este impară (simetrică față de origine).

, pe intervalul xн [-3;3]

În funcție de factorul numeric din fața lui x³, funcția poate fi abruptă / plată și crește / descrește.

Funcția de putere cu exponent negativ întreg:

Dacă exponentul n este impar, atunci graficul unei astfel de funcții de putere se numește hiperbolă. O funcție de putere cu un exponent întreg negativ are următoarele proprietăți:

1. D(x)=(-∞;0)U(0;∞) pentru orice n;

2. E(y)=(-∞;0)U(0;∞) dacă n este un număr impar; E(y)=(0;∞) dacă n este un număr par;

3. Funcția scade pe întregul domeniu de definiție dacă n este un număr impar; funcția crește pe intervalul (-∞;0) și scade pe intervalul (0;∞) dacă n este un număr par.

4. Funcția este impară (simetrică față de origine) dacă n este un număr impar; o funcție este par dacă n este un număr par.

5. Funcția trece prin punctele (1;1) și (-1;-1) dacă n este un număr impar și prin punctele (1;1) și (-1;1) dacă n este un număr par.

, pe intervalul xн [-3;3]

Funcția de putere cu exponent fracționar

O funcție de putere cu un exponent fracționar al formei (imagine) are un grafic al funcției prezentate în figură. O funcție de putere cu un exponent fracționar are următoarele proprietăți: (imagine)

1. D(x) ОR, dacă n este un număr impar și D(x)= , pe intervalul xО , pe intervalul xО [-3;3]

Funcția logaritmică y \u003d log a x are următoarele proprietăți:

1. Domeniul definiției D(x)н (0; + ∞).

2. Gama de valori E(y) О (- ∞; + ∞)

3. Funcția nu este nici pară, nici impară (generală).

4. Funcția crește pe intervalul (0; + ∞) pentru a > 1, scade pe (0; + ∞) pentru 0< а < 1.

Graficul funcției y = log a x poate fi obținut din graficul funcției y = a x folosind o transformare de simetrie în jurul dreptei y = x. În Figura 9, este reprezentat un grafic al funcției logaritmice pentru a > 1, iar în Figura 10 - pentru 0< a < 1.

; pe intervalul xн ; pe intervalul xО

Funcțiile y \u003d sin x, y \u003d cos x, y \u003d tg x, y \u003d ctg x sunt numite funcții trigonometrice.

Funcțiile y \u003d sin x, y \u003d tg x, y \u003d ctg x sunt impare, iar funcția y \u003d cos x este pară.

Funcția y \u003d sin (x).

1. Domeniul definiției D(x) ОR.

2. Interval de valori E(y) О [ - 1; unu].

3. Funcția este periodică; perioada principală este 2π.

4. Funcția este impară.

5. Funcția crește pe intervalele [ -π/2 + 2πn; π/2 + 2πn] și scade pe intervalele [ π/2 + 2πn; 3π/2 + 2πn], n О Z.

Graficul funcției y \u003d sin (x) este prezentat în Figura 11.