sens
Cel mai grozav
sens
Cel mai puţin
Punct maxim
Punct scăzut
Sarcinile de găsire a punctelor extreme ale funcției sunt rezolvate conform schemei standard în 3 pași.
Pasul 1. Aflați derivata unei funcții
- Memorați formulele derivate functii elementareși regulile de bază de diferențiere pentru a găsi derivata.
y′(x)=(x3−243x+19)′=3x2−243.
Pasul 2. Aflați zerourile derivatei
- Rezolvați ecuația rezultată pentru a găsi zerourile derivatei.
3x2−243=0⇔x2=81⇔x1=−9,x2=9.
Pasul 3. Găsiți puncte extreme
- Utilizați metoda spațierii pentru a determina semnele derivatei;
- În punctul minim, derivata este zero și își schimbă semnul din minus în plus, iar în punctul maxim, din plus în minus.
Să aplicăm această abordare pentru a rezolva următoarea problemă:
Aflați punctul maxim al funcției y=x3−243x+19.
1) Aflați derivata: y′(x)=(x3−243x+19)′=3x2−243;
2) Rezolvați ecuația y′(x)=0: 3x2−243=0⇔x2=81⇔x1=−9,x2=9;
3) Derivata este pozitivă pentru x>9 și x<−9 и отрицательная при −9 Cum să găsiți cea mai mare și cea mai mică valoare a unei funcții Pentru a rezolva problema găsirii celor mai mari și mai mici valori ale funcției necesar: Ajută în multe sarcini teorema: Dacă există un singur punct extremum pe segment și acesta este punctul minim, atunci cea mai mică valoare a funcției este atinsă în el. Dacă acesta este punctul maxim, atunci valoarea maximă este atinsă la el. 14. Conceptul și proprietățile de bază ale integralei nedefinite. Dacă funcţia f(X X, și k- numărul, atunci Pe scurt vorbind: constanta poate fi scoasă din semnul integral. Dacă funcţiile f(X) și g(X) au antiderivate pe interval X, apoi Pe scurt vorbind: integrala sumei este egală cu suma integralelor. Dacă funcţia f(X) are o antiderivată pe interval X, atunci pentru punctele interioare ale acestui interval: Pe scurt vorbind: derivata integralei este egală cu integrandul. Dacă funcţia f(X) este continuă pe interval Xși este diferențiabilă în punctele interioare ale acestui interval, atunci: Pe scurt vorbind: integrala diferenţialului unei funcţii este egală cu acea funcţie plus constanta de integrare. Să dăm o definiție matematică riguroasă concepte de integrală nedefinită. Expresia amabilă se numește integrală a funcției f(x)
, Unde f(x)
- funcția integrand, care este dată (cunoscută), dx
- diferential X
, cu simbol mereu prezent dx
. Definiție. Integrală nedefinită numită funcție F(x) + C
, care conține o constantă arbitrară C
, a cărui diferenţială este egală cu integrand expresie f(x)dx
, adică Amintiți-vă că - diferenţial de funcţieși se definește după cum urmează: Găsirea problemei integrală nedefinită este să găsești o funcție derivat care este egal cu integrandul. Această funcție este determinată până la o constantă, deoarece derivata constantei este zero. De exemplu, se știe că , apoi se dovedește că Găsirea sarcinii integrală nedefinită de la funcții nu este atât de simplu și ușor pe cât pare la prima vedere. În multe cazuri, trebuie să existe abilități în a lucra cu integrale nedefinite, ar trebui să fie o experiență care vine cu practică și constantă exemple de rezolvare pentru integrale nedefinite. Merită luat în considerare faptul că integrale nedefinite din unele funcții (sunt destul de multe) nu sunt luate în funcții elementare. 15. Tabelul integralelor nedefinite de bază. Formule de bază 16. Integrală definită ca limită a sumei integrale. Sensul geometric și fizic al integralei. Fie definită funcția y=ƒ(x) pe segmentul [a; grup< b. Выполним следующие действия. 1. Folosind punctele x 0 \u003d a, x 1, x 2, ..., x n \u003d B (x 0 2. În fiecare segment parțial , i = 1,2,...,n, alegem un punct arbitrar cu i є și calculăm valoarea funcției la acesta, adică valoarea ƒ(cu i). 3. Înmulțiți valoarea găsită a funcției ƒ (din i) cu lungimea ∆x i =x i -x i-1 a segmentului parțial corespunzător: ƒ (din i) ∆х i. 4. Compuneți suma S n a tuturor acestor produse: Suma formei (35.1) se numește suma integrală a funcției y \u003d ƒ (x) pe segmentul [a; b]. Notăm cu λ lungimea celui mai mare segment parțial: λ = max ∆x i (i = 1,2,..., n). 5. Aflați limita sumei integrale (35.1) ca n → ∞ astfel încât λ→0. Dacă, în plus, suma integrală S n are o limită I, care nu depinde de metoda de împărțire a segmentului [a; b] în segmente parțiale, nici din alegerea punctelor din ele, atunci numărul I se numește integrală definită a funcției y \u003d ƒ (x) pe segmentul [a; b] și se notează astfel, Numerele a și b se numesc, respectiv, limita inferioară și superioară de integrare, ƒ(x) - integrandul, ƒ(x) dx - integrandul, x - variabila de integrare, segmentul [a; b] - zona (segmentul) de integrare. Funcția y \u003d ƒ (x), pentru care pe segmentul [a; b] pe acest interval există o integrală definită numită integrabilă. Să formulăm acum teorema existenței pentru o integrală definită. Teorema 35.1 (Cauchy). Dacă funcția y = ƒ(x) este continuă pe segmentul [a; b], apoi integrala definită Rețineți că continuitatea unei funcții este o condiție suficientă pentru integrabilitatea acesteia. Cu toate acestea, o integrală definită poate exista și pentru unele funcții discontinue, în special, pentru orice funcție care este mărginită pe un interval și are un număr finit de puncte de discontinuitate pe acesta. Să subliniem câteva proprietăți ale integralei definite care decurg direct din definiția ei (35.2). 1. Integrala definită este independentă de notația variabilei de integrare: Aceasta rezultă din faptul că suma integrală (35.1) și, în consecință, limita ei (35.2) nu depind de ce literă denotă argumentul acestei funcții. 2. O integrală definită cu aceleași limite de integrare este egală cu zero: 3. Pentru orice număr real c. 17. Formula Newton-Leibniz. Proprietățile de bază ale unei integrale definite. Lasă funcția y = f(x) continuu pe segment
și F(x) este una dintre antiderivatele funcției de pe acest segment, atunci formula Newton-Leibniz: Se numește formula Newton-Leibniz formula de bază a calculului integral. Pentru a demonstra formula Newton-Leibniz, avem nevoie de conceptul de integrală cu limită superioară variabilă. Dacă funcţia y = f(x) continuu pe segment
, atunci integrala formei pentru argument este o funcție a limitei superioare. Notăm această funcție Într-adevăr, să scriem incrementul funcției corespunzătoare incrementului argumentului și să folosim a cincea proprietate a integralei definite și corolarul din a zecea proprietate: Să rescriem această egalitate în formă Calcula Fa), folosind prima proprietate a integralei definite: Incrementul unei funcții este de obicei notat ca Pentru a aplica formula Newton-Leibniz, este suficient să cunoaștem unul dintre antiderivate y=F(x) integrand y=f(x) pe segment
și calculați incrementul acestei antiderivate pe acest segment. În articol, metodele de integrare sunt analizate principalele modalități de găsire a antiderivatei. Să dăm câteva exemple de calcul a integralelor definite folosind formula Newton-Leibniz pentru clarificare. Exemplu. Calculați valoarea integralei definite folosind formula Newton-Leibniz. Decizie. În primul rând, rețineți că integrandul este continuu pe interval
, prin urmare, este integrabil pe ea. (Am vorbit despre funcțiile integrabile în secțiunea privind funcțiile pentru care există o integrală definită). Din tabelul de integrale nedefinite se poate observa că, pentru o funcție, mulțimea de antiderivate pentru toate valorile reale ale argumentului (și, prin urmare, pentru ) se scrie ca . Să luăm primitivul C=0: . Acum rămâne să folosiți formula Newton-Leibniz pentru a calcula integrala definită: 18. Aplicații geometrice ale unei integrale definite. APLICAȚII GEOMETRICE ALE UNUI INTEGRAL DEFINIT Calculul volumului corporal Calculul volumului corpului din zone cunoscute ale secțiunilor paralele: Volumul corpului de rotație: ; . Exemplul 1. Aflați aria unei figuri delimitate de o curbă y=sinx, linii drepte Decizie: Găsirea ariei figurii: Exemplul 2. Calculați aria unei figuri delimitate de linii Decizie: Să găsim abscisele punctelor de intersecție ale graficelor acestor funcții. Pentru a face acest lucru, rezolvăm sistemul de ecuații De aici găsim x 1 \u003d 0, x 2 \u003d 2,5. 19. Conceptul de controale diferențiale. Ecuații diferențiale de ordinul întâi. Ecuație diferențială- o ecuație care conectează valoarea derivatei unei funcții cu funcția în sine, valorile variabilei independente, numerele (parametrii). Ordinea derivatelor incluse în ecuație poate fi diferită (formal, nu este limitată de nimic). Derivatele, funcțiile, variabilele independente și parametrii pot fi incluse în ecuație în diferite combinații, sau toate, cu excepția cel puțin una, derivate pot fi absente cu totul. Nicio ecuație care conține derivate ale unei funcții necunoscute nu este o ecuație diferențială. De exemplu, Ecuații cu diferențe parțiale(URCHP) sunt ecuații care conțin funcții necunoscute ale mai multor variabile și derivatele lor parțiale. Forma generală a unor astfel de ecuații poate fi reprezentată ca: unde sunt variabile independente și este o funcție a acestor variabile. Ordinea ecuațiilor diferențiale parțiale poate fi determinată în același mod ca și pentru ecuațiile diferențiale obișnuite. O altă clasificare importantă a ecuațiilor cu diferențe parțiale este împărțirea lor în ecuații de tipuri eliptice, parabolice și hiperbolice, în special pentru ecuațiile de ordinul doi. Atât ecuațiile diferențiale obișnuite, cât și ecuațiile diferențiale parțiale pot fi împărțite în liniarși neliniară. O ecuație diferențială este liniară dacă funcția necunoscută și derivatele ei intră în ecuație doar la prima putere (și nu se înmulțesc între ele). Pentru astfel de ecuații, soluțiile formează un subspațiu afín al spațiului funcțiilor. Teoria ecuațiilor diferențiale liniare a fost dezvoltată mult mai profund decât teoria ecuațiilor neliniare. Forma generală a unei ecuații diferențiale liniare n-a comanda: Unde pi(X) sunt funcții cunoscute ale variabilei independente, numite coeficienți ai ecuației. Funcţie r(X) din partea dreaptă se numește membru liber(singurul termen care nu depinde de funcția necunoscută) O clasă particulară importantă de ecuații liniare sunt ecuațiile diferențiale liniare cu coeficienți constanți. O subclasă de ecuații liniare sunt omogen ecuații diferențiale - ecuații care nu conțin un termen liber: r(X) = 0. Pentru ecuațiile diferențiale omogene, principiul suprapunerii este valabil: o combinație liniară de soluții particulare ale unei astfel de ecuații va fi, de asemenea, soluția acesteia. Toate celelalte ecuații diferențiale liniare sunt numite eterogen ecuatii diferentiale. Ecuațiile diferențiale neliniare în cazul general nu au metode de rezolvare dezvoltate, cu excepția unor clase particulare. În unele cazuri (cu utilizarea anumitor aproximări) acestea pot fi reduse la unele liniare. De exemplu, ecuația liniară a unui oscilator armonic · este o ecuație diferențială omogenă de ordinul doi cu coeficienți constanți. Soluția este o familie de funcții , unde și sunt constante arbitrare, care pentru o soluție specifică sunt determinate din condiții inițiale specificate separat. Această ecuație, în special, descrie mișcarea unui oscilator armonic cu o frecvență ciclică de 3. · A doua lege a lui Newton poate fi scrisă sub forma unei ecuații diferențiale · Ecuația diferențială Bessel este o ecuație omogenă liniară obișnuită de ordinul doi cu coeficienți variabili: Soluțiile sale sunt funcțiile Bessel. Un exemplu de ecuație diferențială ordinară neomogenă neliniară de ordinul I: În următorul grup de exemple, funcția necunoscută u depinde de două variabile Xși t sau Xși y. Ecuație diferențială parțială liniară omogenă de ordinul întâi: Ecuație de undă unidimensională - o ecuație liniară omogenă în derivate parțiale de tip hiperbolic de ordinul doi cu coeficienți constanți, descrie vibrația șirului, dacă - abaterea șirului într-un punct cu coordonate X la momentul t, și parametrul A setează proprietățile șirului: Ecuația Laplace în spațiul bidimensional este o ecuație diferențială parțială omogenă liniară de ordinul doi de tip eliptică cu coeficienți constanți, care apare în multe probleme fizice de mecanică, conducție termică, electrostatică, hidraulică: Ecuația Korteweg-de Vries, o ecuație diferențială parțială neliniară de ordinul trei care descrie unde neliniare staționare, inclusiv solini: 20. Ecuații diferențiale cu separabil aplicabil. Ecuații liniare și metoda Bernoulli. O ecuație diferențială liniară de ordinul întâi este o ecuație liniară în raport cu o funcție necunoscută și derivata ei. Are forma unui grad întreg. Într-adevăr, dacă găsim și substituim în ecuațiile tipurilor considerate, obținem egalitatea corectă. După cum se menționează în articolul despre ecuații omogene, dacă prin condiție se cere să se găsească doar o anumită soluție, atunci funcția, din motive evidente, nu ne deranjează, dar când se cere să se găsească o soluție generală / integrală, atunci este necesar să ne asigurăm că această funcție este nu pierdut! Am adus toate soiurile populare ale ecuației Bernoulli într-o pungă mare cu cadouri și am procedat la distribuire. Atârnă-ți șosetele sub copac. Exemplul 1 Găsiți o soluție particulară a ecuației diferențiale corespunzătoare condiției inițiale date. Probabil, mulți au fost surprinși că primul cadou a fost imediat scos din geantă împreună cu Problema Cauchy. Acesta nu este un accident. Când se propune o ecuație Bernoulli pentru o soluție, din anumite motive este adesea necesar să se găsească o anumită soluție. În colecția mea, am efectuat un eșantion aleatoriu din 10 ecuații Bernoulli, iar soluția generală (fără o soluție specială) trebuie găsită în doar 2 ecuații. Dar, de fapt, acesta este un fleac, deoarece soluția generală va trebui căutată în orice caz. Decizie: Acest diffur are forma și, prin urmare, este ecuația Bernoulli Cea mai mare valoare a funcției Cea mai mică valoare a funcției După cum a spus nașul: „Nimic personal”. Numai derivate! Sarcina 12 din statistici este considerată destul de dificilă și totul pentru că băieții nu au citit acest articol (glumă). În cele mai multe cazuri, nepăsarea este de vină. Sarcina 12 este de două tipuri: Sarcini cu examen: Găsiți punctul maxim al funcției Găsiți punctul minim al funcției Sarcini cu examen: Aflați cea mai mare valoare a funcției pe intervalul [−4; −1] Răspuns: -6 Găsiți cea mai mare valoare a funcției de pe segment Raspuns: 11 Constatari: Punctul extremum al unei funcții este punctul din domeniul funcției în care valoarea funcției ia o valoare minimă sau maximă. Valorile funcției din aceste puncte sunt numite extreme (minime și maxime) ale funcției. Definiție. Punct X1
domeniul de aplicare al funcției f(X) se numește punctul maxim al funcției
, dacă valoarea funcției în acest punct este mai mare decât valorile funcției în puncte suficient de apropiate de ea, situate la dreapta și la stânga acesteia (adică inegalitatea f(X0
) > f(X 0
+ Δ X)
X1
maxim. Definiție. Punct X2
domeniul de aplicare al funcției f(X) se numește punctul minim al funcției, dacă valoarea funcției în acest punct este mai mică decât valorile funcției în puncte suficient de apropiate de ea, situate la dreapta și la stânga acesteia (adică inegalitatea f(X0
) < f(X 0
+ Δ X)
). În acest caz, se spune că funcția are la punctul X2
minim. Să spunem ideea X1
- punctul maxim al functiei f(X). Apoi în intervalul până la X1
funcția crește, deci derivata funcției este mai mare decât zero ( f "(X) > 0 ), iar în intervalul de după X1
funcția este în scădere, deci derivată de funcție mai putin de zero ( f "(X) < 0
).
Тогда в точке X1
Să presupunem, de asemenea, că ideea X2
- punctul minim al functiei f(X). Apoi în intervalul până la X2
funcția este descrescătoare și derivata funcției este mai mică decât zero ( f "(X) < 0
), а в интервале
после X2
funcția este în creștere și derivata funcției este mai mare decât zero ( f "(X) > 0). În acest caz și la punct X2
derivata functiei este zero sau nu exista. teorema lui Fermat ( semn necesar existența unui extremum al funcției). Dacă punct X0
- punctul extremum al funcției f(X), atunci în acest moment derivata funcției este egală cu zero ( f "(X) = 0 ) sau nu există. Definiție. Sunt numite punctele în care derivata unei funcții este egală cu zero sau nu există puncte critice
. Exemplul 1 Să luăm în considerare o funcție. La punctul X= 0 derivata functiei este egala cu zero, deci punctul X= 0 este punctul critic. Cu toate acestea, după cum se poate observa pe graficul funcției, aceasta crește în întregul domeniu de definiție, deci punctul X= 0 nu este un punct extrem al acestei funcții. Astfel, condițiile ca derivata unei funcții într-un punct să fie egală cu zero sau să nu existe sunt condiții necesare pentru un extremum, dar nu suficiente, deoarece pot fi date și alte exemple de funcții pentru care aceste condiții sunt îndeplinite, dar funcția nu are un extremum în punctul corespunzător. Asa de trebuie să aibă suficiente indicații, permițând să se judece dacă există un extremum într-un anumit punct critic și care dintre ele - un maxim sau un minim. Teoremă (primul criteriu suficient pentru existența unui extremum al unei funcții). Punct critic X0
f(X) , dacă derivata funcției își schimbă semnul la trecerea prin acest punct, iar dacă semnul se schimbă din „plus” în „minus”, atunci punctul maxim, iar dacă din „minus” în „plus”, atunci punctul minim . Dacă aproape de punct X0
, la stânga și la dreapta acesteia, derivata își păstrează semnul, asta înseamnă că funcția fie scade, fie crește doar într-o vecinătate a punctului X0
. În acest caz, la punctul X0
nu există extremum. Asa de, pentru a determina punctele extreme ale funcției, trebuie să faceți următoarele
: Exemplul 2 Găsiți extremele unei funcții Decizie. Să găsim derivata funcției: Echivalează derivata cu zero pentru a găsi punctele critice: Deoarece pentru orice valoare a lui „x” numitorul nu este egal cu zero, atunci echivalăm numărătorul cu zero: Am un punct critic X= 3 . Determinăm semnul derivatei în intervalele delimitate de acest punct: în intervalul de la minus infinit la 3 - semnul minus, adică funcția scade, în intervalul de la 3 la plus infinit - un semn plus, adică funcția crește. Adică punct X= 3 este punctul minim. Găsiți valoarea funcției în punctul minim: Astfel, punctul extremum al funcției se găsește: (3; 0) , și este punctul minim. Teoremă (al doilea criteriu suficient pentru existența unui extremum al unei funcții). Punct critic X0
este punctul extremum al funcției f(X), dacă derivata a doua a funcției în acest punct nu este egală cu zero ( f ""(X) ≠ 0 ), în plus, dacă derivata a doua este mai mare decât zero ( f ""(X) > 0 ), atunci punctul maxim și dacă derivata a doua este mai mică decât zero ( f ""(X) < 0
),
то точкой минимума. Observaţie 1. Dacă la un punct X0
atât prima cât și a doua derivată dispar, apoi în acest moment este imposibil să judecăm prezența unui extremum pe baza celui de-al doilea semn suficient. În acest caz, trebuie să utilizați primul criteriu suficient pentru extremul funcției. Observația 2. Al doilea criteriu suficient pentru extremul unei funcții este de asemenea inaplicabil atunci când derivata întâi nu există în punctul staționar (atunci nici derivata a doua nu există). În acest caz, este necesar să se folosească și primul criteriu suficient pentru extremul funcției. Din definițiile de mai sus rezultă că extremul unei funcții este de natură locală - aceasta este cea mai mare și cea mai mică valoare a funcției în comparație cu cele mai apropiate valori. Să presupunem că luați în considerare câștigurile dvs. într-un interval de timp de un an. Dacă în mai ați câștigat 45.000 de ruble, iar în aprilie 42.000 de ruble și în iunie 39.000 de ruble, atunci câștigurile din mai sunt maximul funcției de câștig în comparație cu cele mai apropiate valori. Dar în octombrie ai câștigat 71.000 de ruble, în septembrie 75.000 de ruble și în noiembrie 74.000 de ruble, deci câștigurile din octombrie sunt minimul funcției de câștig în comparație cu valorile din apropiere. Și puteți observa cu ușurință că maximul dintre valorile lunilor aprilie-mai-iunie este mai mic decât cel minim din septembrie-octombrie-noiembrie. În general, o funcție poate avea mai multe extreme pe un interval și se poate dovedi că orice minim al funcției este mai mare decât orice maxim. Deci, pentru funcția prezentată în figura de mai sus, . Adică, nu trebuie să credem că maximul și minimul funcției sunt, respectiv, valorile maxime și minime ale acesteia pe întregul segment luat în considerare. În punctul maxim, funcția are cea mai mare valoare numai în comparație cu acele valori pe care le are în toate punctele suficient de aproape de punctul maxim, iar în punctul minim, valoarea cea mai mică numai în comparație cu acele valori care are în toate punctele suficient de aproape de punctul minim. Prin urmare, putem rafina conceptul de puncte extreme ale unei funcții prezentate mai sus și numim punctele minime puncte minime locale, iar punctele maxime - puncte maxime locale. Exemplul 3 Rezolvare.Funcția este definită și continuă pe întreaga dreaptă numerică. Derivatul său Pentru interval, punctul de referință poate fi : găsim . Luând un punct în interval, obținem , iar luând un punct în interval, avem . Deci, în intervalele și , și în intervalul . Conform primei semn suficient extremum, nu există extremum în punct (deoarece derivata își păstrează semnul în intervalul ), iar în punct funcția are un minim (deoarece derivata își schimbă semnul din minus în plus când trece prin acest punct). Găsiți valorile corespunzătoare ale funcției: , și . În interval, funcția scade, deoarece în acest interval , iar în interval crește, deoarece în acest interval. Pentru a clarifica construcția graficului, găsim punctele de intersecție ale acestuia cu axele de coordonate. Când obținem o ecuație ale cărei rădăcini și , adică două puncte (0; 0) și (4; 0) ale graficului funcției se găsesc. Folosind toate informațiile primite, construim un grafic (vezi la începutul exemplului). Pentru autoverificare în timpul calculelor, puteți utiliza calculator de derivate online . Exemplul 4 Găsiți extremele funcției și construiți graficul acesteia. Domeniul funcției este întreaga dreaptă numerică, cu excepția punctului, adică. . Pentru a scurta studiul, putem folosi faptul că această funcție este pară, deoarece Găsirea derivatei 1) 2) dar funcția suferă o întrerupere în acest punct, deci nu poate fi un punct extremum. Prin urmare, funcţie dată are două puncte critice: și . Ținând cont de paritatea funcției, verificăm doar punctul după al doilea semn suficient al extremului. Pentru a face acest lucru, găsim derivata a doua Pentru a obține o imagine mai completă a graficului funcției, să aflăm comportamentul acesteia la limitele domeniului de definiție: (aici simbolul indică dorința X la zero în dreapta și X rămâne pozitiv; în mod similar înseamnă aspirație X la zero în stânga și X rămâne negativ). Astfel, dacă , atunci . În continuare, găsim acestea. daca atunci . Graficul funcției nu are puncte de intersecție cu axele. Poza este la începutul exemplului. Pentru autoverificare în timpul calculelor, puteți utiliza calculator de derivate online . Exemplul 8 Aflați extremele funcției. Decizie. Găsiți domeniul funcției. Deoarece inegalitatea trebuie să se mențină, obținem din . Să găsim prima derivată a funcției. Teorema.
(condiție necesară pentru existența unui extremum) Dacă funcția f (x) este diferențiabilă în punctul x \u003d x 1 și punctul x 1 este un punct extrem, atunci derivata funcției dispare în acest punct. Dovada.
Să presupunem că funcția f(x) are un maxim în punctul x = x 1. Atunci, pentru Dх>0 pozitiv suficient de mic, următoarea inegalitate este adevărată: Prioritate A: Acestea. dacă Dх®0, dar Dх<0, то f¢(x 1) ³ 0, а если Dх®0, но Dх>0, apoi f¢(x 1) £ 0. Și acest lucru este posibil numai dacă la Dх®0 f¢(x 1) = 0. Pentru cazul în care funcția f(x) are un minim în punctul x 2, teorema se demonstrează în mod similar. Teorema a fost demonstrată. Consecinţă.
Reversul nu este adevărat. Dacă derivata unei funcții la un moment dat este egală cu zero, atunci aceasta nu înseamnă că funcția are un extremum în acest punct. Un exemplu elocvent în acest sens este funcția y \u003d x 3, a cărei derivată în punctul x \u003d 0 este egală cu zero, dar în acest moment funcția are doar o inflexiune și nu un maxim sau un minim. Definiție. puncte critice Funcțiile sunt puncte în care derivata funcției nu există sau este egală cu zero. Teorema considerată mai sus ne oferă condițiile necesare pentru existența unui extremum, dar acest lucru nu este suficient. Exemplu: f(x) = ôxô Exemplu: f(x) = În punctul x = 0 funcția are un minim, dar în punctul x = 0 funcția nu are niciunul nu are derivat. maxim, fără minim, nu În general, funcția f(x) poate avea un extrem în punctele în care derivata nu există sau este egală cu zero. Teorema.
(Condiții suficiente existența unui extremum) Fie ca funcția f(x) să fie continuă în intervalul (a, b), care conține punctul critic x 1 și să fie diferențiabilă în toate punctele acestui interval (cu excepția, poate, a punctului x 1 însuși). Dacă, la trecerea prin punctul x 1 de la stânga la dreapta, derivata funcției f¢(x) își schimbă semnul din „+” în „-“, atunci în punctul x = x 1 funcția f(x) are un maxim, iar dacă derivata își schimbă semnul de la „- „ la „+” - atunci funcția are un minim. Dovada.
Lasa Conform teoremei lui Lagrange: f(x) - f(x 1) = f¢(e)(x - x 1), unde x< e < x 1 . Atunci: 1) Dacă x< x 1 , то e < x 1 ; f¢(e)>0; f¢(e)(x – x 1)<0, следовательно f(x) – f(x 1)<0 или f(x) < f(x 1). 2) Dacă x > x 1, atunci e > x 1 f¢(e)<0; f¢(e)(x – x 1)<0, следовательно f(x) – f(x 1)<0 или f(x) < f(x 1). Deoarece răspunsurile sunt aceleași, putem spune că f(x)< f(x 1) в любых точках вблизи х 1 , т.е. х 1 – точка максимума. Dovada teoremei pentru punctul minim este similară. Teorema a fost demonstrată. Pe baza celor de mai sus, este posibil să se dezvolte o singură procedură pentru găsirea celor mai mari și cea mai mică valoare functii pe segment: 1) Aflați punctele critice ale funcției. 2) Găsiți valorile funcției în punctele critice. 3) Găsiți valorile funcției la capetele segmentului. 4) Alegeți dintre valorile obținute cea mai mare și cea mai mică. Investigarea unei funcții la un extrem folosind derivate de ordin superior. Fie f¢(x 1) = 0 în punctul x = x 1 și fie f¢¢(x 1) să existe și să fie continuă într-o vecinătate a punctului x 1 . Teorema.
Dacă f¢(x 1) = 0, atunci funcția f(x) în punctul x = x 1 are un maxim dacă f¢¢(x 1)<0 и минимум, если f¢¢(x 1)>0.
Dovada.
Fie f¢(x 1) = 0 și f¢¢(x 1)<0. Т.к. функция f(x) непрерывна, то f¢¢(x 1) будет отрицательной и в некоторой малой окрестности точки х 1 . pentru că f¢¢(x) = (f¢(x))¢< 0, то f¢(x) убывает на отрезке, содержащем точку х 1 , но f¢(x 1)=0, т.е. f¢(x) >0 la x Pentru cazul unei funcții minime, teorema se demonstrează în mod similar. Dacă f¢¢(x) = 0, atunci natura punctului critic este necunoscută. Sunt necesare cercetări suplimentare pentru a-l determina. Convexitatea și concavitatea unei curbe. Puncte de inflexiune. Definiție.
Curba este convexă sus pe intervalul (a, b) dacă toate punctele sale se află sub oricare dintre tangentele sale pe acest interval. O curbă cu un punct convex în sus se numește convex, iar curba convexă în jos se numește concav. Figura prezintă o ilustrare a definiției de mai sus. Teorema 1.
Dacă în toate punctele intervalului (a, b) derivata a doua a funcției f(x) este negativă, atunci curba y = f(x) este convexă în sus (convexă). Dovada.
Fie x 0 О (a, b). Desenați o tangentă la curbă în acest punct. Ecuația curbei: y = f(x); Ecuația tangentei: Trebuie demonstrat că . Conform teoremei Lagrange pentru f(x) – f(x 0): , x 0< c < x. Conform teoremei Lagrange pentru Fie x > x 0 apoi x 0< c 1 < c < x. Т.к. x – x 0 >0 și c - x 0 > 0 și, în plus, prin condiție Prin urmare, . Fie x< x 0 тогда x < c < c 1 < x 0 и x – x 0 < 0, c – x 0 < 0, т.к. по условию то Se poate demonstra în mod similar că dacă f¢¢(x) > 0 pe intervalul (a, b), atunci curba y=f(x) este concavă pe intervalul (a, b). Teorema a fost demonstrată. Definiție.
Se numește punctul care separă partea convexă a curbei de partea concavă punct de inflexiune. Evident, în punctul de inflexiune, tangenta intersectează curba. Teorema 2.
Fie curba definită de ecuația y = f(x). Dacă derivata a doua f¢¢(a) = 0 sau f¢¢(a) nu există și la trecerea prin punctul x = a f¢¢(x) își schimbă semnul, atunci punctul curbei cu abscisa x = a este un punct de inflexiune. Dovada.
1) Fie f¢¢(x)< 0 при х < a и f¢¢(x) >0 pentru x > a. Apoi la X< a кривая выпукла, а при x >o curbă este concavă, adică punctul x = a este punctul de inflexiune. 2) Fie f¢¢(x) > 0 pentru x< b и f¢¢(x) < 0 при x < b. Тогда при x < b кривая обращена выпуклостью вниз, а при x >b - se umflă. Atunci x = b este un punct de inflexiune. Teorema a fost demonstrată. Asimptote. În studiul funcțiilor, se întâmplă adesea ca atunci când coordonata x a unui punct al unei curbe este îndepărtată la infinit, curba se apropie de o anumită linie dreaptă la infinit. Definiție.
Apelat direct asimptotă curbă, dacă distanța de la punctul variabil al curbei la această linie dreaptă tinde spre zero atunci când punctul este îndepărtat la infinit. Trebuie remarcat faptul că nu orice curbă are o asimptotă. Asimptotele pot fi drepte sau oblice. Studiul funcţiilor pentru prezenţa asimptotelor are mare importanțăși vă permite să determinați mai precis natura funcției și comportamentul graficului curbei. În general, curba, apropiindu-se de asimptota ei la nesfârșit, o poate intersecta și ea, și nu la un moment dat, așa cum se arată în graficul funcției de mai jos Să luăm în considerare mai detaliat metodele de găsire a asimptotelor curbelor. Asimptote verticale. Din definiția asimptotei rezultă că dacă sau sau , atunci linia x = a este asimptota curbei y = f(x). De exemplu, pentru o funcție, linia x = 5 este asimptota verticală. Asimptote oblice. Să presupunem că curba y = f(x) are o asimptotă oblică y = kx + b. Să notăm punctul de intersecție al curbei și perpendiculara pe asimptotă - M, P - punctul de intersecție al acestei perpendiculare cu asimptota. Unghiul dintre asimptotă și axa x va fi notat cu j. Perpendiculara MQ pe axa x intersectează asimptota în punctul N. Atunci MQ = y este ordonata punctului curbei, NQ = este ordonata punctului N de pe asimptotă. După condiție: , РNMP = j, . Atunci unghiul j este constant și nu este egal cu 90 0 Apoi Deci, linia y = kx + b este o asimptotă a curbei. Pentru definiție exactă pe această linie, este necesar să se găsească o modalitate de a calcula coeficienții k și b. În expresia rezultată, scoatem x din paranteze: pentru că x®¥, atunci Apoi pentru că Rețineți că asimptotele orizontale sunt un caz special de asimptote oblice pentru k =0. Exemplu. 1) Asimptote verticale: y®+¥ x®0-0: y®-¥ x®0+0, prin urmare x = 0 este o asimptotă verticală. 2) Asimptote oblice: Astfel, linia dreaptă y = x + 2 este o asimptotă oblică. Să diagramăm funcția: Exemplu. Găsiți asimptote și reprezentați grafic funcția. Liniile x=3 și x=-3 sunt asimptotele verticale ale curbei. Găsiți asimptote oblice: y = 0 este asimptota orizontală. Exemplu. Găsiți asimptote și reprezentați grafic funcția Linia x = -2 este asimptota verticală a curbei. Să găsim asimptote oblice. În total, linia y = x - 4 este o asimptotă oblică. Schema de studiu a funcției Procesul de cercetare a unei funcții constă din mai multe etape. Pentru cea mai completă idee despre comportamentul funcției și natura graficului acesteia, este necesar să găsiți: 1) Domeniul de aplicare al funcției. Acest concept include atât domeniul valorilor, cât și domeniul unei funcții. 2) Puncte de întrerupere. (Dacă sunt disponibile). 3) Intervale de crestere si scadere. 4) Puncte de maxim și minim. 5) Maxim și valoarea minima funcţionează pe domeniul său. 6) Zone de convexitate și concavitate. 7) Puncte de inflexiune (dacă există). 8) Asimptote (dacă există). 9) Construirea unui grafic. Să folosim această schemă cu un exemplu. Exemplu. Investigați funcția și trasați graficul acesteia. Găsim zona de existență a funcției. Este evident că domeniul definirii funcția este aria (-¥; -1) È (-1; 1) È (1; ¥). La rândul său, se poate observa că liniile x = 1, x = -1 sunt asimptote verticale strâmb. Zona valoric al acestei funcții este intervalul (-¥; ¥). puncte de pauză funcțiile sunt punctele x=1, x=-1. Găsim puncte critice. Să găsim derivata funcției Puncte critice: x = 0; x = - ; x = ; x = -1; x = 1. Să găsim derivata a doua a funcției Să determinăm convexitatea și concavitatea curbei la intervale. -¥ < x < - , y¢¢ < 0, кривая выпуклая - < x < -1, y¢¢ < 0, кривая выпуклая 1 < x < 0, y¢¢ >0, curbă concavă 0 < x < 1, y¢¢ < 0, кривая выпуклая 1 < x < , y¢¢ >0, curbă concavă < x < ¥, y¢¢ >0, curbă concavă Găsirea lacune crescândși Descendentă funcții. Pentru a face acest lucru, determinăm semnele derivatei funcției pe intervale. -¥ < x < - , y¢ >0, funcția este în creștere - < x < -1, y¢ < 0, функция убывает 1 < x < 0, y¢ < 0, функция убывает 0 < x < 1, y¢ < 0, функция убывает 1 < x < , y¢ < 0, функция убывает < x < ¥, y¢¢ >0, funcția este în creștere Se poate observa că punctul x = - este un punct maxim, iar punctul x = este punctul minim. Valorile funcției în aceste puncte sunt -3/2 și, respectiv, 3/2. Despre verticală asimptote s-a spus deja mai sus. Acum să găsim asimptote oblice. Deci, ecuația asimptotă oblică este y = x. Să construim programa caracteristici: Funcțiile mai multor variabile
Când luăm în considerare funcțiile mai multor variabile, ne limităm la o descriere detaliată a funcțiilor a două variabile, deoarece toate rezultatele obtinute vor fi valabile pentru functii număr arbitrar variabile. Definiție: Dacă fiecărei perechi de numere independente (x, y) dintr-o anumită mulțime, după o anumită regulă, i se atribuie una sau mai multe valori ale variabilei z, atunci variabilei z se numește funcție a două variabile. Definiție:
Dacă o pereche de numere (x, y) corespunde unei valori a lui z, atunci funcția este numită lipsit de ambiguitate, iar dacă mai mult de unul, atunci - ambiguu. Definiție: Domeniul de aplicare al definiției funcția z este mulțimea de perechi (x, y) pentru care există funcția z. Definiție: Punct de vecinătate M 0 (x 0, y 0) cu raza r este colecția tuturor punctelor (x, y) care îndeplinesc condiția Definiție:
Se numește numărul A limită funcția f(x, y) deoarece punctul M(x, y) tinde către punctul M 0 (x 0, y 0), dacă pentru fiecare număr e > 0 există un astfel de număr r > 0 încât pentru orice punct M (x, y) pentru care condiția conditia este si ea adevarata Scrie: Definiție:
Fie punctul M 0 (x 0, y 0) să aparțină domeniului funcției f(x, y). Atunci se numește funcția z = f(x, y). continuuîn punctul M 0 (x 0, y 0), dacă în plus, punctul M(x, y) tinde spre punctul M 0 (x 0, y 0) într-un mod arbitrar. Dacă condiția (1) nu este îndeplinită în niciun moment, atunci acest punct este numit punctul limita funcțiile f(x, y). Acest lucru poate fi în următoarele cazuri: 1) Funcția z \u003d f (x, y) nu este definită în punctul M 0 (x 0, y 0). 2) Nu există limită. 3) Această limită există, dar nu este egală cu f(x 0 , y 0). Proprietate.
Dacă funcția f(x, y, …) este definită și continuă într-un și închis zona delimitata D, atunci in aceasta zona exista cel putin un punct N(x 0 , y 0 , …) astfel încât inegalitatea f(x 0 , y 0 , …) ³ f(x, y, …) precum și un punct N 1 (x 01 , y 01 , ...), astfel încât pentru toate celelalte puncte inegalitatea este adevărată f(x 01 , y 01 , …) £ f(x, y, …) atunci f(x 0 , y 0 , …) = M – cea mai mare valoare funcții și f(x 01 , y 01 , ...) = m - cea mai mică valoare funcțiile f(x, y, …) în domeniul D. O funcție continuă într-un domeniu închis și mărginit D atinge cel puțin o dată valoarea sa maximă și o dată valoarea sa minimă. Proprietate.
Dacă funcția f(x, y, …) este definită și continuă într-un domeniu închis și mărginit D, iar M și m sunt cele mai mari și, respectiv, cele mai mici valori ale funcției din acest domeniu, atunci pentru orice punct m О există este un punct N 0 (x 0 , y 0 , …) astfel încât f(x 0 , y 0 , …) = m. Pur și simplu pune, funcție continuă ia în regiunea D toate valorile intermediare între M și m. O consecință a acestei proprietăți poate fi concluzia că dacă numerele M și m au semne diferite, atunci în domeniul D funcția dispare cel puțin o dată. Proprietate.
Funcția f(x, y, …), continuă într-un domeniu mărginit închis D, limitatîn această zonă, dacă există un astfel de număr K încât pentru toate punctele ariei inegalitatea este adevărată Proprietate.
Dacă o funcție f(x, y, …) este definită și continuă într-un domeniu închis și mărginit D, atunci aceasta uniform continuuîn acest domeniu, adică pentru oricine număr pozitiv e există un astfel de număr D > 0 încât pentru oricare două puncte (x 1 , y 1) și (x 2 , y 2) ale zonei situate la o distanță mai mică decât D, inegalitatea Proprietățile de mai sus sunt similare cu proprietățile funcțiilor unei variabile care sunt continue pe un interval. Consultați Proprietățile funcțiilor continue pe un interval. Derivate și diferențiale de funcții variabile multiple. Definiție.
Fie dată o funcție z = f(x, y) într-un domeniu. Luați un punct arbitrar M(x, y) și setați incrementul Dx la variabila x. Atunci cantitatea D x z = f(x + Dx, y) – f(x, y) se numește creșterea parțială a funcției în x. Poate fi scris Apoi a sunat derivat parțial funcțiile z = f(x, y) în x. Desemnare: Derivata parțială a unei funcții în raport cu y este definită în mod similar. sens geometric derivata parțială (să spunem) este tangenta pantei tangentei trasate în punctul N 0 (x 0, y 0, z 0) la secțiunea suprafeței de către planul y \u003d y 0. Creștere completă si diferential total.
plan tangent Fie N și N 0 puncte ale suprafeței date. Să trasăm o linie dreaptă NN 0 . Planul care trece prin punctul N 0 se numeste plan tangent la suprafaţă dacă unghiul dintre secanta NN 0 şi acest plan tinde spre zero când distanţa NN 0 tinde spre zero. Definiție. normal faţă de suprafaţa în punctul N 0 se numeşte dreptă care trece prin punctul N 0 perpendicular pe planul tangent la această suprafaţă. La un moment dat, suprafața are fie un singur plan tangent, fie nu îl are deloc. Dacă suprafața este dată de ecuația z \u003d f (x, y), unde f (x, y) este o funcție diferențiabilă în punctul M 0 (x 0, y 0), planul tangent în punctul N 0 (x 0, y 0, ( x 0 ,y 0)) există și are ecuația: Ecuația pentru normala la suprafață în acest punct este: sens geometric a diferenţialului total al unei funcţii de două variabile f (x, y) în punctul (x 0, y 0) este incrementul aplicatei (coordonata z) a planului tangent la suprafaţă în timpul tranziţiei de la punctul (x 0, y 0) până la punctul (x 0 + Dx, y 0 + Dy). Așa cum se vede, sens geometric al diferenţialului total al unei funcţii a două variabile este un analog spaţial al sensului geometric al diferenţialului unei funcţii a unei variabile. Exemplu. Aflați ecuațiile planului tangent și normala la suprafață în punctul M(1, 1, 1). Ecuația planului tangent: Ecuația normală: Calcule aproximative folosind diferența totală.
Diferenţialul total al funcţiei u este: Valoarea exactă a acestei expresii este 1,049275225687319176. Derivate parțiale de ordin superior. Dacă funcția f(x, y) este definită într-un domeniu D, atunci derivatele sale parțiale și vor fi, de asemenea, definite în același domeniu sau o parte a acestuia. Vom numi aceste derivate derivate parțiale de ordinul întâi. Derivatele acestor funcții vor fi derivate parțiale de ordinul doi. Continuând să diferențiem egalitățile obținute, obținem derivate parțiale de ordin superior. Se consideră funcția y = f(x), care este considerată pe intervalul (a, b). Dacă este posibil să se specifice o astfel de b-vecinătate a punctului x1 aparținând intervalului (a, b) încât pentru tot x (x1, b) să fie satisfăcută inegalitatea f(x1) > f(x), atunci y1 = f1(x1) se numește functia maxima y = f(x) vezi fig. Maximul funcției y = f(x) se notează cu max f(x). Dacă este posibil să se specifice o vecinătate de 6 a punctului x2 aparținând intervalului (a, b) astfel încât pentru tot x să aparțină lui O(x2, 6), x nu este egal cu x2, inegalitatea f(x2)< f(x)
, atunci y2= f(x2) se numește minimul funcției y-f(x) (vezi Fig.). Un exemplu de găsire a maximului, vezi următorul videoclip Minimul funcției y = f(x) se notează cu min f(x). Cu alte cuvinte, maximul sau minimul unei funcții y = f(x) numit valoarea sa, care este mai mare (mai mică) decât toate celelalte valori luate în puncte suficient de apropiate de cea dată și diferite de aceasta. Observație 1. Funcție maximă, determinat de inegalitate se numește maxim strict; Maximul nestrict este definit de inegalitatea f(x1) > = f(x2) Observația 2. au un caracter local (acestea sunt cele mai mari și mai mici valori ale funcției într-o vecinătate suficient de mică a punctului corespunzător); minimele individuale ale unei anumite funcții pot fi mai mari decât maximele aceleiași funcție Maximul și minimul unei funcții se numește extremum.
. Extreme în găsire pentru funcții de trasare latin extremum înseamnă „extrem”
sens. Valoarea argumentului x, la care se atinge extremul, se numește punctul extremum. Condiția necesară pentru un extremum este exprimată prin următoarea teoremă. Teorema. În punctul de extremum al funcției diferențiabile și derivata ei este egală cu zero. Teorema are o semnificație geometrică simplă: tangenta la graficul unei funcții diferențiabile în punctul corespunzător este paralelă cu axa x
sau 
Funcția este numită funcția antiderivată. Antiderivată a unei funcții este determinată până la o valoare constantă.
, aici este o constantă arbitrară.
.
, iar această funcție este continuă și egalitatea 
.
Unde .
. Dacă ne amintim definiția derivatei unei funcții și mergem la limita de la , atunci obținem . Adică este unul dintre antiderivatele funcției y = f(x) pe segment
. Astfel, setul tuturor antiderivatelor F(x) poate fi scris ca , unde Cu este o constantă arbitrară.
, prin urmare, . Folosim acest rezultat pentru a calcula F(b): , adică 
. Această egalitate dă formula Newton-Leibniz demonstrabilă .
. Folosind această notație, formula Newton-Leibniz va lua forma .
.Dreptunghiular S.K. Funcție, definită parametric Polyarnaya S.K.
Calcularea ariei figurilor plane
Calcularea lungimii arcului unei curbe plane
Calcularea suprafeței de revoluție
nu este o ecuație diferențială.
poate fi considerată ca o aproximare a ecuației neliniare a unui pendul matematic 
în cazul amplitudinilor mici, când y≈ păcat y.
Unde m- masa corpului, X- coordonatele sale, F(X, t) este forța care acționează asupra corpului cu coordonatele X la momentul t. Soluția sa este traiectoria corpului sub acțiunea forței specificate.
, Valorile funcției și punctele maxime și minime
Cum se procedează în aceste cazuri? Găsiți punctul înalt/jos
Așa este, mai întâi funcția crește, apoi scade - acesta este punctul maxim!
Răspuns: -15 
Raspuns: -2 Găsiți cea mai mare / cea mai mică valoare a unei funcții
.
.Natura locală a extremelor funcției
Căutăm împreună extremele funcției
există și pe întreaga linie numerică. Prin urmare, în acest caz, numai cele la care , adică, servesc ca puncte critice. , de unde și . Puncte critice și împărțiți întregul domeniu al funcției în trei intervale de monotonitate: . Selectăm câte un punct de control în fiecare dintre ele și găsim semnul derivatei în acest punct.
. Prin urmare, graficul său este simetric față de axă Oi iar studiul poate fi efectuat numai pentru intervalul .
și punctele critice ale funcției: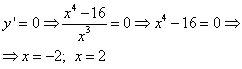
;
,
si determinam semnul acestuia la : obtinem . Deoarece și , atunci este punctul minim al funcției, în timp ce 
.
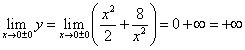
,Continuăm să căutăm împreună extreme ale funcției
y y
la
. Asimptota sa oblică y = x.
.
, deoarece b = const, atunci 
.
, prin urmare,
.
, apoi 
, prin urmare,
.
.
.
.
(1)
.
.
Caracteristică minimă
Ca rezultat, se apelează maximul (minimul) funcției maxim local(minimum local) spre deosebire de maximul absolut (minimul) - cea mai mare (cea mai mică) valoare din domeniul funcției.