KETTŐS INTEGRÁLOK

1. ELŐADÁS

Kettős integrálok.A kettős integrál definíciója és tulajdonságai. Iterált integrálok. Dupla integrálok redukálása ismétlődőkre. Az integráció határainak elrendezése. Dupla integrálok számítása in Descartes-rendszer koordináták.

Kettős integrál a fogalom általánosítása határozott integrál két változós függvény esetén. Ebben az esetben az integrációs szegmens helyett valamilyen lapos ábra lesz.

Legyen D egy zárt korlátos tartomány, és f(x,y) egy tetszőleges függvény, amely ebben a tartományban van definiálva és korlátos. Feltételezzük, hogy a régió határai D véges számú görbéből áll, egyenletek által adott kedves y=f(x) vagy x=g( y), ahol f(x) És g(y) folyamatos függvények.

Osszuk fel a területet D véletlenszerűen bekapcsolva n alkatrészek. Terület én A szakaszt a D szimbólum jelöli s i. Minden szakaszon tetszőlegesen kiválasztunk egy pontot pi,és legyenek koordinátái valamilyen rögzített derékszögű rendszerben ( x i, y i). Komponáljunk integrál összeg funkcióhoz f(x,y) terület szerint D, ehhez minden pontban megtaláljuk a függvény értékeit Pi, megszorozzuk őket a megfelelő Ds szegmensek területeivel énés összegezzük az összes eredményt:

Hívjuk átm(G) terület G a terület határpontjai közötti legnagyobb távolság.

kettős integrál függvények f(x,y) a D tartomány felett az a határ, amelyre az integrálösszegek sorozata hajlik (1.1) a partíciók számának korlátlan növelésével n (ahol). Ez a következőképpen van leírva

Vegye figyelembe, hogy általánosságban elmondható, hogy a for adott funkciótés az adott integrációs terület a terület particionálásának módjától függ Dés pontválasztás Pi. Ha azonban létezik a kettős integrál, akkor ez azt jelenti, hogy a megfelelő integrálösszegek határa már nem függ ezektől a tényezőktől. A kettős integrál létezéséhez(vagy ahogy mondják, így az f függvény(x,y) integrálható a D tartományban), elegendő, ha az integrandus legyen folyamatos az adott integrációs területen.

Hagyja a függvényt f(x,y) integrálható a tartományba D. Mivel az ilyen függvények megfelelő integrálösszegek határa nem függ az integrációs tartomány particionálásának módjától, a particionálás elvégezhető függőleges és vízszintes vonalak használatával. Aztán a régió nagy része D téglalap alakú lesz, amelynek területe D s i=D x i D y i. Ezért a területdifferenciál így írható fel ds=dxdy. Következésképpen, derékszögű koordinátákban, kettős integrálok formába írható

Megjegyzés. Ha az integrand f(x,y)º1, akkor a kettős integrál egyenlő lesz az integrációs régió területével:

Vegye figyelembe, hogy a kettős integrálok ugyanazokkal a tulajdonságokkal rendelkeznek, mint a határozott integrálok. Jegyezzünk meg néhányat.

Kettős integrálok tulajdonságai.

1 0 . Lineáris tulajdonság. A függvényösszeg integrálja egyenlő az integrálok összegével:

a konstans tényező pedig kivehető az integráljelből:

2 0 .Additív tulajdonság. Ha a D integrációs tartományt két részre osztjuk, akkor a kettős integrál egyenlő lesz az egyes részeken lévő integrálok összegével:

3 0 .Az átlagérték tétel. Ha a funkció f( x,y)folytonos a D tartományban, akkor ebben a tartományban van egy ilyen pont(x,h) , mit:

Ekkor felmerül a kérdés: hogyan számítják ki a dupla integrálokat? Hozzávetőlegesen kiszámolható, erre a célra kidolgozva hatékony módszerek a megfelelő integrál összegek összeállítása, amelyeket aztán számítógép segítségével numerikusan kiszámolunk. A kettős integrálok analitikus számításánál két határozott integrálra redukálódnak.

Kettős integrálok tulajdonságai.

A kettős integrálok néhány tulajdonsága közvetlenül következik ennek a fogalomnak a definíciójából és az integrálösszegek tulajdonságaiból, nevezetesen:

1. Ha függvény f(x, y) beépíthető D, azután kf(x, y) ebben a régióban is integrálható, és (24.4)

2. Ha a területen D integrálható funkciók f(x, y)És g(x, y), majd a funkciókat f(x, y) ± g(x, y), és ahol

3. Ha a tartományba integrálható D funkciókat f(x, y)És g(x, y) az egyenlőtlenséget f(x, y)≤g(x, y), azután

(24.6)

Bizonyítsuk be a kettős integrál néhány további tulajdonságát:

4. Ha terület D két területre osztva D 1 és D 2 közös belső pontok és funkció nélkül f(x, y) folyamatos a régióban D, azután

(24.7) Bizonyíték . A terület integrált összege D a következőképpen ábrázolható:

hol van a terület partíciója Dúgy húzzuk meg, hogy a határ között D 1 és D 2 a partíció részeinek határaiból áll. Ekkor a határértékre lépve megkapjuk a (24,7) egyenlőséget.

5. Integrálhatóság esetén be D funkciókat f(x, y) ebben a régióban a függvény is integrálható | f(x, y) |, és az egyenlőtlenség

(24.8)

Bizonyíték.

ahonnan az as határra átlépve megkapjuk a (24.8) egyenlőtlenséget.

6. hol SD– a régió területe D. Ennek az állításnak a bizonyítását úgy kapjuk meg, hogy behelyettesítjük az integrál összegbe f(x, y)≡ 0.

7. Ha integrálható a régióban D funkció f(x, y) kielégíti az egyenlőtlenséget

m ≤ f(x, y) ≤ M,

azután (24.9)

Bizonyíték.

A bizonyítást úgy hajtjuk végre, hogy a nyilvánvaló egyenlőtlenségből a határig haladunk

Következmény.

Ha a (24.9) egyenlőtlenség minden részét elosztjuk azzal D, megkaphatjuk az úgynevezett átlagérték tételt:

Különösen a funkció folytonosságának feltétele mellett f ban ben D van egy ilyen pont ebben a régióban ( x 0, y 0), amelyben f(x 0, y 0) = μ , azaz

-

Az átlagérték tétel másik megfogalmazása.

A kettős integrál geometriai jelentése.

Vegyünk egy testet V, amelyet az egyenlet által megadott felület egy része határol z = f(x, y), kivetítés D ez a felület az O síkhoz HU valamint a felülethatár pontjait a vetületeikkel összekötő függőleges generátorokból nyert oldalirányú hengeres felület.

z=f(x,y)

V

y P i D 2. ábra.

Ennek a testnek a térfogatát fogjuk keresni azon hengerek térfogatösszegének határaként, amelyek alapjai a Δ részek. Si területeken D, a magasságok pedig hosszúságú szegmensek f(Pi), ahol a pontok PiΔ-hez tartoznak Si. Ha elérjük a határértéket, megkapjuk azt

(24.11)

vagyis a kettős integrál a felület által felülről határolt, úgynevezett hengerűr térfogata z = f(x, y), alatta pedig - a terület D.

Kettős integrál kiszámítása iteráltra redukálva.

Vegye figyelembe a területet D vonalak határolják x=a, x=b(a< b ), ahol φ 1 ( x) és φ 2 ( x) folyamatosak a [ a, b]. Ezután bármely, az O koordinátatengellyel párhuzamos egyenest nál nélés áthalad a régió belső pontján D, két ponton keresztezi a régió határát: N 1 és N 2 (1. ábra). Nevezzük ezt a területet helyes be-

nál nél O tengely szabály nál nél. Hasonlóképpen a

y=φ 2 (x) van egy terület az irányban

N 2 tengely O x. A terület megfelelő irányban

Mindkét koordinátatengelyek, mi fogunk

D csak hívd jól. Például,

a megfelelő területet az 1. ábra mutatja.

y=φ 1 (x) N 1

O a b x

Hagyja a függvényt f(x, y) folyamatos a régióban D. Fontolja meg a kifejezést

, (24.12)

hívott kettős integrál funkcióból f(x, y) régiónként D. Először számítsuk ki a változó belső integrálját (zárójelben). nál nél számolás xállandó. Az eredmény az lesz folyamatos funkció tól től x:

A kapott függvényt integráljuk x kezdve de előtt b. Ennek eredményeként megkapjuk a számot

Bizonyítsuk be a kettős integrál egy fontos tulajdonságát.

1. tétel. Ha a terület D, helyesen az O irányba nál nél, két régióra osztva D 1 és D 2 egyenes, párhuzamos az O tengellyel nál nél vagy O tengely x, majd a dupla integrált a régió felett D egyenlő lesz a régiók azonos integráljainak összegével D 1 és D 2:

Bizonyíték.

a) Legyen a sor x = c szünetek D a D 1 és D 2, helyesen az O irányba nál nél. Azután

+

+

b) Legyen a vonal y=h szünetek D a jobb oldalon az O irányába nál nél területeken D 1 és D 2 (2. ábra). Jelölje M 1 (a 1 , h) És M 2 (b 1 , h) az egyenes metszéspontjai y=h szegéllyel L területeken D.

y Vidék D 1-et folyamatos vonalak korlátozzák

y=φ 2 (x) 1) y=φ 1 (x);

D 2 2) görbe DE 1 M 1 M 2 BAN BEN, amelynek egyenletét felírjuk

hM 1 M 2 y=φ 1 *(x), ahol φ 1 *(x) = φ 2 (x) nál nél a ≤ x ≤ a 1 és

A 1 D 1 Bb 1 ≤ x ≤ b, φ 1 *(x) = h nál nél de 1 ≤ x ≤ b 1 ;

3) egyenes x = a, x = b.

Vidék D 2 vonalak korlátozzák y=φ 1 *(x),

A y= φ 2 (x),de 1 ≤ x ≤ b 1 .

y=φ 1 (x) Alkalmazzuk a belső integrálra a következő tételt

az integrációs intervallum felosztása:

O a a 1 b 1 b

+

A kapott integrálok közül a másodikat összegként ábrázoljuk:

+ + .

Amennyiben φ 1 *(x) = φ 2 (x) nál nél a ≤ x ≤ a 1 és b 1 ≤ x ≤ b, akkor a kapott első és harmadik integrál azonos nullával. Következésképpen,

I D = , azaz

Dupla integrálok a próbabábukhoz

Ez a lecke bemutatja a több integrálról szóló kiterjedt témát, amellyel a tanulók általában a második évben találkoznak. dupla és hármas integrálok a laikust nem rosszabbul tudod megfélemlíteni differenciál egyenletek, ezért azonnal foglalkozunk a kérdéssel: nehéz vagy sem? Természetesen egyeseknek nehéz lesz, és őszintén szólva kicsit ravasz voltam a cikk címével - ahhoz, hogy megtanulják a kettős integrálok megoldását, bizonyos készségekre van szükség. Először is, ha integrálokról beszélünk, akkor nyilvánvalóan integrálnunk kell. Logikusan. Ezért a példák elsajátításához tudnia kell találni határozatlan integrálokés kiszámítani határozott integrálok legalábbis átlagos szinten. A jó hír az, hogy maguk az integrálok a legtöbb esetben meglehetősen egyszerűek.

Kinek kell keménynek lennie? Ez érthető. Akik sok sört ittak az első félévben. Mindazonáltal a normál diákokat is megnyugtatom – az oldalon minden szükséges anyag megtalálható a hiányosságok vagy félreértések pótlására. Csak több időt kell töltenie. A tanulmányozandó vagy megismételendő témákra mutató hivatkozásokat a cikkben végig csatoljuk.

A bevezető óra A következő alapvető szempontokat elemezzük lépésről lépésre és részletesen:

– A kettős integrál fogalma

– Integrációs terület. Az integrációs régió megkerülésének sorrendje. Hogyan lehet megváltoztatni a bejárási sorrendet?

Miután JÓL megértette az alapokat, folytathatja a cikket Hogyan kell kiszámítani a kettős integrált? Megoldási példák. Emellett gyakori probléma kb a kettős integrál számítása polárkoordinátákbanés egy tipikus alkalmazás kb lapos korlátos alak súlypontjának megtalálása.

Kezdjük egy létfontosságú kérdéssel – mi az?

A kettős integrál fogalma

Dupla integrált bemenet Általános nézet a következőképpen van írva:

Megértjük a feltételeket és a jelöléseket:
– dupla integrált ikon;
– integrációs terület (lapos ábra);
- két változó integrandusa, gyakran nagyon egyszerű;
- differenciál ikonok.

Mit jelent kettős integrál kiszámítása?

A kettős integrál átlagának kiszámítása keresse meg a NUMBER. A leggyakoribb szám:

És nagyon kívánatos, hogy helyesen találja meg =)

Az eredmény (szám) negatív is lehet. És a nulla is könnyen kiderülhet. Ezen a ponton kifejezetten megálltam, mivel sok diák szorongást tapasztal, amikor a válasz „valami furcsa” lesz.

Sokan emlékeznek arra a "hétköznapi" határozott integrál az is egy szám. Ez itt is ugyanaz. A dupla integrálnak is van egy kiváló geometriai jelentése, de erről később, mindennek megvan a maga ideje.

Hogyan kell kiszámítani a kettős integrált?

A kettős integrál kiszámításához le kell redukálni az ún iterált integrálok. Meg lehet csinálni két út. A leggyakoribb módja a következő:

A kérdőjelek helyett az integráció határait kell kijelölni. Sőt, a külső integrál egyetlen kérdőjelei is számok, és a belső integrál kettős kérdőjelei funkciókat egy "x"-től függő változó.

Hol húzzuk meg az integráció határait? Attól függenek, hogy a probléma állapotában milyen terület van megadva. A terület egy szabályos lapos alak, amellyel sokszor találkoztál, például amikor egy síkfigura területének kiszámítása vagy egy forgástest térfogatának kiszámítása. Hamarosan megtanulja, hogyan kell helyesen beállítani az integráció határait.

Az iterált integrálokra való áttérés után közvetlenül következnek a számítások: először a belső integrált, majd a külsőt veszik fel. Egyik a másik után. Innen a név – iterált integrálok.

Nagyjából a probléma két határozott integrál kiszámítására redukálódik. Amint látod, nem minden olyan nehéz és ijesztő, és ha már elsajátítottad a „hétköznapi” határozott integrált, akkor mi akadályoz meg abban, hogy két integrállal foglalkozz?!

Az iterált integrálokhoz való átvitel második módja valamivel kevésbé gyakori:

Mi változott? Az integráció sorrendje megváltozott: most a belső integrált „x”, a külső integrált pedig „y” helyett. Az integráció korlátai, csillagokkal jelölve - más lesz! A külső integrál egyes csillagai számok, és a belső integrál kettős csillagai inverz függvények"y"-től függően.

Bármelyik módot választjuk is az iterált integrálokra való átvitelre, a végső válasz minden bizonnyal ugyanaz:

Kérem, ne feledje ezt a fontos tulajdonságot, amely többek között a megoldás ellenőrzésére is használható.

Algoritmus a kettős integrál megoldására:

Rendszerezzük az információkat: milyen sorrendben kell megoldani a vizsgált problémát?

1) Be kell fejezni a rajzot. Rajz nélkül a probléma nem oldható meg. Pontosabban úgy dönt, hogy dönt, de ez olyan lesz, mintha vaksakkozna. A rajznak a területet kell ábrázolnia, ami egy lapos figura. Leggyakrabban az ábra egyszerű, és néhány egyenesre, parabolára, hiperbolára stb. korlátozódik. Az órákon egy hozzáértő és gyors rajzkészítési technikát lehet elsajátítani Az elemi függvények grafikonjai és alapvető tulajdonságai, Geometriai diagram transzformációk . Tehát az első lépés a rajz befejezése.

2) Állítsa be az integráció határait, és lépjen az iterált integrálokra.

3) Vegyük a belső integrált

4) Vegyük a külső integrált, és kapjuk meg a választ (számot).

Integrációs régió. Az integrációs régió megkerülésének sorrendje.
Hogyan lehet megváltoztatni a bejárási sorrendet?

Ebben a részben megvizsgáljuk a legfontosabb kérdést - hogyan lehet átmenni az iterált integrálokra és helyesen beállítani az integráció határait. Ahogy fentebb említettük, ezt a következőképpen teheti meg:

Így:

A gyakorlatban ez az egyszerűnek tűnő feladat okozza a legnagyobb nehézséget, a tanulók gyakran összezavarodnak az integráció határainak meghatározásakor. Vegyünk egy konkrét példát:

1. példa

Megoldás:Ábrázoljuk az integrációs területet a rajzon:

A szokásos lapos alak és semmi különös.

Most mindegyikőtöknek adok egy szerszámot - egy ásóbotot, egy lézermutatót. A feladat az árnyékolt terület minden pontjának pásztázása lézersugárral:

A lézersugár áthalad az integrációs tartományon szigorúan alulról felfelé, vagyis MINDIG tarts mutatót lent lapos alak. A nyaláb az x tengelyen keresztül lép be a tartományba, amelyet az egyenlet ad meg, és egy parabolán (piros nyíl) keresztül lép ki a tartományból. A teljes terület megvilágításához szüksége van szigorúan balról jobbra húzza a mutatót a tengely mentén 0-tól 1-ig (zöld nyíl).

Szóval mi történt:
"y" 0-ról ;
Az "x" 0-ról 1-re változik.

A feladatokban a fentiek egyenlőtlenségek formájában vannak felírva:

Ezeket az egyenlőtlenségeket ún az integrációs tartomány megkerülése vagy egyszerűen integráció rendje

Miután kitaláltuk a bejárás sorrendjét, áttérhetünk a kettős integrálról az iterált integrálokra:

A probléma fele megoldódott. Most a második módon kell áttérnünk az iterált integrálokra. Ehhez meg kell találni az inverz függvényeket. Aki elolvasta a lecke második bekezdését A forradalom testének térfogata, könnyebb lesz. Megnézzük a területet beállító funkciókat . Ha ez elég egyszerű, akkor lépjen az inverz függvényekre, ami azt jelenti, hogy „x”-t „y”-ig fejezzük ki. Az egyetlen funkció, ahol van és "x" és "y", egy .

Ha , akkor , és:
az inverz függvény határozza meg a parabola jobb oldali ágát;
az inverz függvény határozza meg a parabola bal oldali ágát.

Gyakran felmerülnek kétségek, például, hogy a függvény határozza meg a parabola bal vagy jobb ágát? Nagyon könnyű eloszlatni a kétségeket: vegyük például a parabola egy pontját (a jobb oldali ágból), és helyettesítsük be a koordinátáit bármely egyenletbe, például ugyanabba az egyenletbe:

A helyes egyenlőséget kapjuk, ami azt jelenti, hogy a függvény pontosan a parabola jobb oldali ágát határozza meg, nem pedig a bal oldalát.

Továbbá, ezt a csekket(mentálisan vagy tervezetben) kívánatos mindig végrehajtani, miután átlépett az inverz függvényekre. Nem lesz semmi, de biztosan megkímél a hibáktól!

A második módon megkerüljük az integráció régióját:

Most tartsa a lézermutatót bal az integráció területéről. A lézersugár áthalad a területen szigorúan balról jobbra. Ebben az esetben a parabola egy ágán keresztül lép be a tartományba, és az egyenlet által megadott egyenesen (piros nyíl) keresztül lép ki a régióból. A teljes terület lézerrel történő beolvasásához mutatót kell rajzolnia a tengely mentén szigorúan alulról felfelé 0-tól 1-ig (zöld nyíl).

Ilyen módon:
az "x" 1-re változik;
Az "y" 0-ról 1-re változik.

A terület megkerülésének sorrendjét egyenlőtlenségek formájában kell felírni:

Ezért az iterált integrálokra való áttérés a következő:

Válasz a következőképpen írható:

Még egyszer emlékeztetek arra, hogy a számítások végeredménye nem attól függ, hogy a kiválasztott terület bejárásának milyen sorrendjét választottuk (ezért teszünk egyenlőségjelet). De előtte végeredmény még messze van, most már csak az a feladatunk, hogy helyesen szabjuk meg az integráció határait.

2. példa

Adott egy kettős integrál az integráció tartományával. Menjen az iterált integrálokhoz, és állítsa be az integráció határait kétféleképpen.

Ez egy „csináld magad” példa. Megfelelően készítsen rajzot és szigorúan kövesse az utasításokat(honnan és hova világítani lézermutatóval). Hozzávetőleges minta a befejezésről a lecke végén.

Gyakrabban tipikus feladat kissé eltérő formában fordul elő:

3. példa

Építsd meg az integráció régióját és

Megoldás: Feltétel szerint a régió megkerülésének első módja adott. A megoldás ismét egy rajzzal kezdődik. Itt nem ezüsttálcán fekszik a terület, de nem nehéz beépíteni. Először is „eltávolítjuk” a függvényeket az integrációs korlátokból: , . A függvény természetesen egy egyenest határoz meg, de mit definiál a függvény? Alakítsuk át egy kicsit:
- egy kör, amelynek középpontja a 2-es sugarú koordináták origójában van. A függvény határozza meg a felső félkört (ne feledje, ha kétségei vannak, mindig helyettesítheti a felső vagy az alsó félkörön fekvő ponttal).

Megnézzük a külső integrál határait: "x" -2-ről 0-ra változik.

Végezzük el a rajzot:

Az érthetőség kedvéért nyilakkal jeleztem a régió megkerülésének első módját, amely megfelel a feltétel iterált integráljainak: .

Most meg kell változtatnunk a terület megkerülésének sorrendjét, ehhez folytatjuk az inverz függvényeket (kifejezzük az "x"-t az "y"-ig):

Nemrég konvertáltuk a függvényt egy kör egyenletévé, majd "x"-et fejezünk ki:
Ennek eredményeként két inverz függvényt kapunk:
- meghatározza a jobb oldali félkört;
- határozza meg a bal oldali félkört.
Ismét, ha kétségei vannak, vegye ki a kör bármely pontját, és derítse ki, melyik a bal és melyik a jobb.

Változtassuk meg a terület bejárási sorrendjét:

A második bypass módszer szerint a lézersugár beleértve a régióba bal a bal oldali félkörön keresztül és jobb oldali kijáratokát a vonalon (piros nyíl). Ezzel egyidejűleg a lézermutatót az y tengely mentén megrajzoljuk felfelé 0-tól 2-ig (zöld nyíl).

Így a terület bejárásának sorrendje a következő:

Általában lehet írni válasz:

4. példa

Ez egy „csináld magad” példa. A példa nem túl bonyolult, de vegye figyelembe, hogy a bejárási sorrend kezdetben a második módon van beállítva! Mi a teendő ilyen esetekben? Először is, a rajzolással van egy nehézség, mivel az inverz függvény grafikonjának megrajzolása még számomra is szokatlan. A következő eljárást javaslom: először kapunk egy „normál” függvényt (az „y”-t „x”-ig fejezzük ki). Ezután elkészítjük ennek a "hétköznapi" függvénynek a grafikonját (mindig építhet legalább pontonként). Ugyanezt tesszük az egyszerűbbekkel is lineáris függvény: -ból kifejezzük az "y"-t és húzunk egy egyenest.

Elemezzük az integráció kezdeti korlátait: balról belépünk a régióba, és azon keresztül kilépünk. Ugyanakkor minden a -1-től 0-ig terjedő "játék" sávban zajlik. Miután meghatározta az integrációs területet a rajzon, nem lesz nehéz megváltoztatni az áthidalás sorrendjét. Példa a megoldásra a lecke végén.

Egy hasonló példát kicsit később részletesebben tárgyalunk.

Még ha mindent tökéletesen értesz is, kérlek ne rohanjon közvetlenül a kettős integrál kiszámításához. A bejárás sorrendje egy trükkös dolog, és nagyon fontos, hogy egy kicsit rájöjjek erre a feladatra, főleg, hogy még nem foglalkoztam mindennel!

Az előző négy példában az integrációs terület teljes egészében az 1., 2., 3. és 4. koordinátanegyedben volt. Mindig ilyen? Nem, természetesen.

5. példa

Módosítsa az integráció sorrendjét

Megoldás: Végezzük el a rajzot, miközben a függvény grafikonja tulajdonképpen egy köbös parabola, csak "az oldalán fekszik":

Régió bejárási sorrend, amely megfelel az iterált integráloknak , nyilak jelzik. Kérjük, vegye figyelembe, hogy a rajz végrehajtása során egy másik limitált ábra is rajzolásra került (az y tengelytől balra). Ezért óvatosnak kell lenni az integrációs terület meghatározásakor - a rossz szám összetéveszthető a területtel.

Térjünk át az inverz függvényekre:
- a számunkra szükséges parabola jobb oldali ága;

Változtassuk meg a terület bejárási sorrendjét. Mint emlékszik, a második bypass módszernél a területet balról jobbra lézersugárral kell pásztázni. De van itt egy érdekesség:

Hogyan kell eljárni ilyen esetekben? Ilyen esetekben az integrációs területet két részre kell osztani, és mindegyik részhez létre kell hozni a saját iterált integráljait:

1) Ha az „y” –1-ről 0-ra változik (zöld nyíl), akkor a sugár egy köbös parabolán keresztül lép be a tartományba, és egy egyenes vonalon (piros nyíl) keresztül lép ki. Ezért a terület bejárásának sorrendje a következő lesz:

2) Ha az "y" 0-ról 1-re változik (barna nyíl), akkor a sugár a parabola egy ágán keresztül lép be a tartományba, és ugyanazon az egyenesen (bíbor nyíl) keresztül lép ki. Ezért a terület bejárásának sorrendje a következő lesz:

És a megfelelő iterált integrálok:

A határozott és többszörös integrálok nagyon kényelmes tulajdonsággal rendelkeznek additívitás, azaz hozzáadhatók, amit ebben az esetben meg kell tenni:
- és itt van a régió megkerülése a második módon, két integrál összege formájában.

Válaszírj így:

Mi a legjobb bypass sorrend? Természetesen a probléma állapotában megadott - a számítások feleannyiak lesznek!

6. példa

Módosítsa az integráció sorrendjét

Ez egy „csináld magad” példa. Félköröket tartalmaz, amelyekkel a 3. példa részletesen foglalkozott. Megoldási minta a lecke végén.

És most az ígért feladat, amikor kezdetben a terület megkerülésének második módja van beállítva:

7. példa

Módosítsa az integráció sorrendjét

Megoldás: Ha a bypass sorrendet a második módon állítjuk be, a rajz megrajzolása előtt célszerű a „normál” funkciókra váltani. Ebben a példában két pácienst kell konvertálni: és .
A lineáris függvény segítségével minden egyszerű:

A függvény grafikonja egy parabola, amely kanonikusságra hivatkozik.

Adjuk meg az "Y"-t "X"-ig:

A parabolának két ágát kapjuk: és . Melyiket válasszam? A legegyszerűbb módja a rajz azonnali végrehajtása. És még akkor is, ha határozottan elfelejtette az analitikus geometria anyagát a paraboláról, akkor is mindkét ágat fel lehet építeni pontszerűen:

Még egyszer szeretném felhívni a figyelmet arra, hogy ezt a rajzot Több lapos figurát kaptam, és nagyon fontos a megfelelő forma kiválasztása! A kívánt ábra kiválasztásában az eredeti integrálok integrálásának korlátai segítenek:
, és ne felejtsük el, hogy az inverz függvény beállítja minden parabola.

Az ábra megkerülését jelző nyilak pontosan megfelelnek az integrálok integrálási határainak .

Hamarosan megtanulja mentálisan elvégezni az ilyen elemzést, és megtalálja a kívánt integrációs területet.

Az alakzat megtalálása után a megoldás utolsó része általában nagyon egyszerű, változtassa meg a terület bejárási sorrendjét:

Az inverz függvényeket már megtaláltuk, és a régió bejárásának szükséges sorrendje:

Válasz:

Utolsó példa egy önálló megoldást szolgáló bekezdésre:

8. példa

Módosítsa az integráció sorrendjét

Komplett megoldásés a válasz a lecke végén.

Elkezdjük megvizsgálni a kettős integrál kiszámításának tényleges folyamatát, és megismerkedünk geometriai jelentésével.

A kettős integrál numerikusan egyenlő egy lapos alakzat területével (integrációs régió). Ez a legegyszerűbb forma kettős integrál, ha két változó függvénye egyenlő eggyel: .

Először nézzük meg általánosságban a problémát. Most meg fog lepődni, milyen egyszerű is valójában! Számítsuk ki egy vonalakkal határolt lapos alak területét. A határozottság kedvéért feltételezzük, hogy az intervallumon. Ennek az ábrának a területe számszerűen egyenlő:

Ábrázoljuk a területet a rajzon:

Válasszuk ki a terület megkerülésének első módját:

Ilyen módon:

És rögtön egy fontos technikai trükk: az iterált integrálokat külön is figyelembe vehetjük. Először a belső integrál, majd a külső integrál. Ez a módszer Kifejezetten ajánlott kezdőknek a teáskannák témakörében.

1) Számítsa ki a belső integrált, miközben az integrációt az "y" változón keresztül hajtja végre:

Határozatlan integrál itt van a legegyszerűbb, majd a banális Newton-Leibniz képletet használjuk, azzal az egyetlen különbséggel, hogy az integráció határai nem számok, hanem függvények. Először a felső határt behelyettesítettük az „y”-be (antiderivatív függvény), majd az alsó határt

2) Az első bekezdésben kapott eredményt be kell cserélni a külső integrálba:

A teljes megoldás tömörebb jelölése így néz ki:

A kapott képlet - pontosan ez a munkaképlet a lapos alakzat területének kiszámításához a "közönséges" határozott integrál segítségével! Lásd a leckét Terület számítása határozott integrál segítségével, ott van minden lépésnél!

Azaz, a terület kiszámításának problémája kettős integrál segítségével kicsit más a terület keresésének problémájából egy határozott integrál segítségével! Valójában egy és ugyanaz!

Ennek megfelelően semmiféle nehézség nem merülhet fel! Nem fogok sok példát figyelembe venni, mivel Ön valójában többször is találkozott ezzel a problémával.

9. példa

A kettős integrál segítségével számítsa ki egy vonallal határolt síkidom területét.

Megoldás:Ábrázoljuk a területet a rajzon:

Az ábra területét a kettős integrál segítségével számítjuk ki a következő képlet szerint:

Válasszuk a régió bejárásának sorrendjét:

Itt és az alábbiakban nem térek ki arra, hogyan kell bejárni egy területet, mert az első bekezdés nagyon részletes volt.

Ilyen módon:

Amint már megjegyeztem, a kezdőknek jobb, ha az iterált integrálokat külön számítják ki, ugyanazt a módszert fogom követni:

1) Először a Newton-Leibniz képlet segítségével foglalkozunk a belső integrállal:

2) Az első lépésben kapott eredményt behelyettesítjük a külső integrálba:

A 2. pont valójában egy lapos figura területének meghatározása egy határozott integrál segítségével.

Válasz:

Itt van egy ilyen ostoba és naiv feladat.

Egy érdekes példa egy független megoldásra:

10. példa

A kettős integrál segítségével számítsa ki egy síkidom területét, amelyet a vonalak határolnak, ,

Példa a végső megoldásra a lecke végén.

A 9-10. példákban sokkal jövedelmezőbb a terület megkerülésének első módszere, a kíváncsi olvasók egyébként megváltoztathatják az elkerülés sorrendjét, és a második módon számíthatják ki a területeket. Ha nem hibázik, akkor természetesen ugyanazokat a területértékeket kapja meg.

Két változó függvényéhez, amelyet a következőképpen határozunk meg z = f(x, y) .

A kettős integrált a következőképpen írjuk fel:

Itt D- egyenesekkel határolt lapos alakzat, melynek kifejezéseit (egyenlőségeit) a kettős integrál számítási feladatában adjuk meg. Bal és jobb - egyenlőségek, amelyben a változó a bal oldalon x, és fent és lent - egyenlőségekkel, amelyben a bal oldalon lévő változó y. Ez a hely és tovább az egyik legfontosabb a kettős integrál számítási technikájának megértéséhez.

Dupla integrál kiszámítása - azt jelenti, hogy egy számot keresünk, amely megegyezik az említett ábra területével D .

Amíg meg nem érintjük a kettős integrál definíciói , és megtanuljuk kiszámolni. Könnyebb megérteni, mi az a kettős integrál, ha több feladatot is megoldott a kiszámításához, így a lecke végén megtalálja a dupla integrál definícióját. Kicsit előre tekintve csak annyit jegyezhetünk meg, hogy az említett ábrához a kettős integrál definíciója is társul D .

Ha az ábra D egy téglalap, az azt határoló összes vonal egyenes. Ha az ábra D- görbe vonalú, majd balról és jobbról egyenes vonalak, felülről és alulról pedig - a feladatban megadott egyenlőségekkel megadott görbe vonalak határolják. Vannak olyan esetek is, amikor egy figura D- egy háromszög, de az ilyen esetekről kicsit távolabb.

A kettős integrál kiszámításához tehát rendezni kell az ábrát határoló vonalakat D, amelynek szigorú neve van - az integráció régiója. Rendezés balra és jobbra, valamint felülre és lentre. Erre akkor lesz szükség a kettős integrál redukálása iterált integrállá – a kettős integrál számítási módja.

Téglalap alakú eset:

Görbe vonalú régió esete:

Ez pedig már a számunkra ismert határozott integrálok megoldása, melyben az integráció felső és alsó határa van rögzítve. Olyan kifejezések, amelyek egy alakzatot kötő vonalakat határoznak meg D, a szokásos határozott integrálok integrálásának határai lesznek, amihez már közeledünk.

A kettős integrál redukálása iterálttá

Téglalap alakú tok

Legyen egy ilyen függvénynek kettős integrálja

Nak nek számítsuk ki ezt a kettős integrált , redukálnia kell az iterált integrálra, amelynek van alakja

.

Először a belső (jobb) határozott integrált kell kiszámítani, majd a külső (bal) határozott integrált.

Szerepeket válthatsz xÉs y

.

1. példa Dupla integrál kiszámítása

A belső (jobboldali) integrált y állandónak tekintve számítjuk ki. Kapunk.

.

2. példa Dupla integrál kiszámítása

,

Megoldás. Ezt a kettős integrált redukáljuk az iterált integrálra

A rajzon felépítjük az integrációs területet:

Most kiszámítjuk a külső (bal) integrált az éppen számított belső (jobb) integrálból:

Az eredmény ennek a kettős integrálnak a megoldása lesz.

Számítsa ki saját maga a dupla integrált, majd nézze meg a megoldást

Görbe vonalú vagy háromszög alakú régió eset

Legyen ismét két változó függvénye f(x, y) és a korlátozások D: kicsit másképp néz ki:

Ez a bejegyzés azt jelenti, hogy az ábra D határ a bal és a jobb oldalon, mint egy egyenes vonalú régió esetében - egyenes vonalak x = aÉs x = b, de alatta és felett vannak a görbék, amelyeket a és egyenletek adnak meg. Más szóval, és funkciók.

Legyen egy ilyen függvénynek kettős integrálja is

Ennek a kettős integrálnak a kiszámításához redukálnunk kell az iterált integrálra, amelynek alakja van

.

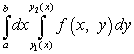Itt vannak az integráció határai aÉs b számok, és és függvények. Háromszög alakú régió esetén az egyik függvény vagy az egyenes egyenlete. Ezt az esetet a 3. példa tárgyalja.

Mint egy egyenes tartomány esetében, először ki kell számítani a jobb oldali határozott integrált, majd a bal oldali határozott integrált.

Ugyanígy válthat szerepeket is. xÉs y. Ekkor az iterált integrál alakja lesz

.

Egy ilyen iterált integrált pontosan ugyanúgy kell megoldani: először a belső (jobboldali), majd a külső (bal) integrált.

5. példa Dupla integrál kiszámítása

,

Megoldás. Ezt a kettős integrált redukáljuk az iterált integrálra

.

A rajzon felépítjük az integrációs területet, és látjuk, hogy háromszög alakú:

Kiszámítjuk a belső (jobboldali) integrált, x-et állandónak tekintve. Kapunk.

Most kiszámítjuk az éppen számított belső (jobb) integrál külső (bal) integrálját. Először is ezt az integrált integrálok összegeként ábrázoljuk:

.

Kiszámoljuk az első tagot:

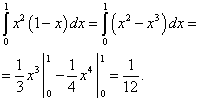
Kiszámoljuk a második tagot:

Kiszámoljuk a harmadik tagot:

Megkapjuk az összeget, ami ennek a kettős integrálnak a megoldása:

.

6. példa Dupla integrál kiszámítása

Megoldás. Ezt a kettős integrált redukáljuk az iterált integrálra

A rajzon felépítjük az integrációs területet:

Kiszámítjuk a belső (jobboldali) integrált, x-et állandónak tekintve. Kapunk.

.

Most kiszámítjuk a külső (bal) integrált az éppen számított belső (jobb) integrálból:

Az eredmény ennek a kettős integrálnak a megoldása lesz.

x- jó és rossz y- az integráció helyes és helytelen tartományai

Előfordul, hogy a kettős integrál integrálási területét olyan vonalak korlátozzák, hogy szükségessé válik az integrációs terület részekre osztása, és az egyes megfelelő iterált integrálok külön-külön történő megoldása. Ezek azok az esetek, amikor:

1) az integrációs terület olyan ábra, amely két vagy több egyenes vagy ívelt vonallal rendelkezik alsó vagy felső (bal vagy jobb) határ formájában;

2) az integrálási terület olyan alakzat, amelynek határát az egyenesek több mint két pontban metszik.

Ha a fentiek az integrációs régió bal vagy jobb oldali határára vonatkoznak, vagyis a vonalak által megadott korlátozásokra. x, akkor az integráció tartománya ún x- rossz. Ha egy egyenes y = y0 csak egy pontban metszi a megfelelő határt, és ha csak egy egyenes vagy görbe szolgál határként, akkor az integrációs tartományt ún. x-helyes

Hasonlóképpen, ha a vonalak által meghatározott határt kifejezve y, egyenes x = x0 több pontban metszi egymást, vagy ha egynél több egyenes vagy görbe szolgál határként, akkor az integrációs területet ún. y- rossz. Hozza ki a jeleket most y-a megfelelő terület, feltehetően egész egyszerűen.

Eddig példákat vettünk figyelembe x- hibás és y-rendszeres integrációs területek. Tekintsük most azokat az eseteket, amikor a helyességi feltételt megsértik.

7. példa Számítson ki egy kettős integrált, amelynek integrálási területét vonalak korlátozzák y = x , xy = 1 , y = 2 .

Megoldás. Az integráció területe az y-hibás, mivel az alsó szegélye nem állítható egy sorral y = y(x) . Amint a fenti ábrán látható, az alsó korlát a következőkből áll y = x(sötét gesztenyebarna) és xy= 1 (zöld). Ezért közvetlen x= 1 (fekete) az integrációs területet két részre oszthatjuk - és .

Ezt a kettős integrált a következőképpen számítjuk ki:

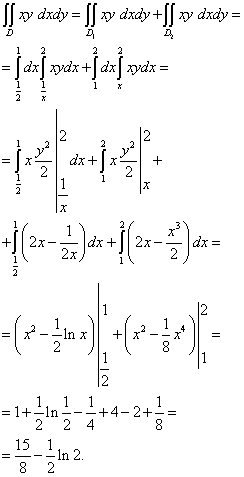
Az integráció sorrendjének megváltoztatása

Ahogy fentebb megjegyeztük, miután a dupla integrált redukáltuk az iterált integrálra, megváltoztathatjuk a változókat xÉs y szerepeket, vagy más szóval megváltoztatja az integráció sorrendjét.

Az integráció sorrendjének változását képletesen O "Henry" szavaival írhatjuk le: Így viselkedik a dzsungel lakója - a ketrecbe kerülve a fenevad, és így viselkedik a ketrec lakója. - egy férfi, elveszett a kétségek dzsungelében." Az eredmény, O" Henry szerint is, egy és ugyanaz: "Chalmers ezer apró darabra tépte a levelet, és gyötörni kezdte drága szőnyegét, visszafelé lépdelve és tovább." ( O.Henry. Scheherazade a Madison Square-ről.)

Ekkor, ha a bal oldali integrál van a változó felett x, és a megfelelőt y, akkor az integráció sorrendjének megváltoztatása után minden fordítva lesz. Ekkor az "új" y integrálási határait a "régi" x-ből kell "kölcsönvenni", az "új" x integrálási határait pedig az alábbi formában kell megkapni. inverz függvény, az egyenlet feloldása x-hez képest, amely y határértéket szab.

8. példa

.

Megoldás. Az integrálási sorrend megváltoztatása után az y feletti integrál balra, az x feletti integrál pedig jobbra. Az „új” játékos integrációs határait a „régi” X-től fogjuk kölcsönkérni, vagyis az alsó határ nulla, a felső határ pedig egy. A "régi" játékos integrációjának határait a és az egyenletek adják meg. Miután megoldottuk ezeket az egyenleteket x-re vonatkozóan, új integrációs határértékeket kapunk x-re:

(alsó) és (felső).

Így az integráció sorrendjének megváltoztatása után az iterált integrál a következőképpen lesz írva:

.

A kettős integrálban az integráció sorrendjének megváltoztatása után az integrációs tartomány gyakran átalakul y- rossz ill x- helytelen (lásd az előző bekezdést). Ezután az integrációs tartományt részekre kell bontani, és minden megfelelő iterált integrált külön kell megoldani.

Mivel az integrációs tartomány részekre bontása sok tanuló számára nehézségekbe ütközik, nem szorítkozunk az előző bekezdésben szereplő példára, hanem elemezünk még néhány példát.

9. példa Módosítsa az iterált integrál integrációs sorrendjét

.

Megoldás. Tehát ennek az iterált integrálnak az integrációs területét az egyenes vonalak korlátozzák y = 1 , y = 3 , x = 0 , x = 2y .

Más sorrendben történő integrálás esetén a régió alsó határa két egyenesből áll: ABÉs időszámításunk előtt, amelyeket az egyenletek adnak meg y= 1 és y = x/2 , ami az alábbi ábrán látható.

Az ilyen bizonytalanságból való kiút az integrációs tartomány két részre osztása. Az integrációs területet egyenes vonal osztja fel BM. Az új integrációs határértékek kiszámítása kereséssel történik inverz függvény. E megoldás szerint az iterált integrál az integrálási sorrend megváltoztatása után egyenlő lesz két integrál összegével:

Természetesen a kettős integrál megoldása is ugyanaz lesz, ami a példa feltételében megadott iterált integrálra redukálódik.

10. példa Módosítsa az iterált integrál integrációs sorrendjét

.

Megoldás. Tehát az iterált integrál integrálási területét az egyenesek korlátozzák x = 0 , x= 2 és görbék és .

Amint az alábbi ábrán látható, a tengellyel párhuzamos egyenes 0x, több mint két pontban metszi az integrációs régió alsó határát.

Ezért az integrációs tartományt három részre osztjuk egyenes vonalakkal, amelyek az ábrán feketével vannak megrajzolva. Az új integrációs határértékek kiszámítása az inverz függvény meghatározásával történik. Az integráció három új területére a korlátok a következők lesznek.

E megoldás szerint az ismétlődő integrál az integrálási sorrend megváltoztatása után három integrál összegével egyenlő:

Három integrálnak ugyanaz az összege lesz egyenlő a kettős integrállal, amely a példa feltételében megadott iterált integrálra redukálódik.

Mégis, a vis maior körülmények gyakran már az előző lépésnél – a beilleszkedés határainak meghatározásánál – zavarják a tanulókat. A szorongás és a zavarodottság nem minden alapot nélkülöz: ha az integrációs tartomány részekre bontásához általában elég a rajzra nézni, és megoldani az iterált integrált - az integrálok táblázatát, akkor a határok felállításában némi gyakorlati tapasztalat szükséges. integráció. Fussunk végig egy példát, amelyben csak az integráció határainak elrendezésén és - szinte automatikusan - a régió felosztásán időzünk, és mellőzzük magát a megoldást.

11. példa. Keresse meg a kettős integrál integrálásának határait, ha az integráció területe D a következőképpen állítsa be:

y - 2x ≤ 0;
2y - x ≥ 0;
xy ≤ 2.

Megoldás. kifejezetten (via xÉs y"szennyeződések nélkül") az integrálási területet korlátozó vonalak nincsenek megadva. Mivel x esetén ezek leggyakrabban egyenesek, amelyek egy ponton érintik az y-n keresztül kifejezett felső és alsó határt, akkor pontosan ezen az úton haladunk. Sőt, az integráció sorrendjének megváltoztatásakor egy azonos területű integrációs területet kapunk. Oldjuk meg a játékos egyenlőtlenségeit, és kapjuk:

y ≤ 2x;
y ≥ x/2;
y ≤ 2/x.

A kapott vonalakat ráépítjük a rajzra. Az x-hez viszonyított integráció határai valóban a vonalak x= 0 és x= 2. De az integráció régiója az lett y-hibás, mivel a felső határa nem állítható egy sorral y = y(x) .

1.1 A kettős integrál definíciója

1.2 A kettős integrál tulajdonságai

A kettős integrál tulajdonságai (és származtatásuk) hasonlóak az egyetlen határozott integrál megfelelő tulajdonságaihoz.

1°. Additivitás. Ha az f(x, y) függvény integrálható a D tartományba, és a D tartományt egy nulla területű Г görbe osztja fel két összefüggő D 1 és D 2 tartományra, közös belső pontok nélkül, akkor az f(x, y) mindegyikbe integrálható a D1 és D2 régióból, és

2°. Lineáris tulajdonság. Ha az f(x, y) és g(x, y) függvények integrálhatók a D tartományban, mi? És? - Bármi valós számok, akkor a [? f(x, y) + ? g(x, y)] szintén integrálható a D tartományba, és

3°. Ha az f(x, y) és g(x, y) függvények integrálhatók a D tartományban, akkor ezen függvények szorzata is integrálható D tartományban.

4°. Ha az f(x, y) és g(x, y) függvények egyaránt integrálhatók a D tartományban és mindenhol ebben az f(x, y) tartományban? g(x, y), akkor

5°. Ha az f(x, y) függvény integrálható a D tartományba, akkor az |f(x, y)| integrálható a D tartományba, és

(Természetesen az |f(x, y)| integrálhatósága D-ben nem jelenti az f(x, y) integrálhatóságát D-ben.)

6°. Az átlagérték tétel. Ha mindkét f(x, y) és g(x, y) függvény integrálható egy D tartományban, akkor a g(x, y) függvény nem negatív (nem pozitív) mindenhol ebben a tartományban, M és m a az f( x, y) függvény legjobb felső és alsó korlátja a D tartományban, akkor van egy szám, amely kielégíti az m egyenlőtlenséget? ? ? M és olyan, hogy a képlet

Konkrétan, ha az f(x, y) függvény folytonos D-ben, és a D tartomány összefügg, akkor ebben a tartományban van egy ilyen pont (?, ?), mi? = f(?, ?), és a képlet így alakul

7°. Fontos geometriai tulajdonság. megegyezik a D régió területével

Legyen adott egy T test a térben (2.1. ábra), amelyet alulról a D tartomány határol, felülről - egy folytonos és nem negatív függvény grafikonja) z \u003d f (x, y,) amely definiált a D tartományban oldalról - egy hengeres felülettel, melynek vezetõje a D határtartomány, és a generátorok párhuzamosak az Óz tengellyel. Az ilyen típusú testet hengeres testnek nevezzük.

1.3 A kettős integrál geometriai értelmezése

1.4 A téglalap kettős integráljának fogalma

Legyen egy tetszőleges f(x, y) függvény definiálva mindenhol az R = téglalapon? (Lásd 1. ábra).

Osszuk fel az a szegmenst? x? b-t n részszakaszra az a = x 0 pontok felhasználásával< x 1 < x 2 < ... < x n = b, а сегмент c ? y ? d на p частичных сегментов при помощи точек c = y 0 < y 1 < y 2 < ... < y p = d.

Ez a felosztás vonalak segítségével, párhuzamos a tengelyekkel Ox és Oy, megfelel az R téglalap felosztásának n · p részleges téglalapokra R kl = ? (k = 1, 2, ..., n; l = 1, 2, ..., p). Az R téglalap meghatározott partícióját a T szimbólum jelöli. A továbbiakban ebben a részben a "téglalap" kifejezés olyan téglalapot jelent, amelynek oldalai párhuzamosak a koordinátatengelyekkel.

Minden R kl részleges téglalapon kiválasztunk egy tetszőleges pontot (? k , ? l). Ha?x k = x k - x k-1 , ?y l = y l - y l-1 , akkor? R kl-lel jelöljük az R kl téglalap területét. Nyilvánvaló, hogy ?R kl = ?x k ?y l .

Az R téglalap adott T partíciójának megfelelő f(x, y) függvény és a T partíció résztéglalapjain lévő közbülső pontok (?k, ?l) adott megválasztott összegének nevezzük.

Az átlót az R kl téglalap átmérőjének nevezzük. Egy szimbólum? jelölje az összes R kl részleges téglalap átmérője közül a legnagyobbat.

Az I számot az integrálösszegek határának (1) nevezzük? > 0, ha bármely pozitív számra? ezt megadhatja pozitív szám?, miben?< ? независимо от выбора точек (? k , ? l) на частичных прямоугольниках R выполняется равенство

| ? - Én |< ?.

Egy f(x, y) függvényt integrálhatónak nevezünk (Riemann szerint) egy R téglalapon, ha van véges I határa ennek a függvénynek az integrálösszegeinek at? > 0.

Ezt az I határértéket az f(x, y) függvény kettős integráljának nevezzük az R téglalap felett, és a következő szimbólumok egyikével jelöljük:

Megjegyzés. Ugyanúgy, mint az egyszeri határozott integrálnál, megállapítható, hogy az R téglalapra integrálható f(x, y) függvény erre a téglalapra korlátos.

Ez csak a következőkben ad okot a mérlegelésre korlátozott funkciók f(x, y).