Egy végtelenül kicsi érték határa. Példák

A Wikipédiából, a szabad enciklopédiából

Elenyésző - numerikus függvény vagy nullára hajló sorozat.

végtelenül nagy- egy numerikus függvény vagy sorozat, amely egy bizonyos előjel végtelenségébe hajlik.

Infinitezimálisok és nagyok számítása

Infinitezimális számítás- infinitezimális értékekkel végzett számítások, amelyekben a származtatott eredményt végtelenül kicsinyek végtelen összegének tekintjük. Az infinitezimális számítás az általános koncepció differenciál- és integrálszámításhoz, amelyek a modern felsőbb matematika alapját képezik. Az infinitezimális mennyiség fogalma szorosan összefügg a határ fogalmával.

Elenyésző

Utóbbi $a_n$ hívott elenyésző, ha $\lim\limits_(n\to\infty)a_n=0$ . Például a számsor $a_n=\dfrac(1)(n)$ - végtelenül kicsi.

A függvényt hívják végtelenül kicsi egy pont szomszédságában $x_0$ , ha $\lim\limits_(x\to x_0)f(x)=0$ .

A függvényt hívják végtelenül kicsi a végtelenben, ha $\lim\limits_(x\to+\infty)f(x)=0$ vagy $\lim\limits_(x\to-\infty)f(x)=0$ .

Szintén végtelenül kicsi az a függvény, amely a függvény és a határértéke közötti különbség, vagyis ha $\lim\limits_(x\to+\infty)f(x)=a$ , akkor $f(x)-a=\alpha(x)$ , $\lim\limits_(x\to+\infty)(f(x)-a)=0$ .

Hangsúlyozzuk, hogy az infinitezimális értéket változó értékként (függvényként) kell érteni, amely csak a változás folyamatában[amikor törekszik $x$ nak nek $a$ (tól től $\lim\limits_(x\to a)f(x)=0$ )] kisebb, mint egy tetszőleges szám ( $\varepsilon$ ). Ezért például egy olyan állítás, mint "egy milliomod végtelenül kicsi érték", nem igaz: nincs értelme azt mondani egy számról [abszolút értékről], hogy az végtelenül kicsi.

végtelenül nagy

Az összes alábbi képletben az egyenlőségtől jobbra lévő végtelenség egy bizonyos jelet jelent ("plusz" vagy "mínusz"). Ez például a függvény $x\sin x$ , mindkét oldalon korlátlan, nem végtelenül nagy a $x\to+\infty$ .

Utóbbi $a_n$ hívott végtelenül nagy, ha $\lim\limits_(n\to\infty)a_n=\infty$ .

A függvényt hívják végtelenül nagy egy pont szomszédságában $x_0$ , ha $\lim\limits_(x\to x_0)f(x)=\infty$ .

A függvényt hívják végtelenül nagy a végtelenben, ha $\lim\limits_(x\to+\infty)f(x)=\infty$ vagy $\lim\limits_(x\to-\infty)f(x)=\infty$ .

Akárcsak a végtelen kicsinyeknél, itt is meg kell jegyezni, hogy a végtelenül nagy mennyiség egyetlen értéke sem nevezhető "végtelenül nagynak" – a végtelenül nagy mennyiség olyan függvény, a változás folyamatában nagyobb lehet egy tetszőleges számnál.

Az infinitezimálisok tulajdonságai

Véges számú, végtelenül kicsi függvény algebrai összege végtelen kis funkció.
Az infinitezimálisok szorzata végtelenül kicsi.
Egy infinitezimális sorozat és egy korlátos sorozat szorzata végtelenül kicsi. Következésképpen az infinitezimális konstans szorzata infinitezimális.
Ha egy $a_n$ - végtelenül kis sorozat, amely megőrzi a jelet, akkor $b_n=\dfrac(1)(a_n)$ egy végtelenül nagy sorozat.

Infinitezimálisok összehasonlítása

Definíciók

Tegyük fel, hogy ugyanerre infinitezimálisaink vannak $x\to a$ mennyiségeket $\alpha(x)$ és $\beta(x)$ (vagy ami a definíció szempontjából nem fontos, infinitezimális sorozatok).

Ha egy $\lim\limits_(x\to a)\dfrac(\beta)(\alpha)=0$ , akkor $\beta$ - végtelenül kicsi magasabb rendű kicsinység, hogyan $\alpha$ . kijelöl $\beta=o(\alpha)$ vagy $\beta\prec\alpha$ .
Ha egy $\lim\limits_(x\to a)\dfrac(\beta)(\alpha)=\infty$ , akkor $\beta$ - végtelenül kicsi a legkisebb rendű kicsinység, hogyan $\alpha$ . Illetőleg $\alpha=o(\béta)$ vagy $\alpha\prec\beta$ .
Ha egy $\lim\limits_(x\to a)\dfrac(\beta)(\alpha)=c$ (a határ véges és nem egyenlő 0-val), akkor $\alpha$ és $\beta$ végtelenül kicsi mennyiségek egy nagyságrenddel. Ezt így jelöljük $\alpha\asymp\beta$ vagy kapcsolatok egyidejű végrehajtásaként $\beta=O(\alpha)$ és $\alpha=O(\béta)$ . Megjegyzendő, hogy egyes forrásokban találkozni lehet olyan megjelöléssel, amikor a parancsok azonosságát egyetlen „big o” reláció formájában írják le, ami ennek a szimbólumnak a szabad használata.
Ha egy $\lim\limits_(x\to a)\dfrac(\beta)(\alpha^m)=c$ (a határ véges és nem egyenlő 0-val), akkor az infinitezimális mennyiség $\beta$ Megvan $m$ -a kicsinységi sorrend viszonylag végtelenül kicsi $\alpha$ .

Az ilyen határértékek kiszámításához célszerű a L'Hospital szabályát használni.

Összehasonlítási példák

Nál nél $(x\-0)$ nagyságrendű $x^5$ Megvan magasabb rendű kicsinysége ahhoz képest $x^3$ , mert $\lim\limits_(x\to 0)\dfrac(x^5)(x^3)=0$ . Másrészről, $x^3$ tekintetében a legalacsonyabb kicsinységi rendű $x^5$ , mert $\lim\limits_(x\to 0)\dfrac(x^3)(x^5)=\infty$ .

Használata O-a kapott eredmények szimbólumai a következő formában írhatók fel

x^5=o(x^3)

$\lim\limits_(x\to 0)\dfrac(2x^2+6x)(x)=\lim\limits_(x\to 0)\dfrac(2x+6)(1)=\lim\limits_(x) \to 0)(2x+6)=6,$ vagyis mikor $x\-től 0-ig$ funkciókat $f(x)=2x^2+6x$ és $g(x)=x$ azonos rendű végtelenül kicsi mennyiségek.

Ebben az esetben a bejegyzések

2x^2+6x = O(x)

és

x = O(2x^2+6x).

Nál nél $(x\-0)$ elenyésző $2x^3$ tekintetében a harmadik kicsinységi renddel rendelkezik $x$ , mert a $\lim\limits_(x\to 0)\dfrac(2x^3)(x^3)=2$ , végtelenül kicsi $0(,)7x^2$ - másodrendű, végtelenül kicsi $\sqrt(x)$ - rendelés 0,5.

Egyenértékű mennyiségek

Meghatározás

Ha egy $\lim\limits_(x\to a)\dfrac(\beta)(\alpha)=1$ , akkor végtelenül kicsi vagy végtelenül nagy mennyiségeket $\alpha$ és $\beta$ hívott egyenértékű(jelölése: $\alpha\thicksim\beta$ ).

Nyilvánvaló, hogy az ekvivalens mennyiségek a végtelenül kicsi (végtelenül nagy) azonos kicsinységi nagyságrendű mennyiségek speciális esetei.

Nál nél a következő ekvivalencia viszonyok érvényesek (az ún. figyelemre méltó határok következtében):

$\sin\alpha(x)\thicksim\alpha(x);$
$\mathrm(tg)\,\alpha(x)\thicksim\alpha(x);$
$\arcsin(\alpha(x))\thicksim\alpha(x);$
$\mathrm(arctg)\,\alpha(x)\thicksim\alpha(x);$
$\log_a(1+\alpha(x))\thicksim\alpha(x)\cdot\frac(1)(\ln(a))$ , ahol $a>0$ ;
$\ln(1+\alpha(x))\thiksim\alpha(x);$
$a^(\alpha(x))-1\vastagság\alpha(x)\cdot\ln(a)$ , ahol $a>0$ ;
$e^(\alpha(x))-1\thixim\alpha(x);$
$1-\cos(\alpha(x))\thiksim\frac(\alpha^2(x))(2);$
$(1+\alpha(x))^\mu-1\thiksim\mu\cdot\alpha(x),\quad\mu\in\R$ , ezért használja a következő kifejezést:

\sqrt[n](1+\alpha(x))\approx\frac(\alpha(x))(n)+1

, ahol

\alpha(x)\xjobbra nyíl()0

Tétel

Két végtelenül kicsi vagy végtelenül nagy mennyiség hányadosának (arányának) határa nem változik, ha az egyiket (vagy mindkettőt) egy ekvivalens értékre cseréljük.

Ennek a tételnek gyakorlati jelentősége van a határok megtalálásában (lásd a példát).

Példák a felhasználásra

megtalálja $\lim\limits_(x\to 0)\dfrac(\sin 2x)(x).$

Csere

\sin 2x

egyenértékű érték

2x

, kapunk

\lim\limits_(x\to 0)\dfrac(\sin 2x)(x)=\lim\limits_(x\to 0)\dfrac(2x)(x)=2.

megtalálja $\lim\limits_(x\to\frac(\pi)(2))\dfrac(\sin(4\cos x))(\cos x).$

Mert

\sin(4\cos x)\thicksim(4\cos x)

nál nél

x\to\dfrac(\pi)(2)

kapunk

\lim\limits_(x\to \frac(\pi)(2))\dfrac(\sin(4\cos x))(\cos x)=\lim\limits_(x\to\frac(\pi) (2))\dfrac(4\cos x)(\cos x)=4.

Kiszámítja $\sqrt(1(,)2)$ .

A képlet segítségével:

\sqrt(1(,)2)\approx 1+\frac(0(,)2)(2)=1(,)1

, számológép használata közben (pontosabb számítások) a következőket kaptuk:

\sqrt(1(,)2)\kb. 1(,)095

, így a hiba 0,005 (kevesebb, mint 1%) volt, vagyis a módszer egyszerűsége miatt hasznos egyhez közeli számtani gyökök durva becslésével.

Sztori

Old school matematikusok vetették alá a koncepciót elenyésző kemény kritika. Michel Rolle azt írta, hogy az új kalkulus: ragyogó hibák halmaza»; Voltaire mérgezően rámutatott, hogy ez a számítás az olyan dolgok kiszámításának és pontos mérésének művészete, amelyek létezését nem lehet bizonyítani. Még Huygens is elismerte, hogy nem értette a magasabb rendű különbségek jelentését.

A sors iróniájának tekinthető a 20. század közepén a nem szabványos elemzések megjelenése, amely bebizonyította, hogy az eredeti nézőpont - a tényleges infinitezimálisok - is konzisztens és az elemzés alapja lehet. A nem szabványos elemzés megjelenésével világossá vált, hogy a 18. századi matematikusok miért illegálisan végeztek a klasszikus elmélet akciók azonban megfelelő eredményt hoztak.

Lásd még

Írjon véleményt a "Végtelenül kicsi és végtelenül nagy" cikkről

Megjegyzések

Irodalom

// Brockhaus és Efron enciklopédikus szótára: 86 kötetben (82 kötet és további 4 kötet). - Szentpétervár. , 1890-1907.

A végtelenül kicsi és a végtelenül nagyot jellemző részlet

- Nos, barátom, attól tartok, hogy te és a szerzetes elpazarolod a puskaporodat - mondta Andrej herceg gúnyosan, de szeretettel.
- Ah! mon ami. [DE! Barátom.] Csak imádkozom Istenhez, és remélem, hogy meghallgat. Andre – mondta félénken egy pillanatnyi csend után –, van egy nagy kérésem önhöz.
- Mi, barátom?
Nem, ígérd meg, hogy nem utasítod vissza. Nem kerül semmi munkába, és nem lesz benne semmi méltatlan. Csak te tudsz megvigasztalni. Ígérd meg, Andryusha – mondta, kezét az erszényébe dugva és benne valamit tartva, de még nem mutatta meg, mintha a kérés tárgya lenne, amit tart, és mintha az ígéret megérkezése előtt a kérés teljesítéseként nem tudta kivenni a táskából. Ez valami.
Félénken, könyörgőn nézett bátyjára.
„Ha ez sok munkámba kerülne…” – válaszolta Andrej herceg, mintha sejtené, mi a baj.
- Amit akarsz, gondolj! Tudom, hogy ugyanolyan vagy, mint mon pere. Gondolj, amit akarsz, de tedd meg helyettem. Légyszives csináld! Apám apja, a nagyapánk, minden háborúban viselte... - Még mindig nem vette ki a táskájából, amit tartott. – Szóval megígéred?
– Hát persze, mi a baj?
- Andre, megáldalak a képpel, és megígéred, hogy soha nem veszed le. Ígéret?
„Ha nem húzza le két fontra a nyakát... Hogy a kedvében járjon...” – mondta Andrej herceg, de ugyanabban a pillanatban, amikor észrevette, hogy nővére e tréfálkozáskor elszomorodott, megbánta. „Nagyon örülök, nagyon örülök, barátom” – tette hozzá.
„Akaratod ellenére megment, megkönyörül rajtad, és magához fordít, mert egyedül Őbenne van az igazság és a béke” – mondta az izgalomtól remegő hangon, két kézzel maga elé tartott ünnepélyes mozdulattal. testvér a Megváltó ovális ősi ikonja, fekete arccal, ezüst ládában, finom megmunkálású ezüst láncon.
Keresztet vetett, megcsókolta az ikont, és átnyújtotta Andreynek.
– Kérlek, Andre, nekem…
Nagy szeméből kedves és félénk fénysugár ragyogott. Ezek a szemek megvilágították az egész beteges, vékony arcot, és gyönyörűvé tették. A testvér el akarta venni a skapulárt, de a lány megállította. Andrej megértette, keresztet vetett, és megcsókolta az ikont. Az arca egyszerre volt szelíd (meghatódott) és gúnyos.
- Merci, mon ami. [Köszönöm barátom.]
Megcsókolta a homlokát, és visszaült a kanapéra. Elhallgattak.
- Szóval mondtam neked, Andre, légy kedves és nagylelkű, ahogy mindig is voltál. Ne ítélje meg Lise-t keményen – kezdte. - Olyan édes, olyan kedves, és most nagyon nehéz a helyzete.
- Úgy tűnik, hogy nem mondtam neked semmit, Mása, úgyhogy szemrehányást teszek a feleségemnek bármiért, vagy elégedetlen vagyok vele. Miért mondod el mindezt?
Mary hercegnő foltokban elpirult, és elhallgatott, mintha bűnösnek érezné magát.
„Nem mondtam neked semmit, de már mondták. És szomorúvá tesz.
A vörös foltok még erősebben jelentek meg Marya hercegnő homlokán, nyakán és arcán. Mondani akart valamit, de nem tudta kimondani. A testvér jól sejtette: a kis hercegnő vacsora után sírt, azt mondta, hogy előre látta a szerencsétlen születést, fél tőlük, panaszkodott a sorsára, az apósára és a férjére. Sírás után elaludt. Andrej herceg sajnálta a húgát.
- Tudj meg egyet, Mása, nem tehetek szemrehányást, nem tettem és soha nem is fogok szemrehányást tenni a feleségemnek, és magam sem tehetek szemrehányást vele kapcsolatban; és ez mindig így lesz, bármilyen körülmények között is leszek. De ha tudni akarod az igazságot... szeretnéd tudni, hogy boldog vagyok-e? Nem. Ő boldog? Nem. Miért ez? nem tudom…
Ezt mondva felállt, odament a nővéréhez, és lehajolva homlokon csókolta. Gyönyörű szemei intelligens és kedves, szokatlan ragyogással ragyogtak, de nem a nővérére nézett, hanem a nyitott ajtó sötétjébe, a fején keresztül.
- Menjünk hozzá, el kell búcsúznunk. Vagy menj egyedül, ébreszd fel, és azonnal jövök. Petrezselyem! kiáltott az inasnak: „Gyere ide, takaríts ki”. Az ülésben van, a jobb oldalon van.
Marya hercegnő felkelt, és az ajtóhoz ment. Megállt.
Andre, si vous avez. la foi, vous vous seriez adresse a Dieu, pour qu "il vous donne l" amour, que vous ne sentez pas et votre priere aurait ete exaucee. [Ha lenne hited, egy imával fordulnál Istenhez, hogy olyan szeretetet adjon neked, amit nem érzel, és meghallgatásra talál az imád.]
- Igen, az! - mondta András herceg. - Menj, Mása, mindjárt jövök.
Útban a nővére szobája felé, az egyik házat a másikkal összekötő galériában Andrej herceg találkozott egy kedvesen mosolygó m lle Bourienne-nel, aki aznap harmadszor bukkant rá lelkes és naiv mosollyal magányos járatokban.
- Ah! je vous croyais chez vous, [Á, azt hittem, a szobádban vagy] – mondta valamiért elpirulva, és lesütötte a szemét.
Andrej herceg szigorúan nézett rá. Andrej herceg arcán hirtelen harag jelent meg. Nem szólt hozzá semmit, csak a homlokát és a haját nézte, anélkül, hogy a szemébe nézett volna, olyan megvetően, hogy a francia nő elpirult, és szó nélkül távozott.
Amikor nővére szobája felé közeledett, a hercegnő már ébren volt, és a nyitott ajtóból kihallatszott az egyik szót a másik után siető vidám hangja. Úgy beszélt, mintha hosszú önmegtartóztatás után pótolni akarná az elvesztegetett időt.
- Non, mais figurez vous, la vieille comtesse Zouboff avec de fausses boucles et la bouche pleine de fausses dents, comme si elle voulait defier les annees ... [Nem, képzeld, öreg Zubova grófnő, hamis fürtökkel, hamis fogakkal, mintha kigúnyolná az éveket…] Xa, xa, xa, Marieie!
Pontosan ugyanezt a mondatot Zubova grófnőről és ugyanazt a nevetést Andrej herceg már ötször hallotta idegenek előtt a feleségétől.
Csendesen belépett a szobába. A gömbölyded, pirospozsgás hercegnő munkával a kezében egy karosszékben ült, és szüntelenül beszélt, válogatva a pétervári emlékek, sőt kifejezések között. Andrej herceg odajött, megsimogatta a fejét, és megkérdezte, kipihente-e az utazást. A lány válaszolt, és folytatta a beszélgetést.
A babakocsi hatban állt a bejáratnál. Sötét őszi éjszaka volt odakint. A kocsis nem látta a kocsi vonórúdját. Lámpás emberek nyüzsögtek a verandán. A hatalmas ház nagy ablakain keresztül égett a fény. A teremben tolongtak az udvarok, akik el akartak búcsúzni az ifjú hercegtől; az egész ház ott állt az előszobában: Mihail Ivanovics, Bourienne úr, Mária hercegnő és a hercegnő.
Andrej herceget apja irodájába hívták, aki négyszemközt szeretett volna elbúcsúzni tőle. Mindenki arra várt, hogy kijöjjenek.
Amikor Andrej herceg belépett az irodába, az öreg herceg öregszemüvegben és fehér köpenyében, amelyben a fián kívül senkit sem fogadott, az asztalnál ült és írt. Hátranézett.
- Mész? És újra írni kezdett.
- Elköszönni jöttem.
- Csók ide, - mutatta az arcát, - köszönöm, köszönöm!
- Mit köszönsz meg?
- Mert nem maradsz túl, nem ragaszkodsz a női szoknyához. Első a szolgáltatás. Köszönöm, köszönöm! És folytatta az írást, úgyhogy a recsegő tollból kiszállt a permet. - Ha mondanod kell valamit, mondd. Ezt a két dolgot meg tudom csinálni együtt” – tette hozzá.
– A feleségemről… nagyon szégyellem, hogy a karjaidban hagyom…
- Mit hazudsz? Mondja, amire szüksége van.
- Ha a feleségének lesz ideje szülni, küldjön Moszkvába szülészorvosért... Hogy itt legyen.
Az öreg herceg megállt, és mintha nem értené, szigorú szemekkel meredt fiára.
„Tudom, hogy senki sem tud segíteni, ha a természet nem segít” – mondta Andrej herceg láthatóan zavartan. „Egyetértek azzal, hogy millió esetből egy szerencsétlen, de ez az ő fantáziája és az enyém. Azt mondták neki, álmában látta, és fél.
„Hm… hm…” – mondta magában az öreg herceg, és folytatta az írást. - Fogok.
Áthúzta az aláírást, hirtelen gyorsan a fiához fordult és felnevetett.
- Rossz, nem?
- Mi a baj, apám?
- Feleség! – mondta röviden és jelentőségteljesen az öreg herceg.
– Nem értem – mondta Andrej herceg.
- Igen, nincs mit tenni, barátom - mondta a herceg -, mind ilyenek, nem fogsz férjhez menni. Ne félj; Nem mondom el senkinek; és te magad is tudod.
Csontos kis kezével megragadta a kezét, megrázta, gyors szemeivel egyenesen fia arcába nézett, amely mintha átlátott volna a férfin, és ismét felnevetett a hideg kacagásán.
A fiú felsóhajtott, és ezzel a sóhajjal bevallotta, hogy apja megértette őt. Az öreg folytatta a betűk hajtogatását és nyomtatását, szokásos gyorsaságával pecsétviaszt, pecsétet és papírt fogott és dobott.
- Mit kell tenni? Gyönyörű! mindent megteszek. Légy nyugodt – mondta ridegen gépelés közben.
Andrey hallgatott: kellemes és kellemetlen volt számára, hogy az apja megértette őt. Az öreg felkelt, és átadta a levelet a fiának.
– Figyelj – mondta –, ne aggódj a felesége miatt: amit meg lehet tenni, az meg lesz. Most figyelj: add át a levelet Mihail Ilarionovicsnak. Azt írom, hogy jó helyekre fogja használni, és nem tart sokáig adjutánsként: rossz pozíció! Mondd meg neki, hogy emlékszem rá és szeretem. Igen, írd meg, hogyan fogad el. Ha jó, tálaljuk. Nyikolaj Andrej Bolkonszkij fia könyörületből senkit sem fog szolgálni. Na, most gyere ide.
Olyan gyorsan beszélt, hogy a felét sem fejezte be, de a fiú hozzászokott, hogy megértse. A fiát az irodához vezette, ledobta a fedelet, kihúzott egy fiókot, és elővett egy nagy, hosszú, tömör kézírással borított füzetet.
– Előtted kell meghalnom. Tudd meg, hogy itt vannak a jegyzeteim, hogy halálom után átadjam őket az uralkodónak. Most itt - itt egy zálogjegy és egy levél: ez a jutalom annak, aki a Szuvorov-háborúk történetét írja. Jelentkezzen be az akadémiára. Íme a megjegyzéseim, miután elolvastam magad, találsz valami hasznosat.
Andrej nem mondta el apjának, hogy valószínűleg sokáig fog élni. Tudta, hogy nem kell kimondania.
– Mindent megteszek, apám – mondta.
- Na, most viszont viszlát! Hagyta, hogy fia kezet csókoljon, és megölelte. „Emlékezz egy dologra, Andrej herceg: ha megölnek, az az öregnek fájni fog…” Hirtelen elhallgatott, és hirtelen hangosan folytatta: „És ha megtudom, hogy nem úgy viselkedtél, mint a fia. Nyikolaj Bolkonszkij,... szégyellni fogom! – rikoltotta.
– Ezt nem mondhattad el nekem, apám – mondta a fiú mosolyogva.
Az öreg hallgatott.
- Azt is meg akartam kérdezni - folytatta Andrej herceg -, ha megölnek, és ha fiam lesz, ne hagyd, hogy elmenjen tőled, ahogy tegnap mondtam, hogy veled nőjön fel... kérem.
- Ne add oda a feleségednek? – mondta az öreg és nevetett.
Némán álltak egymással szemben. Az öregember gyors tekintete egyenesen a fia szemére szegeződött. Valami megremegett az öreg herceg arcának alsó részén.
- Viszlát... menj! – mondta hirtelen. - Felkelni! – kiáltotta dühösen és hangosan, és kinyitotta az iroda ajtaját.
- Mi az, mi? - kérdezte a hercegnő és a hercegnő, látva Andrej herceget és egy pillanatra egy idős férfi alakját, fehér köpenyben, paróka nélkül, öregszemüvegben, kihajolva dühös hangon.
Andrej herceg felsóhajtott, és nem válaszolt.
– Nos – mondta a feleségéhez fordulva.
És ez a „kút” hideg gúnynak tűnt, mintha azt mondaná: „most csináld a trükkjeidet”.
Andre, deja! [Andrey, már!] - mondta a kis hercegnő elsápadva, és félve nézett férjére.
Megölelte. Felsikoltott, és eszméletlenül a férfi vállára esett.
Finoman hátrahúzta a vállát, amelyen a lány feküdt, az arcába nézett, és óvatosan leültette egy székre.
- Viszlát, Marieie, [Viszlát, Mása,] - mondta halkan a húgának, kézen fogva megcsókolta és gyorsan kiment a szobából.
A hercegnő egy karosszékben feküdt, m lle Bourienne a halántékát dörzsölte. Mária hercegnő menyét támogatva, könnyes szép szemekkel még mindig az ajtót nézte, amelyen Andrej herceg kiment, és megkeresztelte. A dolgozószobából lövésekként hallatszottak az öreg orrfújó, dühös hangjai. Amint Andrej herceg elment, gyorsan kinyílt az iroda ajtaja, és egy szigorú, fehér köpenyes öregember nézett ki rajta.
- Bal? Hát jó! - mondta dühösen az érzéketlen kis hercegnőre nézve, szemrehányóan megrázta a fejét, és becsapta az ajtót.

1805 októberében az orosz csapatok elfoglalták az Osztrák Főhercegség falvait és városait, és újabb új ezredek érkeztek Oroszországból, és a lakosokat a braunaui erőd közelében helyezték el. Braunauban volt Kutuzov főparancsnok fő lakása.
1805. október 11-én fél mérföldre állt a várostól az egyik gyalogezred, amely éppen Braunauba érkezett, és várta a főparancsnok felülvizsgálatát. A nem orosz terep és helyzet ellenére (gyümölcsöskertek, kőkerítések, cseréptetők, távolban látható hegyek), a katonákra kíváncsian pillantó nem oroszok, az ezred pontosan olyan volt, mint bármelyik készülő orosz ezred. egy előadásra valahol Oroszország közepén.

Egy konvergens numerikus sorozat határának és korlátjának egyedisége

1. definíció . Egy numerikus sorozatot (1) korlátosnak nevezünk, ha a sorozat tagjainak halmaza korlátos halmazt alkot.

Ebben az esetben a numerikus sorozatot (1) hívjuk. korlátozott érték.

2. definíció . A numerikus sorozat (1) konvergál és van határa (Lehetséges a jelölés használata), ha .

Ismételjük meg ezt a meghatározást, az orosz nyelvet használva. Egy numerikus sorozat határértéke létezik és egyenlő valamilyen számmal, ha valamely számból kiindulva a sorozat összes tagja kikerül ebből limit szám kisebb, mint bármely előre meghatározott, tetszőleges kis pozitív szám. Ugyanez más szavakkal is elmondható. A szám akkor és csak akkor lesz az (1) numerikus sorozat határa, ha a pont minden -szomszédságára a sorozat minden tagja, valamilyen számból kiindulva, ebben a -körzetben található. Vegye figyelembe, hogy az intervallumot a pont -szomszédságának nevezik.

1. tétel . Ha egy numerikus sorozat határértéke létezik, akkor az egyedi.

Bizonyíték . Bizonyítsuk be a tételt az "ellentmondásos módszerrel". Tegyük fel, hogy a tétel hamis, és van legalább 2 olyan szám és () amelyekre teljesülnek a 2. definíció feltételei. Ebben a definícióban vesszük . Ekkor a szám után a sorozat tagjai kisebb mértékben térnek el a számtól, mint, a szám után pedig a sorozat tagjai kisebb mértékben térnek el a számtól, mint . Mutassuk meg, hogy ez nem lehet. Valójában at a , , kapcsolatok kielégülnek, honnan van ezekre . A tétel bizonyítást nyert.

2. tétel . Ha egy számsorozatnak van határa, akkor ez a számsorozat korlátos.

Bizonyíték . A bizonyítás építő jellegű lesz. Vegyük és keressük meg a megfelelőt. Osszuk fel a sorozatot 2 részre: a sorozat első és fennmaradó tagjaira. Az első csoport véges számú tagból áll, ezért korlátozott. A második csoportba azok a számok tartoznak, amelyek legfeljebb 1 távolságra vannak a határértéktől, ezért szintén korlátozottak. Két korlátos halmaz uniója korlátos halmaz. A tétel bizonyítást nyert.

Végtelenül kis mennyiségek és tulajdonságaik

3. definíció . A számsort hívják végtelenül kicsi ha 0-val egyenlő határértéke van.

A végtelenül kicsi mennyiségeknél a jelölést használjuk b. m.

Legyenek numerikus sorozatok és adottak. Egy közös tagú numerikus sorozatot ezek összegének nevezünk számsorozatok. A közös taggal rendelkező numerikus sorozatot e numerikus sorozatok összegének nevezzük. A közös taggal rendelkező numerikus sorozatot e numerikus sorozatok összegének nevezzük.

3. tétel . Véges számú végtelenül kicsi mennyiség összege végtelenül kicsi mennyiség.

Bizonyíték . Elég bizonyítani az állítást két b összegére. m. Legyenek a és numerikus sorozatok végtelenül kicsi mennyiségek, azaz ezeknek a sorozatoknak a határértékei egyenlők 0-val. Ezt a tényt a következőket jelenti. Ha egy tetszőlegesen görgetően kis pozitív számot adunk meg, akkor a számhoz és a numerikus sorozathoz létezik egy olyan szám, amelynek a tulajdonsága az, hogy . Ugyanebből az okból, ugyanannak a számnak és számsorozatnak, létezik olyan szám, amely rendelkezik azzal a tulajdonsággal, amelyre a reláció érvényes. Vegyünk egy számot , majd a . Tehát egy tetszőleges számra találtunk olyan számot, hogy mikor . Ezért a sorozat határértéke 0, és ez egy végtelenül kicsi mennyiség. A tétel bizonyítást nyert.

4. tétel . Egy végtelenül kicsi mennyiségnek egy korlátozott mennyiséggel való szorzata egy végtelenül kicsi mennyiség.

Bizonyíték . Legyen a numerikus sorozat egy végtelenül kicsi érték, a numerikus sorozat pedig egy korlátos érték. Ez azt jelenti, hogy egyrészt , másrészt van olyan szám, amelyre a feltétel mindegyikre teljesül. Most adjunk meg egy tetszőleges, görgetően kicsi pozitív számot. Tekintsük a számot, mert a numerikus sorozatban van egy szám, amelynek megvan az a tulajdonsága, amelyre a reláció érvényes. Ebben az esetben a feltétel , ami azt jelenti, hogy e két mennyiség – végtelenül kicsi és korlátozott – szorzata egy végtelenül kicsi mennyiség. A tétel bizonyítást nyert.

Limit Properties

És pontosan hogyan történik a határértékek számítása, jelen esetben a numerikus sorozatok? Az értéket, melynek határát meg kell találni, igyekszünk egyszerűbb mennyiségek összegeként, különbségeként, szorzataként, hányadosaként ábrázolni, aminek a határa könnyen megtalálható. Egy ilyen megközelítés igazolásához szükséges a határértékek tulajdonságainak megfogalmazása és bizonyítása.

5. tétel . Egy számsorozat határértéke akkor és csak akkor egyenlő, ha a sorozat végtelenül kicsi.

Bizonyíték . Legyen , azaz mindegyik esetén teljesül a () egyenlőtlenség. De ez az egyenlőtlenség egyenlő azzal Amellett, hogy , azaz a sorozatnak 0 a határértéke, azaz végtelenül kicsi mennyiség. A tétel bizonyítást nyert. , ahol - b. m. Ebből következik, hogy . Az utolsó zárójelben két végtelenül kicsi mennyiség összege a b mennyiség. m) Ezért összegként és végtelenül kicsi értékként ábrázoljuk. Az 5. Tétel értelmében ez azt jelenti . A tétel első állítása bizonyítást nyer. Képlet pontosan ugyanúgy bizonyított. Fontolja meg most a képletet és ugyanazt a jelölést használja a bal oldal átalakításához. Ezért …

Az infinitezimális sorozat definíciója adott. Konvergens sorozatok tulajdonságaival rendelkezik. Vannak olyan tulajdonságok is, amelyek csak a nullával egyenlő határértékkel rendelkező sorozatokra jellemzőek. Az ilyen tulajdonságok bizonyítékai vannak megadva. Egy olyan példát veszünk figyelembe, amelyben be kell bizonyítani, hogy a sorozat végtelenül kicsi.

Tartalom

Meghatározás

Infinitezimális sorozat (αn) egy konvergens sorozat, amelynek határértéke nulla:
.

A következő tulajdonságok egyenes következményei az aritmetikai tulajdonságoknak, amelyeket olyan sorozatokra alkalmaznak, amelyek határértéke nulla.

Infinitezimális sorozatok összegének és különbségének tulajdonsága

Összeg és különbség véges számú infinitezimális sorozat egy infinitezimális sorozat.
Is lineáris kombináció véges számú infinitezimális sorozat egy infinitezimális sorozat.
A numerikus sorozatok összegének és különbségének határának bizonyítása.

Infinitezimális sorozatok szorzattulajdonsága

Egy véges szám szorzata Az infinitezimális sorozatok egy infinitezimális sorozat.
A számsorozatok szorzatának határértékének bizonyítása.

A következő tulajdonságok csak infinitezimális sorozatokra vonatkoznak, és nem közvetlen következményei a konvergens sorozatok tulajdonságainak.

(x n)
x n \u003d b + α n,
ahol (αn)

Tulajdoni igazolások

Egy végtelen kicsivel határolt sorozat szorzatának tulajdonsága

Korlátozott sorozat szorzata infinitezimálishoz egy infinitezimális sorozat.

Bizonyíték

Korlátozzuk a sorozatot valamilyen számmal:
(3.1) .

Legyen a sorozat végtelenül kicsi. Vagyis van egy olyan függvény a változótól függően, hogy a változó bármely pozitív értékére az egyenlőtlenség
(3.2) nál nél .

Legyen a sorozat az és sorozatok szorzata. Általános kifejezése:
.
Olyan függvényt kell találnunk, amely kielégíti az egyenlőtlenséget
(3.3) nál nél .

Alkalmazzuk (3.1) és (3.2):
.
Ez a következővel történik. Így,
.
Tegyük fel:
.

Vagyis találtunk egy olyan függvényt, amely alatt bármely pozitív számra igaz a következő egyenlőtlenség:
(3.3) nál nél .

Az ingatlan bizonyított.

Az a tulajdonsága, hogy egy konvergens sorozatot infinitezimálisan ábrázolunk

A sorrend érdekében (x n) b határértéke van, szükséges és elégséges, hogy
x n \u003d b + α n,
ahol (αn) egy végtelenül kicsi sorozat.

Bizonyíték

Szükség. Hadd . Tekintsünk egy sorozatot egy közös kifejezéssel. A határértékek aritmetikai tulajdonságait használjuk:
.
Vagyis egy végtelenül kicsi sorozat.

Megfelelőség. Hadd . A határértékek aritmetikai tulajdonságai alapján a következőket kapjuk:
.

Az ingatlan bizonyított.

Példa

Minden példa Egy sorozat határértékének definíciójával igazolja, hogy a sorozat

végtelenül kicsi.

Felírjuk egy infinitezimális sorozat definícióját:
.
Mivel n természetes szám, n = 1, 2, 3, ... , akkor
,
,
.
Ezért a sorozat tagjai pozitív számok. Akkor
.

Tehát a következő pontszámot kaptuk:
.
Belép pozitív számokés:
.
Az egyenlőtlenségek tulajdonságai szerint, ha és , akkor
.

Ebből következik, hogy minden pozitívat megtalálhat természetes szám, tehát at ,
.
Ez azt jelenti, hogy az eredeti sorozat határértéke nulla, és ezért végtelenül kicsi.

VÉGTELEN KIS FUNKCIÓK ÉS FŐ TULAJDONSÁGAIK

Funkció y=f(x) hívott elenyésző nál nél x→a vagy mikor x→∞ ha vagy , azaz. Az infinitezimális függvény olyan függvény, amelynek határértéke egy adott pontban nulla.

Példák.

Állítsuk fel a következő fontos összefüggést:

Tétel. Ha a funkció y=f(x) képviselhető at x→aállandó szám összegeként bés végtelenül kicsi α(x): f(x)=b+ α(x) akkor .

Fordítva, ha , akkor f(x)=b+α(x), ahol fejsze) végtelenül kicsi a x→a.

Bizonyíték.

Tekintsük az infinitezimális függvények főbb tulajdonságait.

1. tétel. Kettő, három és általában tetszőleges számú infinitezimális algebrai összege végtelen kicsi függvény.

Bizonyíték. Bizonyítsunk két kifejezésre. Hadd f(x)=α(x)+β(x), hol és . Be kell bizonyítanunk, hogy tetszőleges tetszőlegesen kicsi ε esetén > 0 ott δ> 0, olyan, hogy x az egyenlőtlenség kielégítése |x – a|<δ , előadták |f(x)|< ε.

Szóval javítsuk ki tetszőleges szám ε > 0. Mivel a tétel hipotézise szerint α(x) egy infinitezimális függvény, akkor létezik δ 1 > 0, amely at |x – a|< δ 1 van |α(x)|< ε / 2. Ugyanígy, mióta β(x) végtelenül kicsi, akkor van ilyen δ 2 > 0, amely at |x – a|< δ 2 van | β(x)|< ε / 2.

Vessünk δ=min(δ1 , δ2 } .Akkor a pont szomszédságában a sugár δ mindegyik egyenlőtlenség teljesülni fog |α(x)|< ε / 2 és | β(x)|< ε / 2. Ezért ezen a környéken lesz

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,

azok. |f(x)|< ε, amit bizonyítani kellett.

2. tétel. Egy infinitezimális függvény szorzata fejsze) korlátozott funkcióhoz f(x) nál nél x→a(vagy mikor x→∞) egy infinitezimális függvény.

Bizonyíték. Mivel a funkció f(x) korlátozott, akkor van egy szám M olyan, hogy minden értékre x a pont valamelyik környékéről a|f(x)|≤M. Ráadásul mivel fejsze) egy végtelenül kicsi függvény x→a, akkor tetszőleges ε-re > 0 van a pont szomszédsága a, amelyben az egyenlőtlenség |α(x)|< ε /M. Aztán a kisebbik környéken van | αf|< ε /M= ε. Ez pedig azt jelenti af- végtelenül kicsi. Az esethez x→∞ a bizonyítás is hasonló módon történik.

A bizonyított tételből az következik:

Következmény 1. Ha és , akkor .

2. következmény. Ha és c= const, akkor .

3. tétel. Egy infinitezimális függvény aránya α(x) függvényenként f(x), amelynek határértéke nem nulla, egy infinitezimális függvény.

Bizonyíték. Hadd . Aztán 1 /f(x) van korlátozott funkció. Ezért a tört egy infinitezimális függvény és egy korlátos függvény szorzata, azaz. függvény végtelenül kicsi.

VÉGTELEN KIS ÉS VÉGTELEN NAGY FUNKCIÓK KAPCSOLATA

1. tétel. Ha a funkció f(x) végtelenül nagy at x→a, majd az 1. függvény /f(x) végtelenül kicsi a x→a.

Bizonyíték. Vegyünk egy tetszőleges ε számot >0 és ezt mutasd meg egyeseknek δ>0 (ε-től függően) mindenre x, amelyekre |x – a|<δ , az egyenlőtlenség teljesül, és ez azt fogja jelenteni 1/f(x) egy végtelenül kicsi függvény. Valóban, azóta f(x) egy végtelenül nagy függvény a x→a, akkor van δ>0 olyan, hogy amint |x – a|<δ , tehát | f(x)|> 1/ ε. De akkor ugyanerre x.

Példák.

A fordított tétel is igazolható.

2. tétel. Ha a funkció f(x)- végtelenül kicsi at x→a(vagy x→∞)és akkor nem tűnik el y= 1/f(x) egy végtelen függvény.

Te magad bizonyítsd be a tételt.

Példák.

Így a végtelenül kicsi és végtelenül nagy függvények legegyszerűbb tulajdonságai a következő feltételes összefüggésekkel írhatók fel: A≠ 0

TÉTELEK A HATÁROKRÓL

1. tétel. Két, három és általában bizonyos számú függvény algebrai összegének határa megegyezik e függvények határainak algebrai összegével, azaz.

Bizonyíték. A bizonyítást két tagra hajtjuk végre, mivel tetszőleges számú tagra ugyanúgy történik. Hadd .Akkor f(x)=b+α(x)és g(x)=c+β(x), ahol α és β végtelenül kicsi függvények. Következésképpen,

f(x) + g(x)=(b + c) + (α(x) + β(x)).

Mert b+c egy állandó, és α(x) + β(x) akkor egy végtelenül kicsi függvény

Példa. .

2. tétel. Két, három és általában véges számú függvény szorzatának határa egyenlő ezen függvények határértékeinek szorzatával:

Bizonyíték. Hadd . Következésképpen, f(x)=b+α(x)és g(x)=c+β(x)és

fg = (b + α) (c + β) = bc + (bβ + cα + αβ).

Munka időszámításunk előttállandó érték. Funkció bβ + cα + αβ az infinitezimális függvények tulajdonságai alapján van egy végtelenül kicsi mennyiség. Ezért .

Következmény 1. A konstans tényező kivehető a határjelből:

2. következmény. A fokozat határa megegyezik a határ fokával:

Példa..

3. tétel. Két függvény hányadosának határa egyenlő e függvények határértékeinek hányadosával, ha a nevező határértéke eltér nullától, azaz.

Bizonyíték. Hadd . Következésképpen, f(x)=b+α(x)és g(x)=c+β(x), ahol α, β végtelenül kicsik. Tekintsük a hányadost

A tört egy végtelenül kicsi függvény, mert a számláló egy végtelenül kicsi függvény, és a nevezőnek van határa c2 ≠0.

Példák.

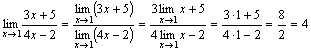
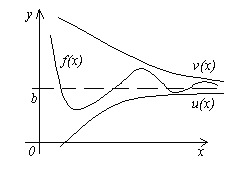
4. tétel. Legyen három függvény adott f(x), u(x)és v(x), az egyenlőtlenségek kielégítése u (x)≤f(x)≤v(x). Ha funkciókat u(x)és v(x) ugyanaz a határ x→a(vagy x→∞), majd a függvényt f(x) ugyanarra a határra hajlik, i.e. ha

, akkor .

Ennek a tételnek a jelentése világos az ábrából.

A 4. tétel bizonyítása megtalálható például a tankönyvben: Piskunov N. S. Differenciál- és integrálszámítás, 1. kötet - M .: Nauka, 1985.

5. tétel.Én Kövér x→a(vagy x→∞) funkciót y=f(x) nem negatív értékeket vesz fel y≥0és a határig hajlik b, akkor ez a határ nem lehet negatív: b≥0.

Bizonyíték. A bizonyítás ellentmondással történik. Tegyünk úgy, mintha b<0 , akkor |y – b|≥|b|és ezért a különbség modulusa nem nullázódik at x→a. De aztán y nem megy a határig b nál nél x→a, ami ellentmond a tétel feltételének.

6. tétel. Ha két funkciót f(x)és g(x) az érv összes értékére x kielégíti az egyenlőtlenséget f(x)≥ g(x)és vannak határai, akkor megvan az egyenlőtlenség b≥c.

Bizonyíték. A tétel szerint f(x)-g(x) ≥0 tehát az 5. Tétel szerint , vagy .

EGYOLDALAS HATÁROK

Eddig egy függvény határának meghatározását vettük figyelembe, amikor x→aönkényesen, azaz. a függvény határa nem attól függött, hogy a x felé a, balra vagy jobbra a. Azonban meglehetősen gyakori, hogy olyan függvényeket találunk, amelyeknek nincs korlátja ebben a feltételben, de van korlátjuk, ha x→a, az egyik oldalon maradva a, balra vagy jobbra (lásd az ábrát). Ezért bevezetik az egyoldalú korlátok fogalmát.

Ha egy f(x) a határig hajlik b nál nél x valamilyen számra törekedve aígy x csak kisebb értékeket vesz fel a, majd írj és hívj az f(x) függvény határértéke a bal oldali a pontban.