VÉGTELEN KIS FUNKCIÓK ÉS FŐ TULAJDONSÁGAIK

Funkció y=f(x) hívott elenyésző nál nél x→a vagy mikor x→∞ ha vagy , azaz. Az infinitezimális függvény olyan függvény, amelynek határértéke egy adott pontban nulla.

Példák.

Állítsuk fel a következő fontos összefüggést:

Tétel. Ha a funkció y=f(x) képviselhető at x→aállandó szám összegeként bés végtelenül kicsi α(x): f(x)=b+ α(x) akkor .

Fordítva, ha , akkor f(x)=b+α(x), ahol fejsze) végtelenül kicsi a x→a.

Bizonyíték.

Tekintsük az infinitezimális függvények főbb tulajdonságait.

1. tétel. Kettő, három és általában tetszőleges számú infinitezimális algebrai összege végtelen kicsi függvény.

Bizonyíték. Bizonyítsunk két kifejezésre. Hadd f(x)=α(x)+β(x), hol és . Be kell bizonyítanunk, hogy tetszőleges tetszőlegesen kicsi ε esetén > 0 ott δ> 0, olyan, hogy x az egyenlőtlenség kielégítése |x – a|<δ , előadták |f(x)|< ε.

Szóval javítsuk ki tetszőleges szám ε > 0. Mivel a tétel hipotézise szerint α(x) egy infinitezimális függvény, akkor létezik δ 1 > 0, amely at |x – a|< δ 1 van |α(x)|< ε / 2. Ugyanígy, mivel β(x) végtelenül kicsi, akkor van ilyen δ 2 > 0, amely at |x – a|< δ 2 van | β(x)|< ε / 2.

Vessünk δ=min(δ1 , δ2 } .Akkor a pont szomszédságában a sugár δ mindegyik egyenlőtlenség teljesülni fog |α(x)|< ε / 2 és | β(x)|< ε / 2. Ezért ezen a környéken lesz

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,

azok. |f(x)|< ε, amit bizonyítani kellett.

2. tétel. A munka végtelen kis funkció fejsze) korlátozott funkcióhoz f(x) nál nél x→a(vagy mikor x→∞) egy infinitezimális függvény.

Bizonyíték. Mivel a funkció f(x) korlátozott, akkor van egy szám M olyan, hogy minden értékre x a pont valamelyik környékéről a|f(x)|≤M. Ráadásul mivel fejsze) egy végtelenül kicsi függvény x→a, akkor tetszőleges ε-re > 0 van a pont szomszédsága a, amelyben az egyenlőtlenség |α(x)|< ε /M. Aztán a kisebbik környéken van | αf|< ε /M= ε. Ez pedig azt jelenti af- végtelenül kicsi. Az esethez x→∞ a bizonyítás is hasonló módon történik.

A bizonyított tételből az következik:

Következmény 1. Ha és , akkor .

2. következmény. Ha és c= const, akkor .

3. tétel. Egy infinitezimális függvény aránya α(x) függvényenként f(x), amelynek határértéke nem nulla, egy infinitezimális függvény.

Bizonyíték. Hadd . Aztán 1 /f(x) korlátozott funkciója van. Ezért a tört egy infinitezimális függvény és egy korlátos függvény szorzata, azaz. függvény végtelenül kicsi.

VÉGTELEN KIS ÉS VÉGTELEN NAGY FUNKCIÓK KAPCSOLATA

1. tétel. Ha a funkció f(x) végtelenül nagy at x→a, majd az 1. függvény /f(x) végtelenül kicsi a x→a.

Bizonyíték. Vegyünk egy tetszőleges ε számot >0 és ezt mutasd meg egyeseknek δ>0 (ε-től függően) mindenre x, amelyekre |x – a|<δ , az egyenlőtlenség teljesül, és ez azt fogja jelenteni 1/f(x) egy végtelenül kicsi függvény. Valóban, azóta f(x) egy végtelenül nagy függvény a x→a, akkor van δ>0 olyan, hogy amint |x – a|<δ , tehát | f(x)|> 1/ ε. De akkor ugyanerre x.

Példák.

A fordított tétel is igazolható.

2. tétel. Ha a funkció f(x)- végtelenül kicsi at x→a(vagy x→∞)és akkor nem tűnik el y= 1/f(x) egy végtelen függvény.

Te magad bizonyítsd be a tételt.

Példák.

Így a végtelenül kicsi és végtelenül nagy függvények legegyszerűbb tulajdonságai a következő feltételes összefüggésekkel írhatók fel: A≠ 0

TÉTELEK A HATÁROKRÓL

1. tétel. Két, három és általában bizonyos számú függvény algebrai összegének határa megegyezik e függvények határainak algebrai összegével, azaz.

Bizonyíték. A bizonyítást két tagra hajtjuk végre, mivel tetszőleges számú tagra ugyanúgy történik. Hadd .Akkor f(x)=b+α(x)és g(x)=c+β(x), ahol α és β végtelenül kicsi függvények. Következésképpen,

f(x) + g(x)=(b + c) + (α(x) + β(x)).

Mert b+c egy állandó, és α(x) + β(x) akkor egy végtelenül kicsi függvény

Példa. .

2. tétel. Két, három és általában véges számú függvény szorzatának határa egyenlő ezen függvények határértékeinek szorzatával:

Bizonyíték. Hadd . Következésképpen, f(x)=b+α(x)és g(x)=c+β(x)és

fg = (b + α) (c + β) = bc + (bβ + cα + αβ).

Munka időszámításunk előttállandó érték. Funkció bβ + cα + αβ az infinitezimális függvények tulajdonságai alapján van egy végtelenül kicsi mennyiség. Ezért .

Következmény 1. A konstans tényező kivehető a határjelből:

.

2. következmény. A fokozat határa megegyezik a határ fokával:

.

Példa..

3. tétel. Két függvény hányadosának határa egyenlő e függvények határértékeinek hányadosával, ha a nevező határa nullától eltérő, azaz.

.

Bizonyíték. Hadd . Következésképpen, f(x)=b+α(x)és g(x)=c+β(x), ahol α, β végtelenül kicsik. Tekintsük a hányadost

A tört egy végtelenül kicsi függvény, mert a számláló egy végtelenül kicsi függvény, és a nevezőnek van határa c2 ≠0.

Példák.

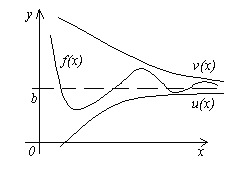
4. tétel. Legyen három függvény adott f(x), u(x)és v(x), az egyenlőtlenségek kielégítése u (x)≤f(x)≤v(x). Ha funkciókat u(x)és v(x) ugyanaz a határ x→a(vagy x→∞), majd a függvényt f(x) ugyanarra a határra hajlik, i.e. ha

, akkor .

Ennek a tételnek a jelentése világos az ábrából.

A 4. tétel bizonyítása megtalálható például a tankönyvben: Piskunov N. S. Differenciál- és integrálszámítás, 1. kötet - M .: Nauka, 1985.

5. tétel.Én Kövér x→a(vagy x→∞) funkciót y=f(x) nem negatív értékeket vesz fel y≥0és a határig hajlik b, akkor ez a határ nem lehet negatív: b≥0.

Bizonyíték. A bizonyítás ellentmondással történik. Tegyünk úgy, mintha b<0 , akkor |y – b|≥|b|és ezért a különbség modulusa nem nullázódik at x→a. De aztán y nem megy a határig b nál nél x→a, ami ellentmond a tétel feltételének.

6. tétel. Ha két funkciót f(x)és g(x) az érv összes értékére x kielégíti az egyenlőtlenséget f(x)≥ g(x)és vannak határai, akkor megvan az egyenlőtlenség b≥c.

Bizonyíték. A tétel szerint f(x)-g(x) ≥0 tehát az 5. Tétel szerint , vagy .

EGYOLDALAS HATÁROK

Eddig egy függvény határának meghatározását vettük figyelembe, amikor x→aönkényesen, azaz. a függvény határa nem attól függött, hogy a x felé a, balra vagy jobbra a. Azonban meglehetősen gyakori, hogy olyan függvényeket találunk, amelyeknek nincs korlátja ebben a feltételben, de van korlátjuk, ha x→a, az egyik oldalán maradva a, balra vagy jobbra (lásd az ábrát). Ezért bevezetik az egyoldalú korlátok fogalmát.

Ha egy f(x) a határig hajlik b nál nél x valamilyen számra törekedve aígy x csak kisebb értékeket vesz fel a, majd írj és hívj az f(x) függvény határértéke a bal oldali a pontban.

Funkció y=f(x) hívott elenyésző nál nél x→a vagy mikor x→∞ ha vagy , azaz. Az infinitezimális függvény olyan függvény, amelynek határértéke egy adott pontban nulla.

Példák.

1. Funkció f(x)=(x-1) 2 végtelenül kicsi x→1, mivel (lásd ábra).

2. Funkció f(x)=tg x végtelenül kicsi a x→0.

3. f(x)= log(1+ x) végtelenül kicsi a x→0.

4. f(x) = 1/x végtelenül kicsi a x→∞.

Állítsuk fel a következő fontos összefüggést:

Tétel. Ha a funkció y=f(x) képviselhető at x→aállandó szám összegeként bés végtelenül kicsi α(x): f(x)=b+ α(x) akkor .

Fordítva, ha , akkor f(x)=b+α(x), ahol fejsze) végtelenül kicsi a x→a.

Bizonyíték.

1. Bizonyítsuk be az állítás első részét. Az egyenlőségtől f(x)=b+α(x) kellene |f(x) – b|=| α|. De azóta fejsze) infinitezimális, akkor tetszőleges ε esetén van δ, a pont szomszédsága a, mindenkinek x ahonnan, értékek fejsze) kielégíti a kapcsolatot |α(x)|< ε. Akkor |f(x) – b|< ε. Ez pedig azt jelenti, hogy.

2. Ha , akkor bármely ε esetén >0 mindenkinek x valamilyen δ a pont szomszédsága a lesz |f(x) – b|< ε. De ha jelöljük f(x) – b= α, akkor |α(x)|< ε, ami azt jelenti a- végtelenül kicsi.

Tekintsük az infinitezimális függvények főbb tulajdonságait.

1. tétel. Kettő, három és általában tetszőleges számú infinitezimális algebrai összege végtelen kicsi függvény.

Bizonyíték. Bizonyítsunk két kifejezésre. Hadd f(x)=α(x)+β(x), hol és . Be kell bizonyítanunk, hogy tetszőleges tetszőlegesen kicsi ε esetén > 0 ott δ> 0, olyan, hogy x az egyenlőtlenség kielégítése |x – a|<δ , előadták |f(x)|< ε.

Így egy tetszőleges ε számot rögzítünk > 0. Mivel a tétel hipotézise szerint α(x) egy infinitezimális függvény, akkor létezik δ 1 > 0, amely at |x – a|< δ 1 van |α(x)|< ε / 2. Ugyanígy, mivel β(x) végtelenül kicsi, akkor van ilyen δ 2 > 0, amely at |x – a|< δ 2 van | β(x)|< ε / 2.

Vessünk δ=min(δ1 , δ2 } .Akkor a pont szomszédságában a sugár δ mindegyik egyenlőtlenség teljesülni fog |α(x)|< ε / 2 és | β(x)|< ε / 2. Ezért ezen a környéken lesz

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,

azok. |f(x)|< ε, amit bizonyítani kellett.

2. tétel. Egy infinitezimális függvény szorzata fejsze) korlátozott funkcióhoz f(x) nál nél x→a(vagy mikor x→∞) egy infinitezimális függvény.

Bizonyíték. Mivel a funkció f(x) korlátozott, akkor van egy szám M olyan, hogy minden értékre x a pont valamelyik környékéről a|f(x)|≤M. Ráadásul mivel fejsze) egy végtelenül kicsi függvény x→a, akkor tetszőleges ε-re > 0 van a pont szomszédsága a, amelyben az egyenlőtlenség |α(x)|< ε /M. Aztán a kisebbik környéken van | αf|< ε /M= ε. Ez pedig azt jelenti af- végtelenül kicsi. Az esethez x→∞ a bizonyítás is hasonló módon történik.

A bizonyított tételből az következik:

Következmény 1. Ha és , akkor .

2. következmény. Ha és c= const, akkor .

3. tétel. Egy infinitezimális függvény aránya α(x) függvényenként f(x), amelynek határértéke nem nulla, egy infinitezimális függvény.

Bizonyíték. Hadd . Aztán 1 /f(x) korlátozott funkciója van. Ezért a tört egy infinitezimális függvény és egy korlátos függvény szorzata, azaz. függvény végtelenül kicsi.

Meghatározás numerikus függvény. A funkciók beállításának módjai.

Legyen D egy halmaz az R valós egyenesen. Ha minden D-hez tartozó x-hez egyetlen y=f(x) szám tartozik, akkor azt mondjuk, hogy adott az f függvény.

A funkciók beállításának módjai:

1) táblázatos - véges halmazon definiált függvényekhez.

2) elemző

3) grafika

2 és 3 - a végtelen halmazon meghatározott függvényekhez.

Az inverz függvény fogalma.

Ha az y=f(x) függvény olyan, hogy az x argumentum különböző értékei megfelelnek különböző jelentések függvényt, akkor az x változó az y változó függvényeként fejezhető ki: x=g(y). A g függvényt f inverzének nevezzük, és f^(-1) jelöli.

A komplex függvény fogalma.

Összetett függvény - funkció, amelynek argumentuma bármely más függvény.

Legyen adott f(x) és g(x) függvény. Készítsünk belőlük két összetett függvényt. Ha az f függvényt külsőnek (fő) és a g függvényt belsőnek tekintjük, azt kapjuk összetett funkció u(x)=f(g(x)).

Sorozat határának meghatározása.

Az a számot a sorozat (xn) határértékének nevezzük, ha bármely pozitív számhoz létezik n0 szám, amelyből kiindulva az utolsónak minden tagja in modulo kisebb, mint ε (azaz beleesik az ε-be). az a pont szomszédsága):

A konvergens sorozatok határértékeinek kiszámításának szabályai.

1. Minden konvergens sorozatnak csak egy határa van. 2. Ha az (x n) sorozat minden eleme egyenlő C-vel (állandó), akkor az (x n) sorozat határértéke is egyenlő C-vel. 3. ; 4. ; 5. .

Korlátozott sorozat definíciója.

Az (x n ) sorozatot korlátozottnak nevezzük, ha az X=(x n ) számkészlet korlátozott: .

Infinitezimális sorozat definíciója.

Az (x n ) sorozatot infinitezimálisnak nevezzük, ha bármely (tetszőlegesen kicsi) >0 esetén van olyan n 0 szám, hogy bármely n>n 0 esetén az |x n |< .

Egy végtelenül nagy sorozat definíciója.

A sorozatot végtelenül nagynak nevezzük, ha bármely (tetszőlegesen nagy) A>0 számra van olyan n 0 szám, hogy bármely n>n 0 számra teljesül az |x n |> A egyenlőtlenség.

Monoton sorozatok meghatározása.

Monoton sorozatok: 1) növekszik, ha x n x n +1 minden n-re, 4) nem növekvő, ha x n x n +1 minden n-re.

Egy függvény határának meghatározása egy pontban.

Az f-ii y \u003d f (x) határértéke az x 0 pontban (vagy az x x 0 pontban) az a szám, ha az argumentum bármely utolsó (x n) értékére az x 0-hoz konvergál ( mind x n x 0), az f-ii értékek sorozata (f(x n)) az a határértékhez konvergál.

Infinitezimális függvény definíciója.

funkció f(x) végtelenül kicsinek nevezzük x→A esetén, ha .

A meghatározás végtelen nagyszerű funkció.

funkció f(x) végtelen nagynak nevezzük x→A pontban, ha .

Alapértelmezett: A függvényt hívják elenyésző at , ha .

A " " jelölésben ezt feltételezzük x0 végső értéket vehet fel: x0= Const, és végtelen: x0= ∞.

Az infinitezimális függvények tulajdonságai:

1) Egy véges számú, végtelenül kicsi függvény algebrai összege végtelenül kicsi függvény esetén.

2) Függvényekre véges számú végtelenül kicsi szorzata függvényre végtelenül kicsi.

3) Műalkotás korlátozott funkció egy infinitezimális függvényhez egy infinitezimális függvény.

4) A hányadosa egy végtelenül kicsi függvényt osztunk egy olyan függvénnyel, amelynek határértéke nem nulla, egy függvénynél végtelenül kicsi.

Példa: Funkció y = 2 + x végtelenül kicsi a , mert .

Alapértelmezett: A függvényt hívják végtelenül nagy at , ha .

A végtelenül nagy függvények tulajdonságai:

1) Függvényekre a végtelenül nagy összege végtelenül nagy egy függvényre.

2) Egy függvény végtelen nagy szorzata egy olyan függvénnyel, amelynek határértéke nem nulla, végtelenül nagy egy függvényre.

3) Egy végtelenül nagy függvény és egy korlátos függvény összege végtelenül nagy függvény.

4) Ha egy függvény végtelenül nagyot elosztunk egy véges határértékkel rendelkező függvénnyel, akkor egy függvényre végtelenül nagy.

Példa: Funkció y= végtelenül nagy -ra, mert .

Tétel.Összefüggés a végtelenül kicsi és a végtelenül nagy mennyiségek között. Ha egy függvény végtelenül kicsi -ben, akkor a függvény végtelenül nagy -ben. Ezzel szemben, ha egy függvény végtelenül nagy -ben, akkor a függvény végtelenül kicsi -ben.

Két infinitezimális arányát általában a szimbólummal, két végtelenül nagyot a szimbólummal jelölik. Mindkét reláció határozatlan abban az értelemben, hogy korlátja létezhet vagy nem, egy bizonyos számmal egyenlő vagy végtelen, attól függően, hogy a határozatlan kifejezésekben milyen konkrét függvények vannak.

A határozatlan alakon és határozatlanon kívül a következő kifejezések vannak:

Az azonos előjelű végtelenül nagyok különbsége;

Egy infinitezimális és egy végtelen nagy szorzata;

Egy exponenciális hatványfüggvény, amelynek alapja 1-re, a mutatója pedig -ra;

Exponenciális-hatványfüggvény, melynek alapja végtelenül kicsi, kitevője pedig végtelenül nagy;

Exponenciális függvény, amelynek bázisa és kitevője végtelenül kicsi;

Exponenciális függvény, amelynek bázisa végtelenül nagy, kitevője pedig végtelenül kicsi.

Azt mondják, hogy van ennek megfelelő bizonytalanság. A limit számítását ezekben az esetekben nevezzük a bizonytalanság feltárása. A bizonytalanság feltárására a határjel alatti kifejezést olyan formává alakítjuk, amely nem tartalmaz bizonytalanságot.

A határértékek kiszámításakor a határértékek tulajdonságait, valamint a végtelenül kicsi és a végtelenül nagy függvények tulajdonságait használjuk.

Tekintsen példákat különféle határértékek számításaira.

1) . 2) .

4) , mert egy infinitezimális at függvény szorzata egy korlátos függvénnyel végtelenül kicsi.

5) . 6) .

7) = =

. Ebben az esetben a típus határozatlansága volt, amit polinomok faktorálásával és közös tényezővel való redukálással oldottak meg.

= .

Ebben az esetben a típus határozatlansága volt, amit úgy oldottak meg, hogy a számlálót és a nevezőt megszoroztuk a kifejezéssel, a képlet felhasználásával, majd a törtet (+1) csökkentettük.

9)
. Ebben a példában a típus bizonytalanságát úgy mutattuk ki, hogy a tört számlálóját és nevezőjét tagonként felosztottuk a legmagasabb fokozattal.

Figyelemre méltó határok

Az első csodálatos határ : .

Bizonyíték. Tekintsünk egy egységkört (3. ábra).

3. ábra. egységkör

Hadd x a középponti szög radián mértéke MOA(), akkor OA = R= 1, MK= bűn x, NÁL NÉL=tg x. A háromszögek területeinek összehasonlítása OMA, OTAés ágazatok OMA, kapunk:

,

.

Ossza el az utolsó egyenlőtlenséget a bűnnel x, kapunk:

.

Mivel a -ra, akkor a határértékek 5) tulajdonsága szerint

A honnan és az at reciproka, amit igazolni kellett.

Megjegyzés: Ha a függvény infinitezimális -nél, azaz. , akkor az első figyelemre méltó határ a következőképpen alakul:

.

Tekintsünk példákat az első figyelemre méltó határértéket használó határszámításokra.

Ennek a határértéknek a kiszámításakor azt használtuk trigonometrikus képlet: .

.

Tekintsünk példákat a határérték számításokra a második figyelemre méltó határérték használatával.

2) .

3) . Típus kétértelműség van. Cseréljünk akkor ; nál nél .

Infinitezimálisok és nagyok számítása

Infinitezimális számítás- infinitezimális értékekkel végzett számítások, amelyekben a származtatott eredményt végtelenül kicsinyek végtelen összegének tekintjük. Az infinitezimális számítás az általános koncepció differenciál- és integrálszámításhoz, amelyek a modern felsőbb matematika alapját képezik. Az infinitezimális mennyiség fogalma szorosan összefügg a határ fogalmával.

Elenyésző

Utóbbi a n hívott elenyésző, ha . Például egy számsorozat végtelenül kicsi.

A függvényt hívják végtelenül kicsi egy pont szomszédságában x 0 ha .

A függvényt hívják végtelenül kicsi a végtelenben, ha vagy .

Szintén végtelenül kicsi az a függvény, amely a függvény és a határértéke közötti különbség, vagyis ha , akkor f(x) − a = α( x) , .

végtelenül nagy

Az összes alábbi képletben az egyenlőségtől jobbra lévő végtelenség egy bizonyos jelet jelent ("plusz" vagy "mínusz"). Ez például a függvény x bűn x, mindkét oldalon korlátlan, nem végtelenül nagy a számára.

Utóbbi a n hívott végtelenül nagy, ha .

A függvényt hívják végtelenül nagy egy pont szomszédságában x 0 ha .

A függvényt hívják végtelenül nagy a végtelenben, ha vagy .

Infinitezimals és infinitezimals tulajdonságai

Infinitezimálisok összehasonlítása

Hogyan hasonlítsuk össze a végtelenül kicsi mennyiségeket?
Az infinitezimális mennyiségek aránya alkotja az úgynevezett bizonytalanságot.

Definíciók

Tegyük fel, hogy végtelenül kicsi ugyanazon α( x) és β( x) (vagy ami a definíció szempontjából nem fontos, infinitezimális sorozatok).

Az ilyen határértékek kiszámításához célszerű a L'Hospital szabályát használni.

Összehasonlítási példák

Használata O-a kapott eredmények szimbólumai a következő formában írhatók fel x 5 = o(x 3). Ebben az esetben a bejegyzések 2x 2 + 6x = O(x) és x = O(2x 2 + 6x).

Egyenértékű mennyiségek

Meghatározás

Ha , akkor infinitezimális α és β mennyiségeket hívunk egyenértékű ().
Nyilvánvaló, hogy az ekvivalens mennyiségek a végtelenül kicsi mennyiségek egy speciális esetét jelentik, ugyanolyan kicsinységekkel.

-ra a következő ekvivalencia viszonyok érvényesek (az úgynevezett figyelemre méltó határok következtében):

Tétel

Két végtelenül kicsi mennyiség hányadosának (arányának) határa nem változik, ha az egyiket (vagy mindkettőt) egy ekvivalens értékre cseréljük.

Ennek a tételnek gyakorlati jelentősége van a határok megtalálásában (lásd a példát).

Használati példa

Csere sénn 2x egyenértékű érték 2 x, kapunk

Történelmi vázlat

A "végtelenül kicsi" fogalmát az ókorban az oszthatatlan atomok fogalmával kapcsolatban tárgyalták, de nem került be a klasszikus matematikába. A 16. században újjáéledt az "oszthatatlanok módszere" - a vizsgált figura végtelen kis részekre osztása.

Az infinitezimális kalkulus algebraizálása a XVII. Ezeket olyan számértékekként kezdték meghatározni, amelyek kisebbek bármely véges (nem nulla) értéknél, és mégsem egyenlők nullával. Az elemzés művészete az infinitezimálisokat (differenciálokat) tartalmazó reláció felállításából, majd annak integrálásából állt.

Old school matematikusok vetették alá a koncepciót elenyésző kemény kritika. Michel Rolle azt írta, hogy az új kalkulus: ragyogó hibák halmaza»; Voltaire mérgezően rámutatott, hogy ez a számítás az olyan dolgok kiszámításának és pontos mérésének művészete, amelyek létezését nem lehet bizonyítani. Még Huygens is elismerte, hogy nem értette a magasabb rendű különbségek jelentését.

A sors iróniájának tekinthető a nem standard elemzések század közepén való megjelenése, amely bebizonyította, hogy az eredeti nézőpont - a tulajdonképpeni infinitezimálisok - is konzisztens és az elemzés alapjául vehető.

Lásd még

Wikimédia Alapítvány. 2010 .

Nézze meg, mi az "Infinitesimal" más szótárakban:

VÉGTELEN KICSI- változó valamilyen folyamatban, ha ebben a folyamatban végtelenül közelít (hajlik) a nullához ... Nagy Politechnikai Enciklopédia

elenyésző- ■ Valami ismeretlen, de a homeopátiához kapcsolódó... Közös Igazságok Lexikona