A válasz a B pont pályája - astroid s t)

A cikloid görbék nemcsak cikloidot, epi- és hipocikloidot tartalmaznak, hanem trochoidot, kardioidot, astroidot is, amelyeket az alábbiakban ismertetünk.

Az X, y koordináták ebben az esetben kielégítik az astroid egyenletet (91. ábra)

Kivétel ad (astroid)

Amikor p \u003d r \u003d (m \u003d 3), a hipocikloidot astroidnak nevezik (64. ábra), és az egyenletek x \u003d R os i y \u003d R sin "i vagy x -y \u003d" R.

Ha p = r = - (m = 3), a hipocikloidot astroidnak nevezzük (64. ábra), és az egyenletek a következőt öltik:

ábrán 72 Az AB = I szegmens 0 = 180°-os szögben az AB = I linkre van rögzítve. Ezért a Bi pont által megrajzolt asztroidot m6 szöggel elforgatjuk a B pont által megrajzolt asztroidhoz képest,

Vizsgáljuk meg a görbe érintőinek megrajzolásának kérdését a vizsgált mechanizmus segítségével. A fent megfogalmazott szabálynak megfelelően az astroid érintője a hajtókar OA vonalán levág egy szegmenst, amely megegyezik a (160) kifejezés jobb oldalán lévő tört nevezőjével. ábrán látható mechanizmussal kapcsolatban. 72, a levágandó szegmens méretét a (172) képlet határozza meg.

A gyakorlatban az astroidok építéséhez gyártási körülmények között minden egyenes vonalat, amelyben a mozgó

ábrán A 72. ábrán bemutattuk azt a mechanizmust, amely a 10. láncszem S és Si végeit két, egymáshoz képest 45°-kal elforgatott astroid mentén mozgatja.

Az (57) és (58) egyenlettel leírt görbe egy astroid típusú görbe lesz. Ennek a görbének a szimmetriatengelyei az Ax tengelyekkel alakulnak ki

Mutassuk meg az asztroid megjelenését a Re5>0 félsíkon, ahogy az a -ban történik.

Feltételezve, hogy a = p = 1, megszerkesztünk egy kontúrt, amelyben az astroid deformálódott (24. ábra).

A csúszkák / és 2 rögzített p és q vezetőben csúsztatnak, amelyek tengelyei egymásra merőlegesek. Az 1-2 csúszkák a és 6 ágai a 3 keresztes csúszkában csúsznak, amelyek tengelyei szintén egymásra merőlegesek. A 4-es láncszem a 3-as csúszkával belép a C forgáspárba, és az 5-ös kereszt alakú csúszkába csúszik, amely a 6-os láncszem tengelye mentén csúszik, amely az L és B forgáspárban található / és 2-es csúszkákkal. Amikor az I-től 2-ig csúszkák vezetők mentén mozognak és a K pont egy astroid ívet ír le, melynek egyenlete = ahol 1 - AB. Ebben az esetben a közvetlen vonal körbehajlik

A hipocikloidnak n - -1 csúcsa van, amelyek mindegyike a feszültségkoncentráció szempontjából egyenértékű a repedés végével (a PZO ábrán egy n = 3 astroid látható). Az ilyen típusú hibák meghatározhatják a rideg szilárdságát

Határozzuk meg az asztroid érintőjének egyenletét!

ábrán A 72. ábra egy tízlengőkaros mechanizmust mutat be, amelyet astroidok játszására terveztek. Az astroid egy közönséges hipocikloid m = modulussal, és egy 6. rendű algebrai görbe. Az astroid neve

Így a rajzon látható astroidok egyikének érintője a C és 5 ponton, a másik érintője pedig a C és S pontokon halad át. De a B és B pontok a B és B hajtórúd végei lambdaszerű csoport a Hart egyenesben. Ezért a B vége mindig a DDj link mentén, a B vége pedig a DDj-re visszaállított merőleges mentén fog csúszni a C pontból. Ebből következik, hogy a B pont által megrajzolt astroid a DD kapcsolat összes pozíciójának burkológörbéje. Az előzőek kiterjeszthetők a B ponttal reprodukált asztroidokra is, vagy az A-ból az I sugárral körülírt kör bármely pontjára.

Mint ismeretes, az astroid gyökere, ha az utóbbi szimmetriaközéppontját választjuk pólusnak, egy négyszirmú rózsa. Így elég meghosszabbítani az ABi = AB szakaszokat az ábrán. 72 (vagy a 73. ábrán) az AB \u003d ABi \u003d L méretre, hogy ezzel elérje

AZ IZIO-RY KULTÚRA VYATKIN FONTOS MECHANIZMUSÁJA AZ ASTROID SZAPORODÁSÁRA

A szárny elméletéhez közvetlenül kapcsolódó munka véget vetve megjegyezzük G.N. Babaeva On Flettner's rotor (Study of Sarat. State University, Pedagogical Faculty. Vol. VH. Issue 11, 1929), amelyben a szerző a szárnyak vizsgálatának szokásos módszerét alkalmazza két Flettner-rotor esetére. A szerző egyébként megmutatta, hogy a pillanatok sora ebben az esetben egy astroid. Vonatkozó

Negyedrendű vonal (görbe). egy negyedik fokú algebrai egyenlet által meghatározott egyenest hívjuk meg a derékszögű derékszögű koordinátákhoz képest. Az ötödik, hatodik és egyéb rendek vonalai (görbéi) hasonlóan vannak meghatározva.

A negyedrendű vonalak (görbék) halmaza már nem több tucat, hanem több ezer vonalat tartalmaz egy adott típusból. Az ötödik és hatodik rendű sorhalmazok még változatosabbak. Itt figyelembe vesszük bizonyos negyedik és magasabb rendű sorokat, amelyek rendelkeznek érdekes tulajdonságokés gyakorlati alkalmazások.

Lemniscate Bernoulli

Forduljunk a sík M pontja által leírt görbére úgy, hogy e pont két meghatározott F 1 és F 2 pontja közötti távolságok p szorzata változatlan maradjon. Az ilyen görbét lemniszkátának nevezik (a lemniscate görögül "szalagot" jelent). Ha az F 1 F 2 szakasz hossza c, akkor az F 1 F 2 szegmens O középpontjától az F1 és F2 közötti távolságok egyenlőek c / 2-vel, és ezeknek a távolságoknak a szorzata egyenlő - c 2 / 4. Először is követeljük meg, hogy a változatlan szorzat p értéke pontosan 2/4 legyen; azután

vonalrend transzcendens spirál

Rizs. 8

Az O pont a lemniszkátán fog feküdni, és maga a lemniszkát úgy fog kinézni, mint egy „fekvő nyolcas” (8. ábra). Ha az F 1 F 2 szakaszt mindkét irányban folytatjuk a lemniszkátussal való metszéspontig, akkor két A 1 és A 2 pontot kapunk. Az A 1 A 2 \u003d x távolságot egy ismert c távolságon keresztül fejezzük ki:

A lemniszkát gócok az F1 (? c; 0) és F2 (c; 0). Vegyünk egy tetszőleges M (x; y) pontot. A fókuszpontok és az M pont közötti távolságok szorzata

És definíció szerint egyenlő c2-vel:

Az egyenlet mindkét oldalát négyzetre emeljük:

Bontsa ki a zárójeleket a bal oldalon:

Kinyitjuk a zárójeleket, és összecsukjuk az összeg új négyzetét:

Kivesszük a közös tényezőt és átvisszük:

Ebben az esetben a a lemniszkátot leíró kör sugara. Egyszerű transzformációk elvégzése után egy explicit egyenletet kaphatunk:

Négyzetre emeljük és kinyitjuk a zárójeleket:

eszünkbe juttatjuk

Ez másodfokú egyenlet y tekintetében". Megoldva azt kapjuk

Ha átvesszük a gyökeret, és elvetjük a negatív második taggal rendelkező opciót, a következőt kapjuk:

ahol a pozitív változat a lemniszkátus felső felét határozza meg, a negatív változat az alsót.

Ha a p konstans szorzat értéke nem egyenlő 2/4-gyel, akkor a lemniszkát megváltoztatja alakját. És ha p kisebb, mint c 2 /4, a lemniszkát két oválisból áll, amelyek mindegyike tartalmazza az F 1 és F 2 pontot (9. ábra).

Rizs. 9

Hogy. p és c 2 /4 eltérő feltételekkel különböző típusú lemniszkátokat kapunk (10. ábra).

Rizs. 10

Vegyünk most tetszőleges számú pontot a síkon. F 1 , F 2 ,…, F n Kapjunk egy görbét, amelynek alakja attól függ, hogy az F 1 , F 2 ,…, F n pontok hogyan helyezkednek el egymáshoz képest, és mekkora a konstans szorzat értéke. Ezt a görbét n gócos lemniszkátnak nevezzük.

Fentebb két góccal rendelkező lemniszkátusokat vettünk figyelembe. Ha különböző számú gócot veszünk, különböző módon rendezzük el, és a távolságok szorzatához ezt vagy azt az értéket rendeljük, akkor a legfurcsább körvonalak lemniszkátusai nyerhetők. Vezessük el a ceruza hegyét egy bizonyos A ponttól anélkül, hogy levennénk a papírról, hogy végül visszatérjen az A kiindulási ponthoz. Ekkor egy bizonyos görbét ír le; csak azt követeljük meg, hogy ez a görbe sehol ne metszi egymást

Rizs. 11

maga. Nyilvánvalóan ilyen módon görbék készíthetők, amelyek például egy emberi fej vagy egy madár körvonalait tartalmazzák (11. ábra). Kiderült, hogy ilyen tetszőleges görbével meg lehet választani az n számot és a fókuszok elrendezését úgy

F 1 , F 2 ,…, F n

és rendeljen hozzá egy ilyen értéket a távolságok állandó szorzatához

МF 1 МF 2 … МF n = p

hogy a megfelelő lemniszkát szem szerint nem fog eltérni ettől a görbétől. Vagyis a lemniszkátot leíró M pont lehetséges eltérései a megrajzolt görbétől - nem haladják meg a ceruzavonás szélességét (a ceruzát tetszés szerint lehet előre kihegyezni, hogy a vonás nagyon jó legyen keskeny). Ezt a figyelemre méltó tényt, amely a sok gócú lemniszkátusok formáinak rendkívüli sokféleségéről és gazdagságáról beszél, a felsőbb matematika segítségével meglehetősen szigorúan, de nagyon nehezen bizonyítható.

Pascal csiga

Az M és M" pontok helye a ceruza vonalain (amelynek O középpontja egy R sugarú körön van) a távolságra a vonalak körrel metszéspontjának P pontjának mindkét oldalán; így PM = PM" = a. egyenlet derékszögű koordinátákkal: (x2 + y2 - 2Rx)2 - a2(x2 + y2) = 0, in poláris koordináták: r = 2R cos j + a. Ha a = 2R, a hurok összehúzódik egy pontig, ebben az esetben a Pascal cochlea kardioiddá változik. A név B. Pascal (1588-1651) francia tudósról kapta, aki először tanulmányozta.

Cikloid görbék

Képzeljük el, hogy egy bizonyos görbe úgy gördül el, hogy nem csúszik végig egy másik íven; bármely pont, amely mindig az első görbéhez kapcsolódik, új görbét ír le. Tehát elképzelhet egy ellipszist, amely egy másik ellipszisre gördül, és megvizsgálhatja azt a vonalat, amely mentén a középpontja el fog mozogni, vagy meghatározhatja az egyenes vonalban gördülő parabola fókuszának pályáját, és így tovább.

Az így kialakított görbék között olyan görbék különböztethetők meg, amelyek egy olyan pont pályái, amelyek állandóan össze vannak kötve egy körrel, amely úgy gördül, hogy közben nem csúszik végig egy másik körön. Az így kapott sorokat ún cikloidális.

Cikloid görbék kialakításakor az ábrázolási pont bizonyos távolságra elválik a generáló (mozgó) kör középpontjától. Egy adott esetben a generáló kör kerületén van. Ebben a feltételben a kapott görbék epicikloidokra és hipocikloidokra oszthatók, attól függően, hogy a generáló kör a rögzített kör külső oldalán vagy belsejében helyezkedik el.

Az algebrai görbék közé tartoznak az olyan jól ismert görbék, mint a kardioid, astroid, tekintsük ezeket a görbéket.

Kardioid

1. Az egyenlet. A kardioid úgy definiálható, mint egy r sugarú kör kerületén fekvő pont pályája, amely egy azonos sugarú rögzített kör kerülete mentén gördül. Így ez egy epicikloid lesz, amelynek m modulusa 1.

Ez a körülmény lehetővé teszi, hogy azonnal felírjuk a kardioid parametrikus egyenleteit, az m modulust eggyel helyettesítve az epicikloid fenti parametrikus egyenleteiben. Lesz:

A kardioid poláris egyenletének meghatározásához célszerű az A pontot pólusnak venni (13. ábra), és a poláris tengelyt az abszcissza mentén irányítani. Mivel az AOO 1 M négyszög egyenlő szárú trapéz lesz, így az M pont poláris szöge egyenlő lesz a generáló kör elfordulási szögével, azaz. t paraméter. Figyelembe véve ezt a körülményt, cseréljük le y-t az (1) rendszer második egyenletében sin t-n keresztül. Az így kapott egyenlőséget sin t-vel redukálva megkapjuk a kardioid poláris egyenletét

Rizs. 13

Ezen egyenlet szerint

arra a következtetésre juthatunk, hogy a kardioid Pascal egyik csigája. Ezért egy kör konchoidjaként definiálható.

A (2) egyenletet derékszögű koordináta-rendszerre fordítva a következőket kapjuk:

Ebből az egyenletből következik, hogy a kardioid egy 4. rendű algebrai görbe.

2. Tulajdonságok. Először is, mivel a kardioid egy epicikloid, amelynek m=1, ezért az előző bekezdésben tárgyalt epicikloidok összes tulajdonsága átvihető rá.

Itt vannak a jellemzők és a specifikációk.

1. A kardioid tetszőleges pontjában lévő érintő átmegy a generáló kör körének pontján, a körök érintkezési pontjával átlósan ellentétes, a normál pedig az érintkezési pontjukon.

2. A kardioid érintője és az érintkezési pont sugárvektora által bezárt szög egyenlő a sugárvektor által alkotott szög felével. poláris tengely. Igazán

Ebből az összefüggésből egyenesen következik, hogy a kardioid érintőjének az abszcissza tengellyel bezárt szöge megegyezik (az AMN háromszög külső szögével 14. ábra). Egy képlet birtokában bebizonyíthatjuk, hogy a póluson átmenő húr végein húzott kardioid érintői egymásra merőlegesek.

Valóban, azóta

Rizs. 14

Azt is megjegyezzük, hogy ezen érintők metszéspontjainak helye egy kör.

és a második érintő A paramétert ezekből az egyenletekből kihagyva megkapjuk a megadott kör egyenletét.

3. A görbületi sugarat a kardioid tetszőleges pontjában a képlet határozza meg

Az is kimutatható, hogy egy adott pontban a görbületi sugár a poláris normál N 2/3-a.

Valóban, ahonnan a (4) alapján kapjuk.Ez az összefüggés felhasználható a kardioid görbületi középpontjának megszerkesztésére.

4. A kardioid evolúciója, az epicikloid fejlődésének általános tulajdonsága szerint, szintén az adotthoz hasonló, 1/3-os hasonlósági együtthatójú kardioid lesz, amelyet az adotthoz képest egy-egy forgatással elforgatunk. szög 180°.

5. Az A ponttól egy tetszőleges M pontig tartó kardioid ív hosszát a képlet határozza meg

Ha az ív hosszát az A ponttól átlósan ellentétes A 1 ponttól számoljuk, akkor az ív hosszának meghatározására szolgáló képlet a következőképpen írható fel:

6. A kardioid természetes egyenletét akkor kapjuk meg, ha a paramétert kizárjuk a (4) és (6) egyenlőségből. Úgy fog kinézni

7. A kardioid által határolt területet a képlet határozza meg

és amint látható, egyenlő a generáló kör hatkerekű területével.

A teljes kardioid hosszát a képlet határozza meg

és amint látható, egyenlő a generáló kör nyolc átmérőjével. A kardioid tengelye körüli forgásával kapott test térfogata egyenlő

A kardioid tengelye körüli forgásával kapott test felülete egyenlő

Láttuk, hogy a kardioid szervesen kapcsolódik a körhöz. Ez egy körből és egy epicikloidból álló konchoid. Más a kapcsolata a körrel - a kardioid a kör egy részkorszaka egy ehhez a körhöz tartozó ponthoz képest.

Rizs. 15

Valóban, legyen OM az N pontba húzott 2r sugarú kör érintőjére ejtett merőleges.

Mivel OM \u003d OB + BM, vagy \u003d\u003d 2r cos + 2r, akkor az M pontok lokusza egy kardioid lesz, amelynek egyenlete \u003d 2r (1 + cos)

Végezetül megjegyezzük, hogy a kardioid is a szinuszos spirálok családjába tartozik, és egyedi tulajdonságai ismétlődnek. általános tulajdonságok ezek a görbék. Ezekből a tulajdonságokból különösen az következik, hogy a kardioid inverziója a csúcshoz képest parabolát ad.

Astroid

1. Tulajdonságok. Az astroid a hipocikloidok speciális esete, nevezetesen egy hipocikloid, amelynek m modulusa 1/4. Ez tehát egy r sugarú kör körén fekvő pont pályája, amely egy másik, rögzített kör belsejében gördül, amelynek R sugara négyszer nagyobb.

Az asztroid paraméteres egyenletei úgy kaphatók meg, hogy hipocikloidokat teszünk az egyenletekbe, m=1/4. Íme az egyenletek:

Rizs. 16

ahol t, mint korábban, a generáló kör elfordulási szöge (16. ábra)

A t paramétert az (1) egyenletekből kihagyva a következőt kapjuk:

A (2) egyenletből következik, hogy az astroid egy hatodrendű algebrai görbe.

Az astroid paraméteres egyenletei (1) redukálhatók a formára

Ezekből az egyenletekből a t paramétert kihagyva megkapjuk az astroid egyenlet gyakran használt alakját

Feltételezve a korábban levezetett általános összefüggésekben cikloid görbékre a modulust

m = -1/4, megkapjuk az astroid megfelelő összefüggéseit:

1) a görbületi sugarat az astroid egy tetszőleges pontjában a képlet határozza meg

2) az astroid A pontból egy tetszőleges M(t) pontba tartó ív hosszát a képlet határozza meg

az egyik ág hossza egyenlő és a teljes görbe hossza 6R;

3) az astroid természetes egyenletének megszerzéséhez először megjegyezzük, hogy ha az ívhossz kezdőpontja nem az A pont, amelyre t = 0, hanem az a pont, amelyre t = 0, akkor az ív hossza ívet a képlet határozza meg

kizárva a t paramétert az (5) és (6) egyenletből, megkapjuk az astroid természetes egyenletét

4) az astroid evolúciója is az adotthoz hasonló, 2-es hasonlósági együtthatójú asztroid, az adotthoz képest /4 szöggel elforgatva (16. ábra)

5) a teljes astroid által határolt terület egyenlő az astroid forgásával kapott test térfogatával, egyenlő 32/105 R 3

az asztroid forgásával kialakuló test felülete egyenlő

Térjünk most át az astroid néhány sajátos tulajdonságának figyelembevételére.

Az astroid egy állandó hosszúságú, végű szegmens burkológörbéje. amelyek két egymásra merőleges egyenes mentén csúsznak.

Ezeket az egyeneseket vesszük koordinátatengelynek, és az ND=R csúszó szakasz dőlésszögét jelölve (4. ábra) az ND egyenes egyenletét a következő formában kapjuk meg.

Megkülönböztetve ezt az egyenletet a paraméterhez képest, a következőt kapjuk:

Az utolsó egyenletből és a (7) egyenletből kihagyva a paramétert, a burkológörbe egyenlet olyan formában lesz, hogy pl. astroid.

A gyakorlatban az ND szakasz mozgatása az úgynevezett kardánkörök segítségével hajtható végre. Ezen R sugarú körök egyike mozdulatlan, a másik, kétszer kisebb r sugarú kör pedig a mozdulatlan kör belső oldalán gördül végig. A gördülőkör bármely két, egymással átlósan ellentétes pontja, N és D, az álló kör két egymásra merőleges átmérője, Ox és Oy mentén mozog. Nyilvánvaló, hogy a gördülő kör átmérőjének burkolata az asztroid lesz.

Rizs. 17	Rizs. 18

Az asztroida képződésének figyelembe vett módszere a következőképpen is értelmezhető. Egy ODCN téglalap, amelynek két oldala két egymásra merőleges egyenesen fekszik, úgy deformálódik, hogy az átlója R-vel egyenlő hosszúságú marad, az átló burkológörbéje asztroid lesz. Mivel ebben az esetben a C csúcsból a DN átlóba ejtett merőleges a burkológörbe normálisaként szolgál, az asztroid a téglalap C csúcsából az átlójába esett merőlegesek alapjainak helye.

Mert ezek az egyenletek a korábban vizsgált közvetlen astroidot fejezik ki.

- (a görög asztroncsillag és eidosz nézetből) lapos görbe, amelyet egy kör egy pontja ír le, amely belülről érint egy négyszeres sugarú rögzített kört, és csúszás nélkül gördül végig. A hipocikloidokhoz tartozik. Astroid algebrai ...... Nagy enciklopédikus szótár

Létezik., Szinonimák száma: 1 görbe (56) ASIS Szinonim szótár. V.N. Trishin. 2013... Szinonima szótár

- (a görög ástron csillag és éidos nézetből), lapos görbe, amelyet egy kör egy pontja ír le, amely egy négyszeres sugarú rögzített kör belsejét érinti, és csúszás nélkül gördül végig. A hipocikloidokhoz tartozik. Astroid...... enciklopédikus szótár

- (astro... gr. eidos view) mat. lapos görbe, amelyet egy kör pontja ír le, amely nem csúszik végig egy másik, rögzített kör belső oldalán, amelynek sugara négyszer nagyobb, mint az első köré; úgy néz ki, mint egy négyágú csillag. Új szótár … Orosz nyelv idegen szavak szótára

Lapos algebra. a rend ti ro görbéjét az élig az r sugarú kör pontja írja le, amely az R=4r sugarú kör belső oldalán gördül; hipocikloid r=4 modullal. Egyenlet derékszögű derékszögű koordinátákkal: Parametrikus. egyenletek... Matematikai Enciklopédia

A görbe vagy vonal egy geometriai fogalom, amelyet a különböző szakaszokon eltérően határoznak meg.

GÖRBE (vonal), mozgó pont vagy test által hagyott nyom. A görbét általában csak simán görbülő vonalként ábrázolják, például parabolát vagy kört. De a görbe matematikai fogalma magában foglalja mind az egyenest, mind a szakaszokból álló ábrákat, például egy háromszöget vagy négyzetet.

A görbék laposra és térbelire oszthatók. Egy síkgörbe, például egy parabola vagy egy egyenes két sík vagy egy sík és egy test metszéspontjában jön létre, és ezért teljes egészében egy síkban fekszik. Egy térbeli görbe, például egy spirálrugó alakú csavarvonal, nem kapható meg semmilyen felület vagy test síkkal való metszéspontjaként, és nem is fekszik egy síkban. A görbék zárt és nyitott formákra is feloszthatók. Egy zárt görbének, például egy négyzetnek vagy egy körnek nincs vége, pl. az ilyen görbét létrehozó mozgó pont periodikusan megismétli az útját.

A görbe olyan pontok lokusza vagy halmaza, amelyek eleget tesznek valamilyen matematikai feltételnek vagy egyenletnek.

Például egy kör a síkban lévő pontok helye, amelyek egyenlő távolságra vannak egy adott ponttól. Meghatározott görbék algebrai egyenletek, az úgynevezett algebrai görbék.

Például egy y = mx + b egyenes egyenlete, ahol m a meredekség és b az y tengelyen levágott szakasz, algebrai.

Olyan görbék, amelyek egyenletei transzcendentális függvényeket tartalmaznak, például logaritmusokat ill trigonometrikus függvények, transzcendentális görbéknek nevezzük.

Például y = log x és y = tg x transzcendentális görbék egyenletei.

Az algebrai görbe alakja meghatározható az egyenletének mértékével, amely egybeesik az egyenlet tagjainak legmagasabb fokával.

Ha az elsőfokú egyenlet, például Ax + By + C = 0, akkor a görbe egyenes alakja.

Ha egy másodfokú egyenlet pl.

Ax 2 + By + C = 0 vagy Ax 2 + By 2 + C = 0, akkor a görbe másodfokú, azaz. az egyik kúpszelvényt jelöli; az ilyen görbék közé tartoznak a parabolák, hiperbolák, ellipszisek és körök.

Felsoroljuk a kúpszeletek egyenleteinek általános formáit:

x 2 + y 2 \u003d r 2 - kör,

x 2 / a 2 + y 2 / b 2 \u003d 1 - ellipszis,

y \u003d ax 2 - parabola,

x 2 / a 2 - y 2 / b 2 \u003d 1 - hiperbola.

A harmadik, negyedik, ötödik, hatodik stb. egyenleteinek megfelelő görbék. fokokat a harmadik, negyedik, ötödik, hatodik stb. görbéinek nevezzük. rendelés. Általában minél magasabb az egyenlet foka, a több görbe nyitott görbéje lesz.

Sok összetett görbe különleges nevet kapott.

A cikloid egy síkgörbe, amelyet egy egyenes mentén gördülő kör fix pontja ír le, amelyet a cikloid generatrixának nevezünk; egy cikloid ismétlődő ívek sorozatából áll.

Az epicikloid egy olyan síkgörbe, amelyet egy kör fix pontja ír le, amely egy másik rögzített kör mentén gördül a körön kívül.

A hipocikloid egy síkgörbe, amelyet egy kör fix pontja ír le, amely belülről egy rögzített kör mentén gördül.

A spirál egy lapos görbe, amely egy fix pontból egy-egy kanyart leteker (vagy körbeteker).

A matematikusok ősidők óta tanulmányozzák a görbék tulajdonságait, és sok szokatlan görbe neve összefügg azoknak a nevével, akik először tanulmányozták őket. Ilyen például Arkhimédész spirálja, Agnesi fürtje, Dioklész ciszoidja, Nikomédész kochoidja és Bernoulli lemniszkátusa.

Az elemi geometria keretein belül a görbe fogalma nem kap külön megfogalmazást, és néha "hosszúság szélesség nélkül" vagy "egy ábra határaként" határozzák meg. Lényegében az elemi geometriában a görbék tanulmányozása a példák figyelembevételére korlátozódik (, , , satöbbi.). Általános módszerek híján az elemi geometria meglehetősen mélyen behatolt a konkrét görbék tulajdonságainak vizsgálatába (, néhányés még), minden esetben speciális technikákat alkalmazva.

A görbét leggyakrabban úgy határozzák meg, mint egy szegmenstől a következőig történő folyamatos leképezést:

Ebben az esetben a görbék eltérőek lehetnek, még akkor is, ha azokmérkőzés. Az ilyen görbéket únparaméterezett görbékvagy ha[ a , b ] = , módokon.

Néha a görbét legfeljebb -ig határozzák meg, azaz a minimális ekvivalencia relációig úgy, hogy a parametrikus görbék

egyenértékűek, ha létezik folyamatos (néha nem csökkenő) h szegmensből [ a 1 ,b 1 ] szegmensbe [ a 2 ,b 2 ], olyan, hogy

Az e reláció által meghatározottakat egyszerűen görbéknek nevezzük.

Analitikai definíciók

Az analitikus geometria kurzusain bebizonyosodott, hogy a derékszögű derékszögű (vagy akár általános affin) koordinátákkal írt sorok között általános egyenlet másodfokú

Ax 2 + 2Bxy + Cy 2 + 2Dx + 2Ey + F = 0

(ahol az A, B, C együtthatók legalább egyike nem nulla) csak a következő nyolc típusú vonal létezik:

a) ellipszis;

b) hiperbola;

c) parabola (nem degenerált másodrendű görbék);

d) metsző egyenes pár;

e) egy pár párhuzamos egyenes;

f) egy pár egybeeső vonal (egy vonal);

g) egy pont (másodrendű degenerált egyenesek);

h) pontokat nem tartalmazó "egyenes".

Ezzel szemben e nyolc típus bármelyik sorát derékszögű derékszögű koordinátákkal írjuk le valamilyen másodrendű egyenlettel. (Az analitikus geometria kurzusokon általában kilenc (nem nyolc) típusú kúpmetszetről beszélünk, mivel ezek megkülönböztetnek egy "képzeletbeli ellipszist" és egy "képzeletbeli párhuzamos egyenespárt" - geometriailag ezek a "vonalak" ugyanazok, mivel mindkettő nem tartalmaznak egyetlen pontot, hanem analitikusan különböző egyenletekkel írják fel őket.) Ezért a (degenerált és nem degenerált) kúpszeletek másodrendű egyenesekként is definiálhatók.

NÁL NÉLegy síkban lévő görbét olyan pontok halmazaként határozzuk meg, amelyek koordinátái kielégítik az egyenletetF ( x , y ) = 0 . Ugyanakkor a funkcióhozF korlátozásokat vezetnek be, amelyek garantálják, hogy ennek az egyenletnek végtelen számú nem egybeeső megoldása van, és

ez a megoldáskészlet nem tölti ki a "sík darabját".

Algebrai görbék

A görbék fontos osztálya azok, amelyekre a függvényF ( x , y ) vankét változóból. Ebben az esetben az egyenlet által meghatározott görbeF ( x , y ) = 0 , nak, nek hívják.

Az 1. fokú egyenlet által adott algebrai görbék: .

Egy 2. fokú egyenlet, amelynek végtelen számú megoldása van, meghatároz, azaz degenerált és nem degenerált.

Példák a 3. fokú egyenletek által adott görbékre: , .

Példák a 4. fokú görbékre: és .

Példa a 6. fokú görbére: .

Példa egy páros teljesítményegyenlettel definiált görbére: (multifokális).

Egyenletekkel meghatározott algebrai görbék magasabb fokozatok, figyelembe veszik. Ugyanakkor elméletük nagyobb összhangra tesz szert, ha a mérlegelést a -n hajtjuk végre. Ebben az esetben az algebrai görbét egy alakegyenlet határozza meg

F ( z 1 , z 2 , z 3 ) = 0 ,

ahol F három változóból álló polinom, amelyek pontok.

Görbe típusok

A síkgörbe olyan görbe, amelynek minden pontja ugyanabban a síkban van.

(egyszerű egyenes vagy jordán ív, kontúr is) egy síkban vagy térben lévő pontok halmaza, amelyek egy az egyhez és kölcsönösen folytonos összhangban vannak a szakaszokkal.

Útvonal - szegmens in .

olyan analitikus görbék, amelyek nem algebraiak. Pontosabban egy analitikus függvény (vagy többdimenziós esetben egy függvényrendszer) szintvonalán keresztül definiálható görbék.

szinuszos,

Ciklois,

Arkhimédész spirálja

traktor,

láncvonal,

Hiperbolikus spirál stb.

1. A görbék meghatározásának módjai:

analitikus - a görbét egy matematikai egyenlet adja meg;

grafika - a görbe vizuálisan van beállítva a grafikus információ hordozóján;

táblázatos - a görbét egy pontsorozat koordinátái adják meg.

parametrikus (a görbe egyenletének legáltalánosabb módja):

ahol - sima paraméterfunkciókt, és

(x") 2 + (y") 2 + (z") 2 > 0 (szabályszerűségi feltétel).

Gyakran kényelmes a görbeegyenlet invariáns és kompakt jelölése a következőkkel:

ahol a bal oldalon vannak a görbe pontjai, a jobb oldal pedig meghatározza annak függését valamilyen paramétertől t. Ezt a jelölést koordinátákkal bővítve megkapjuk az (1) képletet.

1. Ciklois.

A cikloid tanulmányozásának története olyan nagy tudósok, filozófusok, matematikusok és fizikusok nevéhez fűződik, mint Arisztotelész, Ptolemaiosz, Galilei, Huygens, Torricelli és mások.

Ciklois(tól tőlκυκλοειδής - kerek) - amely egy egyenesben csúszás nélkül gördülő kör határán fekvő pont pályájaként határozható meg. Ezt a kört generáló körnek nevezzük.

A görbeképzés egyik legrégebbi módja a kinematikai módszer, amelynél a görbét egy pont pályájaként kapjuk meg. A görbét, amelyet egy körre rögzített pont pályájaként kapunk, amely csúszás nélkül gördül egy egyenes mentén, egy kör vagy más görbe mentén, cikloidálisnak nevezzük, amelyet az alábbiakból fordítunk: görög kör alakút jelent, körre emlékeztet.

Tekintsük először azt az esetet, amikor a kör egy egyenes mentén gördül. Az egyenesben csúszás nélkül gördülő körön rögzített pont által leírt görbét cikloidnak nevezzük.

Egy R sugarú kör gördüljön egy a egyenes mentén. C egy körön rögzített pont, amely az idő kezdeti pillanatában A helyzetben van (1. ábra). Tegyünk egy egyenesre egy AB szakaszt, amely egyenlő a kör kerületével, azaz. AB \u003d 2 π R. Ezt a szakaszt 8 egyenlő részre osztjuk az A1, A2, ..., A8 \u003d B pontokkal.

Nyilvánvaló, hogy amikor a kör az a egyenes mentén gördülve tesz egy fordulatot, azaz. 360-kal elfordul, ekkor a (8) pozícióba kerül, és a C pont A pozícióból B pozícióba kerül.

Ha a kör fél teljes fordulatot tesz, i.e. 180-kal elfordul, ekkor a (4) pozícióba kerül, és a C pont a legmagasabb C4 pozícióba kerül.

Ha a kört 45-ös szögben elforgatjuk, akkor a kör az (1) pozícióba, a C pont pedig a C1 pozícióba kerül.

Az 1. ábrán a cikloid többi pontja is látható, amelyek megfelelnek a kör fennmaradó forgási szögeinek, amelyek 45 többszörösei.

A megszerkesztett pontokat sima görbével összekötve a cikloidnak egy olyan szakaszát kapjuk, amely megfelel a kör egy teljes fordulatának. A következő fordulatokkal ugyanazokat a szakaszokat kapjuk, pl. a cikloid egy periodikusan ismétlődő szakaszból fog állni, amelyet cikloidívnek neveznek.

Figyeljünk a cikloid érintőjének helyzetére (2. ábra). Ha a kerékpáros vizes úton közlekedik, akkor a kerékről leszakadt cseppek érintőlegesen a cikloidhoz repülnek, és pajzsok hiányában felfröcskölhetik a kerékpáros hátát.

Az első személy, aki a cikloidot tanulmányozta, Galileo Galilei (1564-1642) volt. A nevét is ő találta ki.

A cikloid tulajdonságai:

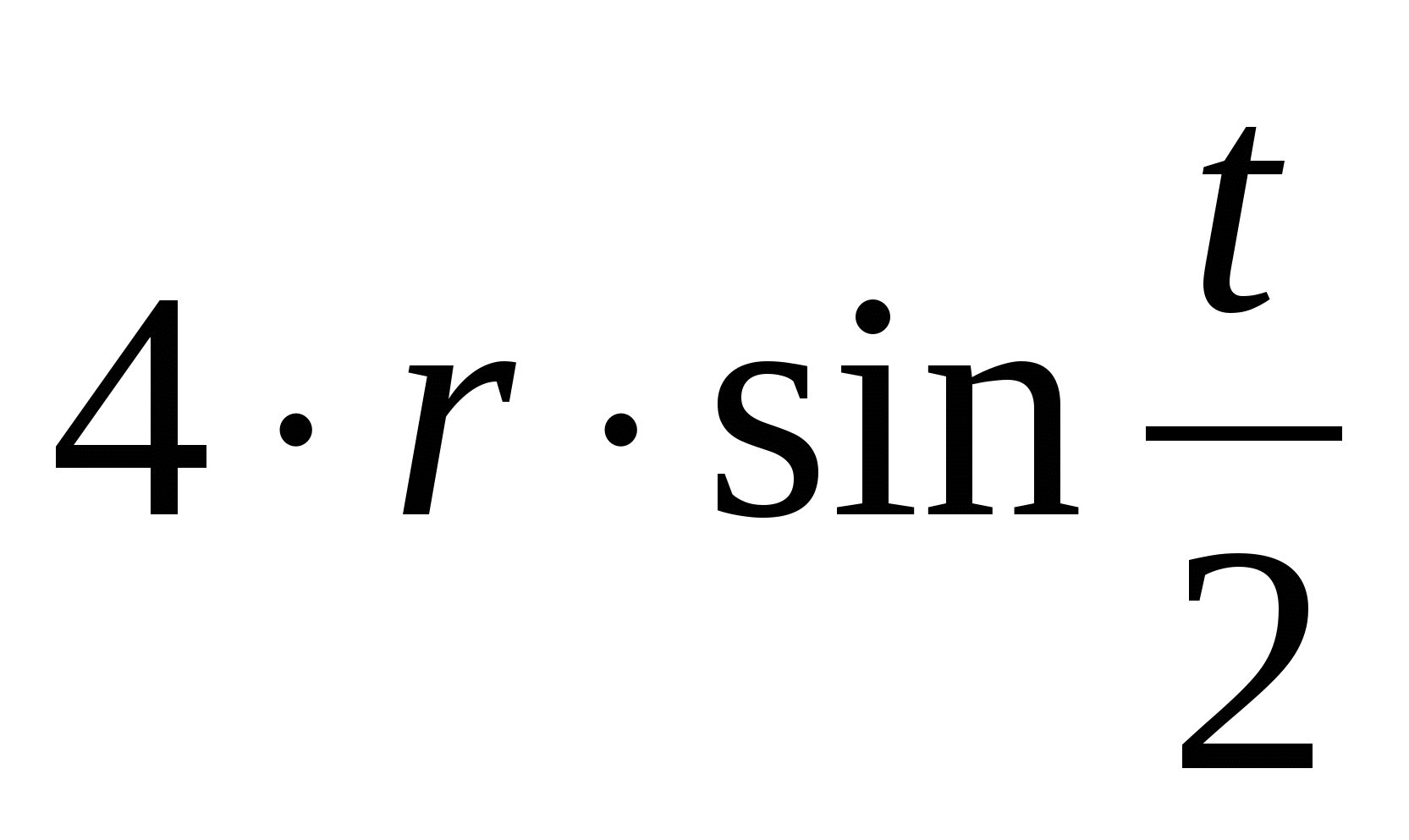
A cikloidnak számos figyelemre méltó tulajdonsága van. Említsünk meg néhányat közülük.

1. tulajdonság. (Jéghegy.) I. Bernoulli 1696-ban azt a feladatot tűzte ki célul, hogy megtalálja a legmeredekebb ereszkedési ívet, vagy más szóval azt a problémát, hogy milyen alakú legyen egy jégdomb ahhoz, hogy ösvényt lehessen készíteni kiindulópontÉs a legrövidebb idő alatt a B végpontig (3. ábra, a). A kívánt görbét "brachistochrone"-nak nevezték el, azaz. legrövidebb időgörbe.

Nyilvánvaló, hogy A pontból B pontba a legrövidebb út az AB szakasz. Ilyenekkel azonban egyenes vonalú mozgás a sebesség lassan nő, és az ereszkedésre fordított idő nagynak bizonyul (3. ábra, b).

A sebesség annál gyorsabb, annál meredekebb az ereszkedés. Meredek ereszkedés esetén azonban az ív mentén meghosszabbodik az út, és ezáltal megnő az áthaladási idő.

Azok a matematikusok, akik ezt a problémát megoldották: G. Leibniz, I. Newton, G. Lopital és J. Bernoulli. Bebizonyították, hogy a kívánt görbe egy fordított cikloid (3. ábra, a). A tudósok által a brachistochrone problémájának megoldására kidolgozott módszerek megalapozták a matematika új irányát - a variációszámítást.

2. tulajdonság. (Ingával ellátott óra.) A közönséges ingával ellátott óra nem tud pontosan futni, mivel az inga lengési periódusa az amplitúdójától függ: minél nagyobb az amplitúdó, annál hosszabb a periódus. A holland tudós, Christian Huygens (1629-1695) azon töprengett, hogy az ingahúron lévő golyónak melyik ívet kell követnie, hogy a rezgési periódus ne függjön az amplitúdótól. Figyeljük meg, hogy egy közönséges ingánál a görbe, amely mentén a labda mozog, egy kör (4. ábra).

A kívánt görbe egy fordított cikloidnak bizonyult. Ha például egy vályút fordított cikloid formájában készítenek, és egy golyót vezetnek át rajta, akkor a labda gravitációs mozgásának időtartama nem függ a kezdeti helyzetétől és amplitúdójától (5. ábra). . Ehhez a tulajdonsághoz a cikloidot "tautochrone"-nak is nevezik - egy egyenlő idők görbéje.

Huygens két cikloid alakú élű fatáblát készített, korlátozva a szál mozgását balra és jobbra (6. ábra). Ebben az esetben maga a golyó egy fordított cikloid mentén fog mozogni, és így rezgésének periódusa nem függ az amplitúdótól.

A cikloidnak ebből a tulajdonságából különösen az következik, hogy mindegy, hogy a fordított cikloid formájú jégcsúszdának melyik helyéről kezdjük az ereszkedést, ugyanannyi időt fogunk tölteni egészen a végpontig.

Cikloid egyenlet

1. A cikloid egyenletet célszerű felírni α - a kör forgási szöge radiánban kifejezve - szerint, vegye figyelembe, hogy α egyenlő a generáló kör által egyenesen megtett úttal is.

x=ra– r bűn α

y=r - r kötözősaláta α

2. Vegyük a vízszintes koordináta tengelyt egy egyenesnek, amely mentén a generáló sugarú kör gördül r.

A cikloid leírása parametrikus egyenletek

x = rt – r bűn t,

y = r – r kötözősaláta t.

Egyenlet itt:

A cikloidot oldat formájában kaphatjuk meg differenciálegyenlet:

A cikloid történetéből

A tudósok közül az első felhívta a figyelmet a cikloidraban ben, de ennek a görbének komoly tanulmányozása csak ben kezdődött.

Az első, aki elkezdte a cikloid tanulmányozását, Galileo Galilei (1564-1642), a híres olasz csillagász, fizikus és oktató volt. Ő alkotta meg a "cikloid" nevet is, ami azt jelenti: "körre emlékeztet". Galilei maga nem írt semmit a cikloidról, de ez irányú munkáit Galilei tanítványai és követői említik: Viviani, Toricelli és mások. Toricelli, a híres fizikus, a barométer feltalálója sok időt szentelt a matematikának. A reneszánsz korban nem voltak szűk szaktudósok. Egy tehetséges ember filozófiával, fizikával és matematikával foglalkozott, és mindenhol érdekes eredményeket ért el, és jelentős felfedezéseket tett. Kicsit később, mint az olaszok, a franciák felvették a cikloidot, és "roll"-nak vagy "trochoidnak" nevezték. 1634-ben Roberval - a súlyrendszer jól ismert súlyrendszerének feltalálója - kiszámította a cikloid íve és alapja által határolt területet. A cikloid érdemi tanulmányozását Galilei kortársa végezte el. Között, vagyis olyan görbék között, amelyek egyenlete nem írható fel alakjában x , y, a cikloid az első a vizsgáltak közül.

A cikloidról ezt írta:

A rulett olyan gyakori vonal, hogy az egyenes és a kör után nincs több közös vonal; olyan gyakran rajzolódik mindenki szeme elé, hogy meg kell lepődni, hogy a régiek nem vették észre... mert ez nem más, mint egy kerékszeggel leírt út a levegőben.

Az új görbe gyorsan népszerűvé vált, és mélyreható elemzésnek vetették alá, amely magában foglalta, , Newton,, a Bernoulli testvérek és a tudomány más fényesei a XVII-XVIII. században. A cikloidon a kialakuló módszerek azokban az években. Az a tény, hogy a cikloid analitikus vizsgálata ugyanolyan sikeresnek bizonyult, mint az algebrai görbék elemzése, nagy hatást keltett, és fontos érv lett az algebrai és transzcendentális görbék "jogegyenlítése" mellett. Epicikloid

A cikloidok bizonyos típusai

Epicikloid - a D átmérőjű körön fekvő A pont pályája, amely csúszás nélkül gördül végig egy R sugarú vezetőkör mentén (külső érintés).

Az epicikloid felépítése a következő sorrendben történik:

A 0 középpontból egy segédívet húzunk, amelynek sugara 000=R+r;

A 01, 02, ... 012 pontokból, mint a középpontokból, r sugarú köröket rajzolunk addig, amíg az epicikloidhoz tartozó A1, A2, ... A12 pontokban nem metszik egymást segédívekkel.

Hipocikloid

Hipocikloid - az A pont röppályája, amely egy D átmérőjű körön fekszik, és csúszás nélkül gördül egy R sugarú vezetőkör mentén (belső érintés).

A hipocikloid felépítése a következő sorrendben történik:

Az r sugarú generátorkört és az R sugarú vezetőkört úgy rajzoljuk meg, hogy az A pontban érintkezzenek;

A generáló kört 12 egyenlő részre osztjuk, megkapjuk az 1, 2, ... 12 pontokat;

A 0 középpontból egy 000=R-r sugarú segédívet húzunk;

Az a középső szöget az a \u003d 360r / R képlet határozza meg.

Az a szöggel behatárolt vezetőkör ívét 12 egyenlő részre osztjuk, 11, 21, ... 121 pontokat kapunk;

A 0 középponttól a 11, 21, ... 121 pontokig egyenesek húzódnak a 01, 02, ... 012 pontokban a segédívvel való metszéspontig;

A 0 középpontból a generáló kör 1, 2, ... 12 osztási pontjain keresztül segédíveket húzunk;

A 01, 02, ... 012 pontokból, mint a középpontokból, r sugarú köröket rajzolunk mindaddig, amíg a hipocikloidhoz tartozó A1, A2, ... A12 pontokban nem metszik egymást a segédívekkel.

1. Kardioid.

Kardioid ( καρδία - szív, A kardioid egy speciális eset A "kardioid" kifejezést Castillon vezette be 1741-ben.

Ha egy kört és egy pontot veszünk pólusnak, akkor csak akkor kapunk kardioidot, ha a kör átmérőjével megegyező szakaszokat félreteszünk. Az ábrázolt szegmensek egyéb értékei esetében a konchoidok megnyúltak vagy lerövidültek. Ezeket a megnyúlt és megrövidült kardioidokat egyébként Pascal-csigáknak nevezik.

Cardioidnak van különféle alkalmazások a technológiában. Kardioid formájában excentereket, bütyköket készítenek autókhoz. Néha fogaskerekek rajzolásakor használják. Ezenkívül az optikai technológiában is használják.

A kardioid tulajdonságai

Kardioid -M-ben egy mozgó kör egy zárt pályát ír le. Ezt a lapos görbét kardioidnak nevezik.

2) A kardioidot más módon is meg lehet szerezni. Jelölj egy pontot a körön Oés húzzon belőle egy gerendát. Ha egy pontból DE ennek a sugárnak a körrel való metszéspontját, halassza el a szakaszt délelőtt, a kör átmérőjével megegyező hossz mentén, és forgassuk el a gerendát a pont körül O, akkor a lényeg M a kardioid mentén fog mozogni.

3) Egy kardioidot úgy is ábrázolhatunk, mint egy görbe érintőt, amely az adott kör középpontjában lévő és a fix pontján áthaladó köröket érinti. Ha több kört építünk, a kardioidról kiderül, hogy úgy épül fel, mintha magától épülne fel.

4) Van egy másik olyan elegáns, mint váratlan módja a kardioid megtekintésének. Az ábrán egy körön egy pontszerű fényforrás látható. Miután a fénysugarak először verődnek vissza a körről, érintik a kardioidot. Képzelje el, hogy a kör a csésze szélei, és egy ponton egy erős izzót tükröz. Fekete kávét öntenek a csészébe, így láthatja a fényesen visszavert sugarakat. Ennek eredményeként a kardioidot kiemelik a fénysugarak.

1. Astroid.

Astroid (a görög astron - csillag és eidos - nézetből), lapos görbe, amelyet egy kör egy pontja ír le, amely érinti egy négyszeres sugarú rögzített kör belsejét, és csúszás nélkül gördül végig. A hipocikloidokhoz tartozik. Astroid - 6. rendű algebrai görbe.

Astroid.

A teljes astroid hossza a rögzített kör hat sugarával egyenlő, az általa határolt terület pedig a rögzített kör háromnyolcada.

Az asztroid érintőjének szegmense, amely a rögzített kör két egymásra merőleges sugara közé van zárva, és az asztroid csúcsára húzódik, egyenlő a rögzített kör sugarával, függetlenül attól, hogy a pontot hogyan választották ki.

astroid tulajdonságok

Van négyholdcsúcs .

Ívhossz a 0 ponttól a borítékig

állandó hosszúságú szakaszok családjai, amelyek végei két egymásra merőleges egyenesen helyezkednek el.

Az astroid a 6. rendű.

Astroid egyenletek

A derékszögű derékszögű koordinátákban megadott egyenlet:| x | 2/3 + | y | 2/3 = R2/3parametrikus egyenlet:x = Rcos 3 t y = Rsin 3 t

Hogyan építsünk astroidot

Rajzolunk két egymásra merőleges egyenest, és rajzolunk egy sorozat hosszúságú szakasztR amelyek végpontjai ezeken az egyeneseken fekszenek. Az ábrán 12 ilyen szakasz látható (beleértve magukat az egymásra merőleges egyenesek szakaszait is). Minél több szakaszt rajzolunk, annál pontosabb lesz a görbe. Most készítsük el ezen szegmensek burkológörbéjét. Ez a boríték lesz az astroid.

1. Következtetés

A dolgozat példákat ad különböző típusú görbékkel, különböző egyenletekkel definiált vagy valamilyen matematikai feltételt kielégítő problémákra. Különösen a cikloid görbék, azok meghatározásának módjai, különböző módokon konstrukciók, ezen görbék tulajdonságai.

A cikloid görbék tulajdonságait nagyon gyakran alkalmazzák a mechanikában a fogaskerekekben, ami jelentősen megnöveli a mechanizmusok alkatrészeinek szilárdságát.