Nézzünk egy sorozatot.

7 28 112 448 1792...

Teljesen egyértelmű, hogy bármelyik elemének értéke pontosan négyszer nagyobb, mint az előzőé. Tehát ez a sorozat egy előrelépés.

A geometriai progresszió egy végtelen számsorozat, amelynek fő jellemzője, hogy a következő számot valamilyen meghatározott számmal megszorozva kapjuk az előzőből. Ezt a következő képlet fejezi ki.

a z +1 =a z q, ahol z a kiválasztott elem száma.

Ennek megfelelően z ∈ N.

Az az időszak, amikor a geometriai haladást az iskolában tanulják, a 9. évfolyam. Példák segítenek megérteni a koncepciót:

0.25 0.125 0.0625...

A képlet alapján a progresszió nevezője a következőképpen kereshető:

Sem q, sem b z nem lehet nulla. Ezenkívül a progresszió egyik eleme sem lehet egyenlő nullával.

Ennek megfelelően, hogy megtudja a sorozat következő számát, meg kell szoroznia az utolsót q-val.

Ennek a folyamatnak a megadásához meg kell adnia annak első elemét és nevezőjét. Ezt követően meg lehet találni bármelyik következő kifejezést és azok összegét.

Fajták

q-tól és a 1-től függően ez a folyamat több típusra oszlik:

• Ha a 1 és q is nagyobb, mint egy, akkor egy ilyen sorozat minden következő elemmel növekvő geometriai sorozat. Az alábbiakban egy ilyen példát mutatunk be.

Példa: a 1 =3, q=2 - mindkét paraméter nagyobb egynél.

Azután numerikus sorozatígy írható:

3 6 12 24 48 ...

• Ha |q| egynél kisebb, azaz a vele való szorzás osztásnak felel meg, akkor a hasonló feltételek melletti progresszió csökkenő geometriai haladás. Az alábbiakban egy ilyen példát mutatunk be.

Példa: a 1 =6, q=1/3 - a 1 nagyobb, mint egy, q kisebb.

Ekkor a numerikus sorozat a következőképpen írható fel:

6 2 2/3 ... - bármely elem 3-szor nagyobb, mint az őt követő elem.

• Jel-változó. Ha q<0, то знаки у чисел последовательности постоянно чередуются вне зависимости от a 1 , а элементы ни возрастают, ни убывают.

Példa: a 1 = -3 , q = -2 - mindkét paraméter kisebb, mint nulla.

Ekkor a sorozat a következőképpen írható fel:

3, 6, -12, 24,...

Képletek

A geometriai progressziók kényelmes használatához számos képlet létezik:

• A z-edik tag képlete. Lehetővé teszi egy adott szám alatti elem kiszámítását az előző számok kiszámítása nélkül.

Példa:q = 3, a 1 = 4. Ki kell számítani a progresszió negyedik elemét.

Megoldás:a 4 = 4 · 3 4-1 = 4 · 3 3 = 4 · 27 = 108.

• Azon első elemek összege, amelyek száma z. Lehetővé teszi a sorozat összes elemének összegének kiszámításáta zinkluzív.

óta (1-q) a nevezőben van, akkor (1 - q)≠ 0, ezért q nem egyenlő 1-gyel.

Megjegyzés: ha q=1, akkor a progresszió egy végtelenül ismétlődő szám sorozata lenne.

Összeg geometriai progresszió, példák:a 1 = 2, q= -2. Számítsd ki az S 5-öt!

Megoldás:S 5 = 22 - számítás képlet alapján.

• Összeg, ha |q| < 1 и если z стремится к бесконечности.

Példa:a 1 = 2 , q= 0,5. Keresse meg az összeget.

Megoldás:Sz = 2 · = 4

Sz = 2 + 1 + 0.5 + 0.25 + 0.125 + 0.0625 = 3.9375 4

Néhány tulajdonság:

• jellemző tulajdonság. Ha a következő feltétel végeztek bármelyz, akkor az adott számsor egy geometriai progresszió:

a z 2 = a z -1 · az+1

• A geometriai haladás tetszőleges számának négyzetét úgy kapjuk meg, hogy összeadjuk egy adott sorozat bármely másik két számának négyzetét, ha azok egyenlő távolságra vannak ettől az elemtől.

a z 2 = a z - t 2 + a z + t 2 , aholta távolság ezek között a számok között.

• Elemekq-ban különbözikegyszer.
• A progressziós elemek logaritmusai is egy progressziót képeznek, de már aritmetikusak, vagyis mindegyik egy bizonyos számmal nagyobb, mint az előző.

Példák néhány klasszikus problémára

Ahhoz, hogy jobban megértsük, mi az a geometriai progresszió, segíthetnek a 9. osztályra vonatkozó megoldási példák.

• Feltételek:a 1 = 3, a 3 = 48. Keresse megq.

Megoldás: minden következő elem nagyobb, mint az előzőq egyszer.Egyes elemeket másokon keresztül kell kifejezni nevező használatával.

Következésképpen,a 3 = q 2 · a 1

Cserekorq= 4

• Feltételek:a 2 = 6, a 3 = 12. Számítsd ki az S 6 -ot!

Megoldás:Ehhez elég megkeresni q-t, az első elemet, és behelyettesíteni a képletbe.

a 3 = q· a 2 , Következésképpenq= 2

a 2 = q egy 1,ezért a 1 = 3

S 6 = 189

• · a 1 = 10, q= -2. Keresse meg a progresszió negyedik elemét.

Megoldás: ehhez elég a negyedik elemet az elsőn és a nevezőn keresztül kifejezni.

a 4 = q 3· a 1 = -80

Alkalmazási példa:

• A bank ügyfele 10 000 rubel összegű letétet helyezett el, amelynek feltételei szerint az ügyfél minden évben ennek 6% -át hozzáadja a tőkeösszeghez. Mennyi pénz lesz a számlán 4 év múlva?

Megoldás: A kezdeti összeg 10 ezer rubel. Tehát egy évvel a befektetés után a számlán 10 000 + 10 000 lesz az összeg · 0,06 = 10000 1,06

Ennek megfelelően a számlán lévő összeg egy év elteltével a következőképpen jelenik meg:

(10 000 1,06) 0,06 + 10 000 1,06 = 1,06 1,06 10 000

Vagyis minden évben 1,06-szorosára nő az összeg. Ez azt jelenti, hogy ahhoz, hogy 4 év elteltével meg lehessen találni a számlán lévő pénzeszközök összegét, elég megkeresni a progresszió negyedik elemét, amelyet az első 10 ezerrel egyenlő elem, a nevező pedig 1,06 ad meg.

S = 1,06 1,06 1,06 1,06 10000 = 12625

Példák az összeg kiszámításához szükséges feladatokra:

Különféle problémák esetén geometriai progressziót használnak. Az összeg megállapítására a következő példa adható:

a 1 = 4, q= 2, számítsd kiS5.

Megoldás: a számításhoz szükséges összes adat ismert, csak be kell cserélni a képletbe.

S 5 = 124

• a 2 = 6, a 3 = 18. Számítsd ki az első hat elem összegét!

Megoldás:

Geom. progresszió, minden következő elem q-szor nagyobb, mint az előző, vagyis az összeg kiszámításához ismerni kell az elemeta 1 és nevezőq.

a 2 · q = a 3

q = 3

Hasonlóképpen meg kell találnunka 1 , tudvána 2 Ésq.

a 1 · q = a 2

a 1 =2

S 6 = 728.

Tehát üljünk le és kezdjünk el néhány számot írni. Például:

Bármilyen számot írhat, és annyi lehet, amennyit akar (esetünkben ezek). Akárhány számot írunk, mindig meg tudjuk mondani, hogy melyik az első, melyik a második, és így tovább az utolsóig, vagyis meg tudjuk számozni. Ez egy példa egy számsorozatra:

Numerikus sorozat számok halmaza, amelyek mindegyikéhez egyedi szám rendelhető.

Például a sorozatunkhoz:

A hozzárendelt szám csak egy sorszámra vonatkozik. Más szóval, nincs három másodperces szám a sorozatban. A második szám (mint a -edik szám) mindig ugyanaz.

A számot tartalmazó számot a sorozat -edik tagjának nevezzük.

Általában az egész sorozatot valamilyen betűnek hívjuk (például), és ennek a sorozatnak minden tagja - ugyanaz a betű, amelynek indexe megegyezik ennek a tagnak a számával: .

A mi esetünkben:

A progresszió leggyakoribb típusai az aritmetikai és a geometriai. Ebben a témában a második fajtáról fogunk beszélni - geometriai progresszió.

Miért van szükségünk geometriai progresszióra és annak történetére?

Már az ókorban is az olasz matematikus, Leonardo pisai szerzetes (ismertebb nevén Fibonacci) foglalkozott a kereskedelem gyakorlati szükségleteivel. A szerzetes azzal a feladattal állt szemben, hogy megállapítsa, mi a legkisebb súlyszám, amellyel az árut le lehet mérni? Fibonacci írásaiban bebizonyítja, hogy egy ilyen súlyrendszer optimális: Ez az egyik első olyan helyzet, amikor az embereknek olyan geometriai progresszióval kellett megküzdeniük, amelyről valószínűleg hallottál, és legalábbis általános elképzelésed van róla. Miután teljesen megértette a témát, gondolja át, miért optimális egy ilyen rendszer?

Jelenleg az életgyakorlatban egy geometriai progresszió nyilvánul meg banki pénzbefektetésnél, amikor a számlán az előző időszakra felhalmozott összegre terhelik a kamat összegét. Vagyis ha egy takarékpénztárban lekötött betétre teszel le pénzt, akkor egy év múlva a betét az eredeti összeghez képest eggyel nő, pl. az új összeg a hozzájárulás szorzata lesz. Egy másik évben ez az összeg i.е. az ekkor kapott összeget ismét megszorozzuk és így tovább. Hasonló helyzetet írnak le a számítási problémáknál az ún kamatos kamat- a százalékot minden alkalommal a számlán lévő összegből veszik, figyelembe véve a korábbi kamatot. Ezekről a feladatokról egy kicsit később lesz szó.

Sok egyszerűbb eset van, amikor geometriai progressziót alkalmaznak. Például az influenza terjedése: az egyik ember megfertőzött egy embert, ő viszont megfertőzött egy másikat, és így a fertőzés második hulláma egy személy, és ő fertőzött meg egy másikat... és így tovább. .

Egyébként a pénzügyi piramis, ugyanaz az MMM, egy egyszerű és száraz számítás a geometriai progresszió tulajdonságai szerint. Érdekes? Találjuk ki.

Geometriai progresszió.

Tegyük fel, hogy van egy számsorunk:

Azonnal azt válaszolod, hogy könnyű, és egy ilyen sorozat neve a tagok különbségével van. Mit szólnál valami ehhez hasonlóhoz:

Ha kivonja az előző számot a következő számból, akkor látni fogja, hogy minden alkalommal, amikor új különbséget kap (és így tovább), de a sorozat határozottan létezik és könnyen észrevehető - minden következő szám szor nagyobb, mint az előző !

Ezt a sorozattípust ún geometriai progresszióés meg van jelölve.

A geometriai progresszió ( ) olyan numerikus sorozat, amelynek első tagja nullától eltérő, és a másodiktól kezdve minden tag megegyezik az előzővel, megszorozva ugyanazzal a számmal. Ezt a számot nevezzük a geometriai progresszió nevezőjének.

Azok a megkötések, amelyek szerint az első tag ( ) nem egyenlő, és nem véletlenszerűek. Tegyük fel, hogy nincs ilyen, és az első tag még mindig egyenlő, és q az, hmm .. legyen, akkor kiderül:

Egyetért azzal, hogy ez nem fejlődés.

Amint érti, ugyanazt az eredményt kapjuk, ha bármely szám nem nulla, de. Ezekben az esetekben egyszerűen nem lesz előrehaladás, mivel a teljes számsor vagy csupa nulla lesz, vagy egy szám, és az összes többi nulla.

Most beszéljünk részletesebben a geometriai progresszió nevezőjéről, azaz kb.

Ismét ez a szám hányszor változik minden következő tag geometriai progresszió.

Szerinted mi lehet? Ez így van, pozitív és negatív, de nem nulla (erről egy kicsit feljebb beszéltünk).

Tegyük fel, hogy van pozitívumunk. Legyen esetünkben a. Mi a második kifejezés és? Könnyen válaszolhatsz erre:

Rendben. Ennek megfelelően, ha, akkor a progresszió minden következő tagjának ugyanaz a jele - ők pozitív.

Mi van, ha negatív? Például a. Mi a második kifejezés és?

Ez egy teljesen más történet

Próbáld meg számolni ennek a haladásnak a tagját. mennyit kaptál? Nekem van. Így ha, akkor a geometriai progresszió tagjainak előjelei váltakoznak. Azaz, ha a tagjai között váltakozó előjelű progressziót látunk, akkor a nevezője negatív. Ez a tudás segíthet abban, hogy próbára tegye magát a témával kapcsolatos problémák megoldása során.

Most gyakoroljunk egy kicsit: próbáljuk meg meghatározni, hogy mely numerikus sorozatok geometriai, és melyek aritmetikai sorozatok:

Megvan? Hasonlítsa össze válaszainkat:

• Geometriai progresszió - 3, 6.
• Aritmetikai progresszió - 2, 4.
• Ez sem nem aritmetikai, sem nem geometriai sorozat - 1, 5, 7.

Térjünk vissza az utolsó folyamatunkhoz, és próbáljuk meg megtalálni a tagját ugyanúgy, mint az aritmetikában. Amint azt már sejtette, kétféleképpen lehet megtalálni.

Minden tagot egymás után szorozunk meg.

Tehát a leírt geometriai progresszió -edik tagja egyenlő.

Ahogy már sejti, most maga fog levezetni egy képletet, amely segít megtalálni a geometriai progresszió bármely tagját. Vagy már kihoztad magadnak, leírva, hogyan lehet lépésenként megtalálni a th tagot? Ha igen, akkor ellenőrizze érvelésének helyességét.

Illusztráljuk ezt a folyamat -edik tagjának megtalálásának példájával:

Más szavakkal:

Találja meg magának egy adott geometriai progresszió egy tagjának értékét.

Megtörtént? Hasonlítsa össze válaszainkat:

Ügyeljen arra, hogy pontosan ugyanazt a számot kapta, mint az előző módszernél, amikor egymás után szoroztuk a geometriai progresszió minden korábbi tagjával.
Próbáljuk meg „személyteleníteni” ezt a képletet – általános formába hozzuk, és megkapjuk:

A származtatott képlet minden értékre igaz - pozitív és negatív is. Ellenőrizd magad úgy, hogy kiszámítod a geometriai progresszió tagjait a következő feltételekkel: , a.

számoltál? Hasonlítsuk össze az eredményeket:

Egyetért azzal, hogy a progresszió tagját ugyanúgy meg lehetne találni, mint egy tagot, azonban fennáll a téves számítás lehetősége. És ha már megtaláltuk egy geometriai progresszió th tagját, a, akkor mi lehet egyszerűbb, mint a képlet „csonkított” részét használni.

Egy végtelenül csökkenő geometriai progresszió.

Nemrég beszéltünk arról, hogy mi lehet nagyobb vagy kisebb nullánál, de vannak speciális értékek, amelyekre a geometriai progressziót ún. végtelenül csökkenő.

Szerinted miért van ilyen neve?
Kezdésként írjunk fel néhány tagokból álló geometriai progressziót.
Akkor mondjuk:

Látjuk, hogy minden következő tag kisebb, mint az előző, de lesz-e szám? Azonnal nemmel válaszol. Éppen ezért a végtelenül csökkenő - csökken, csökken, de soha nem lesz nulla.

Annak érdekében, hogy világosan megértsük, hogyan néz ki ez vizuálisan, próbáljunk meg rajzolni egy grafikont a fejlődésünkről. Tehát esetünkben a képlet a következő formában jelenik meg:

A diagramokon megszoktuk, hogy függőséget építsünk a következőktől:

A kifejezés lényege nem változott: az első bejegyzésben egy geometriai progressziótag értékének a sorszámától való függését mutattuk be, a második bejegyzésben pedig egyszerűen egy geometriai progresziós tag értékét vettük fel, és a sorszámot nem nek, hanem asnak jelölték. Már csak a grafikon felrajzolása van hátra.
Lássuk, mit kaptál. Íme a diagram, amit kaptam:

Lát? A függvény csökken, nullára hajlik, de soha nem lépi át, tehát végtelenül csökken. Jelöljük a grafikonon pontjainkat, és egyúttal mit jelent a koordináta és a:

Próbáljon meg sematikusan ábrázolni egy geometriai progresszió grafikonját, ha az első tagja is egyenlő. Elemezze, mi a különbség az előző diagramunkhoz képest?

Sikerült? Íme a diagram, amit kaptam:

Most, hogy teljesen megértette a geometriai progresszió témakörének alapjait: tudja, mi az, tudja, hogyan találja meg a tagját, és azt is tudja, mi az a végtelenül csökkenő geometriai progresszió, térjünk át fő tulajdonságára.

geometriai progresszió tulajdonsága.

Emlékszel egy számtani sorozat tagjainak tulajdonságára? Igen, igen, hogyan lehet megkeresni egy bizonyos számú progresszió értékét, ha ennek a progressziónak a tagjainak vannak előző és későbbi értékei. Emlékezett? Ez:

Most pontosan ugyanazzal a kérdéssel állunk szemben a geometriai progresszió feltételeivel kapcsolatban. Egy ilyen képlet levezetéséhez kezdjük el a rajzolást és az érvelést. Meglátod, nagyon egyszerű, és ha elfelejted, magad is elő tudod hozni.

Vegyünk egy másik egyszerű geometriai folyamatot, amelyben ismerjük és. Hogyan lehet megtalálni? A számtani progresszióval ez könnyű és egyszerű, de hogy is van ez itt? Valójában a geometriában sincs semmi bonyolult - csak le kell festeni minden nekünk adott értéket a képlet szerint.

Kérdezi, és most mit csináljunk vele? Igen, nagyon egyszerű. Először is ábrázoljuk ezeket a képleteket az ábrán, és próbáljunk meg velük különféle manipulációkat végezni, hogy értéket kapjunk.

Elvonatkozunk a nekünk adott számoktól, csak a képlet segítségével történő kifejezésükre koncentrálunk. Meg kell találnunk a narancssárga színnel kiemelt értéket a mellette lévő kifejezések ismeretében. Próbáljunk meg velük különféle akciókat végrehajtani, aminek eredményeként kaphatunk.

Kiegészítés.
Próbáljunk meg két kifejezést hozzáadni, és a következőt kapjuk:

Ebből a kifejezésből, mint láthatja, semmilyen módon nem fogunk tudni kifejezni, ezért megpróbálunk egy másik lehetőséget - a kivonást.

Kivonás.

Amint látható, ebből sem tudunk kifejezni, ezért megpróbáljuk ezeket a kifejezéseket egymással szaporítani.

Szorzás.

Most alaposan nézzük meg, mi áll rendelkezésünkre, és szorozzuk meg a nekünk adott geometriai progresszió feltételeit ahhoz képest, amit találni kell:

Képzeld, miről beszélek? Helyesen, hogy megtaláljuk, a kívánt számmal szomszédos geometriai progressziószámok négyzetgyökét kell megszoroznunk egymással:

Tessék. Te magad vezetted le a geometriai progresszió tulajdonságát. Próbálja meg általános formában leírni ezt a képletet. Megtörtént?

Mikor felejtette el az állapotot? Gondolja át, miért fontos, például próbálja kiszámolni saját maga, a. Mi történik ebben az esetben? Így van, teljes hülyeség, hiszen a képlet így néz ki:

Ennek megfelelően ne felejtse el ezt a korlátozást.

Most számoljuk ki, mi az

Helyes válasz - ! Ha a számításnál nem felejtette el a második lehetséges értéket, akkor remek ember vagy, és azonnal folytathatja a képzést, ha pedig elfelejtette, olvassa el az alábbiakban elemzetteket, és figyeljen arra, hogy miért kell mindkét gyökeret beírni a válaszba .

Rajzoljuk meg mindkét geometriai progressziónkat – az egyiket értékkel, a másikat pedig egy értékkel, és ellenőrizzük, hogy mindkettőnek van-e létjogosultsága:

Annak ellenőrzéséhez, hogy létezik-e ilyen geometriai progresszió vagy sem, meg kell nézni, hogy minden adott tagja között azonos-e? Számítsa ki a q-t az első és a második esetre!

Látod, miért kell két választ írnunk? Mert a szükséges tag előjele attól függ, hogy pozitív vagy negatív! És mivel nem tudjuk, hogy mi az, mindkét választ plusz és mínusz jelekkel kell írnunk.

Most, hogy elsajátította a főbb pontokat és levezette a geometriai progresszió tulajdonságának képletét, keresse meg, ismerje meg és

Hasonlítsa össze válaszait a helyes válaszokkal:

Mit gondolsz, mi lenne, ha nem a kívánt számmal szomszédos, hanem attól egyenlő távolságra lévő geometriai progresszió tagjainak értékeit adnánk meg. Például meg kell találnunk, és adott és. Használhatjuk ebben az esetben az általunk levezetett képletet? Ugyanígy próbálja megerősíteni vagy cáfolni ezt a lehetőséget, és írja le, hogy az egyes értékek miből állnak, ahogyan a képlet kezdeti származtatásakor is tette.
Mit kaptál?

Most nézze meg újra figyelmesen.
és ennek megfelelően:

Ebből arra következtethetünk, hogy a képlet működik nem csak a szomszéddal egy geometriai progresszió kívánt tagjaival, hanem azzal is egyenlő távolságra abból, amit a tagok keresnek.

Így az eredeti képletünk a következő:

Vagyis ha az első esetben ezt mondtuk, akkor most azt mondjuk, hogy bármely kisebb természetes számmal egyenlő lehet. A lényeg, hogy mindkét megadott szám azonos legyen.

Gyakorolj konkrét példákon, csak légy nagyon óvatos!

1. , . Megtalálni.
2. , . Megtalálni.
3. , . Megtalálni.

Úgy döntött? Remélem, rendkívül figyelmes voltál, és észrevettél egy kis fogást.

Összehasonlítjuk az eredményeket.

Az első két esetben nyugodtan alkalmazzuk a fenti képletet, és a következő értékeket kapjuk:

A harmadik esetben a nekünk adott számok sorszámának alapos mérlegelése után megértjük, hogy azok nem egyforma távolságra vannak a keresett számtól: ez az előző szám, de helyben van eltávolítva, így nem lehetséges. a képlet alkalmazásához.

Hogyan lehet megoldani? Valójában nem olyan nehéz, mint amilyennek látszik! Írjuk fel veled, hogy az egyes nekünk adott számok és a kívánt számok miből állnak.

Tehát van és. Lássuk, mit tehetünk velük. Felosztást javaslom. Kapunk:

Adatainkat behelyettesítjük a képletbe:

A következő lépést megtalálhatjuk - ehhez meg kell vennünk a kapott szám kockagyökét.

Most pedig nézzük meg újra, mi van. Van, de meg kell találnunk, és ez viszont egyenlő:

A számításhoz minden szükséges adatot megtaláltunk. Helyettesítsd be a képletben:

A mi válaszunk: .

Próbáljon meg saját maga megoldani egy másik problémát:
Adott: ,
Megtalálni:

mennyit kaptál? Nekem van - .

Amint látja, valójában szüksége van rá csak egy képletre emlékezz- . A többit bármikor, nehézség nélkül visszavonhatja. Ehhez egyszerűen írja fel a legegyszerűbb geometriai folyamatot egy papírra, és írja le, hogy a fenti képlet szerint melyik számmal egyenlő.

Egy geometriai progresszió tagjainak összege.

Tekintsük most azokat a képleteket, amelyek lehetővé teszik, hogy gyorsan kiszámítsuk egy adott intervallumban a geometriai progresszió tagjainak összegét:

Egy véges geometriai haladás tagösszegének képletének levezetéséhez a fenti egyenlet minden részét megszorozzuk. Kapunk:

Nézd meg alaposan: mi a közös az utolsó két képletben? Így van, például a közös tagok és így tovább, kivéve az első és az utolsó tagot. Próbáljuk meg kivonni az 1. egyenletet a 2. egyenletből. Mit kaptál?

Most fejezze ki egy geometriai progresszió tagjának képletét, és helyettesítse be az eredményül kapott kifejezést az utolsó képletünkben:

Csoportosítsa a kifejezést. Meg kell szerezned:

Már csak annyit kell tenni, hogy kifejezzük:

Ennek megfelelően ebben az esetben.

Mi van ha? Milyen képlet működik akkor? Képzeljünk el egy geometriai progressziót itt. Írd őt körül? Helyesen azonos számok sorozata, a képlet így fog kinézni:

Az aritmetikai és geometriai progresszióhoz hasonlóan sok legenda létezik. Az egyik Seth legendája, a sakk megalkotója.

Sokan tudják, hogy a sakkjátékot Indiában találták fel. Amikor a hindu király találkozott vele, el volt ragadtatva a nő szellemességétől és a lehetséges pozíciók sokféleségétől. Amikor megtudta, hogy az egyik alattvalója találta ki, a király úgy döntött, hogy személyesen jutalmazza meg. Magához hívta a feltalálót, és megparancsolta, hogy bármit kérjen tőle, megígérte, hogy a legügyesebb vágyat is teljesíti.

Seta gondolkodási időt kért, és amikor másnap Seta megjelent a király előtt, meglepte a királyt kérésének páratlan szerénységével. Búzaszemet kért a sakktábla első mezőjére, búzát a másodikra, a harmadikra, a negyedikre stb.

A király mérges volt, és elűzte Sethet, mondván, hogy a szolga kérése méltatlan a királyi nagylelkűséghez, de megígérte, hogy a szolga megkapja a gabonáját a tábla összes cellájáért.

És most a kérdés a következő: a geometriai progresszió tagjainak összegének képletével számítsuk ki, hány szemcsét kell kapnia Sethnek?

Kezdjük a vitát. Mivel a feltétel szerint Seth búzaszemet kért a sakktábla első cellájába, a másodikba, a harmadikba, a negyedikbe stb., látjuk, hogy a probléma geometriai haladásról szól. Mi egyenlő ebben az esetben?
Jobb.

A sakktábla összes cellája. Illetve,. Minden adatunk megvan, már csak be kell pótolni a képletet és kiszámolni.

Ahhoz, hogy egy adott szám "skáláit" legalább megközelítőleg ábrázoljuk, transzformáljuk a fok tulajdonságait:

Persze ha akarod, elővehetsz egy számológépet, és kiszámolhatod, hogy milyen számra kerülsz, ha pedig nem, akkor szót kell fogadnod: a kifejezés végső értéke lesz.
Azaz:

kvintimillió kvadrillió billió milliárd millió ezer.

Fuh) Ha el akarja képzelni ennek a számnak a nagyságát, akkor becsülje meg, mekkora istállóra lenne szükség a teljes gabonamennyiség befogadásához.
M-es pajtamagasságnál és m-es szélességnél a hosszának km-re kellene kinyúlnia, i.e. kétszer olyan messze van a Földtől a Napig.

Ha a király erős lenne a matematikában, felkínálhatná magát a tudósnak, hogy számolja meg a szemeket, mert egy millió szem megszámlálásához legalább egy nap fáradhatatlan számolásra van szüksége, és tekintettel arra, hogy meg kell számolni a kvintilliókat, a szemeket egész életében számolni kellene.

És most megoldunk egy egyszerű feladatot egy geometriai progresszió tagjának összegén.
Vasya, az 5. osztályos tanuló megbetegedett influenzában, de továbbra is iskolába jár. Vasya minden nap két embert fertőz meg, akik viszont további két embert fertőznek meg, és így tovább. Csak egy ember az osztályban. Hány nap múlva lesz influenzás az egész osztály?

Tehát a geometriai progresszió első tagja Vasya, azaz egy személy. a geometriai progresszió tagja, ez az a két ember, akiket érkezése első napján fertőzött meg. Az előmeneteli tagok összege megegyezik az 5A tanulólétszámmal. Ennek megfelelően olyan fejlődésről beszélünk, amelyben:

Helyettesítsük be adatainkat a geometriai progresszió tagjainak összegének képletébe:

Az egész osztály megbetegszik napokon belül. Nem hiszel a képletekben és a számokban? Próbáld meg te magad ábrázolni a tanulók "fertőzését". Megtörtént? Nézze meg, hogy néz ki számomra:

Számítsd ki magad, hogy a tanulók hány napon kapnának influenzát, ha mindenki megfertőzne egy embert, és van egy személy az osztályban.

Milyen értéket kaptál? Kiderült, hogy egy nap után mindenki rosszul lett.

Mint látható, egy ilyen feladat és a hozzá tartozó rajz egy piramishoz hasonlít, amelyben minden következő új embereket „hoz”. Előbb-utóbb azonban eljön a pillanat, amikor ez utóbbi nem tud senkit vonzani. Esetünkben, ha azt képzeljük, hogy az osztály elszigetelődött, a származási személy zárja a láncot (). Így ha egy személy részt vesz egy pénzügyi piramisban, amelyben pénzt adtak, ha két másik résztvevőt hoz, akkor az illető (vagy általános esetben) nem hozna senkit, illetve mindent elveszítene, amit ebbe a pénzügyi átverésbe fektetett. .

Minden, amit fentebb elmondtunk, csökkenő vagy növekvő geometriai progresszióra vonatkozik, de, mint emlékszel, van egy különleges fajtánk - egy végtelenül csökkenő geometriai progresszió. Hogyan lehet kiszámítani a tagok összegét? És miért vannak ennek a fajta progressziónak bizonyos jellemzői? Találjuk ki együtt.

Tehát kezdésként nézzük meg újra ezt a képet egy végtelenül csökkenő geometriai progresszióról a példánkból:

És most nézzük meg a geometriai progresszió összegének képletét, amely egy kicsit korábban származott:
vagy

Mire törekszünk? Így van, a grafikonon látszik, hogy nullára hajlik. Azaz amikor majdnem egyenlő lesz, illetve a kifejezés kiszámításakor majdnem kapunk. Ebben a tekintetben úgy gondoljuk, hogy egy végtelenül csökkenő geometriai progresszió összegének kiszámításakor ez a zárójel elhanyagolható, mivel egyenlő lesz.

- a képlet egy végtelenül csökkenő geometriai sorozat tagjainak összege.

FONTOS! Csak akkor használjuk a képletet egy végtelenül csökkenő geometriai progresszió tagjainak összegére, ha a feltétel kifejezetten kimondja, hogy meg kell találnunk az összeget végtelen a tagok száma.

Ha egy adott n szám van feltüntetve, akkor az n tag összegének képletét használjuk, még akkor is, ha vagy.

És most gyakoroljunk.

1. Határozzuk meg egy geometriai haladás első tagjának összegét és segítségével.
2. Határozzuk meg egy végtelenül csökkenő geometriai progresszió tagjainak összegét a és -val.

Remélem nagyon óvatos voltál. Hasonlítsa össze válaszainkat:

Most már mindent tud a geometriai progresszióról, és ideje áttérni az elméletről a gyakorlatra. A vizsgán a leggyakoribb exponenciális problémák a kamatos kamatozású problémák. Róluk fogunk beszélni.

Problémák a kamatos kamat számításánál.

Biztosan hallott már az úgynevezett kamatos kamatformuláról. Érted, mire gondol? Ha nem, akkor találjuk ki, mert miután felismerte magát a folyamatot, azonnal megérti, mi köze ehhez a geometriai progressziónak.

Mindannyian bemegyünk a bankba, és tudjuk, hogy a betétekre különböző feltételek vonatkoznak: ez a futamidő, a további karbantartás és a kamat, kétféle számítási móddal - egyszerű és összetett.

TÓL TŐL egyszerű érdeklődés többé-kevésbé minden világos: a kamat egyszer kerül felszámításra a betéti futamidő végén. Vagyis ha évi 100 rubel alávetésről beszélünk, akkor csak az év végén írják jóvá. Ennek megfelelően a letét végére rubelt kapunk.

Kamatos kamat olyan lehetőség, amelyben kamatkapitalizáció, azaz a betét összegéhez való hozzászámításukat és a bevétel későbbi kiszámítását nem a kezdeti, hanem a felhalmozott betét összegéből. A nagybetűs írás nem állandóan, hanem bizonyos periodikusan történik. Általában az ilyen időszakok egyenlőek, és a bankok leggyakrabban egy hónapot, egy negyedévet vagy egy évet használnak.

Tegyük fel, hogy évente ugyanazt a rubelt helyezzük el, de a betét havi tőkésítésével. Mit kapunk?

Te mindent értesz itt? Ha nem, nézzük lépésről lépésre.

Rubelt vittünk a bankba. A hónap végére a számlánkon kell lennie egy összegnek, amely rubeleinkből és kamataiból áll, azaz:

Egyetért?

Kivehetjük a zárójelből, és a következőt kapjuk:

Egyetértek, ez a képlet már jobban hasonlít ahhoz, amit az elején írtunk. A százalékokkal kell foglalkozni

A probléma állapotában közöljük az évi. Mint tudod, mi nem szorozunk - a százalékokat tizedesjegyekké alakítjuk, azaz:

Jobb? Most azt kérdezed, honnan jött a szám? Nagyon egyszerű!
Ismétlem: a probléma állapota kb ÉVI felhalmozódott kamat HAVI. Tudniillik egy év hónapon belül a bank havi éves kamatot számít fel ránk:

Megvalósult? Most próbálja meg leírni, hogyan nézne ki a képletnek ez a része, ha azt mondanám, hogy a kamatot naponta számolják.
Sikerült? Hasonlítsuk össze az eredményeket:

Szép munka! Térjünk vissza a feladatunkhoz: írjuk meg, hogy a második hónapban mennyi kerül jóváírásra a számlánkon, figyelembe véve, hogy a felhalmozott betéti összeg után kamatot számítanak fel.
Íme, mi történt velem:

Vagy más szóval:

Úgy gondolom, hogy mindebben már észrevett egy mintát, és látott geometriai haladást. Írd meg, hogy mennyi lesz a tagja, vagyis mennyi pénzt kapunk a hónap végén.
Kész? Ellenőrzés!

Amint látja, ha egyszerű kamattal egy évre pénzt tesz egy bankba, akkor rubelt kap, ha pedig összetett kamatláb, akkor rubelt kap. A haszon csekély, de ez csak az év folyamán következik be, de hosszabb távon sokkal jövedelmezőbb a tőkésítés:

Fontolja meg a kamatos kamatozású probléma egy másik típusát. Azok után, amiket kitaláltál, elemi lesz számodra. Tehát a feladat:

A Zvezda 2000-ben kezdett befektetni az iparágba dollártőkével. 2001 óta minden évben az előző évi tőkével megegyező nyereséget termel. Mekkora nyereséget kap a Zvezda cég 2003 végén, ha a nyereséget nem vonják ki a forgalomból?

A Zvezda társaság tőkéje 2000-ben.
- a Zvezda társaság tőkéje 2001-ben.
- a Zvezda társaság tőkéje 2002-ben.
- a Zvezda társaság tőkéje 2003-ban.

Vagy írjuk röviden:

A mi esetünkben:

2000, 2001, 2002 és 2003.

Illetőleg:
rubel
Vegyük észre, hogy ebben a feladatban nincs osztás sem vele, sem szerint, mivel a százalékot ÉVESRE adjuk meg, és ÉVESRE számoljuk. Vagyis a kamatos kamat problémájának olvasásakor figyeljen arra, hogy hány százalékot adnak meg, és milyen időszakban kerül felszámításra, és csak ezután folytassa a számításokat.
Most már mindent tudsz a geometriai progresszióról.

Kiképzés.

1. Keresse meg a geometriai progresszió tagját, ha ismert, hogy és
2. Adja meg a geometriai haladás első tagjainak összegét, ha ismert, hogy és
3. Az MDM Capital 2003-ban kezdett befektetni az iparágba dollártőkével. 2004 óta minden évben az előző évi tőkével megegyező nyereséget termel. Az "MSK Cash Flows" cég 2005-ben kezdett befektetni az iparágba 10 000 dollár értékben, és 2006-ban kezdett el nyereséget termelni. Hány dollárral haladja meg egy cég tőkéje a másikét 2007 végén, ha a nyereséget nem vonják ki a forgalomból?

Válaszok:

1. Mivel a feladat feltétele nem mondja ki, hogy a progresszió végtelen, és meg kell találni egy bizonyos számú tagjának összegét, a számítást a következő képlet szerint végezzük:
2. 
   "MDM Capital" cég:

   2003, 2004, 2005, 2006, 2007.
   - 100%-kal, azaz 2-szeresére nő.
   Illetőleg:
   rubel
   MSK Cash flow:

   2005, 2006, 2007.
   - szorzattal növekszik.
   Illetőleg:
   rubel
   rubel

Foglaljuk össze.

1) A geometriai progresszió ( ) olyan numerikus sorozat, amelynek első tagja nullától eltérő, és a másodiktól kezdve minden tag megegyezik az előzővel, megszorozva ugyanazzal a számmal. Ezt a számot nevezzük a geometriai progresszió nevezőjének.

2) A geometriai progresszió tagjainak egyenlete -.

3) bármilyen értéket felvehet, kivéve a és.

• ha, akkor a progresszió minden további tagjának ugyanaz a jele – azok pozitív;
• ha, akkor a progresszió minden további tagja alternatív jelek;
• at - a progressziót végtelenül csökkenőnek nevezzük.

4) , at egy geometriai progresszió tulajdonsága (szomszédos tagok)

vagy
, at (egyenlő távolságra lévő kifejezések)

Ha megtaláltad, ne felejtsd el két válasznak kell lennie..

Például,

5) A geometriai sorozat tagjainak összegét a következő képlettel számítjuk ki:
vagy

vagy

FONTOS! Csak akkor használjuk a képletet egy végtelenül csökkenő geometriai haladás tagösszegére, ha a feltétel kifejezetten kimondja, hogy végtelen számú tag összegét kell megtalálni.

6) A kamatos kamatfeladatok számítása szintén a geometriai progresszió th tagjának képlete szerint történik, feltéve, hogy a pénzeszközöket nem vonták ki a forgalomból:

GEOMETRIAI PROGRESSZIÓ. RÖVIDEN A FŐRŐL

Geometriai progresszió( ) egy numerikus sorozat, amelynek első tagja nullától eltérő, és a másodiktól kezdve minden tag megegyezik az előzővel, megszorozva ugyanazzal a számmal. Ezt a számot hívják a geometriai progresszió nevezője.

Geometriai progresszió nevezője tetszőleges értéket vehet fel az és kivételével.

• Ha, akkor a progresszió minden további tagjának ugyanaz az előjele - pozitívak;
• ha, akkor a progresszió minden további tagja váltakozik az előjelekkel;
• at - a progressziót végtelenül csökkenőnek nevezzük.

Geometriai sorozat tagjainak egyenlete - .

Egy geometriai progresszió tagjainak összege képlettel számolva:
vagy

Ha a progresszió végtelenül csökken, akkor:

A FELÉPÍTETT 2/3 CIKKEK CSAK A YOUCLEVER DIÁKOK SZÁMÁRA ÉRHETŐK EL!

Legyél a YouClever tanulója,

Készüljön fel az OGE-re, vagy használja a matematikát "egy csésze kávé havonta" áron,

Továbbá korlátlan hozzáférést kap a "YouClever" tankönyvhöz, a "100gia" képzési programhoz (megoldáskönyv), korlátlan próba USE és OGE, 6000 feladat megoldások elemzésével és egyéb YouClever és 100gia szolgáltatásokkal.

A geometriai progresszió olyan numerikus sorozat, amelynek első tagja nem nulla, és minden következő tag egyenlő az előző taggal, megszorozva ugyanazzal a nullától eltérő számmal. A geometriai progressziót b1,b2,b3, …, bn, …

A geometriai progresszió tulajdonságai

A geometriai hiba bármely tagjának az előző tagjához viszonyított aránya azonos számmal, azaz b2/b1 = b3/b2 = b4/b3 = … = bn/b(n-1) = b(n+ 1)/bn = …. Ez közvetlenül következik az aritmetikai sorozat definíciójából. Ezt a számot nevezzük a geometriai progresszió nevezőjének. Általában a geometriai progresszió nevezőjét q betűvel jelöljük.

A geometriai progresszió beállításának egyik módja, ha beállítjuk annak első tagját b1 és a q geometriai hiba nevezőjét. Például b1=4, q=-2. Ez a két feltétel 4, -8, 16, -32, … geometriai progresszióját adja.

Ha q>0 (q nem egyenlő 1-gyel), akkor a progresszió az monoton sorozat. Például a 2, 4,8,16,32, ... sorozat egy monoton növekvő sorozat (b1=2, q=2).

Ha a geometriai hibában a nevező q=1, akkor a geometriai haladás minden tagja egyenlő lesz egymással. Ilyen esetekben a progressziót állandó sorozatnak mondják.

A progresszió n-edik tagjának képlete

Ahhoz, hogy a (bn) numerikus sorozat geometriai progresszió legyen, szükséges, hogy minden tagja a másodiktól kezdve a szomszédos tagok geometriai átlaga legyen. Vagyis teljesíteni kell a következő egyenletet - (b(n+1))^2 = bn * b(n+2), bármely n>0 esetén, ahol n a halmazhoz tartozik természetes számok N.

A geometriai sorozat n-edik tagjának képlete:

bn=b1*q^(n-1), ahol n az N természetes számok halmazába tartozik.

Vegyünk egy egyszerű példát:

Geometriai haladásban b1=6, q=3, n=8 keresse meg bn-t.

Használjuk a geometriai sorozat n-edik tagjának képletét.

Kapcsolódó lecke „Végtelenül csökkenő geometriai progresszió”

Az óra célja: a tanulók megismertetése egy újfajta sorozattal – egy végtelenül csökkenő geometriai progresszióval.

Feladatok:

a numerikus sorozat határának kezdeti ötletének megfogalmazása; megismerkedés a végtelen periodikus törtek közönségessé alakításának egy másik módszerével, a végtelenül csökkenő geometriai haladás összegének képletével;

iskolások személyiségének értelmi tulajdonságainak fejlesztése, mint pl logikus gondolkodás, az értékelő cselekvések, az általánosítás képessége;

tevékenységre nevelés, kölcsönös segítségnyújtás, kollektivizmus, a téma iránti érdeklődés.

Felszerelés: számítógép osztály, projektor, vetítővászon.

Az óra típusa: lecke - tanulás új téma.

Az órák alatt

én . Org. pillanat. Üzenet az óra témájával és céljával kapcsolatban.

II . A tanulók tudásának frissítése.1. Házi feladat ellenőrzése.

1) Az aritmetikai és geometriai folyamatokkal kapcsolatos alapképletek ellenőrzése. Két tanuló képleteket ír le a táblára.

2) A többi diák igen matematikai diktálás a "Summaképletek" témában.

Feladatok:

№1. Határozza meg egy aritmetikai sorozat első öt tagjának összegét, ha az első tagja 6 (1. lehetőség), -20 (2. lehetőség), az ötödik tagja pedig -6 (1. lehetőség), 20 (2. lehetőség).

№2. Határozzuk meg egy aritmetikai sorozat első öt tagjának összegét, ha az első tagja -20 (1. opció), 6 (2. opció), és a különbség 10 (1. opció), -3 (2. opció).

№3. Határozzuk meg egy geometriai progresszió első öt tagjának összegét, ha az első tagja 1 (1. lehetőség), -1 (2. opció), és a nevező -2 (1. lehetőség), 2 (2. opció).

A diktálás végén szelektíven két tanuló munkáját ellenőrzik értékelésre, a többiek önvizsgálatot végeznek a szerint. kulcsrakész megoldások a tábla hajtókáira írva.

Megoldások:

Feladatok

1. Az aritmetikai progressziót a képlet adja meg a n = 7 – 4 n. megtalálja a 10 . (-33)

2. Aritmetikai progresszió a 3 = 7 És a 5 = 1 . megtalálja a 4 . (4)

3. Aritmetikai progresszió a 3 = 7 És a 5 = 1 . megtalálja a 17 . (-35)

4. Aritmetikai progresszió a 3 = 7 És a 5 = 1 . megtalálja S 17 . (-187)

5. Geometriai progresszióhoz
találja meg az ötödik kifejezést.

6. Geometriai progresszióhoz
megtalálja n-th tag.

7. Exponenciálisan b 3 = 8 És b 5 = 2 . megtalálja b 4 . (4)

8. Exponenciálisan b 3 = 8 És b 5 = 2 . megtalálja b 1 És q .

9. Exponenciálisan b 3 = 8 És b 5 = 2 . megtalálja S 5 . (62)

III . Új téma felfedezése(bemutató bemutató).

Tekintsünk egy négyzetet, amelynek oldala egyenlő 1-gyel. Rajzoljunk egy másik négyzetet, amelynek az oldala az első négyzet fele, majd egy másik, amelynek az oldala a második fele, majd a következő és így tovább. Minden alkalommal az új négyzet oldala fele az előzőnek.

Ennek eredményeként a négyzetek oldalainak sorozatát kaptuk nevezővel geometriai progresszió kialakítása .

És ami nagyon fontos, minél több ilyen teret építünk, annál kisebb lesz a tér oldala. Például,

Azok. az n szám növekedésével a progresszió tagjai közelednek a nullához.

Ennek az ábrának a segítségével még egy sorozatot lehet figyelembe venni.

Például a négyzetek területeinek sorrendje:

. És még egyszer, ha n korlátlanul növekszik, ekkor a terület tetszőlegesen közelít a nullához.

Nézzünk még egy példát. Egyenlő oldalú háromszög, amelynek oldala 1 cm. Megszerkesztjük a következő háromszöget, amelynek csúcsai az 1. háromszög oldalainak felezőpontjaiban vannak, a következő tétel szerint. középső vonal háromszög - a 2. oldala egyenlő az első oldalának felével, a 3. oldala a 2. oldalának felével stb. Ismét megkapjuk a háromszögek oldalainak hosszsorozatát.

nál nél
.

Ha egy negatív nevezővel rendelkező geometriai progressziót tekintünk.

Aztán ismét növekvő számokkal n a progresszió feltételei közelítenek a nullához.

Figyeljünk ezeknek a sorozatoknak a nevezőire. A nevezők mindenhol kisebbek voltak, mint 1 modulo.

Megállapíthatjuk: egy geometriai progresszió végtelenül csökkenő lesz, ha nevezőjének modulusa kisebb, mint 1.

Elülső munka.

Meghatározás:

Egy geometriai progresszióról azt mondjuk, hogy végtelenül csökkenő, ha nevezőjének modulusa kisebb egynél.
.

A definíció segítségével meg lehet oldani azt a kérdést, hogy egy geometriai progresszió végtelenül csökkenő-e vagy sem.

Egy feladat

Végtelenül csökkenő geometriai progresszió-e a sorozat, ha a következő képlettel adjuk meg:

;
.

Megoldás:

. Találjuk ki q .

;
;
;
.

ez a geometriai progresszió végtelenül csökken.

b) ez a sorozat nem egy végtelenül csökkenő geometriai progresszió.

Tekintsünk egy négyzetet, amelynek oldala egyenlő 1-gyel. Oszd ketté, az egyik felét ismét félbe, és így tovább. a kapott téglalapok területei végtelenül csökkenő geometriai sorozatot alkotnak:

Az így kapott összes téglalap területének összege egyenlő lesz az 1. négyzet területével és 1-gyel.

De ennek az egyenlőségnek a bal oldalán végtelen számú tag összege található.

Tekintsük az első n tag összegét.

Egy geometriai sorozat első n tagjának összegére vonatkozó képlet szerint egyenlő .

Ha n akkor korlátlanul növekszik

vagy
. Ezért
, azaz
.

Egy végtelenül csökkenő geometriai progresszió összege sorozatkorlát van S 1 , S 2 , S 3 , …, S n , … .

Például egy progresszióhoz
,

Mivel

Egy végtelenül csökkenő geometriai progresszió összege képlet segítségével találhatjuk meg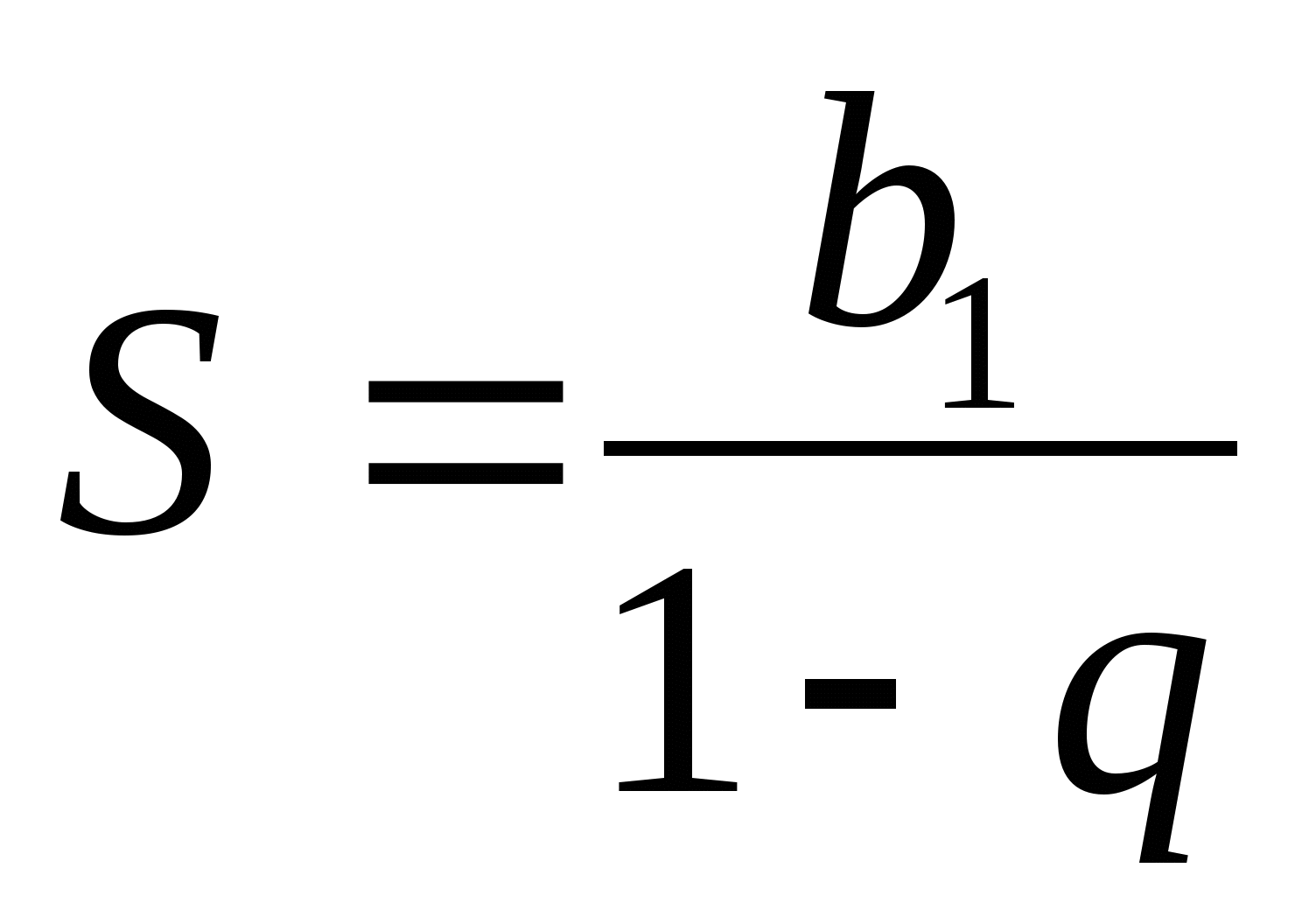
.

III . Reflexió és konszolidáció(feladatok elvégzése).

2. számú feladat. Határozzuk meg egy végtelenül csökkenő geometriai haladás összegét, amelynek az első tagja 3, a második 0,3.

Megoldás:

3. számú feladat. tankönyv, 160. o., 433. sz. (1)

Határozzuk meg egy végtelenül csökkenő geometriai progresszió összegét:

Megoldás:

4. számú feladat. Írj egy végtelen periodikust decimális 0,(5) közönséges törtként.

1. mód. Legyen x = 0, (5) = 0,555 ... / 10 2. módszer. 0,(5)=0,555…=

5. számú feladat. tankönyv, 162. o., 445. szám (3) ( független megoldás)

Írjuk fel a 0,(12) végtelen periodikus tizedes törtet közönséges törtnek!

Válasz: 0,(12)=4/33.

IV . Összegzés.

Milyen sorozattal találkoztál ma?

Határozzon meg egy végtelenül csökkenő geometriai progressziót.

Hogyan bizonyítható, hogy a geometriai progresszió végtelenül csökken?

Adja meg egy végtelenül csökkenő geometriai progresszió összegének képletét!

V . Házi feladat.

A geometriai progresszió olyan numerikus sorozat, amelynek első tagja nem nulla, és minden következő tag egyenlő az előző taggal, megszorozva ugyanazzal a nem nulla számmal.

A geometriai progressziót jelöljük b1,b2,b3, …, bn, … .

A geometriai hiba bármely tagjának az előző tagjához viszonyított aránya azonos számmal, azaz b2/b1 = b3/b2 = b4/b3 = … = bn/b(n-1) = b(n+ 1)/bn = …. Ez közvetlenül következik az aritmetikai sorozat definíciójából. Ezt a számot nevezzük a geometriai progresszió nevezőjének. Általában a geometriai progresszió nevezőjét q betűvel jelöljük.

Monoton és állandó sorrend

A geometriai progresszió beállításának egyik módja, ha beállítjuk annak első tagját b1 és a q geometriai hiba nevezőjét. Például b1=4, q=-2. Ez a két feltétel 4, -8, 16, -32, … geometriai progresszióját adja.

Ha q>0 (q nem egyenlő 1-gyel), akkor a progresszió az monoton sorozat. Például a 2, 4,8,16,32, ... sorozat egy monoton növekvő sorozat (b1=2, q=2).

Ha a geometriai hibában a nevező q=1, akkor a geometriai haladás minden tagja egyenlő lesz egymással. Ilyen esetekben a progresszióról azt mondják állandó sorrend.

Egy geometriai sorozat n-edik tagjának képlete

Ahhoz, hogy a (bn) numerikus sorozat geometriai progresszió legyen, szükséges, hogy minden tagja a másodiktól kezdve a szomszédos tagok geometriai átlaga legyen. Vagyis teljesíteni kell a következő egyenletet
(b(n+1))^2 = bn * b(n+2), bármely n>0 esetén, ahol n az N természetes számok halmazához tartozik.

A geometriai sorozat n-edik tagjának képlete:

bn=b1*q^(n-1),

ahol n az N természetes számok halmazához tartozik.

Egy geometriai folyamat első n tagjának összegének képlete

A geometriai folyamat első n tagjának összegének képlete:

Sn = (bn*q - b1)/(q-1), ahol q nem egyenlő 1-gyel.

Vegyünk egy egyszerű példát:

Geometriai haladásban b1=6, q=3, n=8 keresse meg Sn-t.

Az S8 meghatározásához a geometriai folyamat első n tagjának összegének képletét használjuk.

S8= (6*(3^8 -1))/(3-1) = 19680.