Osnovne elementarne funkcije, njihova inherentna svojstva i odgovarajući grafovi su jedna od osnova matematičkog znanja, slična po važnosti tablici množenja. Elementarne funkcije su osnova, podrška za proučavanje svih teorijskih pitanja.

Članak u nastavku pruža ključni materijal na temu osnovnih elementarnih funkcija. Uvest ćemo pojmove, dati im definicije; Hajde da detaljno proučimo svaku vrstu elementarnih funkcija i analiziramo njihova svojstva.

Razlikuju se sljedeće vrste osnovnih elementarnih funkcija:

Definicija 1

• konstantna funkcija (konstanta);
• korijen n-tog stepena;
• funkcija snage;
• eksponencijalna funkcija;
• logaritamska funkcija;
• trigonometrijske funkcije;
• bratske trigonometrijske funkcije.

Konstantna funkcija je definirana formulom: y = C (C je neki realan broj) i također ima ime: konstanta. Ova funkcija određuje da li bilo koja realna vrijednost nezavisne varijable x odgovara istoj vrijednosti varijable y – vrijednosti C.

Grafikon konstante je prava linija koja je paralelna sa x-osi i prolazi kroz tačku koja ima koordinate (0, C). Radi jasnoće, predstavljamo grafike konstantnih funkcija y = 5 , y = - 2 , y = 3 , y = 3 (na crtežu su označene crnom, crvenom i plavom bojom).

Definicija 2

Ova elementarna funkcija je definirana formulom y = x n (n - prirodni broj više od jedne).

Razmotrimo dvije varijacije funkcije.

1. Koren n-tog stepena, n je paran broj

Radi jasnoće, ukazujemo na crtež koji prikazuje grafikone takvih funkcija: y = x , y = x 4 i y = x 8 . Ove funkcije su označene bojama: crna, crvena i plava, respektivno.

Sličan pogled na grafove funkcije parnog stepena za druge vrijednosti indikatora.

Definicija 3

Svojstva korijena funkcije n-tog stepena, n je paran broj

• domen definicije je skup svih nenegativnih realni brojevi [ 0 , + ∞) ;
• kada je x = 0, funkcija y = x n ima vrijednost jednaku nuli;
• ova funkcija je funkcija opšti pogled(nije ni paran ni neparan);
• raspon: [ 0 , + ∞) ;
• ova funkcija y = x n s parnim eksponentima korijena raste u cijelom domenu definicije;
• funkcija ima konveksnost sa smjerom prema gore u cijeloj domeni definicije;
• nema pregibnih tačaka;
• nema asimptota;
• graf funkcije za parno n prolazi kroz tačke (0 ; 0) i (1 ; 1) .

1. Koren n-tog stepena, n je neparan broj

Takva funkcija je definirana na cijelom skupu realnih brojeva. Radi jasnoće, razmotrite grafove funkcija y = x 3 , y = x 5 i x 9 . Na crtežu su označene bojama: crna, crvena i plava boja krivulja, respektivno.

Druge neparne vrijednosti eksponenta korijena funkcije y = x n dat će graf sličnog oblika.

Definicija 4

Svojstva korijena funkcije n-tog stepena, n je neparan broj

• domen definicije je skup svih realnih brojeva;
• ova funkcija je neparna;
• raspon vrijednosti je skup svih realnih brojeva;
• funkcija y = x n sa neparnim eksponentima korijena raste u cijelom domenu definicije;
• funkcija ima konkavnost na intervalu (- ∞ ; 0 ] i konveksnost na intervalu [ 0 , + ∞) ;
• tačka pregiba ima koordinate (0 ; 0) ;
• nema asimptota;
• graf funkcije za neparan n prolazi kroz tačke (- 1 ; - 1) , (0 ; 0) i (1 ; 1) .

Funkcija napajanja

Definicija 5

Funkcija snage je definirana formulom y = x a .

Tip grafova i svojstva funkcije zavise od vrijednosti eksponenta.

• kada funkcija stepena ima celobrojni eksponent a, tada oblik grafa funkcije stepena i njena svojstva zavise od toga da li je eksponent paran ili neparan, kao i koji predznak ima eksponent. Razmotrimo sve ove posebne slučajeve detaljnije u nastavku;
• eksponent može biti razlomačan ili iracionalan - ovisno o tome, tip grafova i svojstva funkcije također variraju. Posebne slučajeve ćemo analizirati postavljanjem nekoliko uslova: 0< a < 1 ; a > 1 ; - 1 < a < 0 и a < - 1 ;
• funkcija stepena može imati nulti eksponent, u nastavku ćemo također detaljnije analizirati ovaj slučaj.

Analizirajmo funkciju snage y = x a kada je a neparno pozitivan broj, na primjer, a = 1 , 3 , 5 ...

Radi jasnoće, ukazujemo na grafove takvih funkcija stepena: y = x (crna boja grafikona), y = x 3 (plava boja grafikona), y = x 5 (crvena boja grafikona), y = x 7 (zeleni grafikon). Kada je a = 1, dobijamo linearnu funkciju y = x.

Definicija 6

Svojstva funkcije stepena kada je eksponent neparan pozitivan

• funkcija raste za x ∈ (- ∞ ; + ∞) ;
• funkcija je konveksna za x ∈ (- ∞ ; 0 ] i konkavna za x ∈ [ 0 ; + ∞) (isključujući linearnu funkciju);
• tačka pregiba ima koordinate (0 ; 0) (isključujući linearnu funkciju);
• nema asimptota;
• prolazne tačke funkcije: (- 1 ; - 1) , (0 ; 0) , (1 ; 1) .

Analizirajmo funkciju snage y = x a kada je a paran pozitivan broj, na primjer, a = 2 , 4 , 6 ...

Radi jasnoće, ukazujemo na grafikone takvih funkcija snage: y \u003d x 2 (crna boja grafikona), y = x 4 (plava boja grafikona), y = x 8 (crvena boja grafikona). Kada je a = 2, dobijamo kvadratnu funkciju čiji je graf kvadratna parabola.

Definicija 7

Svojstva funkcije stepena kada je eksponent čak pozitivan:

• domen definicije: x ∈ (- ∞ ; + ∞) ;
• opadajuće za x ∈ (- ∞ ; 0 ] ;
• funkcija je konkavna za x ∈ (- ∞ ; + ∞) ;
• nema pregibnih tačaka;
• nema asimptota;
• prolazne tačke funkcije: (- 1 ; 1) , (0 ; 0) , (1 ; 1) .

Na slici ispod prikazani su primjeri grafova eksponencijalne funkcije y = x a kada je a neparan negativan broj: y = x - 9 (crna boja grafikona); y = x - 5 (plava boja grafikona); y = x - 3 (crvena boja grafikona); y = x - 1 (zeleni grafikon). Kada je \u003d - 1, dobijamo inverznu proporcionalnost, čiji je graf hiperbola.

Definicija 8

Svojstva funkcije snage kada je eksponent neparno negativan:

Kada je x = 0, dobijamo diskontinuitet druge vrste, budući da je lim x → 0 - 0 x a \u003d - ∞, lim x → 0 + 0 x a \u003d + ∞ za a \u003d - 1, - 3, - 5, .... Dakle, prava linija x = 0 je vertikalna asimptota;

• raspon: y ∈ (- ∞ ; 0) ∪ (0 ; + ∞) ;
• funkcija je neparna jer y (- x) = - y (x) ;
• funkcija je opadajuća za x ∈ - ∞ ; 0 ∪ (0 ; + ∞) ;
• funkcija je konveksna za x ∈ (- ∞ ; 0) i konkavna za x ∈ (0 ; + ∞) ;
• nema pregibnih tačaka;

k = lim x → ∞ x a x = 0 , b = lim x → ∞ (x a - k x) = 0 ⇒ y = k x + b = 0 kada je a = - 1 , - 3 , - 5 , . . . .

• prolazne točke funkcije: (- 1 ; - 1) , (1 ; 1) .

Na slici ispod prikazani su primjeri grafova funkcije snage y = x a kada je a paran negativan broj: y = x - 8 (grafikon u crnoj boji); y = x - 4 (plava boja grafikona); y = x - 2 (crvena boja grafikona).

Definicija 9

Svojstva funkcije snage kada je eksponent čak negativan:

• domen definicije: x ∈ (- ∞ ; 0) ∪ (0 ; + ∞) ;

Kada je x = 0, dobijamo diskontinuitet druge vrste, budući da je lim x → 0 - 0 x a \u003d + ∞, lim x → 0 + 0 x a \u003d + ∞ za a \u003d - 2, - 4, - 6, .... Dakle, prava linija x = 0 je vertikalna asimptota;

• funkcija je parna jer je y (- x) = y (x) ;
• funkcija raste za x ∈ (- ∞ ; 0) i opada za x ∈ 0 ; +∞ ;
• funkcija je konkavna za x ∈ (- ∞ ; 0) ∪ (0 ; + ∞) ;
• nema pregibnih tačaka;
• horizontalna asimptota je prava linija y = 0 jer:

k = lim x → ∞ x a x = 0 , b = lim x → ∞ (x a - k x) = 0 ⇒ y = k x + b = 0 kada je a = - 2 , - 4 , - 6 , . . . .

• prolazne tačke funkcije: (- 1 ; 1) , (1 ; 1) .

Od samog početka obratite pažnju na sledeći aspekt: ​​u slučaju kada je a pozitivan razlomak sa neparnim nazivnikom, neki autori uzimaju interval - ∞ kao domen definicije ove funkcije stepena; + ∞ , uvjetujući da je eksponent a nesvodljiv razlomak. Trenutno, autori mnogih edukativnih publikacija o algebri i počecima analize NE DEFINIRAJU funkcije snage, gdje je eksponent razlomak s neparnim nazivnikom za negativne vrijednosti argumenta. Dalje ćemo se pridržavati upravo takvog stava: uzimamo skup [ 0 ; +∞) . Preporuka za učenike: saznajte u ovom trenutku stav nastavnika kako biste izbjegli nesuglasice.

Dakle, pogledajmo funkciju napajanja y = x a kada je eksponent racionalan ili iracionalan broj pod uslovom da je 0< a < 1 .

Ilustrirajmo grafovima funkcije snage y = x a kada je a = 11 12 (grafikon u crnoj boji); a = 5 7 (crvena boja grafikona); a = 1 3 (plava boja grafikona); a = 2 5 (zelena boja grafikona).

Ostale vrijednosti eksponenta a (pod pretpostavkom 0< a < 1) дадут аналогичный вид графика.

Definicija 10

Svojstva funkcije snage na 0< a < 1:

• opseg: y ∈ [ 0 ; +∞) ;
• funkcija raste za x ∈ [ 0 ; +∞) ;
• funkcija ima konveksnost za x ∈ (0 ; + ∞) ;
• nema pregibnih tačaka;
• nema asimptota;

Analizirajmo funkciju snage y = x a kada je eksponent necijeli racionalan ili iracionalan broj pod uslovom da je a > 1 .

Ilustrujemo grafove funkcije snage y = x a pod datim uslovima na primeru ovakvih funkcija: y = x 5 4 , y = x 4 3 , y = x 7 3 , y = x 3 π (crna, crvena, plava, zelena boja grafikona, respektivno) .

Druge vrijednosti eksponenta a pod uvjetom a > 1 dat će sličan prikaz grafa.

Definicija 11

Svojstva funkcije snage za a > 1:

• domen definicije: x ∈ [ 0 ; +∞) ;
• opseg: y ∈ [ 0 ; +∞) ;
• ova funkcija je funkcija opšteg oblika (nije ni neparna ni parna);
• funkcija raste za x ∈ [ 0 ; +∞) ;
• funkcija je konkavna za x ∈ (0 ; + ∞) (kada je 1< a < 2) и выпуклость при x ∈ [ 0 ; + ∞) (когда a > 2);
• nema pregibnih tačaka;
• nema asimptota;
• prolazne tačke funkcije: (0 ; 0) , (1 ; 1) .

Skrećemo vam pažnju: Kada je a negativan razlomak sa neparnim nazivnikom, u radovima nekih autora postoji stav da je domen definicije u ovom slučaju interval - ∞; 0 ∪ (0 ; + ∞) s tim da je eksponent a nesvodljiv razlomak. Trenutno autori nastavni materijali prema algebri i počecima analize, funkcije stepena s eksponentom u obliku razlomka s neparnim nazivnikom s negativnim vrijednostima argumenta NISU DEFINIRANE. Nadalje, pridržavamo se upravo takvog gledišta: uzimamo skup (0 ; + ∞) kao domenu funkcija stepena s razlomkom negativnih eksponenta. Prijedlog za učenike: U ovom trenutku razjasnite viziju svog nastavnika kako biste izbjegli neslaganje.

Nastavljamo temu i analiziramo funkciju snage y = x a predviđeno: - 1< a < 0 .

Evo crteža grafikona sljedeće karakteristike: y = x - 5 6 , y = x - 2 3 , y = x - 1 2 2 , y = x - 1 7 (crne, crvene, plave, zelene linije redom).

Definicija 12

Svojstva funkcije snage na -1< a < 0:

lim x → 0 + 0 x a = + ∞ kada je - 1< a < 0 , т.е. х = 0 – вертикальная асимптота;

• opseg: y ∈ 0 ; +∞ ;
• ova funkcija je funkcija opšteg oblika (nije ni neparna ni parna);
• nema pregibnih tačaka;

Crtež ispod prikazuje grafike funkcija stepena y = x - 5 4 , y = x - 5 3 , y = x - 6 , y = x - 24 7 (crna, crvena, plava, zelene boje krive).

Definicija 13

Svojstva funkcije snage za a< - 1:

• domen definicije: x ∈ 0 ; +∞ ;

lim x → 0 + 0 x a = + ∞ kada je a< - 1 , т.е. х = 0 – вертикальная асимптота;

• raspon: y ∈ (0 ; + ∞) ;
• ova funkcija je funkcija opšteg oblika (nije ni neparna ni parna);
• funkcija se smanjuje za x ∈ 0; +∞ ;
• funkcija je konkavna za x ∈ 0; +∞ ;
• nema pregibnih tačaka;
• horizontalna asimptota - prava linija y = 0 ;
• prolazna točka funkcije: (1 ; 1) .

Kada je a = 0 i x ≠ 0, dobijamo funkciju y = x 0 = 1, koja određuje liniju iz koje je isključena tačka (0; 1) (složili smo se da izraz 0 0 neće biti dat bilo koju vrijednost).

Eksponencijalna funkcija ima oblik y = a x , gdje je a > 0 i a ≠ 1 , a grafik ove funkcije izgleda drugačije na osnovu vrijednosti baze a . Razmotrimo posebne slučajeve.

Razmotrimo prvo situaciju kada je osnova eksponencijalna funkcija ima vrijednost od nula do jedan (0< a < 1) . Ilustrativan primjer su grafovi funkcija za a = 1 2 (plava boja krive) i a = 5 6 (crvena boja krive).

Grafovi eksponencijalne funkcije će imati sličan oblik za druge vrijednosti baze, pod uslovom da je 0< a < 1 .

Definicija 14

Svojstva eksponencijalne funkcije kada je baza manja od jedan:

• raspon: y ∈ (0 ; + ∞) ;
• ova funkcija je funkcija opšteg oblika (nije ni neparna ni parna);
• eksponencijalna funkcija čija je baza manja od jedan opada u cijelom domenu definicije;
• nema pregibnih tačaka;
• horizontalna asimptota je prava linija y = 0 sa varijablom x koja teži + ∞ ;

Sada razmotrite slučaj kada je baza eksponencijalne funkcije veća od jedan (a > 1).

Ilustrujmo ovaj poseban slučaj sa grafikom eksponencijalnih funkcija y = 3 2 x (plava boja krive) i y = e x (crvena boja grafika).

Druge vrijednosti baze, veće od jedan, dat će sličan prikaz grafa eksponencijalne funkcije.

Definicija 15

Svojstva eksponencijalne funkcije kada je baza veća od jedan:

• domen definicije je čitav skup realnih brojeva;
• raspon: y ∈ (0 ; + ∞) ;
• ova funkcija je funkcija opšteg oblika (nije ni neparna ni parna);
• eksponencijalna funkcija čija je baza veća od jedan raste za x ∈ - ∞ ; +∞ ;
• funkcija je konkavna za x ∈ - ∞ ; +∞ ;
• nema pregibnih tačaka;
• horizontalna asimptota - prava linija y = 0 sa promenljivom x koja teži - ∞ ;
• prolazna točka funkcije: (0 ; 1) .

Logaritamska funkcija ima oblik y = log a (x) , gdje je a > 0 , a ≠ 1 .

Takva funkcija je definirana samo za pozitivne vrijednosti argumenta: za x ∈ 0 ; +∞ .

Grafikon logaritamske funkcije ima drugačiji oblik, na osnovu vrijednosti baze a.

Razmotrimo prvo situaciju kada je 0< a < 1 . Продемонстрируем этот частный случай графиком логарифмической функции при a = 1 2 (синий цвет кривой) и а = 5 6 (красный цвет кривой).

Druge vrijednosti baze, ne veće od jedan, dat će sličan prikaz grafa.

Definicija 16

Svojstva logaritamske funkcije kada je baza manja od jedan:

• domen definicije: x ∈ 0 ; +∞ . Kako x teži nuli s desne strane, vrijednosti funkcije teže + ∞;
• raspon: y ∈ - ∞ ; +∞ ;
• ova funkcija je funkcija opšteg oblika (nije ni neparna ni parna);
• logaritamski
• funkcija je konkavna za x ∈ 0; +∞ ;
• nema pregibnih tačaka;
• nema asimptota;

Sada analizirajmo poseban slučaj kada je baza logaritamske funkcije veća od jedan: a > 1 . Na donjem crtežu se nalaze grafovi logaritamskih funkcija y = log 3 2 x i y = ln x (plava i crvena boja grafika, respektivno).

Druge vrijednosti baze veće od jedan će dati sličan prikaz grafa.

Definicija 17

Svojstva logaritamske funkcije kada je baza veća od jedan:

• domen definicije: x ∈ 0 ; +∞ . Kako x teži nuli s desne strane, vrijednosti funkcije teže - ∞;
• raspon: y ∈ - ∞ ; + ∞ (cijeli skup realnih brojeva);
• ova funkcija je funkcija opšteg oblika (nije ni neparna ni parna);
• logaritamska funkcija raste za x ∈ 0; +∞ ;
• funkcija ima konveksnost za x ∈ 0; +∞ ;
• nema pregibnih tačaka;
• nema asimptota;
• prolazna točka funkcije: (1 ; 0) .

Trigonometrijske funkcije su sinus, kosinus, tangent i kotangens. Analizirajmo svojstva svakog od njih i odgovarajuće grafove.

Općenito, sve trigonometrijske funkcije karakterizira svojstvo periodičnosti, tj. kada se vrijednosti funkcije ponavljaju na različita značenja argument, koji se međusobno razlikuju po vrijednosti perioda f (x + T) = f (x) (T je period). Tako se na listu svojstava trigonometrijskih funkcija dodaje stavka "najmanje pozitivno razdoblje". Osim toga, naznačit ćemo takve vrijednosti argumenta za koje odgovarajuća funkcija nestaje.

1. Sinusna funkcija: y = sin(x)

Grafikon ove funkcije naziva se sinusni val.

Definicija 18

Svojstva sinusne funkcije:

• domen definicije: cijeli skup realnih brojeva x ∈ - ∞ ; +∞ ;
• funkcija nestaje kada je x = π k , gdje je k ∈ Z (Z je skup cijelih brojeva);
• funkcija raste za x ∈ - π 2 + 2 π · k ; π 2 + 2 π k , k ∈ Z i opadajući za x ∈ π 2 + 2 π k ; 3 π 2 + 2 π k , k ∈ Z ;
• sinusna funkcija ima lokalni maksimumi u tačkama π 2 + 2 π · k ; 1 i lokalni minimumi u tačkama - π 2 + 2 π · k ; - 1 , k ∈ Z ;
• sinusna funkcija je konkavna kada je x ∈ - π + 2 π k; 2 π k , k ∈ Z i konveksan kada je x ∈ 2 π k ; π + 2 π k , k ∈ Z ;
• nema asimptota.

1. kosinus funkcija: y=cos(x)

Graf ove funkcije naziva se kosinusni val.

Definicija 19

Svojstva kosinusne funkcije:

• domen definicije: x ∈ - ∞ ; +∞ ;
• najmanji pozitivni period: T \u003d 2 π;
• raspon: y ∈ - 1 ; jedan ;
• ova funkcija je parna, budući da je y (- x) = y (x) ;
• funkcija raste za x ∈ - π + 2 π · k ; 2 π · k , k ∈ Z i opadajući za x ∈ 2 π · k ; π + 2 π k , k ∈ Z ;
• kosinusna funkcija ima lokalne maksimume u tačkama 2 π · k ; 1 , k ∈ Z i lokalni minimumi u tačkama π + 2 π · k ; - 1 , k ∈ z ;
• kosinusna funkcija je konkavna kada je x ∈ π 2 + 2 π · k ; 3 π 2 + 2 π k , k ∈ Z i konveksan kada je x ∈ - π 2 + 2 π k ; π 2 + 2 π · k , k ∈ Z ;
• tačke pregiba imaju koordinate π 2 + π · k ; 0 , k ∈ Z
• nema asimptota.

1. Tangentna funkcija: y = t g (x)

Poziva se graf ove funkcije tangentoid.

Definicija 20

Svojstva tangentne funkcije:

• domen definicije: x ∈ - π 2 + π · k ; π 2 + π k , gdje je k ∈ Z (Z je skup cijelih brojeva);
• Ponašanje tangentne funkcije na granici domene definicije lim x → π 2 + π · k + 0 t g (x) = - ∞ , lim x → π 2 + π · k - 0 t g (x) = + ∞ . Dakle, prave x = π 2 + π · k k ∈ Z su vertikalne asimptote;
• funkcija nestaje kada je x = π k za k ∈ Z (Z je skup cijelih brojeva);
• raspon: y ∈ - ∞ ; +∞ ;
• ova funkcija je neparna jer y (- x) = - y (x) ;
• funkcija raste na - π 2 + π · k ; π 2 + π k , k ∈ Z ;
• tangentna funkcija je konkavna za x ∈ [ π · k ; π 2 + π k) , k ∈ Z i konveksan za x ∈ (- π 2 + π k ; π k ] , k ∈ Z ;
• tačke pregiba imaju koordinate π k; 0 , k ∈ Z ;

1. Kotangens funkcija: y = c t g (x)

Graf ove funkcije naziva se kotangentoid. .

Definicija 21

Svojstva kotangens funkcije:

• domen definicije: x ∈ (π k ; π + π k) , gdje je k ∈ Z (Z je skup cijelih brojeva);

Ponašanje kotangensne funkcije na granici domene definicije lim x → π · k + 0 t g (x) = + ∞ , lim x → π · k - 0 t g (x) = - ∞ . Dakle, prave x = π k k ∈ Z su vertikalne asimptote;

• najmanji pozitivni period: T \u003d π;
• funkcija nestaje kada je x = π 2 + π k za k ∈ Z (Z je skup cijelih brojeva);
• raspon: y ∈ - ∞ ; +∞ ;
• ova funkcija je neparna jer y (- x) = - y (x) ;
• funkcija je opadajuća za x ∈ π · k ; π + π k , k ∈ Z ;
• kotangensna funkcija je konkavna za x ∈ (π k ; π 2 + π k ], k ∈ Z i konveksna za x ∈ [ - π 2 + π k ; π k) , k ∈ Z ;
• tačke pregiba imaju koordinate π 2 + π · k ; 0 , k ∈ Z ;
• nema kosih i horizontalnih asimptota.

Inverzne trigonometrijske funkcije su arksinus, arkosinus, arktangens i arkkotangens. Često se, zbog prisustva prefiksa "luk" u nazivu, inverzne trigonometrijske funkcije nazivaju lučne funkcije. .

1. Arksinus funkcija: y = a r c sin (x)

Definicija 22

Svojstva arcsinusne funkcije:

• ova funkcija je neparna jer y (- x) = - y (x) ;
• arcsinusna funkcija je konkavna za x ∈ 0; 1 i konveksnost za x ∈ - 1 ; 0;
• tačke pregiba imaju koordinate (0 ; 0) , to je i nula funkcije;
• nema asimptota.

1. Arkosinus funkcija: y = a r c cos (x)

Definicija 23

Svojstva arkosinusne funkcije:

• domen definicije: x ∈ - 1 ; jedan ;
• opseg: y ∈ 0 ; π;
• ova funkcija je opšteg oblika (ni parna ni neparna);
• funkcija se smanjuje na cijelom domenu definicije;
• arkosinusna funkcija je konkavna za x ∈ - 1 ; 0 i konveksnost za x ∈ 0 ; jedan ;
• tačke pregiba imaju koordinate 0 ; π2;
• nema asimptota.

1. Arktangentna funkcija: y = a r c t g (x)

Definicija 24

Svojstva arktangentne funkcije:

• domen definicije: x ∈ - ∞ ; +∞ ;
• opseg: y ∈ - π 2 ; π2;
• ova funkcija je neparna jer y (- x) = - y (x) ;
• funkcija se povećava u cijelom domenu definicije;
• arktangentna funkcija je konkavna za x ∈ (- ∞ ; 0 ] i konveksna za x ∈ [ 0 ; + ∞) ;
• tačka pregiba ima koordinate (0; 0), ona je i nula funkcije;
• horizontalne asimptote su prave linije y = - π 2 za x → - ∞ i y = π 2 za x → + ∞ (asimptote na slici su zelene linije).

1. Kotangentna funkcija luka: y = a r c c t g (x)

Definicija 25

Svojstva funkcije kotangensa luka:

• domen definicije: x ∈ - ∞ ; +∞ ;
• opseg: y ∈ (0 ; π) ;
• ova funkcija je opšteg tipa;
• funkcija se smanjuje na cijelom domenu definicije;
• arc kotangens funkcija je konkavna za x ∈ [ 0 ; + ∞) i konveksnost za x ∈ (- ∞ ; 0 ] ;
• tačka pregiba ima koordinate 0 ; π2;
• horizontalne asimptote su prave linije y = π na x → - ∞ (zelena linija na crtežu) i y = 0 pri x → + ∞.

Ako primijetite grešku u tekstu, označite je i pritisnite Ctrl+Enter

Funkcija napajanja. Ovo je funkcija: y = ax n, gdje a,n- trajno. At n= 1 dobijamo direktna proporcionalnost: y = sjekira; at n = 2 - kvadratna parabola ; at n = - 1 - inverzna proporcionalnost ili hiperbola. Dakle, ove funkcije su posebni slučajevi funkcije moći. Znamo da je nulta snaga svakog broja različitog od nule 1, dakle, u n= 0 funkcija snage postaje konstanta:y = a, tj. e. njen raspored je duž, osa paralelna X, isključujući porijeklo (pojasni molim te, zašto? ). Svi ovi slučajevi (sa a= 1 ) prikazano na sl.13 (n 0 ) i sl.14 ( n < 0). Отрицательные значения xse ovdje ne razmatraju kao onda neke funkcije:

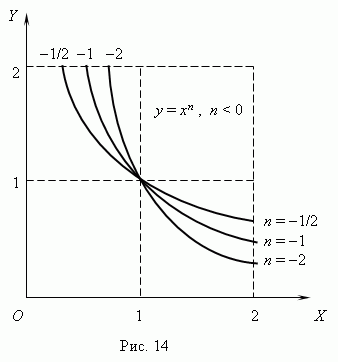
Ako a n– cijele, funkcije snage imaju smisla čak i kadax< 0, но их графики имеют различный вид в зависимости от того, является ли nparan ili neparan broj. Slika 15 prikazuje dvije takve funkcije snage: za n= 2 i n = 3.


At n= 2 funkcija je parna injegov graf je simetričan oko ose Y. At n= 3 funkcija je neparna i njen graf je simetričan u odnosu na ishodište koordinate. Funkcijay = x 3 pozvao kubna parabola.

Slika 16 prikazuje funkciju . Ovo funkcija je inverzna kvadratnoj paraboli y = x 2 , njegov graf se dobija rotacijom grafa kvadratna parabola oko simetrale 1. koordinatnog ugla. Ovo je način da dobijete grafikon bilo kojeg inverzna funkcija iz grafa njegove originalne funkcije. Iz grafikona možemo vidjeti da se radi o funkciji s dvije vrijednosti (ovo je također označeno znakom ± ispred kvadratni korijen). Takve funkcije se ne proučavaju u elementarnoj matematici, pa kao funkciju obično razmatramo jednu od njenih grana: gornju ili donju.

Prvo pokušajte pronaći opseg funkcije:

Jeste li uspjeli? Uporedimo odgovore:

U redu? Dobro urađeno!

Pokušajmo sada pronaći raspon funkcije:

Pronađen? uporedi:

Je li se složilo? Dobro urađeno!

Idemo opet raditi s grafovima, samo što je sada malo teže - pronaći i domenu funkcije i opseg funkcije.

Kako pronaći i domenu i opseg funkcije (napredno)

Evo šta se dogodilo:

Što se tiče grafike, mislim da ste shvatili. Pokušajmo sada pronaći domenu funkcije u skladu s formulama (ako ne znate kako to učiniti, pročitajte odjeljak o):

Jeste li uspjeli? Provjeravam odgovori:

1. , budući da korijenski izraz mora biti veći ili jednak nuli.
2. , budući da je nemoguće podijeliti sa nulom i radikalni izraz ne može biti negativan.
3. , pošto, respektivno, za sve.
4. jer ne možete podijeliti sa nulom.

Ipak, ostaje nam još jedan trenutak koji nije sređen...

Dozvolite mi da ponovim definiciju i da se fokusiram na nju:

Primijećeno? Riječ "samo" je vrlo, vrlo važan element naše definicije. Pokušaću da ti na prste objasnim.

Recimo da imamo funkciju datu pravom linijom. . Kada, ovu vrijednost zamjenjujemo u naše "pravilo" i dobijamo to. Jedna vrijednost odgovara jednoj vrijednosti. Možemo čak napraviti tablicu različitih vrijednosti i nacrtati datu funkciju da to potvrdimo.

„Pogledaj! - kažete, - "" sastaje se dvaput!" Dakle, možda parabola nije funkcija? Ne, jeste!

Činjenica da se "" pojavljuje dva puta daleko je od razloga da se parabola optužuje za dvosmislenost!

Činjenica je da smo, računajući za, dobili jednu utakmicu. I kada se računa sa, dobili smo jednu utakmicu. Tako je, parabola je funkcija. Pogledajte grafikon:

Jasno? Ako ne, evo vam primjera iz stvarnog života, daleko od matematike!

Recimo da imamo grupu aplikanata koji su se sreli prilikom podnošenja dokumenata, od kojih je svaki u razgovoru rekao gdje živi:

Slažem se, sasvim je realno da nekoliko momaka živi u istom gradu, ali nemoguće je da jedna osoba živi u više gradova u isto vrijeme. Ovo je, takoreći, logičan prikaz naše "parabole" - Nekoliko različitih x odgovara istom y.

Hajde sada da smislimo primjer gdje ovisnost nije funkcija. Recimo da su ti isti momci ispričali za koje su se specijalnosti prijavili:

Ovdje imamo potpuno drugačiju situaciju: jedna osoba se lako može prijaviti za jedan ili više smjerova. tj jedan element setovi se dopisuju više elemenata setovi. odnosno to nije funkcija.

Provjerimo svoje znanje u praksi.

Odredite iz slika što je funkcija, a što nije:

Jasno? I evo ga odgovori:

• Funkcija je - B,E.
• Nije funkcija - A, B, D, D.

Pitate zašto? Da, evo zašto:

U svim brojkama osim AT) i E) ima ih nekoliko za jednog!

Siguran sam da sada možete lako razlikovati funkciju od ne-funkcije, reći šta je argument, a šta zavisna varijabla, kao i odrediti opseg argumenta i opseg funkcije. Pređimo na sljedeći odjeljak - kako definirati funkciju?

Načini postavljanja funkcije

Šta mislite šta znače riječi "postavi funkciju"? Tako je, znači objasniti svima o kojoj funkciji je riječ u ovom slučaju. Štaviše, objasnite na način da vas svi dobro razumiju i da su grafovi funkcija koje su ljudi nacrtali prema vašem objašnjenju bili isti.

Kako to mogu učiniti? Kako postaviti funkciju? Najlakši način, koji je već korišten više puta u ovom članku - koristeći formulu. Pišemo formulu i zamjenom vrijednosti u nju izračunavamo vrijednost. I kao što se sjećate, formula je zakon, pravilo prema kojem nama i drugoj osobi postaje jasno kako se X pretvara u Y.

Obično upravo to rade - u zadacima vidimo gotove funkcije definirane formulama, međutim, postoje i drugi načini postavljanja funkcije na koje svi zaboravljaju, a samim tim i pitanje "kako drugačije možete postaviti funkciju?" zbunjuje. Pogledajmo sve redom i počnimo s analitičkom metodom.

Analitički način definiranja funkcije

Analitička metoda je zadatak funkcije koja koristi formulu. Ovo je najuniverzalniji i najsveobuhvatniji i nedvosmislen način. Ako imate formulu, onda znate apsolutno sve o funkciji - možete napraviti tablicu vrijednosti ​​na njoj, možete napraviti graf, odrediti gdje se funkcija povećava, a gdje smanjuje, općenito, istražite je u cijelosti.

Razmotrimo funkciju. šta to ima veze?

"Šta to znači?" - pitate. Sad ću objasniti.

Da vas podsjetim da se u notaciji izraz u zagradama naziva argumentom. A ovaj argument može biti bilo koji izraz, ne nužno jednostavan. Prema tome, bez obzira na argument (izraz u zagradama), umjesto toga ćemo ga napisati u izrazu.

U našem primjeru to će izgledati ovako:

Razmotrite još jedan zadatak koji se odnosi na analitičku metodu specificiranja funkcije koju ćete imati na ispitu.

Pronađite vrijednost izraza, at.

Sigurna sam da ste se u početku uplašili kada ste vidjeli takav izraz lica, ali u tome nema apsolutno ničeg strašnog!

Sve je isto kao u prethodnom primjeru: bez obzira na argument (izraz u zagradama), umjesto toga ćemo ga napisati u izrazu. Na primjer, za funkciju.

Šta bi trebalo učiniti u našem primjeru? Umjesto toga, trebate napisati, a umjesto -:

skratiti rezultirajući izraz:

To je sve!

Samostalan rad

Sada pokušajte sami pronaći značenje sljedećih izraza:

1. , ako
2. , ako

Jeste li uspjeli? Uporedimo naše odgovore: Navikli smo na činjenicu da funkcija ima oblik

Čak iu našim primjerima funkciju definiramo na ovaj način, ali je analitički moguće definirati funkciju implicitno, na primjer.

Pokušajte sami izgraditi ovu funkciju.

Jeste li uspjeli?

Evo kako sam ga napravio.

Sa kojom smo jednačinom dobili?

Ispravno! Linearno, što znači da će graf biti prava linija. Napravimo tabelu da odredimo koje tačke pripadaju našoj liniji:

Upravo o tome smo pričali... Jedan odgovara nekoliko.

Hajde da pokušamo da nacrtamo šta se desilo:

Je li ono što imamo funkcija?

Tako je, ne! Zašto? Pokušajte odgovoriti na ovo pitanje slikom. šta si dobio?

“Zato što jedna vrijednost odgovara nekoliko vrijednosti!”

Kakav zaključak možemo izvući iz ovoga?

Tako je, funkcija se ne može uvijek eksplicitno izraziti, a ono što je "prikriveno" u funkciju nije uvijek funkcija!

Tabelarni način definiranja funkcije

Kao što ime govori, ova metoda je jednostavna ploča. Da da. Kao onaj koji smo već napravili. Na primjer:

Ovdje ste odmah primijetili uzorak - Y je tri puta veći od X. A sada zadatak „vrlo dobro razmislite“: mislite li da je funkcija data u obliku tabele ekvivalentna funkciji?

Hajde da ne pričamo dugo, nego da crtamo!

Dakle. Crtamo funkciju datu na oba načina:

Vidite li razliku? Ne radi se o označenim tačkama! Pogledajte izbliza:

Jeste li ga sada vidjeli? Kada funkciju postavimo na tabelarni način, na grafu odražavamo samo one tačke koje imamo u tabeli i linija (kao u našem slučaju) prolazi samo kroz njih. Kada definiramo funkciju na analitički način, možemo uzeti bilo koje točke, a naša funkcija nije ograničena na njih. Evo takve karakteristike. Zapamtite!

Grafički način za izgradnju funkcije

Grafički način konstrukcija funkcije nije ništa manje zgodna. Nacrtamo našu funkciju, a druga zainteresirana osoba može pronaći koliko je y jednako pri određenom x, i tako dalje. Grafičke i analitičke metode su među najčešćim.

Međutim, ovdje se morate sjetiti o čemu smo pričali na samom početku - nije svaka „švergla“ nacrtana u koordinatnom sistemu funkcija! Zapamtite? Za svaki slučaj, kopiraću ovde definiciju šta je funkcija:

U pravilu ljudi obično imenuju upravo ona tri načina definiranja funkcije koja smo analizirali - analitički (pomoću formule), tabelarni i grafički, potpuno zaboravljajući da se funkcija može opisati verbalno. Volim ovo? Da, vrlo lako!

Verbalni opis funkcije

Kako verbalno opisati funkciju? Uzmimo naš nedavni primjer - . Ova funkcija može se opisati kao "svaka realna vrijednost x odgovara njegovoj trostrukoj vrijednosti". To je sve. Ništa komplikovano. Naravno, prigovorit ćete - "postoje tako složene funkcije koje je jednostavno nemoguće verbalno postaviti!" Da, ima ih, ali postoje funkcije koje je lakše opisati verbalno nego postaviti formulom. Na primjer: "svaka prirodna vrijednost x odgovara razlici između cifara od kojih se sastoji, dok se najveća cifra sadržana u unosu broja uzima kao minus." Sada razmotrite kako se naš verbalni opis funkcije implementira u praksi:

Najveća znamenka u datom broju - odnosno - se smanjuje, tada:

Glavne vrste funkcija

Sada pređimo na ono najzanimljivije - razmotrit ćemo glavne vrste funkcija s kojima ste radili/radili i radit ćete u toku školske i institutske matematike, odnosno upoznaćemo ih, da tako kažem, i daj im kratak opis. Pročitajte više o svakoj funkciji u odgovarajućem odjeljku.

Linearna funkcija

Funkcija oblika, gdje su realni brojevi.

Grafikon ove funkcije je prava linija, dakle konstrukcija linearna funkcija svodi se na pronalaženje koordinata dvije tačke.

Direktna pozicija na koordinatnu ravan zavisi od faktora nagiba.

Opseg funkcije (aka raspon argumenata) - .

Raspon vrijednosti je .

kvadratna funkcija

Funkcija forme, gdje

Graf funkcije je parabola, kada su grane parabole usmjerene prema dolje, kada - prema gore.

Mnoge nekretnine kvadratna funkcija zavisi od vrednosti diskriminanta. Diskriminanta se izračunava po formuli

Položaj parabole na koordinatnoj ravni u odnosu na vrijednost i koeficijent prikazan je na slici:

Domain

Raspon vrijednosti ovisi o ekstremumu date funkcije (vrh parabole) i koeficijentu (smjer grana parabole)

Inverzna proporcionalnost

Funkcija data formulom, gdje

Broj se naziva faktor inverzne proporcionalnosti. Ovisno o kojoj vrijednosti, grane hiperbole su u različitim kvadratima:

Domena - .

Raspon vrijednosti je .

SAŽETAK I OSNOVNA FORMULA

1. Funkcija je pravilo prema kojem se svakom elementu skupa dodjeljuje jedinstveni element skupa.

• - ovo je formula koja označava funkciju, odnosno zavisnost jedne varijable od druge;
• - varijabla ili argument;
• - zavisna vrijednost - mijenja se kada se argument promijeni, odnosno prema nekima određene formule, što odražava zavisnost jedne veličine od druge.

2. Važeće vrijednosti argumenata, ili opseg funkcije, je ono što je povezano s mogućim pod kojim funkcija ima smisla.

3. Raspon vrijednosti funkcije- to su vrijednosti koje uzima, sa važećim vrijednostima.

4. Postoje 4 načina za postavljanje funkcije:

• analitički (koristeći formule);
• tabelarni;
• grafički
• verbalni opis.

5. Glavne vrste funkcija:

• : , gdje su realni brojevi;
• : , gdje;
• : , gdje.

Nacionalni istraživački univerzitet

Katedra za primijenjenu geologiju

Abstract on višu matematiku

Na temu: "Osnovne elementarne funkcije,

njihova svojstva i grafikoni"

Završeno:

Provjereno:

nastavnik

Definicija. Funkcija data formulom y=a x (gdje je a>0, a≠1) naziva se eksponencijalna funkcija s bazom a.

Hajde da formulišemo glavna svojstva eksponencijalne funkcije:

1. Područje definicije je skup (R) svih realnih brojeva.

2. Raspon vrijednosti je skup (R+) svih pozitivnih realnih brojeva.

3. Kada je a > 1, funkcija raste na cijeloj realnoj liniji; u 0<а<1 функция убывает.

4. Opća je funkcija.

, na intervalu xO [-3;3] , na intervalu xO [-3;3]

Funkcija oblika y(h)=h n, gdje je n broj ILI, naziva se funkcija stepena. Broj n može poprimiti različite vrijednosti: i cijeli i razlomak, paran i neparan. Ovisno o tome, funkcija snage će imati drugačiji oblik. Razmotrimo posebne slučajeve koji su funkcije stepena i odražavaju glavna svojstva ove vrste krivulja sljedećim redoslijedom: funkcija snage y = x² (funkcija s parnim eksponentom - parabola), funkcija snage y = x³ (funkcija s neparnim eksponentom - kubnom parabolom) i funkcijom y \u003d √ x (x na stepen ½) (funkcija s razlomkom), funkcija s negativnim cjelobrojnim eksponentom (hiperbola).

Funkcija napajanja y=x²

1. D(x)=R – funkcija je definirana na cijeloj numeričkoj osi;

2. E(y)= i raste na intervalu

Funkcija napajanja y=x³

1. Graf funkcije y \u003d x³ naziva se kubna parabola. Funkcija snage y=x³ ima sljedeća svojstva:

2. D(x)=R – funkcija je definirana na cijeloj numeričkoj osi;

3. E(y)=(-∞;∞) – funkcija preuzima sve vrijednosti u svojoj domeni definicije;

4. Kada je x=0 y=0 – funkcija prolazi kroz ishodište O(0;0).

5. Funkcija se povećava u cijelom domenu definicije.

6. Funkcija je neparna (simetrična u odnosu na ishodište).

, na intervalu xn [-3;3]

U zavisnosti od brojčanog faktora ispred x³, funkcija može biti strma / ravna i povećava se / smanjuje.

Funkcija snage s cijelim negativnim eksponentom:

Ako je eksponent n neparan, tada se graf takve funkcije stepena naziva hiperbola. Funkcija stepena s negativnim cijelim eksponentom ima sljedeća svojstva:

1. D(x)=(-∞;0)U(0;∞) za bilo koje n;

2. E(y)=(-∞;0)U(0;∞) ako je n neparan broj; E(y)=(0;∞) ako je n paran broj;

3. Funkcija se smanjuje u cijeloj domeni definicije ako je n neparan broj; funkcija raste na intervalu (-∞;0) i opada na intervalu (0;∞) ako je n paran broj.

4. Funkcija je neparna (simetrična u odnosu na ishodište) ako je n neparan broj; funkcija je parna ako je n paran broj.

5. Funkcija prolazi kroz tačke (1;1) i (-1;-1) ako je n neparan broj i kroz tačke (1;1) i (-1;1) ako je n paran broj.

, na intervalu xn [-3;3]

Funkcija stepena s razlomkom eksponenta

Funkcija stepena sa frakcijskim eksponentom oblika (slika) ima graf funkcije prikazane na slici. Funkcija stepena s razlomkom eksponenta ima sljedeća svojstva: (slika)

1. D(x) ILI, ako je n neparan broj i D(x)= , na intervalu xO , na intervalu xO [-3;3]

Logaritamska funkcija y \u003d log a x ima sljedeća svojstva:

1. Područje definicije D(x)n (0; + ∞).

2. Raspon vrijednosti E(y) O (- ∞; + ∞)

3. Funkcija nije ni parna ni neparna (općenito).

4. Funkcija raste na intervalu (0; + ∞) za a > 1, opada na (0; + ∞) za 0< а < 1.

Graf funkcije y = log a x može se dobiti iz grafa funkcije y = a x korištenjem simetrijske transformacije oko prave y = x. Na slici 9 je prikazan dijagram logaritamske funkcije za a > 1, a na slici 10 - za 0< a < 1.

; na intervalu xn ; na intervalu xO

Funkcije y = sin x, y = cos x, y = tg x, y = ctg x nazivaju se trigonometrijske funkcije.

Funkcije y = sin x, y = tg x, y = ctg x su neparne, a funkcija y = cos x je parna.

Funkcija y \u003d sin (x).

1. Područje definicije D(x) ILI.

2. Raspon vrijednosti E(y) O [ - 1; jedan].

3. Funkcija je periodična; glavni period je 2π.

4. Funkcija je neparna.

5. Funkcija raste na intervalima [ -π/2 + 2πn; π/2 + 2πn] i opada na intervalima [ π/2 + 2πn; 3π/2 + 2πn], n O Z.

Grafikon funkcije y = sin (x) prikazan je na slici 11.