tema :

Target : Formirati ideju o derivatima inverza trigonometrijske funkcije.

Zadaci:

1. naučiti pronaći izvode ovih funkcija,razraditi sa učenicima sposobnost razlikovanja ovih funkcija koristeći
samostalan rad i međusobna provjera;

2. razviti interesovanje za matematiku, računarstvo i kognitivni vještine,
sposobnost analiziranja grešaka drugih učenika;

3. neguju svesnost, nezavisnost

1. Organizacioni momenat
Pozdravljam učenike, upoznajem ih sa pravilima rada na času, objašnjavam kako pravilno popuniti bodovni list
2.Motivaciona faza
Učenici čitaju šta treba da znaju i umeju da urade na temu.
Prije nego što počnete, pročitajte pravilo ZAPAMTITE.
3. Operativna faza
Učenici popunjavaju nastavni list (u prilogu)
4. Sažetak lekcije
Refleksija.

Danas na nastavi:

saznao sam…

Bilo je zanimljivo…

Bilo je teško…

uspio sam…

Pokušat ću…

LEARNING LIST

na ovu temu: Derivati trigonometrijskih i inverznih trigonometrijskih funkcija.

2 lekcije.

KAO REZULTAT PROUČAVANJA TEME JE POTREBAN

ZNATI: formule diferencijacije za trigonometrijske i inverzne trigonometrijske funkcije.

MOĆI: naći izvode trigonometrijskih i inverznih trigonometrijskih funkcija.

zapamti , da algoritam treba da radi.

Ne zaboravite položiti test, napraviti bilješke na marginama, popuniti ocjenu teme.

Molimo ne ostavljajte pitanja na koja imate bez odgovora.

Budite objektivni tokom evaluacije, to će pomoći i vama i osobi koju provjeravate.

ŽELI VAM USPEH!

W ADANIE №1

Pročitajte i naučite formule za razlikovanje inverznih trigonometrijskih funkcija: (2 str.)

Ako je funkcija složena, onda

gdje z – elementarna funkcija

Razmotrimo primjere:

y=arcsin(x) zatim y/=

y = arcctg(3x 2 -4) onda

y/=

Pronađite derivate:(3 str.)

y= arcsin(-x) y= arctg(-x) y= arcos(2x)

P IDI PROVJERI №1

W ADANIE №2

Riješite bilo koji od primjera: (3b)

ali ) y = arcos(5x - 3)

b ) y = arcctg(7x+1)

P IDI PROVJERI №2

W ADANIE №3

a) Razmotrimo ponovo rješenje primjera:

b) Pronađite izvode funkcija (4 str.)

arcsin (2x 2 - 5x)

arccos (4x 2 - 6x)

P IDI PROVJERI №3

W ADANIE №4

Dobro urađeno! Možete početiverifikacioni rad broj 1.

ZADATAK #5

a) Razmotrimo rješenje primjera:

b) Pronađite izvode funkcija (6 str.)

P IDI PROVJERI №5

Dobro urađeno! Možete početiverifikacioni rad broj 2.

VERIFIKACIJSKI RAD №1

Uradite jednu od opcija (11b)

1v 2v

1. Pronađite derivate sljedeće funkcije:

a) 2 boda

y = arctg(-2x) y = arccos(3x)

b) 4 boda

y = arcos(3x 2 - 2) y = arcctg(2x 3 +1)

c) 5 bodova

y = arcsin(x 2 - 5x) + tan (2x+1) y = arccos(3x 2 - 2x) + ctg(x+4) max

bodova

primljeno

rezultat

SZO

provjereno

razred

2 b

3 b

1 1 b

6 b

1 4 b

ukupno

43 b

UKUPNO 43 boda

"5" - 33 - 43 boda;

"4" - 24 - 32 boda;

"3" - 18 - 23 poena.

Evo tabele sažetka za praktičnost i jasnoću prilikom proučavanja teme.

Konstantnoy=C

Funkcija snage y = x p

(x p)" = p x p - 1

Eksponencijalna funkcijay = x

(a x)" = a x ln a

Konkretno, kadaa = eimamo y = e x

(e x)" = e x

logaritamska funkcija

(log a x) " = 1 x ln a

Konkretno, kadaa = eimamo y = log x

(ln x)" = 1 x

Trigonometrijske funkcije

(sin x) "= cos x (cos x)" = - sin x (t g x) " = 1 cos 2 x (c t g x)" = - 1 sin 2 x

Inverzne trigonometrijske funkcije

(a r c sin x) " = 1 1 - x 2 (a r c cos x) " = - 1 1 - x 2 (a r c t g x) " = 1 1 + x 2 (a r c c t g x) " = - 1 1 + x 2

Hiperboličke funkcije

(s h x) " = c h x (c h x) " = s h x (t h x) " = 1 c h 2 x (c t h x) " = - 1 s h 2 x

Hajde da analiziramo kako su dobijene formule navedene tabele, odnosno dokazaćemo izvođenje formula za izvode za svaku vrstu funkcije.

Derivat konstante

Dokaz 1

Da bismo izveli ovu formulu, uzimamo kao osnovu definiciju derivacije funkcije u tački. Koristimo x 0 = x, gdje x poprima vrijednost bilo kojeg realnog broja, ili, drugim riječima, x je bilo koji broj iz domene funkcije f (x) = C . Zapišimo granicu omjera prirasta funkcije i priraštaja argumenta kao ∆ x → 0:

lim ∆ x → 0 ∆ f (x) ∆ x = lim ∆ x → 0 C - C ∆ x = lim ∆ x → 0 0 ∆ x = 0

Imajte na umu da izraz 0 ∆ x spada pod granični znak. To nije neodređenost “nule podijeljene sa nulom”, jer brojnik ne sadrži beskonačno mala vrijednost, odnosno nula. Drugim riječima, prirast konstantne funkcije je uvijek nula.

Dakle, derivacija konstantne funkcije f (x) = C jednaka je nuli u cijeloj domeni definicije.

Primjer 1

Zadate konstantne funkcije:

f 1 (x) = 3 , f 2 (x) = a , a ∈ R , f 3 (x) = 4 . 13 7 22 , f 4 (x) = 0 , f 5 (x) = - 8 7

Rješenje

Hajde da opišemo date uslove. U prvoj funkciji vidimo izvod prirodnog broja 3. U sljedećem primjeru morate uzeti derivat od ali, gdje ali- bilo koji pravi broj. Treći primjer nam daje derivat iracionalan broj 4 . 13 7 22 , četvrti - derivacija nule (nula je cijeli broj). Konačno, u petom slučaju imamo izvod racionalnog razlomka - 8 7 .

odgovor: derivati postaviti funkcije je nula za bilo koju realnu x(preko cijelog domena definicije)

f 1 " (x) = (3) " = 0 , f 2 " (x) = (a) " = 0 , a ∈ R , f 3 " (x) = 4 . 13 7 22 " = 0 , f 4 " (x) = 0 " = 0 , f 5 " (x) = - 8 7 " = 0

Derivat funkcije moći

Idemo dalje funkcija snage i formula njegovog izvoda, koji ima oblik: (x p) " = p x p - 1, gdje je eksponent str je bilo koji realan broj.

Dokaz 2

Predstavljamo dokaz formule kada je eksponent prirodni broj: p = 1 , 2 , 3 , …

Ponovo se oslanjamo na definiciju derivata. Napišimo granicu omjera prirasta funkcije snage i prirasta argumenta:

(x p) " = lim ∆ x → 0 = ∆ (x p) ∆ x = lim ∆ x → 0 (x + ∆ x) p - x p ∆ x

Da bismo pojednostavili izraz u brojiocu, koristimo Newtonovu binomnu formulu:

(x + ∆ x) p - x p = C p 0 + x p + C p 1 x p - 1 ∆ x + C p 2 x p - 2 (∆ x) 2 + . . . + + C pp - 1 x (∆ x) p - 1 + C pp (∆ x) p - xp = = C p 1 xp - 1 ∆ x + C p 2 xp - 2 (∆ x) 2 + . . . + C p p - 1 x (∆ x) p - 1 + C p p (∆ x) p

Na ovaj način:

(xp) " = lim ∆ x → 0 ∆ (xp) ∆ x = lim ∆ x → 0 (x + ∆ x) p - xp ∆ x = = lim ∆ x → 0 (C p 1 xp - 1 ∆ x + C p 2 xp - 2 (∆ x) 2 + . . . + C pp - 1 x (∆ x) p - 1 + C pp (∆ x) p) ∆ x = = lim ∆ x → 0 (C p 1 xp - 1 + C p 2 xp - 2 ∆ x + . . . + C pp - 1 x (∆ x) p - 2 + C pp (∆ x) p - 1) = = C p 1 xp - 1 + 0 + 0 + . . . + 0 = p! 1! (p - 1)! xp - 1 = p xp - 1

Dakle, dokazali smo formulu za izvod funkcije stepena kada je eksponent prirodan broj.

Dokaz 3

Da dam dokaz za slučaj kada p- bilo kojeg realnog broja osim nule, koristimo logaritamski izvod (ovdje treba razumjeti razliku od izvoda logaritamske funkcije). Za potpunije razumijevanje poželjno je proučiti izvod logaritamske funkcije i dodatno se pozabaviti derivacijom implicitno zadane funkcije i izvodom složena funkcija.

Razmotrimo dva slučaja: kada x pozitivno i kada x su negativni.

Dakle, x > 0 . Tada je: x p > 0 . Uzimamo logaritam jednakosti y \u003d x p na bazu e i primjenjujemo svojstvo logaritma:

y = x p ln y = ln x p ln y = p ln x

U ovoj fazi je dobijena implicitno definirana funkcija. Definirajmo njegovu derivaciju:

(ln y) " = (p ln x) 1 y y " = p 1 x ⇒ y " = p y x = p x p x = p x p - 1

Sada razmatramo slučaj kada x- negativan broj.

Ako indikator str je paran broj, tada je funkcija stepena također definirana za x< 0 , причем является четной: y (x) = - y ((- x) p) " = - p · (- x) p - 1 · (- x) " = = p · (- x) p - 1 = p · x p - 1

Zatim xp< 0 и возможно составить доказательство, используя логарифмическую производную.

Ako str je neparan broj, tada je funkcija stepena definirana za x< 0 , причем является нечетной: y (x) = - y (- x) = - (- x) p . Тогда x p < 0 , а значит логарифмическую производную задействовать нельзя. В такой ситуации возможно взять за основу доказательства правила дифференцирования и правило нахождения производной сложной функции:

y "(x) \u003d (- (- x) p) " \u003d - ((- x) p) " \u003d - p (- x) p - 1 (- x) " = \u003d p (- x ) p - 1 = p xp - 1

Posljednji prijelaz je moguć jer ako str je onda neparan broj p - 1 bilo paran broj ili nula (za p = 1), dakle, za negativan x jednakost (- x) p - 1 = x p - 1 je tačna.

Dakle, dokazali smo formulu za izvod funkcije stepena za bilo koje realno p.

Primjer 2

Zadate funkcije:

f 1 (x) = 1 x 2 3 , f 2 (x) = x 2 - 1 4 , f 3 (x) = 1 x log 7 12

Odredite njihove derivate.

Rješenje

Dio datih funkcija transformiramo u tabelarni oblik y = x p , na osnovu svojstava stepena, a zatim koristimo formulu:

f 1 (x) \u003d 1 x 2 3 \u003d x - 2 3 ⇒ f 1 "(x) \u003d - 2 3 x - 2 3 - 1 \u003d - 2 3 x - 5 3 f 2 "(x) \u003d x 2 - 1 4 = 2 - 1 4 x 2 - 1 4 - 1 = 2 - 1 4 x 2 - 5 4 f 3 (x) = 1 x log 7 12 = x - log 7 12 ⇒ f 3 " ( x) = - log 7 12 x - log 7 12 - 1 = - log 7 12 x - log 7 12 - log 7 7 = - log 7 12 x - log 7 84

Derivat eksponencijalne funkcije

Dokaz 4

Izvodimo formulu za izvod, na osnovu definicije:

(ax) " = lim ∆ x → 0 ax + ∆ x - ax ∆ x = lim ∆ x → 0 ax (a ∆ x - 1) ∆ x = ax lim ∆ x → 0 a ∆ x - 1 ∆ x = 0 0

Imamo neizvjesnost. Da bismo ga proširili, pišemo novu varijablu z = a ∆ x - 1 (z → 0 kao ∆ x → 0). U ovom slučaju a ∆ x = z + 1 ⇒ ∆ x = log a (z + 1) = ln (z + 1) ln a . Za posljednji prijelaz koristi se formula za prijelaz na novu bazu logaritma.

Izvršimo zamjenu u originalnom limitu:

(ax) " = ax lim ∆ x → 0 a ∆ x - 1 ∆ x = ax ln a lim ∆ x → 0 1 1 z ln (z + 1) = ax ln a lim ∆ x → 0 1 ln (z + 1) 1 z = ax ln a 1 ln lim ∆ x → 0 (z + 1) 1 z

Prisjetimo se druge izvanredne granice i tada ćemo dobiti formulu za izvod eksponencijalna funkcija:

(a x) " = a x ln a 1 ln lim z → 0 (z + 1) 1 z = a x ln a 1 ln e = a x ln a

Primjer 3

Date su eksponencijalne funkcije:

f 1 (x) = 2 3 x , f 2 (x) = 5 3 x , f 3 (x) = 1 (e) x

Moramo pronaći njihove derivate.

Rješenje

Koristimo formulu za izvod eksponencijalne funkcije i svojstva logaritma:

f 1 "(x) = 2 3 x" = 2 3 x ln 2 3 = 2 3 x (ln 2 - ln 3) f 2 "(x) = 5 3 x" = 5 3 x ln 5 1 3 = 1 3 5 3 x ln 5 f 3 "(x) = 1 (e) x" = 1 ex "= 1 ex ln 1 e = 1 ex ln e - 1 = - 1 ex

Derivat logaritamske funkcije

Dokaz 5

Predstavljamo dokaz formule za izvod logaritamske funkcije za bilo koje x u domeni definicije i bilo koje važeće vrijednosti osnove a logaritma. Na osnovu definicije derivacije dobijamo:

(log ax) " = lim ∆ x → 0 log a (x + ∆ x) - log ax ∆ x = lim ∆ x → 0 log ax + ∆ xx ∆ x = = lim ∆ x → 0 1 ∆ x log a 1 + ∆ xx = lim ∆ x → 0 log a 1 + ∆ xx 1 ∆ x = = lim ∆ x → 0 log a 1 + ∆ xx 1 ∆ x xx = lim ∆ x → 0 1 x log a 1 + ∆ xxx ∆ x = = 1 x log a lim ∆ x → 0 1 + ∆ xxx ∆ x = 1 x log ae = 1 x ln e ln a = 1 x ln a

Iz navedenog lanca jednakosti se vidi da su transformacije izgrađene na osnovu svojstva logaritma. Jednakost lim ∆ x → 0 1 + ∆ x x x ∆ x = e je tačna u skladu sa drugom značajnom granicom.

Primjer 4

Logaritamske funkcije su date:

f 1 (x) = log log 3 x , f 2 (x) = log x

Potrebno je izračunati njihove derivate.

Rješenje

Primijenimo izvedenu formulu:

f 1 "(x) = (log ln 3 x)" = 1 x ln (ln 3) ; f 2 "(x) = (ln x)" = 1 x ln e \u003d 1 x

Dakle, izvod prirodnog logaritma je jedan podijeljen sa x.

Derivati trigonometrijskih funkcija

Dokaz 6

Koristimo neke trigonometrijske formule i prva izvanredna granica za izvođenje formule za izvod trigonometrijske funkcije.

Prema definiciji derivacije sinusne funkcije, dobijamo:

(sin x) " = lim ∆ x → 0 sin (x + ∆ x) - sin x ∆ x

Formula za razliku sinusa omogućit će nam da izvršimo sljedeće radnje:

(sin x) " = lim ∆ x → 0 sin (x + ∆ x) - sin x ∆ x = = lim ∆ x → 0 2 sin x + ∆ x - x 2 cos x + ∆ x + x 2 ∆ x = = lim ∆ x → 0 sin ∆ x 2 cos x + ∆ x 2 ∆ x 2 = = cos x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2

Konačno, koristimo prvu divnu granicu:

sin "x = cos x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = cos x

Dakle, derivacija funkcije sin xće cos x.

Na isti način ćemo dokazati i formulu za kosinusni derivat:

cos "x = lim ∆ x → 0 cos (x + ∆ x) - cos x ∆ x = = lim ∆ x → 0 - 2 sin x + ∆ x - x 2 sin x + ∆ x + x 2 ∆ x = = - lim ∆ x → 0 sin ∆ x 2 sin x + ∆ x 2 ∆ x 2 = = - sin x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = - sin x

One. derivacija funkcije cos x će biti – sin x.

Izvodimo formule za izvode tangente i kotangensa na osnovu pravila diferencijacije:

tg "x = sin x cos x" = sin "x cos x - sin x cos" x cos 2 x = = cos x cos x - sin x (- sin x) cos 2 x = sin 2 x + cos 2 x cos 2 x = 1 cos 2 xctg "x = cos x sin x" = cos "x sin x - cos x sin" x sin 2 x = = - sin x sin x - cos x cos x sin 2 x = - sin 2 x + cos 2 x sin 2 x = - 1 sin 2 x

Derivati inverznih trigonometrijskih funkcija

Derivativna sekcija inverzne funkcije daje sveobuhvatne informacije o dokazu formula za izvode arksinusa, arkkosinusa, arktangensa i arkkotangensa, tako da ovdje nećemo duplirati materijal.

Derivati hiperboličkih funkcija

Dokaz 7

Možemo izvesti formule za izvode hiperboličkog sinusa, kosinusa, tangenta i kotangensa koristeći pravilo diferencijacije i formulu za izvod eksponencijalne funkcije:

sh "x = ex - e - x 2" = 1 2 ex " - e - x " == 1 2 ex - - e - x = ex + e - x 2 = chxch " x = ex + e - x 2 " = 1 2 ex "+e - x" == 1 2 ex + - e - x = ex - e - x 2 = shxth "x = shxchx" = sh "x chx - shx ch" xch 2 x = ch 2 x - sh 2 xch 2 x = 1 ch 2 xcth "x = chxshx" = ch "x shx - chx sh" xsh 2 x = sh 2 x - ch 2 xsh 2 x = - 1 sh 2 x

Ako primijetite grešku u tekstu, označite je i pritisnite Ctrl+Enter

Za pronalaženje derivacija trigonometrijske funkcije potrebno koristiti tabela derivata, odnosno derivati 6-13.

Kada se nađe derivati jednostavnih trigonometrijskih funkcija Da biste izbjegli uobičajene greške, obratite pažnju na sljedeće točke:

u izrazu funkcije, jedan od pojmova je često sinus, kosinus ili druga trigonometrijska funkcija ne iz argumenta funkcije, već iz broja (konstante), pa je izvod ovog člana jednak nuli;
gotovo uvijek trebate pojednostaviti izraz koji se dobije kao rezultat diferencijacije, a za to morate pouzdano koristiti znanje o operacijama s razlomcima;
da bi se izraz pojednostavio, gotovo uvijek treba znati trigonometrijske identitete, kao što su formula dvostrukog ugla i formula jedinice kao zbir kvadrata sinusa i kosinusa.

Primjer 1 Pronađite izvod funkcije

Rješenje. Recimo sa kosinus derivat sve je jasno, reći će mnogi koji počnu proučavati derivate. Kako bi bilo sa sinusni derivat dvanaest podeljeno sa pi? Odgovor: smatrajte jednakim nuli! Ovdje je sinus (funkcija ipak!) zamka, jer argument nije varijabla x ili bilo koja druga varijabla, već samo broj. Odnosno, sinus ovog broja je takođe broj. A derivacija broja (konstanta), kao što znamo iz tabele derivata, jednaka je nuli. Dakle, ostavljamo samo minus sinus od x i nalazimo njegovu derivaciju, ne zaboravljajući znak:

Primjer 2 Pronađite izvod funkcije

Rješenje. Drugi pojam je isti slučaj kao i prvi u prethodnom primjeru. To jest, broj, a derivacija broja je nula. Izvod drugog člana nalazimo kao izvod količnika:

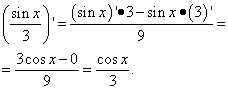
Primjer 3 Pronađite izvod funkcije

Rješenje. Ovo je drugačiji zadatak: ovdje u prvom članu ne postoji ni arksinus ni druga trigonometrijska funkcija, ali postoji x, što znači da je ovo funkcija od x. Stoga ga razlikujemo kao pojam u zbiru funkcija:

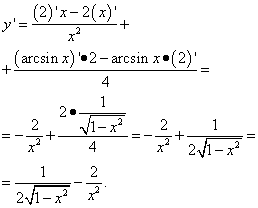
Ovdje su bile potrebne vještine u akcijama s razlomcima, odnosno u eliminaciji trokatnog razlomka.

Primjer 4 Pronađite izvod funkcije

Rješenje. Ovdje slovo "fi" igra istu ulogu kao "X" u prethodnim slučajevima (i u većini drugih, ali ne u svim) - nezavisna varijabla. Stoga, kada tražimo derivaciju proizvoda funkcija, nećemo žuriti da proglasimo derivaciju korijena "phi" jednakom nuli. dakle:

Ali rješenje se tu ne završava. Budući da su slični članovi skupljeni u dvije zagrade, još uvijek moramo transformirati (pojednostaviti) izraz. Stoga množimo zagrade sa faktorima uzetim iz njih, a zatim sve članove svodimo na zajednički nazivnik i izvodimo druge elementarne transformacije:

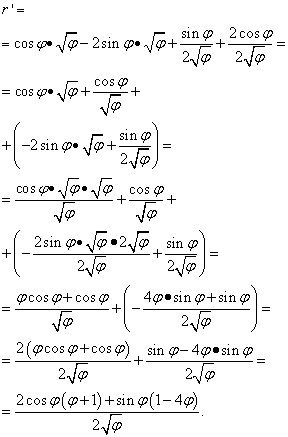
Primjer 5 Pronađite izvod funkcije

Rješenje. U ovom primjeru morat ćemo znati činjenicu da postoji takva trigonometrijska funkcija - sekansa - i njene formule u smislu kosinusa. razlikovati:

Primjer 6 Pronađite izvod funkcije

Rješenje. U ovom primjeru morat ćemo zapamtiti formulu dvostrukog ugla iz školskog kursa. Ali prvo, hajde da razlikujemo:

(ovo je formula dvostrukog ugla)

Diferencijalni račun funkcije jedne varijable

1. Uvod

Matematička analiza- grana matematike koja je nastala u 18. veku i obuhvata dva glavna dela: diferencijalni i integralni račun. Izvod funkcije je jedan od osnovnih matematičkih pojmova diferencijalni račun. Analiza je nastala zahvaljujući naporima mnogih matematičara (prije svega I. Newtona i G. Leibniza) i odigrala je ogromnu ulogu u razvoju prirodnih znanosti - moćne, prilično univerzalne metode za proučavanje funkcija koje nastaju pri rješavanju različitih primijenjenih problema se pojavio.

2. Numerička funkcija. Shema proučavanja funkcija.

(Pogledajte napomene o temi "Funkcija napajanja")

1) Opseg funkcije.

2) Skup vrijednosti funkcije.

3) Parne, neparne funkcije.

4) Monotonost funkcije.

5) Reverzibilnost funkcije.

6) Nule funkcije.

7) Intervali konstantnosti predznaka funkcije.

8) Ograničena funkcija.

Vježbe:

Pronađite opseg funkcije:

ali) ; b) ; u) .

ali) ; b) ; G) .

3. Koncept granice funkcije u tački.

Razmotrimo grafove nekih funkcija. Proučimo ponašanje funkcija u blizini tačke x 0 , odnosno u nekom susjedstvu tačke x 0 .

Rice. 1. Fig. 2. Fig. 3.

Funkcija ima svojstvo koje je razlikuje od druge dvije funkcije.

1. Prilikom pristupa argumentaciji X to x 0 s lijeve i desne strane odgovarajuće vrijednosti funkcije su proizvoljno bliske istom broju ALI.

Druge dvije funkcije nemaju ovo svojstvo.

2. Kada pristupite argumentu X to x 0 na lijevoj strani, odgovarajuće vrijednosti funkcije su proizvoljno bliske broju ALI, i kada se pristupi argumentu X to x 0 na desnoj strani, odgovarajuće vrijednosti funkcije su proizvoljno bliske broju IN.

3. Funkcija pri pristupu argumentu X to x 0 lijevo i desno poprimaju različite vrijednosti.

Izlaz: Ako pri pristupu argumentu X to x 0 na lijevoj i desnoj strani, točke s koordinatama su proizvoljno blizu točke s koordinatama , zatim .

Primjer: Obavlja funkciju granica u tačkama x 1, x 2, x 3, x 4, x 5?

Odgovor: Funkcija ima ograničenje u tačkama x 1 , x 3 ;

funkcija nema ograničenja u tačkama x 2 , x 4 , x 5 .

Komentar:

4. Definicija funkcije kontinuirane u tački i na intervalu

Koncept kontinuiteta funkcije prikladno je povezan s idejom grafa ove funkcije kao "neprekidne" (pune) linije. Puna linija je linija povučena bez podizanja olovke sa papira.

Pitanje: Koje od ovih funkcija su kontinuirane?

Rice. 1. Fig. 2. Fig. 3.

Rice. 4. Fig. pet.

Odgovor: Od ovih funkcija, funkcija prikazana na slici 1 je kontinuirana. br. 3, pošto je njen graf „neprekidna“ (puna) linija.

Pitanje: Koja su svojstva funkcije prikazane na Sl. br. 3, a nemate druge funkcije?

odgovor:

1. Funkcija je definirana u tački x 0. Ovo svojstvo ne vrijedi za funkciju prikazanu na sl. br. 1.

2. Postoji konačan limit funkcije u tački x 0. Ovo svojstvo ne vrijedi za funkcije prikazane na sl. br. 2, 5.

3. Granica funkcije u tački x 0 jednaka je vrijednosti funkcije u ovoj tački, tj. . Ovo svojstvo ne vrijedi za funkciju prikazanu na sl. br. 4.

Svojstva koja su zadovoljena za funkciju prikazanu na sl. br. 3, i omogućavaju definiranje funkcije kontinuirane u tački x 0 .

Definicija: Kaže se da je funkcija kontinuirana u jednoj tački x 0, ako .

Komentar: Ako je funkcija kontinuirana u nekoj tački x 0, onda pokažite x 0 naziva se tačka kontinuiteta funkcije ako funkcija nije kontinuirana u toj tački x 0, onda pokažite x 0 naziva se tačka prekida funkcije.

Definicija: Funkcija se naziva kontinuiranom na intervalu ako je kontinuirana u svakoj tački tog intervala.

5. Povećanje argumenta, povećanje funkcije

Neka funkcija , biti zadana.

x 0 - početna vrijednost argumenta, ;

X- konačna vrijednost argumenta, ;

f (x 0) - početna vrijednost funkcije;

f(x 0 + D x) - konačnu vrijednost funkcije.

Definicija: Razlika između krajnje i početne vrijednosti argumenta naziva se povećanjem argumenta. D x \u003d x - x 0

Definicija: Razlika između konačne i početne vrijednosti funkcije naziva se inkrement funkcije. D y \u003d f (x 0 + D x) - f (x 0)

Komentar:

Geometrijski povećavajući argument D x– je razlika između apscisa tačaka grafa funkcije koje odgovaraju konačnoj i početnoj vrijednosti argumenta.
Funkcija geometrijskog povećanja D y– je razlika između ordinata točaka grafa funkcije koje odgovaraju konačnoj i početnoj vrijednosti argumenta.
Povećanje argumenta i povećanje funkcije mogu biti pozitivni ili negativni.

6. Koncept derivacije funkcije. fizičko značenje derivirajuća funkcija

Razmotrimo problem brzine promjene funkcije , gdje je X I at može biti bilo koja fizička veličina.

x 0 - početna vrijednost argumenta; f (x 0) - početna vrijednost funkcije;

x 0 +D x - konačna vrijednost argumenta; f(x 0 + D x) - konačna vrijednost funkcije;

D y \u003d f (x 0 + D x) - f (x 0) - prirast funkcije;

– prosječna stopa promjene funkcije u intervalu D x .

– trenutna brzina promjene funkcije, brzina promjene funkcije u tački x 0.

Definicija: Derivat funkcije u tački x 0 naziva se granica omjera prirasta D funkcioniše u jednom trenutku x 0 povećati D x argument kada inkrement argumenta teži nuli.

Izlaz: Derivat funkcije u tački x 0 je stopa promjene funkcije u tački x 0.

Teorema: Derivat konstantne funkcije y = c u bilo kom trenutku jednako nuli.

Teorema: Derivat funkcije y = x u bilo kom trenutku jednako jedan .

Komentar: Pronalaženje derivacije date funkcije naziva se diferencijacija.

7. Pravila za razlikovanje zbira, proizvoda, količnika funkcija

Razmotrite funkciju , koji se sastoji od dvije druge funkcije i , ima derivacije na intervalu :

3) .

Teorema #1: Derivat zbira (razlike) dvije funkcije jednak je zbroju (razlici) izvoda ovih funkcija.

Primjer: Izračunajte derivaciju funkcije

Teorema #2: Derivat proizvoda dvije funkcije određuje se formulom:

Posljedica: Konstantni faktor se može izvaditi iz predznaka derivacije: .

dokaz: .

Primjer

Vježbe:

2) ;

Derivat funkcije snage at izračunava se po formuli:

Komentar: Formula je važeća za funkciju stepena s bilo kojim eksponentom. ,

Primjer: Izračunajte derivate funkcija:

Izlaz: .

Vježbe: Izračunajte derivate funkcija:

; 2) ; 3) ;

4) ; 5) ;

6) ; 7) .

Teorema #3: Derivat kvocijenta dvije funkcije određuje se formulom:

Posljedice: ;

Primjer: Izračunajte derivate funkcija:

2) . .

3) . .

Vježbe: Izračunajte derivate funkcija:

1. ; 2. ; 3. ;

4. ; 5. ; 6.

;

; 8. ; 9.

8. Koncept kompleksne funkcije

Pravilo diferencijacije složenih funkcija

Neka je funkcija definirana na skupu , a funkcija na skupu , a za , odgovarajuća vrijednost . Tada se definira funkcija na skupu, koja se poziva složena funkcija iz X (funkcija od funkcije).

Varijabla se naziva srednji argument kompleksne funkcije.

Primjer:

Vježbe:

Iz koje elementarne funkcije Ove složene funkcije se sastoje od:

1) ; 2) ;

; 4) .

Sastavite složene funkcije od ovih elementarnih funkcija:

1) , ; 2) , ;

3) , . 4) , , .

Izlaz: Derivat kompleksne funkcije jednak je proizvodu izvoda elementarnih funkcija koje je čine .

Primjer: Izračunajte derivate funkcija:

- snaga, linearna; , .

- snaga, kvadratna; , .

Vježbe: Izračunajte derivate funkcija:

1. ; 2.

;

3. ; 4. ;

; 6. .

9. Derivat eksponencijalnih, logaritamskih funkcija

Primjer: Izračunajte derivate funkcija:

1. . .

2. . .

3. . .

Primjer: Izračunajte derivate funkcija:

1. . .

2. . .

Vježbe: Izračunajte derivaciju funkcije:

1. ; 2. ; 3. ;

4. ; 5. ; 6. ;

7. ; 8. .

10. Derivati trigonometrijskih funkcija

Derivati inverznih trigonometrijskih funkcija

Primjer: Izračunajte derivate funkcija:

1. . .

2. . .

Zadatak

. .

Zadatak: Izračunajte derivaciju funkcije.

Vježba: Izračunajte derivaciju funkcije.

Derivati inverznih trigonometrijskih funkcija

;

Vježbe: Izračunajte derivate funkcija:

1. 2.

3. 4.

5. 6. 7. 8. 9.

10.

11. 12. 13.

11. geometrijskog smisla derivirajuća funkcija

Razmotrimo funkciju.

Uzmite fiksnu tačku na grafu funkcije i proizvoljna tačka . Nacrtajmo sekantu . Ako je poenta M kretati se u nedogled do tačke M 0 prema grafu funkcije , zatim sekansa M 0 M će zauzeti različite pozicije i ako se tačka poklopi M sa tačkom M 0 sekanti će zauzeti graničnu poziciju M 0 T , zatim prava linija M 0 T će biti tangenta na graf funkcije u tački M 0 .

Definicija: Tangenta na graf funkcije u tački M 0 zove granica M 0 T secant dok stremi bodu M prema rasporedu do tačke M 0 .

b- ugao nagiba sekante M 0 M

a- ugao nagiba tangente M 0 T u pozitivnom smjeru x-ose.

Nagib sekansa M 0 M .

Tangent Slope M 0 T .

Razmotrimo pravougli trougao M 0 MA (). Tangenta oštrog ugla pravougaonog trougla jednak omjeru suprotne noge i susjedne:

tj . A to znači .

Definirajte derivaciju funkcije u tački x 0 : .

, , Shodno tome, .

Izlaz: Geometrijsko značenje izvoda funkcije je da je derivacija funkcije u jednaka nagibu tangente povučene na graf funkcije u tački sa apscisom.

Primjer:

1. Pronađite nagib tangente povučene na graf funkcije u tačkama .

; ; ; ; ; .

Odgovor: ; ; .

2. Odrediti ugao nagiba tangente povučene na graf funkcije u tački sa apscisom.

; ; ; ; . paralelno sa pravom linijom;

Hajde da instaliramo neophodno stanje postojanje ekstremuma.

Fermatova teorema: Ako je unutrašnja točka x 0 van delokruga kontinuirana funkcija je tačka ekstrema i u ovoj tački postoji derivacija, tada je jednaka nuli.

Komentar: Međutim, jednakost nule derivacije funkcije u tački x 0 i dalje ne daje za pravo da to tvrdi x 0 – tačka ekstrema funkcije.

Prilikom izvođenja prve formule tablice, polazit ćemo od definicije derivacije funkcije u tački. Hajde da uzmemo gde x- bilo koji realan broj, tj. x– bilo koji broj iz područja definicije funkcije. Zapišimo granicu omjera prirasta funkcije i prirasta argumenta na:

Treba napomenuti da se pod znakom granice dobija izraz, koji nije nesigurnost nule podijeljene sa nulom, jer brojnik ne sadrži beskonačno malu vrijednost, već upravo nulu. Drugim riječima, prirast konstantne funkcije je uvijek nula.

Na ovaj način, derivacija konstantne funkcijejednaka je nuli na cijelom domenu definicije.

Derivat funkcije stepena.

Formula za izvod funkcije stepena ima oblik , gdje je eksponent str je bilo koji realan broj.

Hajde da prvo dokažemo formulu za prirodni eksponent, odnosno za p = 1, 2, 3, ...

Koristićemo definiciju derivata. Zapišimo granicu omjera prirasta funkcije snage i prirasta argumenta:

Da bismo pojednostavili izraz u brojiocu, okrećemo se Newtonovoj binomnoj formuli:

shodno tome,

Ovo dokazuje formulu za izvod funkcije stepena za prirodni eksponent.

Derivat eksponencijalne funkcije.

Izvodimo formulu derivata na osnovu definicije:

Došao u neizvjesnost. Da bismo ga proširili, uvodimo novu varijablu , i za . Onda . U posljednjem prijelazu koristili smo formulu za prijelaz na novu bazu logaritma.

Izvršimo zamjenu u originalnom limitu:

Ako se prisjetimo druge izvanredne granice, dolazimo do formule za izvod eksponencijalne funkcije:

Derivat logaritamske funkcije.

Dokažimo formulu za izvod logaritamske funkcije za sve x iz opsega i svih važećih osnovnih vrijednosti a logaritam. Po definiciji derivacije, imamo:

Kao što ste primijetili, u dokazu su transformacije provedene korištenjem svojstava logaritma. Jednakost vrijedi zbog drugog značajnog ograničenja.

Derivati trigonometrijskih funkcija.

Da bismo izveli formule za izvode trigonometrijskih funkcija, morat ćemo se prisjetiti nekih trigonometrijskih formula, kao i prve izvanredne granice.

Po definiciji derivacije za sinusnu funkciju, imamo .

Koristimo formulu za razliku sinusa:

Ostaje da se okrenemo prvoj izuzetnoj granici:

Dakle, derivacija funkcije sin x jesti cos x.

Formula za kosinusni derivat je dokazana na potpuno isti način.

Dakle, derivacija funkcije cos x jesti –sin x.

Izvođenje formula za tablicu izvoda za tangentu i kotangens vršit će se korištenjem dokazanih pravila diferencijacije (derivacija razlomka).

Derivati hiperboličkih funkcija.

Pravila diferencijacije i formula za izvod eksponencijalne funkcije iz tablice derivacija nam omogućavaju da izvedemo formule za izvode hiperboličkog sinusa, kosinusa, tangenta i kotangensa.

Derivat inverzne funkcije.

Kako ne bi bilo zabune u prezentaciji, označimo u donjem indeksu argument funkcije pomoću koje se vrši diferencijacija, odnosno derivacija funkcije f(x) on x.

Sada formulišemo pravilo za pronalaženje derivacije inverzne funkcije.

Neka funkcije y = f(x) I x = g(y) međusobno inverzne, definisane na intervalima i respektivno. Ako u nekoj tački postoji konačan izvod funkcije koji nije nula f(x), tada u točki postoji konačan izvod inverzne funkcije g(y), i . U drugom unosu .

Ovo pravilo se može preformulisati za bilo koje x iz intervala , onda dobijamo .

Provjerimo valjanost ovih formula.

Nađimo inverznu funkciju za prirodni logaritam (ovdje y je funkcija, i x- argument). Rješavanje ove jednadžbe za x, dobijamo (ovde x je funkcija, i y njen argument). tj. i međusobno inverzne funkcije.

Iz tabele derivata to vidimo I .

Uvjerimo se da nas formule za pronalaženje izvoda inverzne funkcije dovode do istih rezultata:

Kao što vidite, dobili smo iste rezultate kao u tabeli derivata.

Sada imamo znanje da dokažemo formule za izvode inverznih trigonometrijskih funkcija.

Počnimo s derivacijom arcsinusa.

. Tada, po formuli za izvod inverzne funkcije, dobijamo

Ostaje da se izvrši transformacija.

Pošto je raspon arksinusa interval , onda (pogledajte odjeljak o osnovnim elementarnim funkcijama, njihovim svojstvima i grafovima). Stoga, ne razmatramo.