Granica beskonačno male vrijednosti. Primjeri

Iz Wikipedije, slobodne enciklopedije

Infinitezimal - numerička funkcija ili niz koji teži nuli.

beskonačno velika- numerička funkcija ili niz koji teži beskonačnosti određenog znaka.

Račun beskonačno malih i velikih

Infinitezimalni račun- proračuni izvedeni sa beskonačno malim vrijednostima, u kojima se izvedeni rezultat smatra beskonačnim zbirom infinitezimalnih. Infinitezimalni račun je opšti koncept za diferencijalni i integralni račun, koji čine osnovu moderne više matematike. Koncept beskonačno male količine usko je povezan sa konceptom granice.

Infinitezimal

Subsequence $a_n$ pozvao beskonačno mali, ako $\lim\limits_(n\to\infty)a_n=0$ . Na primjer, niz brojeva $a_n=\dfrac(1)(n)$ - beskonačno mali.

Funkcija se poziva beskonačno mali u okolini tačke $x_0$ , ako $\lim\limits_(x\to x_0)f(x)=0$ .

Funkcija se poziva beskonačno mali u beskonačnosti, ako $\lim\limits_(x\to+\infty)f(x)=0$ ili $\lim\limits_(x\to-\infty)f(x)=0$ .

Također beskonačno mala je funkcija koja je razlika između funkcije i njene granice, odnosno ako $\lim\limits_(x\to+\infty)f(x)=a$ , onda $f(x)-a=\alpha(x)$ , $\lim\limits_(x\to+\infty)(f(x)-a)=0$ .

Naglašavamo da infinitezimalnu vrijednost treba shvatiti kao varijabilnu vrijednost (funkciju), koja je samo u procesu promene[kada nastoji $x$ to $a$ (od $\lim\limits_(x\to a)f(x)=0$ )] je napravljen manjim od proizvoljnog broja ( $\varepsilon$ ). Stoga je, na primjer, izjava poput "miliontog dijela beskonačno mala vrijednost" netačna: nema smisla reći za broj [apsolutnu vrijednost] da je beskonačno mali.

beskonačno velika

U svim formulama ispod, beskonačnost desno od jednakosti implicira određeni znak (bilo "plus" ili "minus"). To je, na primjer, funkcija $x\sin x$ , neograničeno s obje strane, nije beskonačno veliko za $x\to+\infty$ .

Subsequence $a_n$ pozvao beskonačno velika, ako $\lim\limits_(n\to\infty)a_n=\infty$ .

Funkcija se poziva beskonačno velika u blizini tačke $x_0$ , ako $\lim\limits_(x\to x_0)f(x)=\infty$ .

Funkcija se poziva beskonačno veliko u beskonačnosti, ako $\lim\limits_(x\to+\infty)f(x)=\infty$ ili $\lim\limits_(x\to-\infty)f(x)=\infty$ .

Kao iu slučaju beskonačno malih, treba napomenuti da se nijedna pojedinačna vrijednost beskonačno velike količine ne može nazvati "beskonačno velikom" - beskonačno velika količina je funkcija koja samo u procesu promene može biti veći od proizvoljnog broja.

Svojstva infinitezimala

Algebarski zbir konačnog broja beskonačno malih funkcija je beskonačan mala funkcija.
Umnožak infinitezimala je beskonačno mali.
Proizvod beskonačno malog niza sa ograničenim je beskonačno mali. Kao posljedica toga, proizvod infinitezimalnog na konstantu je beskonačno mali.
Ako $a_n$ je beskonačno mali niz koji čuva znak $b_n=\dfrac(1)(a_n)$ je beskonačno veliki niz.

Poređenje infinitezimala

Definicije

Pretpostavimo da imamo beskonačno male za isto $x\to a$ količine $\alpha(x)$ I $\beta(x)$ (ili, što nije važno za definiciju, infinitezimalni nizovi).

Ako $\lim\limits_(x\to a)\dfrac(\beta)(\alpha)=0$ , onda $\beta$ - beskonačno mali viši red malenosti, kako $\alpha$ . odrediti $\beta=o(\alpha)$ ili $\beta\prec\alpha$ .
Ako $\lim\limits_(x\to a)\dfrac(\beta)(\alpha)=\infty$ , onda $\beta$ - beskonačno mali najniži red malenosti, kako $\alpha$ . Odnosno $\alpha=o(\beta)$ ili $\alpha\prec\beta$ .
Ako $\lim\limits_(x\to a)\dfrac(\beta)(\alpha)=c$ (granica je konačna i nije jednaka 0), tada $\alpha$ I $\beta$ su beskonačno male količine jednog reda veličine. Ovo je označeno kao $\alpha\asymp\beta$ ili kao istovremeno izvršavanje odnosa $\beta=O(\alpha)$ I $\alpha=O(\beta)$ . Treba napomenuti da se u nekim izvorima može naići na oznaku kada je istovetnost naredbi zapisana u obliku samo jednog “velikog o” omjera, što je slobodna upotreba ovog simbola.
Ako $\lim\limits_(x\to a)\dfrac(\beta)(\alpha^m)=c$ (granica je konačna i nije jednaka 0), zatim beskonačno mala količina $\beta$ Ima $m$ -ti red malenosti relativno beskonačno mali $\alpha$ .

Za izračunavanje takvih granica zgodno je koristiti L'Hospitalovo pravilo.

Primeri poređenja

At $(x\do 0)$ magnitude $x^5$ Ima višeg reda malenkost u odnosu na $x^3$ , jer $\lim\limits_(x\to 0)\dfrac(x^5)(x^3)=0$ . S druge strane, $x^3$ ima najniži red malenosti u odnosu na $x^5$ , jer $\lim\limits_(x\to 0)\dfrac(x^3)(x^5)=\infty$ .

Koristeći O-simboli dobijenih rezultata mogu se napisati u sljedećem obliku

x^5=o(x^3)

$\lim\limits_(x\to 0)\dfrac(2x^2+6x)(x)=\lim\limits_(x\to 0)\dfrac(2x+6)(1)=\lim\limits_(x \do 0)(2x+6)=6,$ odnosno kada $x\do 0$ funkcije $f(x)=2x^2+6x$ I $g(x)=x$ su beskonačno male količine istog reda.

U ovom slučaju, unosi

2x^2+6x = O(x)

x = O(2x^2+6x).

At $(x\do 0)$ beskonačno mali $2x^3$ ima treći red malenosti u odnosu na $x$ , ukoliko $\lim\limits_(x\to 0)\dfrac(2x^3)(x^3)=2$ , beskonačno mali $0(,)7x^2$ - drugi red, beskonačno mali $\sqrt(x)$ - red 0,5.

Ekvivalentne količine

Definicija

Ako $\lim\limits_(x\to a)\dfrac(\beta)(\alpha)=1$ , zatim beskonačno male ili beskonačno velike količine $\alpha$ I $\beta$ pozvao ekvivalentan(označeno kao $\alpha\thicksim\beta$ ).

Očigledno, ekvivalentne količine su poseban slučaj beskonačno malih (beskonačno velikih) količina istog reda male veličine.

At vrijede sljedeće relacije ekvivalencije (kao posljedica takozvanih izuzetnih granica):

$\sin\alpha(x)\thicksim\alpha(x);$
$\mathrm(tg)\,\alpha(x)\thicksim\alpha(x);$
$\arcsin(\alpha(x))\thicksim\alpha(x);$
$\mathrm(arctg)\,\alpha(x)\thicksim\alpha(x);$
$\log_a(1+\alpha(x))\thicksim\alpha(x)\cdot\frac(1)(\ln(a))$ , gdje $a>0$ ;
$\ln(1+\alpha(x))\thicksim\alpha(x);$
$a^(\alpha(x))-1\thicksim\alpha(x)\cdot\ln(a)$ , gdje $a>0$ ;
$e^(\alpha(x))-1\thicksim\alpha(x);$
$1-\cos(\alpha(x))\thicksim\frac(\alpha^2(x))(2);$
$(1+\alpha(x))^\mu-1\thicksim\mu\cdot\alpha(x),\quad\mu\in\R$ , pa koristite izraz:

\sqrt[n](1+\alpha(x))\približno\frac(\alpha(x))(n)+1

, gdje

\alpha(x)\xrightarrow()0

Teorema

Granica količnika (omjera) dvije beskonačno male ili beskonačno velike količine neće se promijeniti ako se jedna od njih (ili obje) zamijeni ekvivalentnom vrijednošću.

Ova teorema je od praktične važnosti za pronalaženje granica (vidi primjer).

Primjeri korištenja

Naći $\lim\limits_(x\to 0)\dfrac(\sin 2x)(x).$

Zamjena

\sin 2x

ekvivalentna vrijednost

2x

, dobijamo

\lim\limits_(x\to 0)\dfrac(\sin 2x)(x)=\lim\limits_(x\to 0)\dfrac(2x)(x)=2.

Naći $\lim\limits_(x\to\frac(\pi)(2))\dfrac(\sin(4\cos x))(\cos x).$

Jer

\sin(4\cos x)\thicksim(4\cos x)

x\to\dfrac(\pi)(2)

dobijamo

\lim\limits_(x\to \frac(\pi)(2))\dfrac(\sin(4\cos x))(\cos x)=\lim\limits_(x\to\frac(\pi) (2))\dfrac(4\cos x)(\cos x)=4.

Izračunati $\sqrt(1(,)2)$ .

Koristeći formulu:

\sqrt(1(,)2)\približno 1+\frac(0(,)2)(2)=1(,)1

, koristeći kalkulator (tačnije proračune), dobili smo:

\sqrt(1(,)2)\približno 1(,)095

, pa je greška bila 0,005 (manje od 1%), odnosno metoda je korisna, zbog svoje jednostavnosti, sa grubom procjenom aritmetičkih korijena blizu jedan.

istorija

Matematičari stare škole su podvrgli koncept beskonačno mali oštre kritike. Michel Rolle je napisao da je nova računica " skup briljantnih grešaka»; Voltaire je otrovno istakao da je ovaj račun umjetnost izračunavanja i preciznog mjerenja stvari čije postojanje nije moguće dokazati. Čak je i Hajgens priznao da ne razume značenje diferencijala višeg reda.

Kao ironiju sudbine može se smatrati pojava nestandardne analize sredinom 20. veka, koja je dokazala da je prvobitno gledište – stvarne infinitezimale – takođe konzistentno i da može biti osnova analize. Pojavom nestandardne analize postalo je jasno zašto su matematičari 18. veka, izvođenje nezakonitih sa stanovišta klasična teorija akcije su ipak dale prave rezultate.

vidi takođe

Napišite recenziju na članak "Beskonačno malo i beskonačno veliko"

Bilješke

Književnost

// Enciklopedijski rječnik Brockhausa i Efrona: u 86 svezaka (82 sveska i 4 dodatna). - St. Petersburg. , 1890-1907.

Izvod koji karakterizira beskonačno malo i beskonačno veliko

„Pa, prijatelju, bojim se da ti i monah trošite svoj barut“, rekao je princ Andrej podrugljivo, ali umiljato.
- Ah! mon ami. [ALI! Moj prijatelj.] Samo se molim Bogu i nadam se da me On čuje. Andre,” rekla je stidljivo nakon trenutka ćutanja, “imam veliku molbu za tebe.
- Šta, prijatelju?
Ne, obećaj mi da nećeš odbiti. Neće vas koštati nikakvog posla i neće biti ničeg nedostojnog vas. Samo me ti možeš utješiti. Obećaj, Andryusha, - rekla je, stavljajući ruku u torbicu i držeći nešto u njoj, ali još ne pokazujući, kao da je ono što je držala predmet zahtjeva i kao da je prije nego što je primila obećanje da će ispuniti zahtjev ne mogu ga izvaditi iz torbice. To je nešto.
Ona je bojažljivo, molećivo pogledala brata.
„Kad bi me to koštalo mnogo posla...“ odgovorio je princ Andrej, kao da je nagađao šta je u pitanju.
- Šta god hoćeš, misli! Znam da si isti kao mon pere. Misli šta god hoćeš, ali uradi to za mene. Uradi to molim te! Otac mog oca, naš djed, nosio ga je u svim ratovima... - Još uvijek nije iz torbice izvukla ono što je držala. "Dakle, obećavaš mi?"
"Naravno, šta je bilo?"
- Andre, blagosloviću te imidžom, a ti mi obećaj da je nikada nećeš skinuti. Obećavam?
„Ako ne spusti vrat na dva kilograma... Da ti ugodi...“ rekao je princ Andrej, ali se istog trenutka, primetivši uznemireni izraz koji je lice njegove sestre poprimilo na ovu šalu, pokajao. „Veoma mi je drago, zaista mi je drago, prijatelju“, dodao je.
"Protiv vaše volje, On će vas spasiti i smilovati i okrenuti vas sebi, jer samo u Njemu je istina i mir", rekla je glasom drhtavim od uzbuđenja, svečanim pokretom držeći u obje ruke ispred sebe brat ovalna drevna ikona Spasitelja sa crnim licem u srebrnoj misnici na srebrnom lančiću fine izrade.
Prekrstila se, poljubila ikonu i pružila je Andreju.
– Molim te, Andre, za mene…
Iz njenih velikih očiju sijali su snopovi ljubazne i plašljive svjetlosti. Ove oči su obasjale celo bolesno, mršavo lice i učinile ga lepim. Brat je htio uzeti škapular, ali ga je zaustavila. Andrej je shvatio, prekrstio se i poljubio ikonu. Lice mu je bilo u isto vrijeme nježno (bio je dirnut) i podrugljivo.
- Merci, mon ami. [Hvala ti prijatelju.]
Poljubila ga je u čelo i ponovo sela na sofu. Ćutali su.
- Rekao sam ti, Andre, budi ljubazan i velikodušan, kao što si oduvek bio. Ne sudite Lise strogo, počela je. - Ona je tako slatka, tako ljubazna, a njen položaj je sada veoma težak.
- Izgleda da ti nisam ništa rekao, Maša, pa da svoju ženu zamerim ili da budem nezadovoljan njome. Zašto mi sve ovo govoriš?
Princeza Meri je pocrvenela na mrlje i zaćutala, kao da se oseća krivom.
„Nisam ti ništa rekao, ali ti je već rečeno. I rastužuje me.
Crvene mrlje su se još jače pojavile na čelu, vratu i obrazima princeze Marije. Htjela je nešto reći i nije mogla to izgovoriti. Brat je dobro pogodio: mala princeza je plakala posle večere, govorila da je predosećala nesretan porod, da ih se plašila i žalila se na svoju sudbinu, na svekra i muža. Nakon što je zaplakala, zaspala je. Princu Andreju je bilo žao svoje sestre.
- Znaj jedno, Maša, ne mogu da zamerim, nisam zamerio i nikada neću zameriti svojoj ženi, a ni sam sebi ne mogu ništa da zamerim u vezi sa njom; i uvek će biti tako, u kakvim god okolnostima bio. Ali ako želiš da znaš istinu... želiš da znaš da li sam srećan? br. Da li je sretna? br. Zašto je ovo? Ne znam…
Rekavši to, ustao je, prišao sestri i, sagnuvši se, poljubio je u čelo. Njegove prelijepe oči sijale su inteligentnim i ljubaznim, nenaviknutim sjajem, ali on nije gledao u svoju sestru, već u mrak otvorenih vrata, kroz njenu glavu.
- Idemo do nje, moramo se pozdraviti. Ili idi sama, probudi je, a ja ću odmah doći. Peršun! viknuo je sobaru, "dođi ovamo, očisti to." Na sjedištu je, na desnoj strani.
Princeza Marija je ustala i otišla do vrata. Ona je stala.
Andre, si vous avez. la foi, vous vous seriez adresse a Dieu, pour qu "il vous donne l" amour, que vous ne sentez pas et votre priere aurait ete exaucee. [Kada biste imali vjeru, obratili biste se Bogu s molitvom, da vam On da ljubav koju ne osjećate, a vaša molitva bi bila uslišena.]
- Da, zar ne! - rekao je princ Andrija. - Idi, Maša, dolazim odmah.
Na putu do sestrine sobe, u galeriji koja je spajala jednu kuću s drugom, princ Andrej je sreo slatko nasmejanu m lle Bourienne, po treći put tog dana sa oduševljenim i naivnim osmehom na koji je naišao u zabačenim prolazima.
- Ah! je vous croyais chez vous, [Ah, mislila sam da si u svojoj sobi,] rekla je, pocrvenevši iz nekog razloga i spustivši oči.
Princ Andrej ju je strogo pogledao. Na licu princa Andreja iznenada se pojavio bes. Ništa joj nije rekao, već joj je pogledao u čelo i kosu, ne gledajući je u oči, tako prezrivo da je Francuskinja pocrvenela i otišla ne rekavši ništa.
Kada je prišao sestrinoj sobi, princeza je već bila budna, a sa otvorenih vrata čuo se njen vedar glas, koji je žurio jednu reč za drugom. Govorila je kao da nakon dužeg perioda apstinencije želi da nadoknadi propušteno.
- Non, mais figurez vous, la vieille comtesse Zouboff avec de fausses boucles et la bouche pleine de fausses dents, comme si elle voulait defier les annees... [Ne, zamislite, stara grofica Zubova, s lažnim uvojcima, s lažnim zubima, kao da se rugam godinama...] Xa, xa, xa, Marieie!
Potpuno istu frazu o grofici Zubovoj i isti smeh već je pet puta pred strancima čuo princ Andrej od svoje žene.
Tiho je ušao u sobu. Princeza, punašna, rumenkasta, s poslom u rukama, sjedila je na fotelji i neprestano pričala, prebirajući peterburška sjećanja, pa čak i fraze. Prišao je princ Andrej, pomilovao je po glavi i upitao je li se odmorila od putovanja. Ona se javila i nastavila isti razgovor.
Kolica su stajala u šest na ulazu. Napolju je bila mračna jesenja noć. Kočijaš nije vidio vuču kočije. Ljudi sa lampionima vrpoljili su se na trijemu. Ogromna kuća je gorjela od svjetla kroz velike prozore. U predsoblju su se zbijali dvorovi, koji su htjeli da se oproste od mladog princa; u predsoblju su stajali svi ukućani: Mihail Ivanovič, m lle Bourienne, princeza Marija i princeza.
Princ Andrej je pozvan u kancelariju svog oca, koji je želeo da se oprosti s njim licem u lice. Svi su čekali da izađu.
Kada je princ Andrej ušao u kancelariju, stari princ, sa starčevim naočarima i u svom belom mantilu, u koji nije primio nikoga osim sina, sedeo je za stolom i pisao. Osvrnuo se.
- Ides li? I ponovo je počeo da piše.
- Došao sam da se pozdravim.
- Poljubi ovde, - pokazao je obraz, - hvala, hvala!
- Na čemu mi se zahvaljujem?
- Zato što ne prestaješ, ne držiš se za žensku suknju. Prvo servis. Hvala ti hvala ti! I nastavio je da piše, tako da je sprej poleteo sa pucketavog pera. - Ako treba nešto da kažeš, reci. Ove dvije stvari mogu raditi zajedno”, dodao je.
“U vezi sa svojom ženom… Tako me je sramota što je ostavljam u tvom naručju…”
- Šta lažeš? Reci šta ti treba.
- Kad vaša žena bude imala vremena da se porodi, pošaljite u Moskvu po akušera... Pa da bude tu.
Stari princ zastade i, kao da ne razume, zagleda se strogim očima u sina.
„Znam da niko ne može pomoći ako priroda ne pomogne“, rekao je princ Andrej, očigledno posramljen. „Slažem se da je od milion slučajeva jedan nesretan, ali ovo je njena i moja fantazija. Rekli su joj, vidjela je to u snu i plaši se.
“Hm... hm...” reče stari princ u sebi, nastavljajući da završava pisanje. - Hoću.
Precrtao je potpis, odjednom se brzo okrenuo sinu i nasmijao se.
- Loše je, zar ne?
- Šta nije u redu, oče?
- Žena! reče stari knez kratko i značajno.
„Ne razumem“, reče princ Andrej.
"Da, nema šta da se radi, prijatelju", rekao je princ, "svi su takvi, nećeš se oženiti." Ne boj se; neću nikome reći; i sami znate.
Zgrabio mu je ruku svojom koščatom rukom, protresao je, pogledao pravo u lice svog sina svojim brzim očima, koje kao da su prozirale čovjeka, i opet se nasmijao svojim hladnim smijehom.
Sin je uzdahnuo, priznavši ovim uzdahom da ga je otac razumio. Starac je, nastavivši da savija i štampa slova, uobičajenom brzinom, zgrabio je i bacio pečat, pečat i papir.
- Šta da radim? Beautiful! Uradiću sve. Smiri se”, rekao je kratko dok je kucao.
Andrej je ćutao: bilo mu je i prijatno i neprijatno što ga je otac razumeo. Starac je ustao i dao pismo svom sinu.
„Slušaj“, rekao je, „ne brini za svoju ženu: šta se može učiniti, biće učinjeno.“ Sada slušajte: dajte pismo Mihailu Ilarionoviču. Pišem da će te iskoristiti na dobrim mjestima i neće te dugo zadržati kao ađutanta: loša pozicija! Reci mu da ga se sjećam i da ga volim. Da, napiši kako će te prihvatiti. Ako je dobro, poslužite. Sin Nikolaja Andreja Bolkonskog, iz milosti, neće služiti nikome. Pa, sad dođi ovamo.
Govorio je tako brzo da nije završio ni pola riječi, ali sin je navikao da ga razumije. Odveo je sina do biroa, odbacio poklopac, izvukao fioku i izvadio svesku prekrivenu njegovim krupnim, dugačkim, sažetim rukopisom.
“Moram umrijeti prije tebe.” Znajte da su ovdje moje bilješke, da ih prenesem na vladara nakon moje smrti. Evo sad - evo založnice i pisma: ovo je nagrada onome ko piše istoriju Suvorovljevih ratova. Prijavite se na akademiju. Evo mojih napomena, nakon što pročitate sami, naći ćete nešto korisno.
Andrej nije rekao ocu da će vjerovatno još dugo živjeti. Znao je da ne treba to da kaže.
„Učiniću sve, oče“, rekao je.
- Pa, sad zbogom! Pustio je sina da mu poljubi ruku i zagrlio ga. "Zapamti jednu stvar, kneže Andreje: ako te ubiju, starac će me povrijediti..." Iznenada je zašutio i odjednom nastavio u sav glas: "a ako saznam da se nisi ponašao kao sin Nikolaj Bolkonski, biće me ... sramota! vrisnuo je.
„Nisi mi to mogao reći, oče“, rekao je sin, smiješeći se.
Starac je ćutao.
„Takođe sam hteo da te pitam“, nastavi princ Andrej, „ako me ubiju i ako budem imao sina, ne daj mu da ode od tebe, kao što sam ti rekao juče, da odraste sa tobom... molim te.
- Nemoj to dati svojoj ženi? rekao je starac i nasmijao se.
Stajali su ćutke jedno naspram drugog. Starčeve brze oči bile su uprte direktno u oči njegovog sina. Nešto je zadrhtalo u donjem dijelu lica starog princa.
- Zbogom... idi! iznenada je rekao. - Ustani! viknuo je ljutitim i glasnim glasom, otvarajući vrata radne sobe.
– Šta je, šta? - pitale su princeza i princeza, ugledavši princa Andreja i na trenutak lik starca u belom mantilu, bez perike i u staračkim naočarima, kako se naginje i vrišteći ljutitim glasom.
Princ Andrej je uzdahnuo i nije odgovorio.
„Pa“, rekao je, okrećući se ženi.
I ovo „dobro“ je zvučalo kao hladna sprdnja, kao da je govorio: „Sada se izvlačite“.
Andre, deja! [Andrej, već!] - reče mala princeza, prebledeći i sa strahom gledajući muža.
Zagrlio ju je. Vrisnula je i onesviještena pala na njegovo rame.
Nežno je povukao rame na kojem je ležala, pogledao joj u lice i pažljivo je posadio u stolicu.
- Adieu, Marieie, [Zbogom, Maša,] - rekao je tiho svojoj sestri, poljubio joj ruku u ruku i brzo izašao iz sobe.
Princeza je ležala u fotelji, m lle Bourienne je trljala sljepoočnice. Princeza Marija, podržavajući svoju snahu, suznih prelepih očiju, i dalje je gledala u vrata kroz koja je princ Andrej izašao i krstio ga. Iz radne sobe čuli su se, poput pucnjeva, često ponavljani ljutiti zvuci starca koji puše nos. Čim je princ Andrej otišao, vrata kancelarije su se brzo otvorila i napolje je pogledala stroga figura starca u belom mantilu.
- Levo? Pa, dobro! rekao je, ljutito gledajući u bezosjećajnu malu princezu, prijekorno odmahnuo glavom i zalupio vratima.

U oktobru 1805. godine ruske trupe zauzele su sela i gradove nadvojvodstva Austrije, a iz Rusije je stiglo još novih pukova i, opterećujući stanovnike smještajem, nalazilo se u blizini tvrđave Braunau. U Braunauu je bio glavni stan glavnog komandanta Kutuzova.
11. oktobra 1805. jedan od pješadijskih pukova koji je upravo stigao u Braunau, čekajući smotru glavnog komandanta, stajao je pola milje od grada. Uprkos neruskom terenu i situaciji (voćnjaci, kamene ograde, popločani krovovi, planine vidljive u daljini), neruski narod, koji je sa radoznalošću posmatrao vojnike, puk je imao potpuno isti izgled kao i svaki ruski puk koji se spremao za predstavu negde usred Rusije.

Jedinstvenost granice i ograničenosti konvergentnog numeričkog niza

Definicija 1 . Numerički niz (1) naziva se ograničenim ako skup članova ovog niza čini ograničeni skup.

U ovom slučaju, nazvat ćemo numerički niz (1) ograničena vrijednost.

Definicija 2 . Numerički niz (1) konvergira i ima ograničenje (Moguće je koristiti notaciju ) ako .

Ponovimo ovu definiciju, koristeći više ruskog jezika. Granica numeričkog niza postoji i jednaka je određenom broju ako su, počevši od određenog broja, svi članovi niza manji od bilo kojeg datog, proizvoljno malog pozitivnog broja, od ovog graničnog broja. Isto se može reći i drugim riječima. Broj će biti granica numeričkog niza (1) ako i samo ako za svako -okrug tačke svi članovi niza, počevši od nekog broja, leže u tom -susedstvu. Imajte na umu da se interval naziva -susjedstvo tačke.

Teorema 1 . Ako granica numeričkog niza postoji, onda je ona jedinstvena.

Dokaz . Dokažimo teoremu "metodom kontradikcije". Pretpostavimo da je teorema netačna i da postoje najmanje 2 broja i () za koje su ispunjeni uslovi Definicije 2. U ovoj definiciji uzimamo . Zatim, nakon broja, članovi niza se razlikuju od broja za manje od , a nakon broja, članovi niza se razlikuju od broja za manje od . Pokažimo da to ne može biti. U stvari, kod odnosi , , su zadovoljeni, odakle za ove imamo . Teorema je dokazana.

Teorema 2 . Ako brojčani niz ima ograničenje, tada je taj niz brojeva ograničen.

Dokaz . Dokaz će biti konstruktivan. Uzmimo i pronađimo odgovarajuće. Podijelimo niz na 2 dijela: prvi članovi i preostali članovi niza. Prva grupa se sastoji od konačnog broja članova i stoga je ograničena. Drugu grupu čine brojevi koji nisu udaljeni više od 1 od granične vrijednosti, pa je stoga i ograničen. Unija dva ograničena skupa je ograničen skup. Teorema je dokazana.

Beskonačno male količine i njihova svojstva

Definicija 3 . Poziva se brojčani niz beskrajno mali ako ima granicu jednaku 0.

Za beskonačno male veličine koristi se notacija b. m.

Neka su numerički nizovi i dati. Numerički niz sa zajedničkim pojmom naziva se zbir ovih numeričke sekvence. Numerički niz sa zajedničkim pojmom naziva se zbir ovih numeričkih nizova. Numerički niz sa zajedničkim pojmom naziva se zbir ovih numeričkih nizova.

Teorema 3 . Zbir konačnog broja infinitezimalnih veličina je beskonačno mala veličina.

Dokaz . Dovoljno je dokazati tvrdnju za zbir dva b. m. Neka su numerički nizovi i beskonačno male veličine, tj. granice ovih nizova su jednake 0. Ova činjenica znači sljedeće. Ako je dan proizvoljno mali pozitivni broj, tada za broj i numerički niz postoji broj koji ima svojstvo da za . Iz istog razloga, za isti broj i niz brojeva, postoji broj koji ima svojstvo da, za , odnos vrijedi. Uzmimo broj , zatim za . Dakle, za proizvoljan smo pronašli broj takav da kada . Prema tome, granica niza , jednaka je 0, i to je beskonačno mala veličina. Teorema je dokazana.

Teorema 4 . Proizvod beskonačno male količine na ograničenu količinu je beskonačno mala količina.

Dokaz . Neka je numerički niz beskonačno mala veličina, a numerički niz ograničena veličina. To znači da, s jedne strane, , S druge strane, postoji broj takav da je uvjet zadovoljen za svaki. Sada neka bude dat proizvoljan, skrolujući mali pozitivan broj. Razmotrimo broj , za njega u numeričkom nizu postoji broj koji ima svojstvo da relacija vrijedi za . U ovom slučaju, stanje , što znači da je proizvod ove dvije veličine - beskonačno male i ograničene - beskonačno mala veličina. Teorema je dokazana.

Ograničite svojstva

A kako je tačno izračunavanje granica, u ovom slučaju, numeričkih nizova? Pokušavamo da vrijednost, čija se granica mora naći, predstavimo kao zbir, razliku, proizvod, količnik jednostavnijih veličina čiju granicu je lako pronaći. Da bi se opravdao takav pristup, potrebno je formulisati i dokazati svojstva granica.

Teorema 5 . Brojčani niz ima ograničenje jednako ako i samo ako je niz, beskonačno mala vrijednost.

Dokaz . Neka , tj. za svaki za , nejednakost () je zadovoljena. Ali ova nejednakost je jednako pored toga , tj. sekvenca , ima ograničenje od 0, tj. je beskonačno mala količina. Teorema je dokazana. , gdje - b. m. Iz toga slijedi da . U posljednjoj zagradi, zbir dviju infinitezimalnih veličina je količina b. m. Stoga je predstavljen kao zbir i infinitezimalna vrijednost. Na osnovu teoreme 5, to znači da . Prva tvrdnja teoreme je dokazana. Formula se dokazuje na potpuno isti način. Razmotrite sada formulu i koristite istu notaciju za transformaciju lijeve strane. Zbog toga …

Daje se definicija infinitezimalnog niza. Ima svojstva konvergentnih nizova. Postoje i svojstva koja su karakteristična samo za nizove sa ograničenjem jednakim nuli. Dati su dokazi o takvim svojstvima. Razmatran je primjer u kojem je potrebno dokazati da je niz beskonačno mali.

Sadržaj

Definicija

Infinitezimalni niz (αn) je konvergentni niz čija je granica nula:
.

Sljedeća svojstva su direktna posljedica aritmetičkih svojstava, primijenjenih na nizove čija je granica nula.

Svojstvo zbira i razlike infinitezimalnih nizova

Zbir i razlika konačan broj infinitezimalnih nizova je infinitezimalni niz.
Također linearna kombinacija konačan broj infinitezimalnih nizova je infinitezimalni niz.
Dokaz granice zbira i razlike numeričkih nizova.

Svojstvo proizvoda infinitezimalnih nizova

Proizvod konačnog broja infinitezimalni nizovi je infinitezimalni niz.
Dokaz ograničenja proizvoda brojnih nizova.

Sljedeća svojstva primjenjuju se samo na infinitezimalne nizove i nisu direktna posljedica svojstava konvergentnih nizova.

( x n )
x n \u003d b + α n,
gdje (αn)

Property Proofs

Svojstvo proizvoda ograničenog niza infinitezimalom

Proizvod ograničenog niza na infinitezimalni je infinitezimalni niz.

Dokaz

Neka je niz ograničen nekim brojem:
(3.1) .

Neka je niz beskonačno mali. To jest, postoji takva funkcija ovisno o varijabli da je za bilo koju pozitivnu vrijednost varijable , nejednakost
(3.2) u .

Neka sekvenca bude proizvod nizova i . Njegov opšti pojam je:
.
Moramo pronaći funkciju koja zadovoljava nejednakost
(3.3) u .

Primjenjujemo (3.1) i (3.2):
.
Ovo se radi sa . dakle,
.
stavimo:
.

Odnosno, pronašli smo takvu funkciju, pod kojom, za bilo koji pozitivan broj, vrijedi sljedeća nejednakost:
(3.3) u .

Imovina je dokazana.

Svojstvo predstavljanja konvergentnog niza u terminima infinitezimalnog

U cilju redosleda ( x n ) ima granicu b , potrebno je i dovoljno da
x n \u003d b + α n,
gdje (αn) je beskonačno mali niz.

Dokaz

Need. Neka bude . Razmotrite niz sa zajedničkim pojmom. Koristimo aritmetička svojstva granica:
.
To jest, beskonačno mali niz.

Adekvatnost. Neka bude . Na osnovu aritmetičkih svojstava granica, imamo:
.

Imovina je dokazana.

Primjer

Svi primjeri Koristeći definiciju granice niza, dokazati da je niz

je beskonačno mali.

Pišemo definiciju infinitezimalnog niza:
.
Pošto je n prirodan broj, n = 1, 2, 3, ... , onda
,
,
.
Prema tome, članovi niza su pozitivni brojevi. Onda
.

Dakle, dobili smo sljedeći rezultat:
.
Enter pozitivni brojevi i :
.
Prema svojstvima nejednakosti , Ako i , Tada
.

Iz toga slijedi da se za bilo koje pozitivno može naći prirodni broj, dakle u ,
.
To znači da je granica originalnog niza nula i stoga je beskonačno mala.

BESKONAČNO MALE FUNKCIJE I NJIHOVA GLAVNA SVOJSTVA

Funkcija y=f(x) pozvao beskonačno mali at x→a ili kada x→∞ ako ili , tj. Infinitezimalna funkcija je funkcija čija je granica u datoj tački nula.

Primjeri.

Hajde da uspostavimo sledeću važnu relaciju:

Teorema. Ako je funkcija y=f(x) zastupljen na x→a kao zbir konstantnog broja b i beskonačno mali α(x): f(x)=b+ α(x) onda .

Obrnuto, ako , tada f(x)=b+α(x), gdje sjekira) je beskonačno mala pri x→a.

Dokaz.

Razmotrimo glavna svojstva infinitezimalnih funkcija.

Teorema 1. Algebarski zbir dva, tri i općenito bilo kojeg konačnog broja infinitezimala je infinitezimalna funkcija.

Dokaz. Dajemo dokaz za dva člana. Neka bude f(x)=α(x)+β(x), gdje i . Moramo dokazati da za proizvoljno mali ε > 0 tamo δ> 0, tako da za x zadovoljavanje nejednakosti |x – a|<δ , izvedeno |f(x)|< ε.

Pa da popravimo proizvoljan broj ε > 0. Pošto je, prema hipotezi teoreme, α(x) je infinitezimalna funkcija, onda postoji δ 1 > 0, koji u |x – a|< δ 1 imamo |α(x)|< ε / 2. Isto tako, pošto β(x) je beskonačno mala, onda postoji takav δ 2 > 0, koji u |x – a|< δ 2 imamo | β(x)|< ε / 2.

Uzmimo δ=min(δ1 , δ2 } .Onda u susjedstvu točke a radijus δ svaka od nejednakosti će biti zadovoljena |α(x)|< ε / 2 i | β(x)|< ε / 2. Dakle, u ovom naselju će ih biti

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,

one. |f(x)|< ε, što je trebalo dokazati.

Teorema 2. Proizvod infinitezimalne funkcije sjekira) za ograničenu funkciju f(x) at x→a(ili kada x→∞) je infinitezimalna funkcija.

Dokaz. Od funkcije f(x) je ograničen, onda postoji broj M tako da za sve vrijednosti x iz nekog susedstva tačke a|f(x)|≤M. Osim toga, pošto sjekira) je infinitezimalna funkcija za x→a, tada za proizvoljno ε > 0 postoji susjedstvo tačke a, u kojoj je nejednakost |α(x)|< ε /M. Zatim u manjem od ovih naselja koje imamo | αf|< ε /M= ε. A ovo znači to af- beskonačno mali. Za tu priliku x→∞ dokaz se izvodi na sličan način.

Iz dokazane teoreme slijedi:

Posljedica 1. Ako i , onda .

Posljedica 2. Ako i c= const, zatim .

Teorema 3. Omjer infinitezimalne funkcije α(x) po funkciji f(x), čija je granica različita od nule, je infinitezimalna funkcija.

Dokaz. Neka bude . Zatim 1 /f(x) postoji ograničena funkcija. Dakle, razlomak je proizvod infinitezimalne funkcije i ograničene funkcije, tj. funkcija je beskonačno mala.

ODNOS IZMEĐU BESKONAČNO MALIH I BESKONAČNO VELIKIH FUNKCIJA

Teorema 1. Ako je funkcija f(x) je beskonačno velika pri x→a, zatim funkcija 1 /f(x) je beskonačno mala pri x→a.

Dokaz. Uzmite proizvoljan broj ε >0 i pokazati to nekima δ>0 (u zavisnosti od ε) za sve x, za koji |x – a|<δ , nejednakost je zadovoljena, a to će značiti da 1/f(x) je infinitezimalna funkcija. Zaista, pošto f(x) je beskonačno velika funkcija za x→a, onda postoji δ>0 tako da čim |x – a|<δ , pa | f(x)|> 1/ ε. Ali onda za isto x.

Primjeri.

Obrnuta teorema se također može dokazati.

Teorema 2. Ako je funkcija f(x)- beskonačno mali u x→a(ili x→∞) i onda ne nestaje y= 1/f(x) je beskonačna funkcija.

Dokažite teoremu sami.

Primjeri.

Dakle, najjednostavnija svojstva beskonačno malih i beskonačno velikih funkcija mogu se napisati korištenjem sljedećih uvjetnih odnosa: A≠ 0

TEOREME O GRANICAMA

Teorema 1. Granica algebarskog zbira dvije, tri i općenito određenog broja funkcija jednaka je algebarskom zbiru granica ovih funkcija, tj.

Dokaz. Dokaz ćemo izvršiti za dva člana, jer se za bilo koji broj pojmova izvodi na isti način. Neka bude .Onda f(x)=b+α(x) I g(x)=c+β(x), gdje α I β su beskonačno male funkcije. shodno tome,

f(x) + g(x)=(b + c) + (α(x) + β(x)).

Jer b+c je konstanta, i α(x) + β(x) je onda infinitezimalna funkcija

Primjer. .

Teorema 2. Granica proizvoda dvije, tri i općenito konačnog broja funkcija jednaka je proizvodu granica ovih funkcija:

Dokaz. Neka bude . shodno tome, f(x)=b+α(x) I g(x)=c+β(x) I

fg = (b + α)(c + β) = bc + (bβ + cα + αβ).

Posao bc je konstantna vrijednost. Funkcija bβ + cα + αβ na osnovu svojstava infinitezimalnih funkcija, postoji infinitezimalna količina. Zbog toga .

Posljedica 1. Konstantni faktor se može izvaditi iz graničnog znaka:

Posljedica 2. Granica stepena je jednaka stepenu granice:

Primjer..

Teorema 3. Granica količnika dvije funkcije jednaka je količniku granica ovih funkcija ako je granica nazivnika različita od nule, tj.

Dokaz. Neka bude . shodno tome, f(x)=b+α(x) I g(x)=c+β(x), gdje α, β su beskonačno male. Uzmite u obzir količnik

Razlomak je beskonačno mala funkcija jer je brojnik beskonačno mala funkcija, a nazivnik ima ograničenje c2 ≠0.

Primjeri.

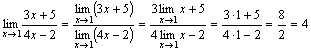
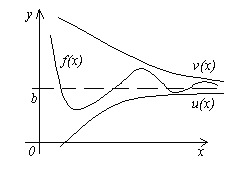
Teorema 4. Neka su date tri funkcije f(x), u(x) I v(x), zadovoljavajući nejednakosti u (x)≤f(x)≤v(x). Ako funkcije u(x) I v(x) imaju istu granicu x→a(ili x→∞), zatim funkciju f(x) teži istoj granici, tj. ako

, zatim .

Značenje ove teoreme jasno je iz slike.

Dokaz teoreme 4 može se naći, na primjer, u udžbeniku: Piskunov N. S. Diferencijalni i integralni račun, tom 1 - M.: Nauka, 1985.

Teorema 5. Ako na x→a(ili x→∞) funkcija y=f(x) uzima nenegativne vrijednosti y≥0 i teži krajnjim granicama b, tada ova granica ne može biti negativna: b≥0.

Dokaz. Dokaz će biti izveden kontradikcijom. Pretvarajmo se to b<0 , onda |y – b|≥|b| i, prema tome, modul razlike ne teži nuli na x→a. Ali onda y ne ide do krajnjih granica b at x→a, što je u suprotnosti sa uslovom teoreme.

Teorema 6. Ako dvije funkcije f(x) I g(x) za sve vrijednosti argumenta x zadovoljiti nejednakost f(x)≥ g(x) i imaju granice , tada imamo nejednakost b≥c.

Dokaz. Prema teoremi f(x)-g(x) ≥0, dakle, prema teoremi 5 , ili .

JEDNOSTRANE OGRANIČENJA

Do sada smo razmatrali definiciju granice funkcije kada x→a proizvoljno, tj. granica funkcije nije ovisila o tome kako je x prema a, lijevo ili desno od a. Međutim, prilično je uobičajeno pronaći funkcije koje nemaju ograničenja pod ovim uvjetom, ali imaju ograničenje ako x→a, ostajući na jednoj strani ali, lijevo ili desno (vidi sl.). Stoga se uvodi koncept jednostranih granica.

Ako f(x) teži krajnjim granicama b at x težeći nekom broju a tako x uzima samo vrijednosti manje od a, zatim pišite i pozovite kraj funkcije f(x) u tački a na lijevoj strani.