Az alapvető elemi függvények, az ezekben rejlő tulajdonságok és a hozzájuk tartozó gráfok a matematikai ismeretek egyik alapját képezik, jelentőségükben hasonlóak a szorzótáblához. Az elemi funkciók minden elméleti kérdés vizsgálatának alapját, támaszát jelentik.

Az alábbi cikk kulcsfontosságú anyagokat tartalmaz az alapvető elemi funkciók témakörében. Bevezetjük a kifejezéseket, meghatározzuk őket; Tanulmányozzuk részletesen az egyes elemi függvénytípusokat, és elemezzük tulajdonságaikat.

Az alapvető elemi függvények következő típusait különböztetjük meg:

1. definíció

• állandó függvény (konstans);
• n-edik fok gyökere;
• teljesítmény funkció;
• exponenciális függvény;
• logaritmikus függvény;
• trigonometrikus függvények;
• testvéri trigonometrikus függvények.

Egy konstans függvényt a következő képlet határoz meg: y = C (C valamilyen valós szám), és neve is van: konstans. Ez a függvény határozza meg, hogy az x független változó bármely valós értéke megfelel-e az y változó azonos értékének – a C értéknek.

Egy konstans grafikonja egy egyenes, amely párhuzamos az x tengellyel, és egy (0, C) koordinátájú ponton halad át. Az érthetőség kedvéért az y = 5, y = - 2, y = 3, y = 3 konstans függvények grafikonjait mutatjuk be (a rajzon feketével, pirossal és kékkel jelölve).

2. definíció

Ezt az elemi függvényt az y = x n (n - természetes szám több mint egy).

Tekintsük a függvény két változatát.

1. Az n-edik fokú gyöke, n páros szám

Az érthetőség kedvéért feltüntetjük a rajzot, amely az ilyen függvények grafikonjait mutatja: y = x , y = x 4 és y = x 8. Ezek a funkciók színkóddal vannak ellátva: fekete, piros és kék.

Hasonló nézet a páros fok függvényének grafikonjairól a mutató más értékeire vonatkozóan.

3. definíció

Az n-edik fokú függvénygyök tulajdonságai, n páros szám

• a definíciós tartomány az összes nem negatív halmaza valós számok [ 0 , + ∞) ;
• ha x = 0, a függvény y = x n értéke nulla;
• ez a függvény egy függvény Általános nézet(nem páros és nem páratlan);
• tartomány: [ 0 , + ∞) ;
• ez a függvény y = x n a gyöknövekedés páros kitevőjével a teljes definíciós tartományban;
• a függvénynek felfelé mutató konvexitása van a teljes definíciós tartományban;
• nincsenek inflexiós pontok;
• nincsenek aszimptoták;
• a függvény grafikonja páros n-re átmegy a (0 ; 0) és (1 ; 1) pontokon.

1. Az n-edik fok gyöke, n páratlan szám

Egy ilyen függvény a valós számok teljes halmazán definiálva van. Az érthetőség kedvéért vegyük figyelembe a függvénygrafikonokat y = x 3, y = x 5 és x 9. A rajzon színekkel jelöljük őket: a görbék fekete, piros és kék színei, ill.

Az y = x n függvény gyökének más páratlan értékei hasonló alakú grafikont adnak.

4. definíció

Az n-edik fokú függvénygyök tulajdonságai, n páratlan szám

• a definíciós tartomány az összes valós szám halmaza;
• ez a függvény páratlan;
• az értéktartomány az összes valós szám halmaza;
• az y = x n függvény a gyök páratlan kitevőjével növekszik a teljes definíciós tartományban;
• a függvénynek van konkávitása a (- ∞ ; 0 ] intervallumon és konvexitása a [ 0 , + ∞ ) intervallumon;
• az inflexiós pontnak vannak koordinátái (0 ; 0) ;
• nincsenek aszimptoták;
• a páratlan n függvény grafikonja átmegy a (- 1 ; - 1), (0 ; 0) és (1 ; 1) pontokon.

Teljesítmény funkció

5. definíció

A hatványfüggvényt az y = x a képlet határozza meg.

A grafikonok típusa és a függvény tulajdonságai a kitevő értékétől függenek.

• ha egy hatványfüggvény egész kitevője a, akkor a hatványfüggvény grafikonjának formája és tulajdonságai attól függnek, hogy a kitevő páros vagy páratlan, és attól is, hogy milyen előjelű a kitevő. Vizsgáljuk meg ezeket a különleges eseteket az alábbiakban részletesebben;
• a kitevő lehet tört vagy irracionális - ettől függően a gráfok típusa és a függvény tulajdonságai is változnak. A speciális eseteket több feltétel felállításával elemezzük: 0< a < 1 ; a > 1 ; - 1 < a < 0 и a < - 1 ;
• egy hatványfüggvénynek lehet nulla kitevője, az alábbiakban ezt az esetet is elemezzük részletesebben.

Elemezzük a hatványfüggvényt y = x a, ha a páratlan pozitív szám például a = 1 , 3 , 5 ...

Az érthetőség kedvéért feltüntetjük az ilyen hatványfüggvények grafikonjait: y = x (a grafikon fekete színe), y = x 3 (a diagram kék színe), y = x 5 (a grafikon piros színe), y = x 7 (zöld grafikon). Ha a = 1, akkor egy y = x lineáris függvényt kapunk.

6. definíció

Hatványfüggvény tulajdonságai, ha a kitevő páratlan pozitív

• a függvény növekszik x ∈ esetén (- ∞ ; + ∞) ;
• a függvény konvex x ∈ (- ∞ ; 0 ] esetén, és konkáv x ∈ [ 0 ; + ∞) esetén (a lineáris függvény nélkül);
• az inflexiós pontnak vannak koordinátái (0 ; 0) (a lineáris függvény nélkül);
• nincsenek aszimptoták;
• függvény átadási pontjai: (- 1 ; - 1) , (0 ; 0) , (1 ; 1) .

Elemezzük a hatványfüggvényt y = x a, ha a páros pozitív szám, például a = 2 , 4 , 6 ...

Az érthetőség kedvéért feltüntetjük az ilyen hatványfüggvények grafikonjait: y \u003d x 2 (a grafikon fekete színe), y = x 4 (a grafikon kék színe), y = x 8 (a grafikon piros színe). Ha a = 2, akkor egy másodfokú függvényt kapunk, amelynek grafikonja egy másodfokú parabola.

7. definíció

Hatványfüggvény tulajdonságai, ha a kitevő páros pozitív:

• definíciós tartomány: x ∈ (- ∞ ; + ∞) ;
• csökkenő x ∈ esetén (- ∞ ; 0 ] ;
• a függvény konkáv x ∈ (- ∞ ; + ∞) esetén;
• nincsenek inflexiós pontok;
• nincsenek aszimptoták;
• függvény átadási pontjai: (- 1 ; 1) , (0 ; 0) , (1 ; 1) .

Az alábbi ábra példákat mutat be exponenciális függvénygrafikonokra y = x a, ha a páratlan negatív szám: y = x - 9 (a diagram fekete színe); y = x - 5 (a grafikon kék színe); y = x - 3 (a diagram piros színe); y = x - 1 (zöld grafikon). Ha a \u003d - 1, akkor egy fordított arányosságot kapunk, amelynek grafikonja egy hiperbola.

8. definíció

A hatványfüggvény tulajdonságai, ha a kitevő páratlan negatív:

Ha x \u003d 0, akkor egy második típusú szakadást kapunk, mivel lim x → 0 - 0 xa \u003d - ∞, lim x → 0 + 0 xa \u003d + ∞ a \u003d - 1, - 3, - esetén 5, .... Így az x = 0 egyenes függőleges aszimptota;

• tartomány: y ∈ (- ∞ ; 0) ∪ (0 ; + ∞) ;
• a függvény páratlan, mert y (- x) = - y (x) ;
• a függvény x ∈ - ∞ esetén csökken; 0 ∪ (0 ; + ∞);
• a függvény konvex x ∈ (- ∞ ; 0) esetén és konkáv x ∈ (0 ; + ∞) esetén;
• nincsenek inflexiós pontok;

k = lim x → ∞ x a x = 0, b = lim x → ∞ (x a - k x) = 0 ⇒ y = k x + b = 0, ha a = - 1 , - 3 , - 5 , . . . .

• függvény átadási pontjai: (- 1 ; - 1) , (1 ; 1) .

Az alábbi ábra példákat mutat be az y = x a hatványfüggvény grafikonjaira, amikor a páros negatív szám: y = x - 8 (fekete diagram); y = x - 4 (a grafikon kék színe); y = x - 2 (a grafikon piros színe).

9. definíció

A hatványfüggvény tulajdonságai, ha a kitevő páros negatív:

• definíciós tartomány: x ∈ (- ∞ ; 0) ∪ (0 ; + ∞) ;

Ha x \u003d 0, akkor egy második típusú szakadást kapunk, mivel lim x → 0 - 0 xa \u003d + ∞, lim x → 0 + 0 xa \u003d + ∞ a \u003d - 2, - 4, - esetén 6, .... Így az x = 0 egyenes függőleges aszimptota;

• a függvény páros, mert y (- x) = y (x) ;
• a függvény növekszik x ∈ (- ∞ ; 0) esetén, és csökken x ∈ 0 esetén; +∞ ;
• a függvény konkáv x ∈ (- ∞ ; 0) ∪ (0 ; + ∞) esetén;
• nincsenek inflexiós pontok;
• a vízszintes aszimptota egy egyenes y = 0, mert:

k = lim x → ∞ x a x = 0, b = lim x → ∞ (x a - k x) = 0 ⇒ y = k x + b = 0, ha a = - 2 , - 4 , - 6 , . . . .

• függvény átadási pontjai: (- 1 ; 1) , (1 ; 1) .

Már az elején ügyeljen a következő szempontra: abban az esetben, ha a páratlan nevezőjű pozitív tört, egyes szerzők a -∞ intervallumot veszik ennek a hatványfüggvénynek a definíciós tartományának; + ∞ , ami azt jelenti, hogy az a kitevő irreducibilis tört. Jelenleg számos algebráról és az elemzés kezdeteiről szóló oktatási publikáció szerzői NEM DEFINÍCIÓK teljesítmény függvények, ahol a kitevő az argumentum negatív értékeinek páratlan nevezőjével rendelkező tört. A továbbiakban csak egy ilyen állásponthoz ragaszkodunk: vesszük a halmazt [ 0 ; +∞) . Javaslat a tanulóknak: a nézeteltérések elkerülése érdekében ezen a ponton tájékozódjon a tanár álláspontjáról.

Tehát vessünk egy pillantást a teljesítmény függvényre y = x a, ha a kitevő racionális vagy irracionális szám, feltéve, hogy 0< a < 1 .

Szemléltessük grafikonokkal a hatványfüggvényeket y = x a, ha a = 11 12 (fekete diagram); a = 5 7 (a grafikon piros színe); a = 1 3 (a grafikon kék színe); a = 2 5 (a grafikon zöld színe).

Az a kitevő egyéb értékei (0-t feltételezve< a < 1) дадут аналогичный вид графика.

10. definíció

Hatványfüggvény tulajdonságai 0-nál< a < 1:

• tartomány: y ∈ [ 0 ; +∞) ;
• a függvény növekszik x ∈ [ 0 ; +∞) ;
• a függvénynek van konvexitása x ∈ (0 ; + ∞) esetén;
• nincsenek inflexiós pontok;
• nincsenek aszimptoták;

Elemezzük a hatványfüggvényt y = x a, ha a kitevő nem egész racionális vagy irracionális szám, feltéve, hogy a > 1 .

A hatványfüggvény grafikonjait szemléltetjük y = xa adott feltételek mellett az ilyen függvények példáján: y = x 5 4, y = x 4 3, y = x 7 3, y = x 3 π (a grafikonok fekete, piros, kék, zöld színe) .

Az a kitevő egyéb értékei a > 1 feltétel mellett hasonló képet adnak a grafikonról.

11. meghatározás

Hatványfüggvény tulajdonságai > 1 esetén:

• definíciós tartomány: x ∈ [ 0 ; +∞) ;
• tartomány: y ∈ [ 0 ; +∞) ;
• ez a függvény általános forma függvénye (nem páratlan és nem páratlan);
• a függvény növekszik x ∈ [ 0 ; +∞) ;
• a függvény konkáv x ∈ (0 ; + ∞) esetén (amikor 1< a < 2) и выпуклость при x ∈ [ 0 ; + ∞) (когда a > 2);
• nincsenek inflexiós pontok;
• nincsenek aszimptoták;
• függvény áthaladási pontjai: (0 ; 0) , (1 ; 1) .

Ha a páratlan nevezővel rendelkező negatív tört, akkor egyes szerzők munkáiban az a nézet, hogy a definíciós tartomány ebben az esetben a - ∞ intervallum; 0 ∪ (0 ; + ∞) azzal a feltétellel, hogy az a kitevő irreducibilis tört. Jelen pillanatban a szerzők tananyagok Az algebra és az elemzés kezdetei szerint a hatványfüggvények, amelyek kitevője páratlan nevezőjű tört formájában van, az argumentum negatív értékeivel NINCS DEFINÍCIÓ. Továbbá éppen egy ilyen nézethez ragaszkodunk: a (0 ; + ∞) halmazt vesszük a tört negatív kitevővel rendelkező hatványfüggvények tartományának. Javaslat a tanulóknak: Ezen a ponton tisztázza tanára elképzelését, hogy elkerülje a nézeteltéréseket.

Folytatjuk a témát és elemezzük a hatványfüggvényt y = x a feltéve: - 1< a < 0 .

Itt van a grafikonok rajza következő funkciók: y = x - 5 6, y = x - 2 3, y = x - 1 2 2, y = x - 1 7 (rendre fekete, piros, kék, zöld vonalak).

12. definíció

A teljesítményfüggvény tulajdonságai - 1-nél< a < 0:

lim x → 0 + 0 x a = + ∞, ha -1< a < 0 , т.е. х = 0 – вертикальная асимптота;

• tartomány: y ∈ 0 ; +∞ ;
• ez a függvény általános forma függvénye (nem páratlan és nem páratlan);
• nincsenek inflexiós pontok;

Az alábbi rajz az y = x - 5 4 , y = x - 5 3 , y = x - 6 , y = x - 24 7 hatványfüggvények grafikonjait mutatja (fekete, piros, kék, zöld színek görbék, ill.

13. definíció

Hatványfüggvény tulajdonságai a< - 1:

• definíciós tartomány: x ∈ 0 ; +∞ ;

lim x → 0 + 0 x a = + ∞ ha a< - 1 , т.е. х = 0 – вертикальная асимптота;

• tartomány: y ∈ (0 ; + ∞) ;
• ez a függvény általános forma függvénye (nem páratlan és nem páratlan);
• a függvény x ∈ 0 esetén csökken; +∞ ;
• a függvény konkáv x ∈ 0 esetén; +∞ ;
• nincsenek inflexiós pontok;
• vízszintes aszimptota - egyenes y = 0 ;
• függvény áthaladási pontja: (1 ; 1) .

Ha a \u003d 0 és x ≠ 0, akkor az y \u003d x 0 \u003d 1 függvényt kapjuk, amely meghatározza azt az egyenest, amelyből a (0; 1) pont ki van zárva (megegyeztünk, hogy a 0 0 kifejezést nem adjuk meg bármilyen érték).

Az exponenciális függvénynek van formája y = a x, ahol a > 0 és a ≠ 1, és ennek a függvénynek a grafikonja másképp néz ki az a bázis értéke alapján. Nézzünk speciális eseteket.

Nézzük először azt a helyzetet, amikor az alap exponenciális függvényértéke nullától egyig (0< a < 1) . Szemléltető példa az a = 1 2 (a görbe kék színe) és a = 5 6 (a görbe piros színe) függvénygrafikonjai.

Az exponenciális függvény grafikonjai hasonló formájúak lesznek az alap többi értékére is, feltéve, hogy 0< a < 1 .

14. definíció

Egy exponenciális függvény tulajdonságai, ha az alap kisebb egynél:

• tartomány: y ∈ (0 ; + ∞) ;
• ez a függvény általános forma függvénye (nem páratlan és nem páratlan);
• egy exponenciális függvény, amelynek bázisa kisebb, mint egy, a teljes definíciós tartományban csökken;
• nincsenek inflexiós pontok;
• a vízszintes aszimptota az y = 0 egyenes, ahol az x változó + ∞ -re hajlik;

Tekintsük most azt az esetet, amikor az exponenciális függvény bázisa nagyobb egynél (a > 1).

Illusztráljuk ezt a speciális esetet az y = 3 2 x (a görbe kék színe) és az y = e x (a gráf piros színe) exponenciális függvények grafikonjával.

A bázis egyéb értékei, amelyek egynél nagyobbak, hasonló képet adnak az exponenciális függvény grafikonjáról.

15. definíció

Az exponenciális függvény tulajdonságai, ha a bázis nagyobb egynél:

• a definíciós tartomány a valós számok teljes halmaza;
• tartomány: y ∈ (0 ; + ∞) ;
• ez a függvény általános forma függvénye (nem páratlan és nem páratlan);
• egy exponenciális függvény, amelynek bázisa nagyobb, mint egy, növekszik x ∈ - ∞ esetén; +∞ ;
• a függvény konkáv x ∈ - ∞ esetén; +∞ ;
• nincsenek inflexiós pontok;
• vízszintes aszimptota - egyenes y = 0, x változóval - ∞;
• függvény áthaladási pontja: (0 ; 1) .

A logaritmikus függvény alakja y = log a (x) , ahol a > 0, a ≠ 1 .

Egy ilyen függvény csak az argumentum pozitív értékeire van definiálva: x ∈ 0 esetén; +∞ .

A logaritmikus függvény grafikonja más alakú, az a bázis értéke alapján.

Tekintsük először azt a helyzetet, amikor 0< a < 1 . Продемонстрируем этот частный случай графиком логарифмической функции при a = 1 2 (синий цвет кривой) и а = 5 6 (красный цвет кривой).

A bázis egyéb értékei, amelyek nem nagyobbak egynél, hasonló képet adnak a grafikonról.

16. definíció

A logaritmikus függvény tulajdonságai, ha az alap kisebb egynél:

• definíciós tartomány: x ∈ 0 ; +∞ . Mivel x jobbról nullára tart, a függvény értékei + ∞;
• tartomány: y ∈ - ∞ ; +∞ ;
• ez a függvény általános forma függvénye (nem páratlan és nem páratlan);
• logaritmikus
• a függvény konkáv x ∈ 0 esetén; +∞ ;
• nincsenek inflexiós pontok;
• nincsenek aszimptoták;

Most elemezzünk egy speciális esetet, amikor a logaritmikus függvény alapja nagyobb egynél: a > 1 . Az alábbi rajzon y = log 3 2 x és y = ln x logaritmikus függvények grafikonjai (a grafikonok kék és piros színe) láthatók.

Az egynél nagyobb alapértékek hasonló képet adnak a grafikonról.

17. definíció

A logaritmikus függvény tulajdonságai, ha az alap nagyobb egynél:

• definíciós tartomány: x ∈ 0 ; +∞ . Mivel x jobbról nullára hajlik, a függvény értékei - ∞;
• tartomány: y ∈ - ∞ ; + ∞ (a valós számok teljes halmaza);
• ez a függvény általános forma függvénye (nem páratlan és nem páratlan);
• a logaritmikus függvény növekszik x ∈ 0 esetén; +∞ ;
• a függvénynek van konvexitása x ∈ 0 esetén; +∞ ;
• nincsenek inflexiós pontok;
• nincsenek aszimptoták;
• függvény áthaladási pontja: (1 ; 0) .

A trigonometrikus függvények szinusz, koszinusz, érintő és kotangens. Elemezzük mindegyik tulajdonságait és a megfelelő gráfokat.

Általában minden trigonometrikus függvényt a periodicitás tulajdonsága jellemez, pl. amikor a függvényértékek ismétlődnek különböző jelentések argumentum, amelyek az f (x + T) = f (x) periódus értékével különböznek egymástól (T a periódus). Így a trigonometrikus függvények tulajdonságainak listájához hozzáadódik a „legkisebb pozitív periódus” elem. Ezenkívül az argumentum azon értékeit fogjuk jelezni, amelyeknél a megfelelő függvény eltűnik.

1. Szinuszfüggvény: y = sin(x)

Ennek a függvénynek a grafikonját szinuszhullámnak nevezzük.

18. meghatározás

A szinuszfüggvény tulajdonságai:

• definíciós tartomány: a valós számok teljes halmaza x ∈ - ∞ ; +∞ ;
• a függvény eltűnik, ha x = π k, ahol k ∈ Z (Z az egész számok halmaza);
• a függvény növekszik x ∈ - π 2 + 2 π · k esetén; π 2 + 2 π k , k ∈ Z és csökkenő x ∈ π 2 + 2 π k esetén; 3 π 2 + 2 π k, k ∈ Z;
• a szinuszfüggvény rendelkezik helyi maximumok a π 2 + 2 π · k pontokban; 1 és helyi minimumok a pontokban - π 2 + 2 π · k ; - 1, k ∈ Z;
• a szinuszfüggvény konkáv, ha x ∈ - π + 2 π k; 2 π k , k ∈ Z és konvex, ha x ∈ 2 π k ; π + 2 π k, k ∈ Z;
• nincsenek aszimptoták.

1. koszinusz függvény: y=cos(x)

Ennek a függvénynek a grafikonját koszinuszhullámnak nevezzük.

19. meghatározás

A koszinusz függvény tulajdonságai:

• definíciós tartomány: x ∈ - ∞ ; +∞ ;
• a legkisebb pozitív periódus: T \u003d 2 π;
• tartomány: y ∈ - 1 ; egy ;
• ez a függvény páros, mivel y (- x) = y (x) ;
• a függvény növekszik x ∈ - π + 2 π · k esetén; 2 π · k , k ∈ Z és csökkenő x ∈ 2 π · k esetén; π + 2 π k, k ∈ Z;
• a koszinuszfüggvény lokális maximumokkal rendelkezik a 2 π · k pontokban; 1, k ∈ Z és lokális minimumok a π + 2 π · k pontokban; - 1, k ∈ z;
• a koszinuszfüggvény konkáv, ha x ∈ π 2 + 2 π · k ; 3 π 2 + 2 π k, k ∈ Z és konvex, ha x ∈ - π 2 + 2 π k; π 2 + 2 π · k , k ∈ Z ;
• Az inflexiós pontok koordinátái π 2 + π · k ; 0, k ∈ Z
• nincsenek aszimptoták.

1. Érintő függvény: y = t g (x)

Ennek a függvénynek a grafikonját ún tangentoid.

20. definíció

Az érintőfüggvény tulajdonságai:

• definíciós tartomány: x ∈ - π 2 + π · k ; π 2 + π k, ahol k ∈ Z (Z az egész számok halmaza);
• Az érintőfüggvény viselkedése a lim x → π 2 + π · k + 0 tg (x) = - ∞ , lim x → π 2 + π · k - 0 tg (x) = + definíciós tartomány határán ∞ . Így az x = π 2 + π · k k ∈ Z egyenesek függőleges aszimptoták;
• a függvény eltűnik, ha x = π k k ∈ Z esetén (Z az egész számok halmaza);
• tartomány: y ∈ - ∞ ; +∞ ;
• ez a függvény páratlan, mert y (- x) = - y (x) ;
• a függvény növekszik -π 2 + π · k esetén; π 2 + π k, k ∈ Z;
• az érintőfüggvény konkáv x ∈ [ π · k esetén; π 2 + π k) , k ∈ Z és konvex x ∈ esetén (- π 2 + π k ; π k ] , k ∈ Z ;
• Az inflexiós pontok koordinátái π k; 0, k ∈ Z;

1. Kotangens függvény: y = c t g (x)

Ennek a függvénynek a grafikonját kotangentoidnak nevezzük. .

21. meghatározás

A kotangens függvény tulajdonságai:

• definíciós tartomány: x ∈ (π k ; π + π k) , ahol k ∈ Z (Z az egész számok halmaza);

A kotangens függvény viselkedése a lim x → π · k + 0 t g (x) = + ∞ definíciós tartomány határán, lim x → π · k - 0 t g (x) = - ∞ . Így az x = π k k ∈ Z egyenesek függőleges aszimptoták;

• a legkisebb pozitív periódus: T \u003d π;
• a függvény eltűnik, ha x = π 2 + π k k ∈ Z esetén (Z az egész számok halmaza);
• tartomány: y ∈ - ∞ ; +∞ ;
• ez a függvény páratlan, mert y (- x) = - y (x) ;
• a függvény csökkenőben van x ∈ π · k esetén; π + π k, k ∈ Z;
• a kotangens függvény konkáv x ∈ (π k ; π 2 + π k ] , k ∈ Z esetén és konvex x ∈ [ - π 2 + π k ; π k ; π k ), k ∈ Z esetén;
• Az inflexiós pontok koordinátái π 2 + π · k ; 0, k ∈ Z;
• nincsenek ferde és vízszintes aszimptoták.

Az inverz trigonometrikus függvények az arcszinusz, arkkoszinusz, arctangens és arckotangens. Gyakran az "ív" előtag jelenléte miatt a névben az inverz trigonometrikus függvényeket ívfüggvényeknek nevezik. .

1. Arcsinuszfüggvény: y = a r c sin (x)

22. definíció

Az arcszinusz függvény tulajdonságai:

• ez a függvény páratlan, mert y (- x) = - y (x) ;
• az arcszinuszfüggvény konkáv x ∈ 0 esetén; 1 és konvexitás x ∈ - 1 esetén; 0;
• az inflexiós pontok koordinátái (0 ; 0) , ez egyben a függvény nullája is;
• nincsenek aszimptoták.

1. Arccosine funkció: y = a r c cos (x)

23. definíció

Arccosine függvény tulajdonságai:

• definíciós tartomány: x ∈ - 1 ; egy ;
• tartomány: y ∈ 0 ; π;
• ez a függvény általános formájú (sem páros, sem nem páratlan);
• a függvény a teljes definíciós tartományban csökken;
• az arccosinus függvény konkáv x ∈ - 1 esetén; 0 és konvexitás x ∈ 0 esetén; egy ;
• Az inflexiós pontok koordinátái 0 ; π2;
• nincsenek aszimptoták.

1. Arktangens függvény: y = a r c t g (x)

24. definíció

Arktangens függvény tulajdonságai:

• definíciós tartomány: x ∈ - ∞ ; +∞ ;
• tartomány: y ∈ - π 2 ; π2;
• ez a függvény páratlan, mert y (- x) = - y (x) ;
• a függvény növekszik a teljes definíciós tartományban;
• az arctangens függvény konkáv x ∈ (- ∞ ; 0 ] esetén és konvex x ∈ [ 0 ; + ∞ ) esetén;
• az inflexiós pontnak vannak koordinátái (0; 0), ez egyben a függvény nullája is;
• A vízszintes aszimptoták az y = - π 2 egyenesek x → - ∞ esetén és y = π 2 x → + ∞ esetén (az ábrán az aszimptoták zöld vonalak).

1. Ív kotangens függvény: y = a r c c t g (x)

25. meghatározás

Az ívkotangens függvény tulajdonságai:

• definíciós tartomány: x ∈ - ∞ ; +∞ ;
• tartomány: y ∈ (0 ; π) ;
• ez a funkció általános típusú;
• a függvény a teljes definíciós tartományban csökken;
• az arc kotangens függvény konkáv x ∈ [ 0 ; + ∞) és konvexitás x ∈ esetén (- ∞ ; 0 ] ;
• az inflexiós pont koordinátái 0 ; π2;
• vízszintes aszimptoták az y = π egyenesek x → - ∞ (zöld vonal a rajzon) és y = 0 x → + ∞ pontban.

Ha hibát észlel a szövegben, jelölje ki, és nyomja meg a Ctrl+Enter billentyűkombinációt

Teljesítmény funkció. Ez a funkció: y = ax n, ahol a,n- állandó. Nál nél n= 1-et kapunk egyenes arányosság: y = fejsze; nál nél n = 2 - négyzet alakú parabola ; nál nél n = - 1 - fordított arányosság vagy túlzás. Így ezek a függvények egy hatványfüggvény speciális esetei. Tudjuk, hogy bármely nem nulla szám nulla hatványa az 1, tehát at n= 0 a hatványfüggvény állandóvá válik:y = a, azaz e. az ő menetrendje egyenes, tengelye párhuzamos x, kivéve az eredetet (pontosíts kérlek, miért ? ). Mindezek az esetek (val a= 1 ) ábrán látható.13 (n 0 ) és 14. ábra ( n < 0). Отрицательные значения xitt nem veszik figyelembe például néhány funkció:

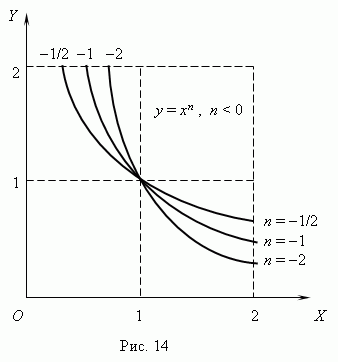
Ha n– teljes, hatalmi függvényeknek akkor is van értelmex< 0, но их графики имеют различный вид в зависимости от того, является ли npáros vagy páratlan szám. A 15. ábra két ilyen teljesítményfüggvényt mutat be: számára n= 2 és n = 3.


Nál nél n= 2 függvény páros ésgrafikonja szimmetrikus a tengelyről Y. Nál nél n= 3 a függvény páratlan és grafikonja szimmetrikus az origóhoz képest koordináták. Funkcióy = x 3 hívott köbös parabola.

A 16. ábra a funkciót mutatja. Ez funkció az inverz négyzetparabola y = x 2 , grafikonját a grafikon elforgatásával kapjuk meg négyzet alakú parabola az 1. koordinátaszög felezője körül. Ez egy módja annak, hogy bármilyen grafikont készítsen inverz függvény eredeti függvényének grafikonjából. A grafikonon láthatjuk, hogy ez egy kétértékű függvény (ezt a ± jel is jelzi négyzetgyök). Az ilyen függvényeket az elemi matematikában nem tanulmányozzák, ezért függvényként általában annak egyik ágát tekintjük: felsőt vagy alsót.

Először próbálja meg megtalálni a funkció hatókörét:

Sikerült? Hasonlítsuk össze a válaszokat:

Rendben? Szép munka!

Most próbáljuk meg megtalálni a függvény tartományát:

Megtalált? Összehasonlítás:

Megegyezett? Szép munka!

Dolgozzunk újra a grafikonokkal, csak most egy kicsit nehezebb - megtalálni a függvény tartományát és a függvény tartományát is.

Hogyan lehet megtalálni a tartományt és a funkció tartományát (speciális)

Íme, mi történt:

A grafikával szerintem rájöttél. Most próbáljuk meg megtalálni a függvény tartományát a képletekkel összhangban (ha nem tudja, hogyan kell ezt megtenni, olvassa el az erről szóló részt):

Sikerült? Ellenőrzés válaszol:

1. , mivel a gyökérkifejezésnek nullánál nagyobbnak vagy egyenlőnek kell lennie.
2. , mivel nem lehet nullával osztani, és a gyök kifejezés nem lehet negatív.
3. , hiszen, illetve mindenre.
4. mert nullával nem lehet osztani.

Van azonban még egy pillanat, amit még nem sikerült megoldani...

Hadd ismételjem meg a meghatározást, és összpontosítsak rá:

Megjegyezte? A „csak” szó nagyon-nagyon fontos eleme definíciónknak. Megpróbálom az ujjakon elmagyarázni.

Tegyük fel, hogy van egy egyenes által adott függvényünk. . Amikor ezt az értéket behelyettesítjük a "szabályunkba", és megkapjuk azt. Egy érték egy értéknek felel meg. Akár egy táblázatot is készíthetünk különféle értékekből, és ennek ellenőrzésére ábrázolhatunk egy adott függvényt.

"Néz! - azt mondod - "" kétszer találkozik!" Tehát lehet, hogy a parabola nem függvény? Nem, ez!

Az a tény, hogy a "" kétszer fordul elő, korántsem ok arra, hogy a parabolát kétértelműséggel vádoljuk!

A helyzet az, hogy a számítás során egy meccset kaptunk. És ha ezzel számolunk, egy játékot kaptunk. Tehát ez így van, a parabola egy függvény. Nézd meg a táblázatot:

Megvan? Ha nem, akkor itt van egy valós példa számodra, messze a matematikától!

Tegyük fel, hogy van egy csoport pályázónk, akik találkoztak a dokumentumok benyújtásakor, és mindegyikük egy beszélgetés során elmondta, hol él:

Egyetértek, teljesen valós, hogy több srác él ugyanabban a városban, de lehetetlen, hogy egy ember egyszerre több városban éljen. Ez mintegy logikus ábrázolása a "parabolánknak" - Ugyanannak az y-nek több különböző x felel meg.

Most jöjjön egy példa, ahol a függőség nem függvény. Tegyük fel, hogy ugyanezek a srácok elmondták, milyen szakokra jelentkeztek:

Nálunk teljesen más a helyzet: egy ember könnyedén jelentkezhet egy vagy több irányra. Azaz egy elemet készletek kerülnek levelezésbe több elem készletek. Illetőleg, ez nem funkció.

Teszteljük tudásunkat a gyakorlatban.

Határozza meg a képek alapján, hogy mi a függvény és mi nem:

Megvan? És itt van válaszol:

• A függvény - B,E.
• Nem függvény - A, B, D, D.

Kérded miért? Igen, ezért:

Minden ábrán, kivéve BAN BEN)És E) több van egyért!

Biztos vagyok benne, hogy most könnyen meg lehet különböztetni egy függvényt a nem függvénytől, megmondhatja, mi az argumentum és mi a függő változó, valamint meghatározhatja az argumentum és a függvény hatókörét. Térjünk át a következő részre – hogyan definiáljunk függvényt?

A funkció beállításának módjai

Mit gondolsz, mit jelentenek a szavak "beállítás funkció"? Így van, ez azt jelenti, hogy mindenkinek el kell magyarázni, hogy ebben az esetben milyen funkcióról beszélünk. Sőt, úgy magyarázd, hogy mindenki jól értsen, és az emberek által a te magyarázatod szerint rajzolt függvénygrafikonok ugyanazok legyenek.

Hogyan tudom ezt megtenni? Hogyan állítsunk be egy funkciót? A legegyszerűbb módja, amelyet ebben a cikkben már többször használtak - képlet segítségével.Írunk egy képletet, és egy értéket behelyettesítve kiszámoljuk az értéket. És amint emlékszel, a képlet egy törvény, egy szabály, amely szerint számunkra és egy másik személy számára is világossá válik, hogyan válik X-ből Y.

Általában pontosan ezt csinálják - a feladatokban képletekkel definiált kész függvényeket látunk, de vannak más módok is a függvény beállítására, amiről mindenki megfeledkezik, és ezért felvetődik a „hogyan tud még beállítani egy függvényt?” összezavarja. Nézzünk meg mindent sorban, és kezdjük az elemzési módszerrel.

A függvény meghatározásának analitikus módja

Az analitikai módszer egy függvény feladata egy képlet segítségével. Ez a leguniverzálisabb, legátfogóbb és legegyértelműbb módszer. Ha van képlete, akkor abszolút mindent tud a függvényről - készíthet rajta értéktáblázatot, készíthet grafikont, meghatározhatja, hol nő és hol csökken a függvény, általában, fedezze fel. teljesen.

Tekintsünk egy függvényt. mit számít?

"Mit jelent?" - kérdezed. most elmagyarázom.

Hadd emlékeztesselek arra, hogy a jelölésben a zárójelben lévő kifejezést argumentumnak nevezzük. Ez az érv pedig bármilyen kifejezés lehet, nem feltétlenül egyszerű. Ennek megfelelően, bármilyen legyen is az argumentum (zárójelben lévő kifejezés), azt írjuk be a kifejezésbe.

Példánkban ez így fog kinézni:

Vegyünk egy másik feladatot, amely a vizsgán megjelenő funkció meghatározásának analitikai módszeréhez kapcsolódik.

Keresse meg a kifejezés értékét, at.

Biztos vagyok benne, hogy először megijedtél, amikor megláttál egy ilyen kifejezést, de semmi ijesztő nincs benne!

Minden ugyanaz, mint az előző példában: bármi legyen is az argumentum (zárójelben lévő kifejezés), azt írjuk be a kifejezésbe. Például egy funkcióhoz.

Mit kell tenni a példánkban? Ehelyett írnod ​​kell, és a - helyett:

rövidítse le a kapott kifejezést:

Ez minden!

Önálló munkavégzés

Most próbálja meg saját maga megtalálni a következő kifejezések jelentését:

1. , ha
2. , ha

Sikerült? Hasonlítsuk össze a válaszainkat: Megszoktuk, hogy a függvénynek van formája

Példánkban is így definiáljuk a függvényt, de analitikusan lehetséges például implicit módon is definiálni a függvényt.

Próbálja meg saját maga megépíteni ezt a funkciót.

Sikerült?

Így építettem fel.

Milyen egyenlethez jutottunk?

Jobb! Lineáris, ami azt jelenti, hogy a grafikon egy egyenes lesz. Készítsünk egy táblázatot annak meghatározására, hogy mely pontok tartoznak a vonalunkhoz:

Éppen erről beszéltünk... Egy többnek felel meg.

Próbáljuk meg lerajzolni, mi történt:

Funkciója van annak, amit kaptunk?

Így van, nem! Miért? Próbálj meg egy kép segítségével válaszolni erre a kérdésre. Mit kaptál?

"Mert egy érték több értéknek felel meg!"

Milyen következtetést vonhatunk le ebből?

Így van, egy függvény nem mindig fejezhető ki kifejezetten, és ami függvénynek van "álcázva", az nem mindig függvény!

A függvény meghatározásának táblázatos módja

Ahogy a neve is sugallja, ez a módszer egy egyszerű lemez. Igen igen. Mint amit már készítettünk. Például:

Itt azonnal észrevett egy mintát - Y háromszor nagyobb, mint X. És most a „gondolkozz nagyon jól” feladat: szerinted egy táblázat formájában megadott függvény egyenértékű a függvénnyel?

Ne beszéljünk sokáig, hanem rajzoljunk!

Így. Mindkét módon adott függvényt rajzolunk:

Látod a különbséget? Nem a megjelölt pontokról van szó! Nézze meg közelebbről:

most láttad? Amikor táblázatos módon állítjuk be a függvényt, akkor a grafikonon csak azokat a pontokat tükrözzük, amelyek a táblázatban szerepelnek, és az egyenes (mint esetünkben) csak rajtuk halad át. Amikor egy függvényt analitikus módon definiálunk, tetszőleges pontot vehetünk, és a funkciónk nem korlátozódik ezekre. Itt van egy ilyen funkció. Emlékezik!

Grafikus módszer egy függvény felépítésére

Grafikus mód függvény összeállítása nem kevésbé kényelmes. Megrajzoljuk a függvényünket, és egy másik érdeklődő megtalálja, hogy y mi egyenlő egy bizonyos x-nél, és így tovább. A grafikus és analitikai módszerek a leggyakoribbak.

Itt azonban emlékezni kell arra, amiről a legelején beszéltünk - nem minden koordináta-rendszerben megrajzolt „pörgés” függvény! Emlékezett? Minden esetre idemásolom a függvény meghatározását:

Általában az emberek általában pontosan azt a három módszert nevezik meg a függvény megadásának, amelyet elemeztünk - analitikus (képlet segítségével), táblázatos és grafikus, teljesen megfeledkezve arról, hogy egy függvény leírható szóban is. Mint ez? Igen, nagyon könnyű!

A funkció szóbeli leírása

Hogyan írjuk le a funkciót szóban? Vegyük a legutóbbi példánkat - . Ez a funkció leírható: "x minden valós értéke a hármas értékének felel meg". Ez minden. Semmi bonyolult. Természetesen tiltakozik majd - „vannak olyan összetett funkciók, amelyeket egyszerűen lehetetlen verbálisan beállítani!” Igen, vannak ilyenek, de vannak olyan függvények, amelyeket egyszerűbb szóban leírni, mint képlettel beállítani. Például: "x minden természetes értéke a benne lévő számjegyek különbségének felel meg, míg a számbevitelben szereplő legnagyobb számjegyet vesszük a minuendnek." Most nézzük meg, hogyan valósul meg a gyakorlatban a funkció szóbeli leírása:

Egy adott szám legnagyobb számjegye - rendre - csökken, majd:

A funkciók fő típusai

Most térjünk át a legérdekesebbre - megvizsgáljuk azokat a fő függvénytípusokat, amelyekkel az iskolai és az intézeti matematika során dolgozott / dolgozott és fog dolgozni, vagyis megismerjük őket, úgymond, és Add nekik rövid leírás. Olvasson többet az egyes funkciókról a megfelelő részben.

Lineáris függvény

Az alak függvénye, ahol valós számok.

Ennek a függvénynek a grafikonja egy egyenes, tehát a konstrukció lineáris függvény két pont koordinátáinak megtalálására redukálódik.

Közvetlen pozíció bekapcsolva Koordináta sík a lejtéstényezőtől függ.

A függvény hatóköre (más néven argumentumtartomány) - .

Az értéktartomány a.

másodfokú függvény

Az űrlap függvénye, hol

A függvény grafikonja parabola, amikor a parabola ágai lefelé, amikor - felfelé irányulnak.

Sok ingatlan másodfokú függvény a diszkrimináns értékétől függ. A diszkriminánst a képlet számítja ki

A parabola helyzete a koordinátasíkon az értékhez és az együtthatóhoz képest az ábrán látható:

Tartomány

Az értékek tartománya az adott függvény szélsőértékétől (a parabola csúcsától) és az együtthatótól (a parabola ágainak irányától) függ.

Fordított arányosság

A képlet által adott függvény, ahol

A számot fordított arányossági tényezőnek nevezzük. Az értéktől függően a hiperbola ágai különböző négyzetekben vannak:

Tartomány - .

Az értéktartomány a.

ÖSSZEFOGLALÓ ÉS ALAPKÉPLET

1. A függvény egy olyan szabály, amely szerint a halmaz minden eleméhez hozzárendeljük a halmaz egyedi elemét.

• - ez egy függvényt jelölő képlet, vagyis az egyik változó függőségét a másiktól;
• - változó vagy argumentum;
• - függő érték - megváltozik, ha az argumentum megváltozik, vagyis egyesek szerint bizonyos képlet, amely egy mennyiségnek a másiktól való függőségét tükrözi.

2. Érvényes argumentumértékek, vagy egy függvény hatóköre az, ami összefügg azzal a lehetőséggel, amely alatt a függvénynek értelme van.

3. A függvényértékek tartománya- ez milyen értékeket igényel, érvényes értékekkel.

4. A funkció négyféleképpen állítható be:

• elemző (képletekkel);
• táblázatos;
• grafikus
• szóbeli leírás.

5. A függvények fő típusai:

• : , ahol valós számok;
• : , ahol;
• : , ahol.

Nemzeti Kutató Egyetem

Alkalmazott Földtani Tanszék

Absztrakt tovább felsőbb matematika

A témában: "Alapvető elemi funkciók,

tulajdonságaik és grafikonjaik"

Elkészült:

Ellenőrizve:

tanár

Meghatározás. Az y=a x képlettel adott függvényt (ahol a>0, a≠1) a bázisú exponenciális függvénynek nevezzük.

Fogalmazzuk meg az exponenciális függvény főbb tulajdonságait:

1. A definíciós tartomány az összes valós szám halmaza (R).

2. Az értéktartomány az összes pozitív valós szám halmaza (R+).

3. Ha a > 1, a függvény a teljes valós vonalon növekszik; 0-nál<а<1 функция убывает.

4. Általános funkció.

, az xО [-3;3] , az xО intervallumon [-3;3]

Az y(х)=х n alakú függvényt, ahol n az ОR szám, hatványfüggvénynek nevezzük. Az n szám különböző értéket vehet fel: egész és tört, páros és páratlan értéket egyaránt. Ettől függően a teljesítmény függvény más formát ölt. Tekintsünk olyan speciális eseteket, amelyek hatványfüggvények, és tükrözik az ilyen típusú görbék fő tulajdonságait a következő sorrendben: hatványfüggvény y \u003d x² (egy páros kitevővel rendelkező függvény - parabola), hatványfüggvény y \u003d x³ (függvény páratlan kitevővel - köbös parabolával) és y \u003d √ x (x ½ hatványig) függvénnyel (törtkitevővel rendelkező függvény), negatív egész kitevővel (hiperbola) rendelkező függvény.

Teljesítmény funkció y=x²

1. D(x)=R – a függvény a teljes numerikus tengelyen definiálva van;

2. E(y)= és növekszik az intervallumon

Teljesítmény funkció y=x³

1. Az y \u003d x³ függvény grafikonját köbös parabolának nevezzük. Az y=x³ hatványfüggvény a következő tulajdonságokkal rendelkezik:

2. D(x)=R – a függvény a teljes numerikus tengelyen definiálva van;

3. E(y)=(-∞;∞) – a függvény minden értéket felvesz a definíciós tartományában;

4. Ha x=0 y=0 – a függvény áthalad az O(0;0) origón.

5. A függvény a teljes definíciós tartományban növekszik.

6. A függvény páratlan (szimmetrikus az origóra).

, az xн intervallumon [-3;3]

Az x³ előtti numerikus tényezőtől függően a függvény lehet meredek / lapos és növelő / csökkenő.

Hatványfüggvény egész negatív kitevővel:

Ha az n kitevő páratlan, akkor egy ilyen hatványfüggvény grafikonját hiperbolának nevezzük. A negatív egész kitevővel rendelkező hatványfüggvény a következő tulajdonságokkal rendelkezik:

1. D(x)=(-∞;0)U(0;∞) bármely n esetén;

2. E(y)=(-∞;0)U(0;∞) ha n páratlan szám; E(y)=(0;∞) ha n páros szám;

3. A függvény a teljes definíciós tartományban csökken, ha n páratlan szám; a függvény a (-∞;0) intervallumon növekszik és a (0;∞) intervallumon csökken, ha n páros szám.

4. A függvény páratlan (szimmetrikus az origóra), ha n páratlan szám; egy függvény páros, ha n páros szám.

5. A függvény átmegy az (1;1) és (-1;-1) pontokon, ha n páratlan szám, valamint az (1;1) és (-1;1) pontokon, ha n páros szám.

, az xн intervallumon [-3;3]

Hatványfüggvény tört kitevővel

Az alak törtkitevőjű hatványfüggvény (kép) rendelkezik az ábrán látható függvény grafikonjával. A tört kitevővel rendelkező hatványfüggvény a következő tulajdonságokkal rendelkezik: (kép)

1. D(x) ОR, ha n páratlan szám és D(x)= , az xО intervallumon, az xО [-3;3] intervallumon

Az y \u003d log a x logaritmikus függvény a következő tulajdonságokkal rendelkezik:

1. D(x)н (0; + ∞) definíciós tartománya.

2. ÉrtéktartományE(y) О (- ∞; + ∞)

3. A függvény nem páros és nem páratlan (általános).

4. A függvény a (0; + ∞) intervallumon növekszik, ha a > 1, és csökken (0; + ∞) ha 0< а < 1.

Az y = log a x függvény grafikonját az y = a x függvény grafikonjából kaphatjuk meg az y = x egyenesre vonatkozó szimmetriatranszformáció segítségével. A 9. ábrán a > 1 logaritmikus függvény diagramja, a 10. ábrán pedig 0 esetén látható.< a < 1.

; az xн intervallumon; az xО intervallumon

Az y \u003d sin x, y \u003d cos x, y \u003d tg x, y \u003d ctg x függvényeket hívjuk. trigonometrikus függvények.

Az y \u003d sin x, y \u003d tg x, y \u003d ctg x függvények páratlanok, az y \u003d cos x függvények pedig párosak.

y függvény \u003d sin (x).

1. D(x) ОR definíciós terület.

2. Értéktartomány E(y) О [ - 1; egy].

3. A függvény periodikus; a főperiódus 2π.

4. A függvény páratlan.

5. A függvény növekszik a [ -π/2 + 2πn intervallumokon; π/2 + 2πn] és a [ π/2 + 2πn intervallumokon csökken; 3π/2 + 2πn], n О Z.

Az y \u003d sin (x) függvény grafikonja a 11. ábrán látható.