jelentése
Legnagyobb
jelentése
Legkevésbé
maximális pont
Mélypont
A függvény szélsőpontjainak megtalálásának feladatait a standard séma szerint oldjuk meg 3 lépésben.
1. lépés. Keresse meg egy függvény deriváltját
- Jegyezze meg a származékos képleteket elemi függvények valamint a differenciálás alapvető szabályai a származék megtalálásához.
y′(x)=(x3−243x+19)′=3x2−243.
2. lépés. Keresse meg a derivált nulláit!
- Oldja meg a kapott egyenletet, és keresse meg a derivált nulláit!
3x2−243=0⇔x2=81⇔x1=−9,x2=9.
3. lépés. Keress szélsőséges pontokat
- Használja a térköz módszert a derivált előjeleinek meghatározásához;
- A minimumponton a derivált nulla, és az előjelet mínuszról pluszra, a maximum pontnál pedig pluszról mínuszra változtatja.
Alkalmazzuk ezt a megközelítést a következő probléma megoldására:
Határozzuk meg az y=x3−243x+19 függvény maximális pontját.
1) Keresse meg a deriváltot: y′(x)=(x3−243x+19)′=3x2−243;
2) Oldja meg az y′(x)=0 egyenletet: 3x2−243=0⇔x2=81⇔x1=−9,x2=9;
3) A derivált pozitív x>9 és x esetén<−9 и отрицательная при −9 Hogyan találjuk meg egy függvény legnagyobb és legkisebb értékét A függvény legnagyobb és legkisebb értékének megtalálásának problémájának megoldása szükséges: Sok feladatban segít tétel: Ha csak egy szélsőpont van a szakaszon, és ez a minimumpont, akkor abban érjük el a függvény legkisebb értékét. Ha ez a maximális pont, akkor a maximális értéket érte el. 14. A határozatlan integrál fogalma és alapvető tulajdonságai. Ha a funkció f(x x, és k- akkor szám Röviden szólva: a konstans kivehető az integráljelből. Ha funkciókat f(x) és g(x) van antiderivatív az intervallumon x, akkor Röviden szólva: az összeg integrálja egyenlő az integrálok összegével. Ha a funkció f(x) van egy antiderivált az intervallumon x, akkor ennek az intervallumnak a belső pontjaira: Röviden szólva: az integrál deriváltja egyenlő az integrandusszal. Ha a funkció f(x) folyamatos az intervallumon xés ennek az intervallumnak a belső pontjain differenciálható, akkor: Röviden szólva: egy függvény differenciáljának integrálja egyenlő azzal a függvénnyel plusz az integrációs állandóval. Adjunk meg egy szigorú matematikai definíciót határozatlan integrál fogalmai. A kedves kifejezés az ún a függvény integrálja f(x)
, ahol f(x)
- integrand függvény, amely adott (ismert), dx
- differenciálmű x
, mindig jelen lévő szimbólummal dx
. Meghatározás. Határozatlan integrál függvénynek nevezzük F(x) + C
, amely tetszőleges állandót tartalmaz C
, amelynek differenciája egyenlő integrand kifejezés f(x)dx
, azaz Emlékezzen arra - funkció differenciálés a következőképpen van meghatározva: Probléma keresése határozatlan integrál funkciót találni derivált amely egyenlő az integrandusszal. Ez a függvény egy állandóig van meghatározva, mert az állandó deriváltja nulla. Például ismert, hogy , akkor kiderül, hogy Feladat keresése határozatlan integrál A függvényekből nem olyan egyszerű és könnyű, mint amilyennek első pillantásra tűnik. Sok esetben szakértelemmel kell dolgozni határozatlan integrálok, olyan élménynek kell lennie, amely gyakorlással jár és állandó példák megoldása határozatlan integrálokra.Érdemes megfontolni azt a tényt, hogy határozatlan integrálok egyes függvényekből (elég sok van belőlük) nem veszik át az elemi függvényekben. 15. Alapvető határozatlan integrálok táblázata. Alapképletek 16. Határozott integrál, mint az integrálösszeg határa. Az integrál geometriai és fizikai jelentése. Legyen az y=ƒ(x) függvény az [a; Zenekar< b. Выполним следующие действия. 1. Az x 0 \u003d a, x 1, x 2, ..., x n \u003d B (x 0) pontok felhasználásával 2. Minden i = 1,2,...,n részszakaszban kiválasztunk egy tetszőleges pontot i є-vel, és kiszámoljuk a függvény értékét, azaz az ƒ(i-vel) értéket. 3. Szorozzuk meg az ƒ függvény talált értékét (i-ből) a megfelelő részszakasz ∆x i =x i -x i-1 hosszával: ƒ (i-ből) ∆х i. 4. Állítsa össze az összes ilyen szorzat S n összegét: A (35.1) alak összegét az y \u003d ƒ (x) függvény integrál összegének nevezzük az [a; b]. Jelölje λ-val a legnagyobb részszakasz hosszát: λ = max ∆x i (i = 1,2,..., n). 5. Határozzuk meg a (35.1) integrálösszeg határát n → ∞ úgy, hogy λ→0! Ha ezen felül az S n integrálösszegnek van egy I határértéke, amely nem függ a szegmens felosztásának módjától [a; b] parciális szegmensekbe, vagy az azokban lévő pontok megválasztásából, akkor az I számot az y = ƒ(x) függvény határozott integráljának nevezzük az [a; b] és így jelöljük, Az a és b számokat rendre az integráció alsó és felső határának nevezzük, ƒ(x) - integrandus, ƒ(x) dx - integrandus, x - integrációs változó, szegmens [a; b] - integrációs terület (szegmens). Az y \u003d ƒ (x) függvény, amelyre az [a; b] ezen az intervallumon van egy integrálható integrál. Fogalmazzuk meg most a létezési tételt egy határozott integrálra. 35.1. tétel (Cauchy). Ha az y = ƒ(x) függvény folytonos az [a; b], akkor a határozott integrál Vegyük észre, hogy egy függvény folytonossága elégséges feltétele az integrálhatóságának. Egy meghatározott integrál azonban létezhet bizonyos nem folytonos függvényekre is, különösen minden olyan függvényre, amely egy intervallumra korlátos, és véges számú szakadási ponttal rendelkezik. Mutassunk rá a határozott integrál néhány olyan tulajdonságára, amelyek közvetlenül a (35.2) definíciójából következnek. 1. A határozott integrál független az integrációs változó jelölésétől: Ez abból adódik, hogy az integrálösszeg (35.1) és ennek következtében a határértéke (35.2) nem függ attól, hogy melyik betű jelöli ennek a függvénynek az argumentumát. 2. Egy határozott integrál azonos integrációs határokkal egyenlő nullával: 3. Bármely valós számra c. 17. Newton-Leibniz képlet. Határozott integrál alapvető tulajdonságai. Legyen a függvény y = f(x) folyamatos a szegmensen
és F(x) akkor a függvény egyik antideriváltja ezen a szegmensen Newton-Leibniz képlet: A Newton-Leibniz képlet ún az integrálszámítás alapképlete. A Newton-Leibniz formula bizonyításához szükségünk van egy változó felső határú integrál fogalmára. Ha a funkció y = f(x) folyamatos a szegmensen
, akkor az argumentum formájának integrálja a felső határ függvénye. Ezt a függvényt jelöljük Valóban, írjuk fel az argumentum növekményének megfelelő függvény növekményét, és használjuk a határozott integrál ötödik tulajdonságát és a tizedik tulajdonságból származó következményt: Írjuk át ezt az egyenlőséget a formába Kiszámít F(a), a határozott integrál első tulajdonságát használva: Egy függvény növekményét általában úgy jelöljük A Newton-Leibniz képlet alkalmazásához elég, ha ismerjük az egyik antiderivált y=F(x) integrand y=f(x) a szegmensen
és számítsa ki ennek az antiderivatívának a növekményét ezen a szegmensen. A cikkben az integrációs módszereket elemzik az antiderivatív megtalálásának fő módjai. Adjunk néhány példát határozott integrálok kiszámítására a Newton-Leibniz képlet segítségével a pontosítás érdekében. Példa. Számítsa ki a határozott integrál értékét a Newton-Leibniz képlet segítségével! Megoldás. Először is vegye figyelembe, hogy az integrandus folytonos az intervallumon
, tehát integrálható rajta. (Az integrálható függvényekről az olyan függvények részben beszéltünk, amelyekre van határozott integrál). A határozatlan integrálok táblázatából látható, hogy egy függvény esetében az argumentum (és így a for ) valós értékére vonatkozó antideriválták halmaza így van írva. Vegyük a primitívet C=0: . Most már csak a Newton-Leibniz képletet kell használni a határozott integrál kiszámításához: 18. Határozott integrál geometriai alkalmazásai. EGY HATÁROZOTT INTEGRÁL GEOMETRIAI ALKALMAZÁSAI Testtérfogat számítás A testtérfogat kiszámítása párhuzamos szakaszok ismert területeiből: A forgótest térfogata: ; . 1. példa. Keresse meg egy alakzat területét, amelyet egy görbe y=sinx, egyenesek határolnak Megoldás: Az ábra területének megkeresése: 2. példa. Számítsa ki egy vonallal határolt ábra területét! Megoldás: Határozzuk meg ezen függvények grafikonjainak metszéspontjainak abszcisszáját! Ehhez megoldjuk az egyenletrendszert Innen találjuk x 1 \u003d 0, x 2 = 2,5. 19. A differenciálvezérlés fogalma. Elsőrendű differenciálegyenletek. Differenciálegyenlet- egy egyenlet, amely összekapcsolja egy függvény deriváltjának értékét magával a függvénnyel, a független változó értékeivel, számokkal (paraméterekkel). Az egyenletben szereplő deriváltak sorrendje eltérő lehet (formálisan semmi sem korlátozza). A deriváltok, függvények, független változók és paraméterek különféle kombinációkban szerepelhetnek az egyenletben, vagy legalább egy derivált kivételével az összes származéka hiányozhat. Nem olyan egyenlet, amely egy ismeretlen függvény deriváltjait tartalmazza, differenciálegyenlet. Például, Parciális differenciálegyenletek(URCHP) olyan egyenletek, amelyek több változó ismeretlen függvényeit és parciális deriváltjaikat tartalmazzák. Az ilyen egyenletek általános formája a következőképpen ábrázolható: ahol független változók, és ezeknek a változóknak a függvénye. A parciális differenciálegyenletek sorrendje ugyanúgy meghatározható, mint a közönséges differenciálegyenletek esetében. A parciális differenciálegyenletek másik fontos osztályozása az elliptikus, parabolikus és hiperbolikus típusú egyenletekre való felosztásuk, különösen a másodrendű egyenletek esetében. A közönséges differenciálegyenletek és a parciális differenciálegyenletek egyaránt feloszthatók lineárisés nem lineáris. Egy differenciálegyenlet akkor lineáris, ha az ismeretlen függvény és deriváltjai csak az első hatványig lépnek be az egyenletbe (és nem szoroznak egymással). Az ilyen egyenleteknél a megoldások a függvények terének affin alterét alkotják. A lineáris differenciálegyenletek elmélete sokkal mélyebben fejlődött, mint a nemlineáris egyenletek elmélete. Lineáris differenciálegyenlet általános alakja n- sorrend: ahol pi(x) a független változó ismert függvényei, amelyeket az egyenlet együtthatóinak nevezünk. Funkció r(x) a jobb oldalon az úgynevezett ingyenes tag(az egyetlen kifejezés, amely nem függ az ismeretlen függvénytől) A lineáris egyenletek egy fontos osztálya a lineáris differenciálegyenletek állandó együtthatók. A lineáris egyenletek egy alosztálya az homogén differenciálegyenletek - szabad kifejezést nem tartalmazó egyenletek: r(x) = 0. Homogén differenciálegyenletekre érvényes a szuperpozíció elve: egy ilyen egyenlet adott megoldásainak lineáris kombinációja is a megoldás lesz. Az összes többi lineáris differenciálegyenletet ún heterogén differenciál egyenletek. A nemlineáris differenciálegyenletek általános esetben nem rendelkeznek kidolgozott megoldási módszerekkel, kivéve néhány speciális osztályt. Bizonyos esetekben (bizonyos közelítések alkalmazásával) lineárisra redukálhatók. Például egy harmonikus oszcillátor lineáris egyenlete · egy másodrendű homogén differenciálegyenlet állandó együtthatókkal. A megoldás egy függvénycsalád , ahol és tetszőleges állandók, amelyek egy adott megoldáshoz külön meghatározott kezdeti feltételekből kerülnek meghatározásra. Ez az egyenlet különösen egy 3-as ciklikus frekvenciájú harmonikus oszcillátor mozgását írja le. · Newton második törvénye felírható differenciálegyenlet formájában · A Bessel-differenciálegyenlet egy közönséges lineáris, másodrendű homogén egyenlet változó együtthatókkal: Megoldásai a Bessel-függvények. Példa egy nem-homogén, nem lineáris, 1. rendű közönséges differenciálegyenletre: A következő példacsoportban az ismeretlen függvény u két változótól függ xés t vagy xés y. Elsőrendű homogén lineáris parciális differenciálegyenlet: Egydimenziós hullámegyenlet - homogén lineáris egyenlet a másodrendű hiperbolikus típusú parciális deriváltokban állandó együtthatókkal, leírja a húr rezgését, ha - a húr eltérését egy koordinátájú pontban x akkor t, és a paraméter a beállítja a karakterlánc tulajdonságait: A Laplace-egyenlet a kétdimenziós térben egy homogén lineáris differenciálegyenlet másodrendű elliptikus típusú parciális deriváltokban állandó együtthatókkal, amely számos mechanikai, hővezetési, elektrosztatikai, hidraulika fizikai problémában felmerül: A Korteweg-de Vries egyenlet, egy nemlineáris harmadrendű parciális differenciálegyenlet, amely stacionárius nemlineáris hullámokat ír le, beleértve a szolitonokat is: 20. Differenciálegyenletek elválasztható alkalmazható. Lineáris egyenletek és a Bernoulli-módszer. Az elsőrendű lineáris differenciálegyenlet olyan egyenlet, amely egy ismeretlen függvényhez és annak deriváltjához képest lineáris. Egész fokozatú formája van. Valóban, ha megtaláljuk és behelyettesítjük a vizsgált típusok egyenleteit, akkor a helyes egyenlőséget kapjuk. Amint az a cikkben olvasható homogén egyenletek, ha feltétel szerint csak egy adott megoldást kell találni, akkor a függvény érthető okokból nem zavar bennünket, de ha általános megoldást / integrált kell találni, akkor gondoskodni kell arról, hogy ez a függvény nem veszett el! Elhoztam a Bernoulli-egyenlet összes népszerű változatát egy nagy zsákban ajándékokkal, és folytattam a terjesztést. Akaszd fel a zoknidat a fa alá. 1. példa Keresse meg a differenciálegyenletnek az adott kezdeti feltételnek megfelelő megoldását! Valószínűleg sokan meglepődtek azon, hogy az első ajándékot is azonnal kivették a táskából Cauchy probléma. Ez nem véletlen. Amikor Bernoulli-egyenletet javasolnak egy megoldásra, valamilyen oknál fogva gyakran meg kell találni egy adott megoldást. Gyűjteményemben 10 Bernoulli-egyenletből álló véletlenszerű mintát készítettem, és az általános megoldást (konkrét megoldás nélkül) mindössze 2 egyenletben kell megtalálni. De valójában ez apróság, hiszen az általános megoldást mindenképpen keresni kell. Megoldás: Ez a diffur alakja , és ezért a Bernoulli-egyenlet A függvény legnagyobb értéke A függvény legkisebb értéke Ahogy a keresztapa mondta: "Semmi személyes." Csak származékok! A statisztika 12. feladatát meglehetősen nehéznek tartják, és mindez azért, mert a srácok nem olvasták el ezt a cikket (vicc). A legtöbb esetben a figyelmetlenség a hibás. 12 feladat kétféle: Feladatok a vizsgával: Keresse meg a függvény maximális pontját Keresse meg a függvény minimális pontját Feladatok a vizsgával: Keresse meg a függvény legnagyobb értékét a [−4; −1] Válasz: -6 Keresse meg a függvény legnagyobb értékét a szakaszon Válasz: 11 Következtetések: A függvény szélsőpontja az a pont a függvény tartományában, ahol a függvény értéke minimum vagy maximum értéket vesz fel. Az ezeken a pontokon lévő függvényértékeket a függvény szélsőértékeinek (minimum és maximum) nevezzük. Meghatározás. Pont x1
funkció hatóköre f(x) nak, nek hívják a függvény maximális pontja
, ha a függvény értéke ezen a ponton nagyobb, mint a függvény értékei a hozzá kellően közeli pontokban, amelyek tőle jobbra és balra helyezkednek el (azaz az egyenlőtlenség f(x0
) > f(x 0
+ Δ x)
x1
maximális. Meghatározás. Pont x2
funkció hatóköre f(x) nak, nek hívják a függvény minimális pontja, ha a függvény értéke ezen a ponton kisebb, mint a függvény értékei a hozzá kellően közeli pontokban, amelyek tőle jobbra és balra helyezkednek el (azaz az egyenlőtlenség f(x0
) < f(x 0
+ Δ x)
). Ebben az esetben azt mondjuk, hogy a függvény a pontban van x2
minimális. Mondjuk a lényeget x1
- a függvény maximális pontja f(x) . Majd az intervallumban ig x1
funkciója növekszik, tehát a függvény deriváltja nagyobb nullánál ( f "(x) > 0 ), és az azt követő intervallumban x1
a függvény csökken, tehát függvény deriváltja nullánál kisebb ( f "(x) < 0
).
Тогда в точке x1
Tegyük fel azt is, hogy a lényeg x2
- a függvény minimális pontja f(x) . Majd az intervallumban ig x2
a függvény csökkenőben van, és a függvény deriváltja kisebb, mint nulla ( f "(x) < 0
), а в интервале
после x2
a függvény növekszik, és a függvény deriváltja nagyobb, mint nulla ( f "(x) > 0). Ebben az esetben is a ponton x2
a függvény deriváltja nulla vagy nem létezik. Fermat tétel ( szükséges funkció a függvény szélsőértékének megléte). Ha pont x0
- a függvény szélsőpontja f(x), akkor ezen a ponton a függvény deriváltja egyenlő nullával ( f "(x) = 0 ) vagy nem létezik. Meghatározás. Meghívjuk azokat a pontokat, ahol egy függvény deriváltja egyenlő nullával, vagy nem létezik kritikus pontok
. 1. példa Tekintsünk egy függvényt. Azon a ponton x= 0 a függvény deriváltja egyenlő nullával, ezért a pont x= 0 a kritikus pont. A függvény grafikonján azonban látható, hogy a teljes definíciós tartományban növekszik, tehát a pont x= 0 ennek a függvénynek nem szélsőpontja. Tehát azok a feltételek, hogy egy függvény deriváltja egy pontban egyenlő nullával, vagy nem létezik, szükséges feltételek egy szélsőséghez, de nem elégségesek, hiszen más példákat is lehet adni olyan függvényekre, amelyekre ezek a feltételek teljesülnek, de a függvény nincs extrémuma a megfelelő pontban. Ezért elegendő jelzéssel kell rendelkeznie, amelyek lehetővé teszik annak megítélését, hogy egy adott kritikus ponton van-e szélsőség, és melyik - maximum vagy minimum. Tétel (az első elégséges kritérium egy függvény szélsőértékének létezéséhez). Kritikus pont x0
f(x) , ha a függvény deriváltja ezen a ponton áthaladva előjelet vált, és ha az előjel "plusz"-ról "mínuszra" változik, akkor a maximum pont, ha pedig "mínusz"-ról "plusz", akkor a minimum pont . Ha a pont közelében x0
, tőle balra és jobbra a derivált megtartja előjelét, ez azt jelenti, hogy a függvény vagy csak csökken, vagy csak a pont valamely környezetében nő. x0
. Ebben az esetben a ponton x0
nincs extrémum. Így, a függvény szélsőpontjainak meghatározásához a következőket kell tennie
: 2. példa Keresse meg egy függvény szélsőértékét Megoldás. Keressük meg a függvény deriváltját: Egyenlítse a derivált nullával a kritikus pontok meghatározásához: Mivel az "x" bármely értékénél a nevező nem egyenlő nullával, a számlálót nullával egyenlővé tesszük: Van egy kritikus pont x= 3. Meghatározzuk a derivált előjelét az e pont által határolt intervallumokban: a mínusz végtelentől a 3-ig terjedő tartományban - mínusz jel, azaz a függvény csökken, a 3-tól a plusz végtelenig terjedő tartományban - pluszjel, vagyis a függvény növekszik. Vagyis pont x= 3 a minimumpont. Keresse meg a függvény értékét a minimumpontban: Így a függvény szélsőpontja: (3; 0) , és ez a minimumpont. Tétel (a függvény szélsőértékének létezésének második elégséges kritériuma). Kritikus pont x0
a függvény szélsőpontja f(x), ha a függvény második deriváltja ezen a ponton nem egyenlő nullával ( f ""(x) ≠ 0 ), sőt, ha a második derivált nagyobb, mint nulla ( f ""(x) > 0 ), akkor a maximális pont, és ha a második derivált kisebb, mint nulla ( f ""(x) < 0
),
то точкой минимума. Megjegyzés 1. Ha egy ponton x0
az első és a második származék is eltűnik, akkor ezen a ponton nem lehet a második elégséges jel alapján megítélni a szélsőség jelenlétét. Ebben az esetben az első elégséges kritériumot kell használnia a függvény szélsőértékéhez. 2. megjegyzés. A függvény szélsőértékére vonatkozó második elégséges kritérium szintén nem alkalmazható, ha az első derivált nem létezik a stacionárius pontban (akkor a második derivált sem létezik). Ebben az esetben is szükséges az első elégséges kritériumot használni a függvény szélsőértékéhez. A fenti definíciókból következik, hogy egy függvény szélsőértéke lokális jellegű - ez a függvény legnagyobb és legkisebb értéke a legközelebbi értékekhez képest. Tegyük fel, hogy a bevételeit egy éves időtartamra tekinti. Ha májusban 45 000 rubelt, áprilisban 42 000 rubelt, júniusban 39 000 rubelt keresett, akkor a májusi bevétel a bevételi függvény maximuma a legközelebbi értékekhez képest. Októberben azonban 71 000 rubelt, szeptemberben 75 000 rubelt, novemberben 74 000 rubelt keresett, tehát az októberi bevétel a kereseti függvény minimuma a közeli értékekhez képest. És könnyen belátható, hogy az április-május-június értékek között a maximum kevesebb, mint a szeptember-október-november minimum. Általánosságban elmondható, hogy egy függvénynek több szélsőértéke is lehet egy intervallumon, és kiderülhet, hogy a függvény bármely minimuma nagyobb, mint bármely maximum. Tehát a fenti ábrán látható függvényhez . Vagyis nem szabad azt gondolni, hogy a függvény maximuma és minimuma a maximális és minimális értéke a teljes vizsgált szegmensben. A maximum ponton a függvénynek csak azokhoz az értékekhez viszonyítva van a legnagyobb értéke, amelyek minden pontján kellően közel vannak a maximális ponthoz, a minimum ponton pedig csak azokhoz az értékekhez képest a legkisebb értéke. hogy minden pontján kellően közel van a minimumponthoz. Ezért finomíthatjuk a függvény szélsőpontjainak fenti fogalmát, és a minimumpontokat helyi minimumpontoknak, a maximumpontokat pedig helyi maximumpontoknak nevezhetjük. 3. példa Megoldás: A függvény definiált és folytonos az egész számegyenesen. A származéka Az intervallumra vonatkoztatási pont lehet: találjuk. Ha egy pontot veszünk az intervallumban, azt kapjuk, hogy az intervallumban egy pontot veszünk, akkor . Tehát az intervallumokban és , és az intervallumban. Az első szerint elégséges jel szélsőség, a pontban nincs szélsőérték (mivel a derivált az intervallumban megtartja előjelét), és a pontban a függvénynek van minimuma (mivel a derivált előjelet változtat mínuszról pluszra, amikor ezen a ponton halad át). Keresse meg a függvény megfelelő értékeit: , és . Az intervallumban a függvény csökken, mivel ebben az intervallumban , az intervallumban pedig nő, mivel ebben az intervallumban. A gráf felépítésének tisztázása érdekében keressük meg annak metszéspontjait a koordinátatengelyekkel. Ha olyan egyenletet kapunk, amelynek gyöke és , azaz a függvény grafikonjának két pontja (0; 0) és (4; 0) található. Az összes kapott információ felhasználásával grafikont készítünk (lásd a példa elején). A számítások során végzett önellenőrzéshez használhatja online származékos kalkulátor . 4. példa Keresse meg a függvény szélsőértékét, és készítse el a grafikonját. A függvény tartománya a teljes számegyenes, kivéve a pontot, azaz. . A vizsgálat lerövidítésére felhasználhatjuk azt a tényt, hogy ez a függvény páros, hiszen A származék megkeresése 1) 2) de a függvény ezen a ponton törést szenved, így nem lehet szélsőpont. Ily módon adott funkciót két kritikus pontja van: és . Figyelembe véve a függvény paritását, csak a pontot ellenőrizzük a szélsőérték második elégséges jelével. Ehhez megtaláljuk a második deriváltot Ahhoz, hogy teljesebb képet kapjunk a függvény grafikonjáról, nézzük meg annak viselkedését a definíciós tartomány határain: (itt a szimbólum a vágyat jelzi x nullára a jobb oldalon, és x pozitív marad; hasonlóképpen törekvést jelent x nullára a bal oldalon, és x negatív marad). Így ha , akkor . Ezután megtaláljuk azok. ha akkor . A függvény grafikonjának nincs metszéspontja a tengelyekkel. A kép a példa elején található. A számítások során végzett önellenőrzéshez használhatja online származékos kalkulátor . 8. példa Keresse meg a függvény szélsőértékét. Megoldás. Keresse meg a függvény tartományát. Mivel az egyenlőtlenségnek fennállnia kell, ebből kapjuk. Keressük meg a függvény első deriváltját. Tétel.
(az extrémum meglétének szükséges feltétele) Ha az f (x) függvény differenciálható az x \u003d x 1 pontban, és az x 1 pont szélsőpont, akkor a függvény deriváltja ezen a ponton eltűnik. Bizonyíték.
Tegyük fel, hogy az f(x) függvény maximuma az x = x 1 pontban van. Ekkor kellően kis pozitív Dх>0 esetén a következő egyenlőtlenség igaz: Definíció szerint: Azok. ha Dх®0, de Dх<0, то f¢(x 1) ³ 0, а если Dх®0, но Dх>0, majd f¢(x 1) 0 GBP. És ez csak akkor lehetséges, ha Dх®0-nél f¢(x 1) = 0. Abban az esetben, ha az f(x) függvénynek minimuma van az x 2 pontban, a tételt hasonlóan bizonyítjuk. A tétel bizonyítást nyert. Következmény.
Ennek a fordítottja nem igaz. Ha egy függvény deriváltja egy ponton nulla, akkor ez nem jelenti azt, hogy a függvénynek ezen a ponton van szélsősége. Beszédes példa erre az y \u003d x 3 függvény, amelynek deriváltja az x \u003d 0 pontban egyenlő nullával, de ezen a ponton a függvénynek csak inflexiója van, maximuma vagy minimuma nem. Meghatározás. kritikus pontok A függvények olyan pontok, ahol a függvény deriváltja nem létezik, vagy egyenlő nullával. A fent vizsgált tétel megadja a szükséges feltételeket a szélsőség létezéséhez, de ez nem elég. Példa: f(x) = ôxô Példa: f(x) = Az x = 0 pontban a függvénynek van minimuma, de az x = 0 pontban egyik sem nincs származéka. maximum, nincs minimum, nem Általánosságban elmondható, hogy az f(x) függvénynek lehet szélsősége azokban a pontokban, ahol a derivált nem létezik, vagy egyenlő nullával. Tétel.
(Elegendő feltételek szélsőség megléte) Legyen az f(x) függvény folytonos abban az (a, b) intervallumban, amely az x 1 kritikus pontot tartalmazza, és ennek az intervallumnak minden pontjában differenciálható (kivéve talán magát az x 1 pontot). Ha az x 1 ponton balról jobbra haladva az f¢(x) függvény deriváltja „+”-ról „-”-re változtatja az előjelet, akkor az x = x 1 pontban az f(x) függvény egy maximum, és ha a derivált előjelet „-”-ről „+”-ra változtat, akkor a függvénynek van minimuma. Bizonyíték.
Hadd Lagrange tétele szerint: f(x) - f(x 1) = f¢(e)(x - x 1), ahol x< e < x 1 . Ekkor: 1) Ha x< x 1 , то e < x 1 ; f¢(e)>0; f¢(e)(x – x 1)<0, следовательно f(x) – f(x 1)<0 или f(x) < f(x 1). 2) Ha x > x 1, akkor e > x 1 f¢(e)<0; f¢(e)(x – x 1)<0, следовательно f(x) – f(x 1)<0 или f(x) < f(x 1). Mivel a válaszok ugyanazok, azt mondhatjuk, hogy f(x)< f(x 1) в любых точках вблизи х 1 , т.е. х 1 – точка максимума. A minimumpontra vonatkozó tétel bizonyítása hasonló módon történik. A tétel bizonyítást nyert. A fentiek alapján egyetlen eljárást lehet kidolgozni a legnagyobb és a legkisebb érték funkciók a szegmensen: 1) Keresse meg a függvény kritikus pontjait! 2) Keresse meg a függvény értékeit a kritikus pontokban. 3) Keresse meg a függvény értékeit a szegmens végén. 4) Válassza ki a kapott értékek közül a legnagyobbat és a legkisebbet. Függvény vizsgálata szélsőségig segítségével magasabb rendű származékai. Legyen f¢(x 1) = 0 az x = x 1 pontban, és legyen f¢¢(x 1) és legyen folytonos az x 1 pont valamely környezetében. Tétel.
Ha f¢(x 1) = 0, akkor az f(x) függvénynek az x = x 1 pontban van maximuma, ha f¢¢(x 1)<0 и минимум, если f¢¢(x 1)>0.
Bizonyíték.
Legyen f¢(x 1) = 0 és f¢¢(x 1)<0. Т.к. функция f(x) непрерывна, то f¢¢(x 1) будет отрицательной и в некоторой малой окрестности точки х 1 . Mert f¢¢(x) = (f¢(x))¢< 0, то f¢(x) убывает на отрезке, содержащем точку х 1 , но f¢(x 1)=0, т.е. f¢(x) >0 x-nél Függvényminimum esetén a tételt hasonlóan bizonyítjuk. Ha f¢¢(x) = 0, akkor a kritikus pont természete ismeretlen. Ennek megállapításához további kutatások szükségesek. A görbe domborúsága és homorúsága. Inflexiós pontok. Meghatározás.
A görbe domború fel az (a, b) intervallumon, ha minden pontja az ezen az intervallumon lévő bármely érintője alatt van. A felfelé konvex pontú görbét nevezzük konvex, és a lefelé konvex görbét ún homorú. Az ábra a fenti definíciót szemlélteti. 1. tétel.
Ha az (a, b) intervallum minden pontjában az f(x) függvény második deriváltja negatív, akkor az y = f(x) görbe felfelé konvex (konvex). Bizonyíték.
Legyen x 0 О (a, b). Rajzolja meg a görbe érintőjét ezen a ponton. Görbeegyenlet: y = f(x); Érintőegyenlet: Ezt bizonyítani kell. A Lagrange-tétel alapján f(x) – f(x 0) esetén: , x 0< c < x. A Lagrange-tétel szerint Legyen x > x 0, majd x 0< c 1 < c < x. Т.к. x – x 0 >0 és c - x 0 > 0, valamint feltétel szerint Következésképpen,. Legyen x< x 0 тогда x < c < c 1 < x 0 и x – x 0 < 0, c – x 0 < 0, т.к. по условию то Hasonlóan igazolható, hogy ha f¢¢(x) > 0 az (a, b) intervallumon, akkor az y=f(x) görbe konkáv az (a, b) intervallumon. A tétel bizonyítást nyert. Meghatározás.
A görbe konvex részét a konkáv résztől elválasztó pontot ún inflexiós pont. Nyilvánvaló, hogy az inflexiós pontban az érintő metszi a görbét. 2. tétel.
Legyen a görbe az y = f(x) egyenlettel definiálva. Ha a második derivált f¢¢(a) = 0 vagy f¢¢(a) nem létezik, és az x = a f¢¢(x) ponton áthaladva előjelet vált, akkor a görbe x abszcissza pontja = a egy inflexiós pont. Bizonyíték.
1) Legyen f¢¢(x)< 0 при х < a и f¢¢(x) >0 x > a esetén. Aztán at x< a кривая выпукла, а при x >egy görbe homorú, azaz. az x = a pont az inflexiós pont. 2) Legyen f¢¢(x) > 0 x-re< b и f¢¢(x) < 0 при x < b. Тогда при x < b кривая обращена выпуклостью вниз, а при x >b - kidudorodik. Ekkor x = b egy inflexiós pont. A tétel bizonyítást nyert. Aszimptoták. A függvények tanulmányozása során gyakran előfordul, hogy ha egy görbe egy pontjának x-koordinátáját a végtelenbe eltávolítjuk, a görbe korlátlanul közelít egy bizonyos egyeneshez. Meghatározás.
Közvetlen hívás aszimptota görbe, ha a görbe változó pontja és az egyenes közötti távolság nullára hajlik, amikor a pontot a végtelenbe eltávolítjuk. Meg kell jegyezni, hogy nem minden görbének van aszimptotája. Az aszimptoták lehetnek egyenesek vagy ferdék. Az aszimptoták jelenlétére vonatkozó függvények tanulmányozása megvan nagyon fontosés lehetővé teszi a függvény jellegének és a görbe grafikonjának viselkedésének pontosabb meghatározását. Általánosságban elmondható, hogy a görbe korlátlanul közeledve az aszimptotájához, metszheti is, és nem egy pontban, ahogy az alábbi függvény grafikonján látható. Tekintsük részletesebben a görbék aszimptotáinak megtalálásának módszereit. Függőleges aszimptoták. Az aszimptota definíciójából következik, hogy ha vagy vagy , akkor az x = a egyenes az y = f(x) görbe aszimptotája. Például egy függvény esetében az x = 5 egyenes a függőleges aszimptota. Ferde aszimptoták. Tegyük fel, hogy az y = f(x) görbének van egy y = kx + b ferde aszimptotája. Jelöljük ki a görbe és az aszimptotra merőleges metszéspontját - M, P - ennek a merőlegesnek az aszimptotával való metszéspontját. Az aszimptota és az x tengely közötti szöget j jelöli. Az x tengelyre merőleges MQ metszi az aszimptotát az N pontban. Ekkor MQ = y a görbe pontjának ordinátája, NQ = az N pont ordinátája az aszimptoton. Feltétel szerint: , РNMP = j, . A j szög állandó és nem egyenlő 90 0 , akkor Akkor Tehát az y = kx + b egyenes a görbe aszimptotája. Mert pontos meghatározás Ezen a vonalon meg kell találni a módját a k és b együtthatók kiszámításának. Az eredményül kapott kifejezésben kivesszük x-et a zárójelekből: Mert x®¥, akkor Akkor Mert Vegye figyelembe, hogy a vízszintes aszimptoták a ferde aszimptoták speciális esetei k = 0 esetén. Példa. 1) Függőleges aszimptoták: y®+¥ x®0-0: y®-¥ x®0+0, ezért az x = 0 függőleges aszimptota. 2) Ferde aszimptoták: Így az y = x + 2 egyenes egy ferde aszimptota. Ábrázoljuk a függvényt: Példa. Keressen aszimptotákat, és ábrázolja a függvényt. Az x=3 és x=-3 vonalak a görbe függőleges aszimptotái. Keresse meg a ferde aszimptotákat: y = 0 a vízszintes aszimptota. Példa. Keressen aszimptotákat és ábrázolja a függvényt Az x = -2 egyenes a görbe függőleges aszimptotája. Keressünk ferde aszimptotákat. Összességében az y = x - 4 egyenes egy ferde aszimptota. Funkciótanulmányi séma Egy függvény kutatásának folyamata több szakaszból áll. A függvény viselkedésének és grafikonjának természetének legteljesebb elképzeléséhez meg kell találni: 1) A funkció hatóköre. Ez a fogalom magában foglalja mind az értékek tartományát, mind a funkció hatókörét. 2) Töréspontok. (Ha rendelkezésre állnak). 3) Növekedési és csökkenési intervallumok. 4) Maximum és minimum pontok. 5) Maximum és minimális érték a tartományában működik. 6) Konvexitás és homorú területek. 7) Inflexiós pontok (ha vannak). 8) Aszimptoták (ha vannak). 9) Grafikon készítése. Használjuk ezt a sémát egy példával. Példa. Vizsgáljunk meg egy függvényt, és ábrázoljuk a grafikonját. Megtaláljuk a függvény létezési területét. Ez nyilvánvaló definíciós tartomány függvény a terület (-¥; -1) È (-1; 1) È (1; ¥). Az viszont látható, hogy az x = 1, x = -1 egyenesek függőleges aszimptoták görbe. Értékterület ennek a függvénynek az intervallum (-¥; ¥). töréspontok függvények az x=1, x=-1 pontok. Találunk kritikus pontok. Keressük meg a függvény deriváltját Kritikus pontok: x = 0; x = - ; x = ; x=-1; x = 1. Keressük meg a függvény második deriváltját Határozzuk meg a görbe domborúságát és konkávságát az intervallumokban. -¥ < x < - , y¢¢ < 0, кривая выпуклая - < x < -1, y¢¢ < 0, кривая выпуклая 1 < x < 0, y¢¢ >0, görbe homorú 0 < x < 1, y¢¢ < 0, кривая выпуклая 1 < x < , y¢¢ >0, görbe homorú < x < ¥, y¢¢ >0, görbe homorú Hiányok felkutatása növekvőés ereszkedő funkciókat. Ehhez meghatározzuk a függvény deriváltjának előjeleit az intervallumokon. -¥ < x < - , y¢ >0, a függvény növekszik - < x < -1, y¢ < 0, функция убывает 1 < x < 0, y¢ < 0, функция убывает 0 < x < 1, y¢ < 0, функция убывает 1 < x < , y¢ < 0, функция убывает < x < ¥, y¢¢ >0, a függvény növekszik Látható, hogy az x = - pont egy pont maximális, és az x = pont a pont minimális. A függvényértékek ezeken a pontokon -3/2 és 3/2. A függőlegesről aszimptoták fentebb már elhangzott. Most keressük meg ferde aszimptoták. Tehát a ferde aszimptota egyenlet y = x. Építsünk menetrend jellemzők: Több változó függvényei
Ha több változó függvényét vizsgáljuk, akkor két változó függvényének részletes leírására szorítkozunk, mivel az összes kapott eredmény érvényes lesz a függvényekre tetszőleges szám változók. Definíció: Ha egy bizonyos halmazhoz tartozó, egymástól független számpárokhoz (x, y) valamilyen szabály szerint hozzárendeljük a z változó egy vagy több értékét, akkor a z változót két változó függvényének nevezzük. . Meghatározás:
Ha egy számpár (x, y) megfelel z egyik értékének, akkor a függvény meghívásra kerül félreérthetetlen, és ha egynél több, akkor - kétértelmű. Meghatározás: A meghatározás hatálya a z függvény azon (x, y) párok halmaza, amelyekre a z függvény létezik. Meghatározás: Szomszédsági pont Az r sugarú M 0 (x 0, y 0) az összes olyan pont (x, y) összessége, amely teljesíti a feltételt Meghatározás:
Az A számot hívják határ az f(x, y) függvény, mint az M(x, y) pont, az M 0 (x 0, y 0) pontra irányul, ha minden e > 0 számra van olyan r > 0, hogy bármelyik M pontra (x, y), amelyre a feltétel a feltétel is igaz Írd le: Meghatározás:
Legyen az M 0 (x 0, y 0) pont az f(x, y) függvény tartományába tartozik. Ekkor a z = f(x, y) függvényt hívjuk meg folyamatos az M 0 (x 0, y 0) pontban, ha sőt az M(x, y) pont tetszőleges módon az M 0 (x 0, y 0) pontba hajlik. Ha az (1) feltétel egyik pontban sem teljesül, akkor ezt a pontot nevezzük töréspontot f(x, y) függvények. Ez a következő esetekben fordulhat elő: 1) A z \u003d f (x, y) függvény nincs definiálva az M 0 (x 0, y 0) pontban. 2) Nincs korlát. 3) Ez a határ létezik, de nem egyenlő f(x 0 , y 0-val). Ingatlan.
Ha az f(x, y, …) függvény definiált és folytonos egy zárt és D határos terület, akkor ezen a területen van legalább egy pont N(x 0 , y 0 , …) úgy, hogy az egyenlőtlenség f(x 0, y 0, …) ³ f(x, y, …) valamint egy N 1 (x 01 , y 01 , ...) pontot úgy, hogy az összes többi pontra igaz az egyenlőtlenség f(x 01 , y 01 , …) £ f(x, y, …) akkor f(x 0, y 0, …) = M – legmagasabb érték függvények, és f(x 01 , y 01 , ...) = m - legkisebb érték f(x, y, …) függvények a D tartományban. Egy folytonos függvény egy zárt és korlátos D tartományban legalább egyszer eléri a legnagyobb értékés egyszer a legkevesebb. Ingatlan.
Ha az f(x, y, …) függvény definiált és folytonos egy zárt korlátos D tartományban, és M és m a függvény legnagyobb és legkisebb értéke ebben a tartományban, akkor bármely m О pontra ott egy pont N 0 (x 0, y 0, …) úgy, hogy f(x 0, y 0, …) = m. Egyszerűen fogalmazva, folyamatos funkció a D régióban veszi az összes köztes értéket M és m között. Ennek a tulajdonságnak az a következménye lehet, hogy ha az M és m számok különböző előjelűek, akkor a D tartományban a függvény legalább egyszer eltűnik. Ingatlan.
f(x, y, …) függvény, folytonos egy zárt korlátos D tartományban, korlátozott ezen a területen, ha van olyan K szám, hogy a terület minden pontjára igaz az egyenlőtlenség Ingatlan.
Ha egy f(x, y, …) függvény definiált és folytonos egy zárt korlátos D tartományban, akkor az egyenletesen folyamatos ezen a területen, i.e. bárkinek pozitív szám e van olyan D > 0 szám, hogy a D-nél kisebb távolságra lévő terület bármely két pontjára (x 1 , y 1) és (x 2 , y 2) az egyenlőtlenség A fenti tulajdonságok hasonlóak egy változó függvényeinek tulajdonságaihoz, amelyek egy intervallumon folytonosak. Lásd: Intervallumonkénti folyamatos funkciók tulajdonságai. Függvények deriváltjai és differenciáljai több változó. Meghatározás.
Legyen adott egy z = f(x, y) függvény valamilyen tartományban. Vegyünk egy tetszőleges M(x, y) pontot, és állítsuk be a Dx növekményt az x változóra. Ekkor a D x z = f(x + Dx, y) – f(x, y) mennyiséget ún. a függvény részleges növelése x-ben. Lehet írni Aztán hívott részleges származéka z = f(x, y) függvények x-ben. Kijelölés: Egy függvény y-hoz viszonyított parciális deriváltját hasonlóan definiáljuk. geometriai érzék a parciális derivált (mondjuk) az N 0 (x 0, y 0, z 0) pontban húzott érintő meredekségének érintője az y \u003d y 0 sík által a felületi metszethez. Teljes növekményés teljes differenciál.
érintő sík Legyenek N és N 0 az adott felület pontjai. Rajzoljunk egy NN 0 egyenest. Az N 0 ponton átmenő síkot ún érintő sík a felületre, ha az NN 0 szekáns és ez a sík közötti szög nullára hajlik, amikor az NN 0 távolság nullára hajlik. Meghatározás. Normál az N 0 pontban lévő felülethez az N 0 ponton átmenő egyenest, amely merőleges a felület érintősíkjára. Egy ponton a felületnek vagy csak egy érintősíkja van, vagy egyáltalán nincs. Ha a felületet a z \u003d f (x, y) egyenlet adja, ahol f (x, y) az M 0 (x 0, y 0) pontban differenciálható függvény, akkor az érintősík az N 0 pontban (x 0, y 0, ( x 0 ,y 0)) létezik, és a következő egyenlete: A felület normáljának egyenlete ezen a ponton: geometriai érzék két változó f (x, y) függvényének teljes differenciáljából az (x 0, y 0) pontban az érintősík felületre vonatkoztatott alkalmazásának (z-koordinátájának) a növekedése a pontból való átmenet során (x 0, y 0) az (x 0 + Dx, y 0 + Dy) pontig. Mint látható, geometriai érzék két változó függvénye teljes differenciáljának térbeli analógja egy változó függvénye differenciáljának geometriai jelentésére. Példa. Határozzuk meg a felület érintősíkjának és normáljának egyenleteit! az M(1, 1, 1) pontban. Érintősík egyenlet: Normál egyenlet: Hozzávetőleges számítások a teljes különbség felhasználásával.
Teljes differenciálmű az u függvény: A kifejezés pontos értéke 1,049275225687319176. Magasabb rendű részleges származékok. Ha az f(x, y) függvény valamilyen D tartományban van definiálva, akkor annak parciális deriváltjai és szintén ugyanabban a tartományban vagy annak egy részében lesz definiálva. Ezeket származékoknak nevezzük elsőrendű parciális származékai. Ezeknek a függvényeknek a származékai lesznek másodrendű parciális származékai. Folytatva a kapott egyenlőségek differenciálását, magasabb rendű parciális deriváltokat kapunk. Tekintsük az y = f(x) függvényt, amelyet az (a, b) intervallumon veszünk figyelembe. Ha meg lehet adni az (a, b) intervallumhoz tartozó x1 pontnak olyan b-szomszédságát, hogy minden x (x1, b) esetén teljesüljön az f(x1) > f(x) egyenlőtlenség, akkor y1 = f1(x1)-et hívjuk funkció maximum y = f(x) lásd az ábrát. Az y = f(x) függvény maximumát max f(x) jelöli. Ha meg lehet adni az (a, b) intervallumhoz tartozó x2 pont 6-os környezetét úgy, hogy minden x esetén O(x2, 6-hoz) tartozik, x nem egyenlő x2-vel, akkor az egyenlőtlenség f(x2)< f(x)
, akkor y2= f(x2)-t az y-f(x) függvény minimumának nevezzük (lásd ábra). Példa a maximum megtalálására, lásd a következő videót Az y = f(x) függvény minimumát min f(x) jelöli. Más szavakkal, egy függvény maximuma vagy minimuma y = f(x) hívottértéke, amely nagyobb (kisebb), mint az összes többi, az adotthoz kellően közeli és attól eltérő ponton vett érték. Megjegyzés 1. Funkció maximum, amelyet az egyenlőtlenség határoz meg, szigorú maximumnak nevezzük; a nem szigorú maximumot az f(x1) > = f(x2) egyenlőtlenség határozza meg 2. megjegyzés. helyi jellegűek (ezek a függvény legnagyobb és legkisebb értékei a megfelelő pont kellően kis környezetében); egyes függvények egyéni minimumai nagyobbak lehetnek, mint ugyanazon függvény maximumai Egy függvény maximumát és minimumát szélsőségnek nevezzük.
. Szélsőségek a keresésben a függvények ábrázolásához latin az extrémum jelentése "szélsőséges"
jelentése. Az x argumentum értékét, amelynél a szélsőértéket elérjük, szélsőpontnak nevezzük. Szükséges állapot szélsőséget a következő tétel fejezi ki. Tétel. A differenciálható függvény és deriváltja szélsőpontjában nulla. A tételnek egyszerű geometriai jelentése van: egy differenciálható függvény grafikonjának érintője a megfelelő pontban párhuzamos az x tengellyel
vagy 
A függvényt hívják antiderivatív funkció. Egy függvény antideriváltja egy állandó értékig van meghatározva.
, itt van egy tetszőleges állandó.
.
, és ez a függvény folytonos és az egyenlőség 
.
ahol .
. Ha felidézzük egy függvény deriváltjának definícióját, és elérjük a határértéket, akkor azt kapjuk, hogy . Vagyis a függvény egyik antideriváltja y = f(x) a szegmensen
. Így az összes antiderivatív halmaza F(x)írható így: , hol TÓL TŐL egy tetszőleges állandó.
, Következésképpen, . Ezt az eredményt használjuk a számításhoz F(b): , vagyis 
. Ez az egyenlőség adja a bizonyítható Newton-Leibniz formulát .
. Ezzel a jelöléssel a Newton-Leibniz képlet a következőt veszi fel.
.Téglalap alakú S.K. Funkció, paraméteresen definiálva Polyarnaya S.K.
Síkfigurák területének számítása
Síkgörbe ívhosszának kiszámítása
A forradalom felületének kiszámítása
nem differenciálegyenlet.
egy matematikai inga nemlineáris egyenletének közelítésének tekinthető 
kis amplitúdók esetén mikor y≈ bűn y.
ahol m- testtömeg, x- a koordinátája, F(x, t) a koordinátájú testre ható erő x akkor t. Megoldása a test pályája a meghatározott erő hatására.
, Funkcióértékek és maximum és minimum pontok
Hogyan kell eljárni ezekben az esetekben? Keresse meg a magas/mélypontot
Így van, először a függvény növekszik, majd csökken – ez a maximum pont!
Válasz: -15 
Válasz: -2 Keresse meg egy függvény legnagyobb / legkisebb értékét
.
.A függvény szélsőértékének lokális jellege
Együtt keressük a funkció szélsőségét
a teljes számegyenesen is létezik. Ezért ebben az esetben csak azok, amelyeknél , azaz kritikus pontként szolgálnak. , honnan és . A kritikus pontokat és a függvény teljes tartományát három monotonitási intervallumra osztjuk: . Mindegyikben kiválasztunk egy-egy vezérlőpontot, és ezen a ponton keressük meg a derivált előjelét.
. Ezért a grafikonja szimmetrikus a tengelyre Oyés a vizsgálat csak az intervallumra végezhető el.
és a funkció kritikus pontjai: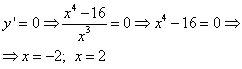
;
,
és határozzuk meg a jelét a következő helyen: kapjuk. Mivel és , akkor a függvény minimumpontja, while 
.
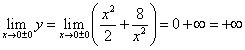
,Továbbra is közösen keressük a függvény szélsőségeit
y y
nál nél
. A ferde aszimptotája y = x.
.
, mert b = konst, akkor 
.
, Következésképpen
.
, akkor 
, Következésképpen
.
.
.
.
(1)
.
.
Funkció minimum
Ennek eredményeként a függvény maximumát (minimumát) hívjuk meg helyi maximum(lokális minimum) ellentétben az abszolút maximummal (minimum) - a legnagyobb (legkisebb) érték a függvény tartományában.