Come determinare il centro di massa di un semicerchio. Posizione del centro di massa

Lezione 4. Centro di gravità.

Questa lezione copre le seguenti domande

1. Centro di gravità corpo solido.

2. Coordinate dei baricentro dei corpi disomogenei.

3. Coordinate dei baricentro dei corpi omogenei.

4. Metodi per determinare le coordinate dei centri di gravità.

5. Baricentro di alcuni corpi omogenei.

Lo studio di questi problemi è necessario in futuro per studiare la dinamica del movimento dei corpi, tenendo conto dell'attrito radente e volvente, della dinamica del movimento del baricentro di un sistema meccanico, dei momenti cinetici, per risolvere i problemi nella disciplina "Forza dei materiali".

Portare forze parallele.

Dopo la riduzione al centro di un sistema piatto e arbitrario sistema spaziale forze, torniamo ancora una volta alla considerazione di un caso particolare di un sistema di forze parallele.

Portare due forze parallele.

Nel corso della considerazione di un tale sistema di forze, sono possibili i seguenti tre casi di riduzione.

1. Sistema di due forze collineari. Consideriamo un sistema di due forze parallele e dirette nella stessa direzione P e Q, applicato ai punti MA e A. Assumiamo che le forze siano perpendicolari a questo segmento (Fig. 1, un).

DA, appartenente al segmento AB e soddisfando la condizione:

corrente alternata/SW = Q/P.(1)

Vettore del sistema principale Rc = P + Q modulo è uguale alla somma di queste forze: Rc = P + Q.

DA tenendo conto (1) è uguale a zero:MC = P ∙ corrente alternata- Q∙ SW = 0.

Quindi, come risultato del cast, abbiamo ottenuto: Rc ≠ 0, MC= 0. Ciò significa che vettore principaleè equivalente alla risultante passante per il centro di riduzione, cioè:

La risultante delle forze collineari è uguale in valore assoluto alla loro somma e la sua linea d'azione divide il segmento che collega i punti della loro applicazione, inversamente proporzionale ai moduli di queste forze internamente.

Si noti che la posizione del punto DA non cambierà se le forze R e Q girare un angoloα. Punto DA, che ha questa proprietà si chiama centro di forze parallele.

2. Sistema di due anticolineare e non uguale nel modulo delle forze. Possano le forze P e Q, applicato ai punti MA e A, parallela, diretta in direzioni opposte e disuguale nel modulo (Fig. 1, b).

Scegliamo il punto come centro di riferimento DA, che soddisfa ancora la relazione (1) e giace sulla stessa retta, ma al di fuori del segmento AB.

Il vettore principale di questo sistema Rc = P + Q modulo sarà ora uguale alla differenza tra i moduli dei vettori: Rc = Q - P.

Momento principale sul centro DAè ancora zero:MC = P ∙ corrente alternata- Q∙ SW= 0, quindi

Risultante anticolineare e forze non uguali in valore assoluto è uguale alla loro differenza, è diretta verso una forza maggiore, e la sua linea d'azione divide il segmento che collega i punti della loro applicazione, inversamente proporzionale ai moduli di queste forze esternamente.

Fig. 1

3. Sistema di due anticolineare e forze uguali in modulo. Prendiamo il precedente caso di riduzione come quello iniziale. Risolviamo il potere R, e forza Q cerchiamo modulo per forzare R.

Poi a Q → R nella formula (1) il rapporto corrente alternata/SW → 1. Questo significa che corrente alternata → SW, cioè la distanza corrente alternata →∞ .

In questo caso, il modulo del vettore principale Rc → 0, e il modulo del momento principale non dipende dalla posizione del centro di riduzione e rimane uguale al valore originario:

MC = P ∙ corrente alternata- Q∙ SW = P ∙ ( corrente alternata- SW) =P ∙ MAB.

Così, al limite, abbiamo ottenuto un sistema di forze per cui Rc = 0, MC≠ 0 e il centro di riduzione viene rimosso all'infinito, che non può essere sostituito dal risultante. In questo sistema, non è difficile scoprire un paio di forze, quindi una coppia di forze non ha risultante.

Centro del sistema di forze parallele.

Considera il sistema n forze Pi, applicato ai puntiAi (x io , si io , z io) e parallela all'asseOv con il vettore l(Fig. 2).

Se escludiamo a priori il caso di un sistema equivalente ad una coppia di forze, non è difficile provare, sulla base del paragrafo precedente, l'esistenza della sua risultanteR.

Determina le coordinate del centroC(X c, y c, z c) forze parallele, cioè le coordinate del punto di applicazione della risultante di questo sistema.

A tale scopo utilizziamo il teorema di Varignon, in base al quale:

M0 (R) = Σ M0(Pi).

Fig.2

Il momento-vettore della forza può essere rappresentato come un prodotto incrociato, quindi:

M 0 (R) = rc× R = Σ M0i(Pi) = Σ ( r io× Pi ).

Dato che R = Rv ∙ l, un Pi = P vi ∙ l e usando le proprietà prodotto vettoriale, noi abbiamo:

rc × Rv ∙ l = Σ ( r io × P vi ∙ l),

rc ∙ R v × l = Σ ( r io ∙ P vi × l) = Σ ( r io ∙ P vi ) × l,

[ r c R v - Σ ( r io P vi )] × l= 0.

L'ultima espressione è valida solo se l'espressione tra parentesi quadre è zero. Pertanto, omettendo l'indiceve considerando che la risultanteR = Σ Pi , da qui otteniamo:

rc = (Σ Pi r io )/(Σ Pi ).

Proiettando l'ultima uguaglianza del vettore sull'asse delle coordinate, otteniamo il desiderato espressione delle coordinate del centro di forze parallele:

xc = (Σ Pi x io)/(Σ Pi );

e c = (Σ Pi si io )/(Σ Pi );(2)

zc = (Σ Pi z io )/(Σ Pi ).

Centro di gravità del corpo

Coordinate dei centri di gravità di un corpo omogeneo.

Considera un corpo rigido che pesa P e volume V nel sistema di coordinate Oxyz, dove gli assi X e y connesso con la superficie terrestre e l'asse z diretto allo zenit.

Se spezziamo il corpo in parti elementari con un volume∆ V io , allora la forza di attrazione agirà su ciascuna parte di essa∆ Pidiretto verso il centro della terra. Assumiamo che le dimensioni del corpo siano molto più piccole delle dimensioni della Terra, quindi il sistema di forze applicato alle parti elementari del corpo può essere considerato non convergente, ma parallelo (Fig. 3), e tutte le conclusioni del capitolo precedente sono ad esso applicabili.

Fig.3

Definizione . Il baricentro di un corpo rigido è il centro delle forze di gravità parallele delle parti elementari di questo corpo.

Richiama questo peso specifico parte elementare del corpo è chiamata rapporto tra il suo peso∆ Pi al volume ∆ V io : γ io = ∆ Pi/ ∆ V io . Per un corpo omogeneo, questo valore è costante:γ io = γ = P/ V.

Sostituendo in (2) ∆ Pi = γ io ∙∆ V io invece di Pi, tenendo conto dell'ultima osservazione e riducendo numeratore e denominatore dig, noi abbiamo espressioni per le coordinate del baricentro di un corpo omogeneo:

xc = (Σ ∆ Vi∙ x io)/(Σ ∆ Vi);

e c = (Σ ∆ Vi∙ si io )/(Σ ∆ Vi);(3)

zc = (Σ ∆ Vi∙ z io )/(Σ ∆ Vi).

Diversi teoremi sono utili per determinare il baricentro.

1) Se un corpo omogeneo ha un piano di simmetria, allora il suo centro di gravità è su questo piano.

Se gli assi X e a posto in questo piano di simmetria, quindi per ogni punto con coordinate. e coordinare secondo (3), sarà uguale a zero, perché in totale tutto i termini con segni opposti vengono eliminati a coppie. Quindi il centro di gravità è nel piano di simmetria.

2) Se un corpo omogeneo ha un asse di simmetria, il baricentro del corpo si trova su questo asse.

Infatti, in questo caso, se l'assezdisegnare lungo l'asse di simmetria, per ogni punto con coordinatepuoi trovare un punto con le coordinate e coordinate e calcolato con le formule (3) sarà uguale a zero.

Il terzo teorema è dimostrato in modo simile.

3) Se un corpo omogeneo ha un centro di simmetria, allora il baricentro del corpo si trova in questo punto.

E qualche altra osservazione.

Primo. Se il corpo può essere diviso in parti di cui si conosce il peso e la posizione del baricentro, non è necessario considerare ogni punto, ma nelle formule (3) Pi – da determinare come peso della parte rilevante ecome coordinate del suo baricentro.

Secondo. Se il corpo è omogeneo, allora il peso di una parte separata di esso, dove è il peso specifico del materiale di cui è fatto il corpo, e Vi - il volume di questa parte del corpo. E le formule (3) assumeranno una forma più conveniente. Per esempio,

E allo stesso modo, dove - il volume di tutto il corpo.

Terza nota. Lascia che il corpo assomigli a un piatto sottile con area F e spessore t sdraiato sull'aereo Ossi. Sostituendo in (3)∆ V io =t ∙ ∆F io , otteniamo le coordinate del baricentro di una lastra omogenea:

xc = (Σ ∆ F io∙ x io) / (Σ ∆ F io);

e c = (Σ ∆ F io∙ si io ) / (Σ ∆ F io).

zc = (Σ ∆ F io∙ z io ) / (Σ ∆ F io).

dove – coordinate del baricentro dei singoli piatti;è l'area totale del corpo.

Quarta nota. Per un corpo a forma di sottile asta curvilinea con una lunghezza l con area della sezione trasversale un volume elementare∆ V io = un ∙∆ l io , Ecco perchè coordinate del baricentro di una sottile asta curvilinea sarà uguale:

xc = (Σ ∆ L io∙ x io)/(Σ ∆ L io);

e c = (Σ ∆ L io∙ si io )/(Σ ∆ L io);(4)

zc = (Σ ∆ L io∙ z io )/(Σ ∆ L io).

dove – coordinate del baricentroio-esima sezione; .

Si noti che secondo la definizione, il baricentro è un punto geometrico; potrebbe trovarsi fuori dato corpo(ad esempio, per un anello).

Nota.

In questa sezione del corso, non distinguiamo tra gravità, gravità e peso corporeo. In realtà, la gravità è la differenza tra la gravità terrestre e la forza centrifuga causata dalla sua rotazione.

Coordinate dei centri di gravità dei corpi disomogenei.

Coordinate del centro di gravità solido disomogeneo(Fig. 4) nel sistema di riferimento selezionato sono definiti come segue:

Fig.4

dove - peso per unità di volume corporeo (peso specifico)

- tutto il peso corporeo.

superficie irregolare(Fig. 5), quindi le coordinate del baricentro nel sistema di riferimento selezionato sono determinate come segue:

Fig.5

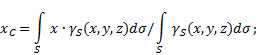
dove - peso per unità di area del corpo

- tutto il peso corporeo.

Se il solido è linea eterogenea(Fig. 6), quindi le coordinate del baricentro nel sistema di riferimento selezionato sono determinate come segue:

Fig.6

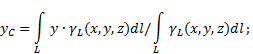
dove - peso unitario di lunghezza del corpo,

Tutto il peso del corpo.

Metodi per determinare le coordinate del baricentro.

Sulla base delle formule generali sopra ottenute, è possibile indicare metodi specifici determinare le coordinate dei centri di gravità dei corpi.

1. Simmetria. Se un corpo omogeneo ha un piano, un asse o un centro di simmetria (Fig. 7), il suo centro di gravità si trova rispettivamente nel piano di simmetria, nell'asse di simmetria o nel centro di simmetria.

Fig.7

2. Scissione. Il corpo è suddiviso in un numero finito di parti (Fig. 8), per ciascuna delle quali è nota la posizione del baricentro e l'area.

Fig.8

S \u003d S 1 + S 2.

3.Metodo delle aree negative. Un caso speciale del metodo di partizionamento (Fig. 9). Si applica ai corpi con intagli se sono noti i baricentro del corpo senza l'intaglio e l'intaglio. Un corpo a forma di piatto con un ritaglio è rappresentato da una combinazione di un piatto solido (senza un ritaglio) con un'area S1 e l'area della parte ritagliata S2.

Fig.9

S \u003d S 1 - S 2.

4.metodo di raggruppamento.È una buona aggiunta agli ultimi due metodi. Dopo aver scomposto la figura nei suoi elementi costitutivi, può essere conveniente ricombinarne alcuni, in modo da semplificare poi la soluzione tenendo conto della simmetria di questo gruppo.

Centri di gravità di alcuni corpi omogenei.

1) Centro di gravità di un arco di cerchio. Considera l'arco AB raggioR con angolo centrale. A causa della simmetria, il baricentro di questo arco giace sull'asseBue(Fig. 10).

Fig.10

Troviamo la coordinata secondo la formula . Per fare ciò, seleziona sull'arco AB elemento MM ’ lungo, la cui posizione è determinata dall'angolo. Coordinata X elemento MM' sarà. Sostituendo questi valori X e d l e tenendo presente che l'integrale deve essere esteso per tutta la lunghezza dell'arco, si ottiene:

dove L è la lunghezza dell'arco AB uguale a .

Da qui troviamo infine che il baricentro dell'arco circolare giace sul suo asse di simmetria ad una distanza dal centro Oh uguale

dov'è l'angolo misurata in radianti.

2) Il baricentro dell'area di un triangolo. Considera un triangolo che giace nel piano Ossi, le cui coordinate di vertice sono note: Ai (x io,si io ), (io= 1,2,3). Spezzare il triangolo in strisce sottili parallele al lato MA 1 MA 2 , giungiamo alla conclusione che il baricentro del triangolo deve appartenere alla mediana MA 3 M 3 (fig.11) .

Fig.11

Spezzare il triangolo in strisce parallele al lato MA 2 MA 3 , puoi assicurarti che si trovi sulla mediana MA 1 M uno . In questo modo, il baricentro di un triangolo si trova nel punto di intersezione delle sue mediane, che, come sapete, separa la terza parte da ciascuna mediana, contando dal lato corrispondente.

In particolare per la mediana MA 1 M 1 otteniamo, dato che le coordinate del punto M 1 - è la media aritmetica delle coordinate dei vertici MA 2 e MA 3 :

xc = X 1 + (2/3) ∙ (XM 1 - X 1 ) = X 1 + (2/3) ∙ [(X 2 + X 3 )/2 - X 1 ] = (X 1 + X 2 + X 3 )/3.

Pertanto, le coordinate del baricentro del triangolo sono la media aritmetica delle coordinate dei suoi vertici:

X c =(1/3) Σ x io ; y c =(1/3) Σ si io .

3) Il baricentro dell'area del settore circolare. Considera un settore di una circonferenza di raggio R con angolo centrale 2α , posizionato simmetricamente rispetto all'asse Bue (Fig. 12) .

È ovvio che y c = 0, e la distanza dal centro del cerchio da cui questo settore è tagliato al suo baricentro può essere determinata dalla formula:

Fig.12

Il modo più semplice per calcolare questo integrale è dividere il dominio di integrazione in settori elementari con un angolo dφ . Fino a infinitesimi del primo ordine, tale settore può essere sostituito da un triangolo di base uguale a R × dφ e altezza R. L'area di un tale triangolo dF =(1/2)R 2 ∙ dφ e il suo centro di gravità è 2/3 R dall'alto, quindi in (5) mettiamo X = (2/3)R∙ cos. Sostituendo in (5) F= α R 2 otteniamo:

Utilizzando l'ultima formula, calcoliamo, in particolare, la distanza dal baricentro semicerchio.

Sostituendo in (2) α = π /2, otteniamo: X c = (4 R)/(3 π ) ≅ 0,4 R .

Esempio 1Determiniamo il baricentro del corpo omogeneo mostrato in Fig. 13.

Fig.13

Soluzione.Il corpo è omogeneo, costituito da due parti di forma simmetrica. Le coordinate dei loro centri di gravità:

I loro volumi:

Pertanto, le coordinate del baricentro del corpo

Esempio 2 Trova il baricentro di un piatto piegato ad angolo retto. Dimensioni - sul disegno (Fig. 14).

Fig.14

Soluzione. Coordinate dei centri di gravità:

Piazze:

Ecco perchè:

Esempio 3 Su un foglio quadrato foro quadrato tagliato cm vedere (Fig. 15). Trova il baricentro del foglio. Esempio 4 Trovare la posizione del baricentro della piastra mostrata in fig. 16. Le dimensioni sono espresse in centimetri.

Fig.16

Soluzione. Dividiamo il piatto in figure (Fig. 17), centri la cui gravità è nota.

Le aree di queste figure e le coordinate dei loro centri di gravità:

1) un rettangolo di lato 30 e 40 cm,S 1 =30 ∙ 40=1200 cm 2 ; x 1=15 cm; a 1 \u003d 20 cm.

2) un triangolo rettangolo con base di 50 cm e altezza di 40 cm;S 2 =0,5 ∙ 50 ∙ 40= 1000 cm 2 ; X 2 \u003d 30 + 50 / 3 \u003d 46,7 cm; si 2 =40/3 =13,3 cm;

3) raggio del cerchio di semicerchio r = 20 cm;S 3 =0,5 ∙π∙ 20 2 \u003d 628 cm 2 ; X 3 =4 R /3 π =8,5 cm; a

Soluzione. Ricordiamo che in fisica la densità di un corpoρ e il suo peso specificoglegati dal rapporto:γ = ρ g , doveg - accelerazione caduta libera. Per trovare la massa di un corpo così omogeneo, devi moltiplicare la densità per il suo volume.

Fig.19

Il termine densità "lineare" o "lineare" significa che per determinare la massa del truss rod, la densità lineare deve essere moltiplicata per la lunghezza di questo tondino.

Per risolvere il problema, puoi utilizzare il metodo di partizionamento. Rappresentando un dato traliccio come somma di 6 singole aste, otteniamo:

doveL io lunghezzaio -th asta della fattoria, ex io , si io - coordinate del suo baricentro.

La soluzione a questo problema può essere semplificata raggruppando gli ultimi 5 truss rod. È facile vedere che formano una figura con un centro di simmetria situato nel mezzo della quarta asta, dove si trova il baricentro di questo gruppo di aste.

Pertanto, un determinato traliccio può essere rappresentato da una combinazione di soli due gruppi di aste.

Il primo gruppo è costituito dalla prima canna, per questol 1 = 4 m,X 1 = 0 m,y 1 = 2 M. Il secondo gruppo di aste è composto da cinque aste, per le qualil 2 = 20 m,X 2 = 3 m,y 2 = 2 m.

Le coordinate del baricentro della fattoria si trovano con la formula:

X c = (l 1 ∙ X 1 + l 2 ∙ X 2 )/(l 1 + l 2 ) = (4∙0 + 20∙3)/24 = 5/2 m;

y c = (l 1 ∙ y 1 + l 2 ∙ y 2 )/(l 1 + l 2 ) = (4∙2 + 20∙2)/24 = 2 m.

Si noti che il centro DA giace sulla linea di collegamento DA 1 e DA 2 e divide il segmento DA 1 DA 2 in merito a: DA 1 DA/SS 2 = (X c - X 1 )/(X 2 - X c ) = l 2 / l 1 = 2,5/0,5.

Domande per l'autoesame

Qual è il centro delle forze parallele?

- Come vengono determinate le coordinate del centro delle forze parallele?

- Come determinare il centro delle forze parallele, la cui risultante è zero?

Qual è la proprietà del centro delle forze parallele?

- Quali formule vengono utilizzate per calcolare le coordinate del centro delle forze parallele?

Qual è il baricentro di un corpo?

- Perché le forze di attrazione della Terra, agenti su un punto del corpo, possono essere assunte come un sistema di forze parallele?

- Scrivere la formula per determinare la posizione del baricentro di corpi disomogenei e omogenei, la formula per determinare la posizione del baricentro di sezioni piane?

- Annotare la formula per determinare la posizione del baricentro del semplice forme geometriche: rettangolo, triangolo, trapezio e semicerchio?

Come si chiama il momento statico dell'area?

- Fornisci un esempio di un corpo il cui baricentro si trova all'esterno del corpo.

- Come vengono utilizzate le proprietà di simmetria per determinare i centri di gravità dei corpi?

- Qual è l'essenza del metodo dei pesi negativi?

Dove si trova il baricentro dell'arco circolare?

- Come costruzione grafica riesci a trovare il baricentro del triangolo?

- Annotare la formula che determina il baricentro del settore circolare.

- Utilizzando le formule che determinano i centri di gravità di un triangolo e di un settore circolare, ricavare una formula simile per un segmento circolare.

- Quali formule vengono utilizzate per calcolare le coordinate dei baricentro di corpi omogenei, figure piatte e linee?

- Qual è il momento statico dell'area di una figura piatta rispetto all'asse, come viene calcolato e che dimensione ha?

- Come determinare la posizione del baricentro dell'area, se è nota la posizione dei baricentro delle sue singole parti?

- Quali teoremi ausiliari vengono utilizzati per determinare la posizione del baricentro?

La tecnica matematica del calcolo del baricentro appartiene al campo dei corsi di matematica; lì tali problemi servono come buoni esempi nel calcolo integrale. Ma anche se sai integrare, è utile conoscere alcuni trucchi per calcolare la posizione del baricentro. Uno di questi trucchi si basa sull'uso del cosiddetto teorema di Pappo, che funziona come segue. Se prendiamo una figura chiusa e formiamo un corpo rigido ruotando questa figura nello spazio in modo che ogni punto si muova perpendicolarmente al piano della figura, allora il volume del corpo formato in questo caso è uguale al prodotto dell'area di la figura e la distanza percorsa dal suo baricentro! Naturalmente questo teorema vale anche nel caso in cui una figura piatta si muova lungo una retta perpendicolare alla sua area, ma se la muoviamo lungo una circonferenza o altro

curva, poi risulta molto di più corpo interessante. Quando si guida su un sentiero tortuoso parte interna la figura avanza meno di quella esterna e questi effetti si annullano a vicenda. Quindi se vogliamo definire; il baricentro di una figura piana con densità uniforme, quindi va ricordato che il volume formato dalla sua rotazione attorno all'asse è uguale alla distanza percorsa dal baricentro, moltiplicata per l'area di \u200b\ u200bla cifra.
Ad esempio, se dobbiamo trovare il centro di massa triangolo rettangolo con base D e altezza H (Fig. 19.2), si procede come segue. Immagina un asse lungo H e ruota il triangolo di 360° attorno a quell'asse. Questo ci dà un cono. La distanza percorsa dalla coordinata x del centro di massa è 2πx e l'area della regione che si è mossa, ovvero l'area del triangolo, è pari a l/2 HD. Il prodotto della distanza percorsa dal centro di massa e dall'area del triangolo è uguale al volume del cono, ovvero 1/3 πD 2 H. Quindi, (2πх) (1/2HD) = 1/3D 2 H, oppure x= D/З. Allo stesso modo, ruotando attorno alla seconda gamba, o semplicemente per motivi di simmetria, troviamo che y \u003d H / 3. In generale, il centro di massa di ogni triangolo omogeneo si trova nel punto di intersezione delle sue tre mediane (linee che collegano la sommità del triangolo con il punto medio del lato opposto), che è ad una distanza dalla base pari a 1/ 3 della lunghezza di ciascuna mediana.
Come vederlo? Taglia il triangolo con le linee parallele alla base in tante strisce. Si noti ora che la mediana divide in due ogni striscia, quindi il centro di massa deve trovarsi sulla mediana.
Prendiamo ora una figura più complessa. Assumiamo che sia necessario trovare la posizione del baricentro di un semicerchio omogeneo, cioè un cerchio tagliato a metà. Dove si troverà il baricentro in questo caso? Per un cerchio completo, il centro di massa si trova a centro geometrico, ma per un semicerchio trovare la sua posizione è più difficile. Sia r il raggio della circonferenza e x la distanza del centro di massa dal confine rettilineo del semicerchio. Ruotandolo attorno a questo bordo come attorno a un asse, otteniamo una palla. In questo caso, il centro di massa percorre una distanza di 2πx e l'area del semicerchio è 1/2πr 2 (metà dell'area del cerchio). Poiché il volume della sfera è, ovviamente, 4πg 3 /3, da qui troviamo

C'è un altro teorema di Pappo, che è in realtà un caso speciale del teorema sopra formulato, e quindi è anche valido. Supponiamo che invece di un semicerchio solido abbiamo preso un semicerchio, ad esempio un pezzo di filo a forma di semicerchio con una densità uniforme, e vogliamo trovarne il centro di massa. Si scopre che l'area che viene "percorsa" da una curva piatta quando si sposta, simile a quella sopra descritta, è uguale alla distanza percorsa dal centro di massa, moltiplicata per la lunghezza di questa curva. (La curva può essere pensata come una striscia molto stretta e il teorema precedente applicato ad essa.)

Centro di gravità di un arco di cerchio

L'arco ha un asse di simmetria. Il baricentro giace su questo asse, cioè y C = 0 .

dl– elemento ad arco, dl = Rdφ, Rè il raggio del cerchio, x = Rcosφ, L= 2aR,

Di conseguenza:

X C = R(sinα/α).

Baricentro del settore circolare

settore del raggio R con angolo centrale 2 α ha un asse di simmetria Bue dove si trova il baricentro.

Dividiamo il settore in settori elementari, che possono essere considerati triangoli. I centri di gravità dei settori elementari si trovano sull'arco di un cerchio di raggio (2/3) R.

Il baricentro del settore coincide con il baricentro dell'arco AB:

Semicerchio:

37. Cinematica. Cinematica dei punti. Metodi per specificare il movimento di un punto.

Cinematica branca della meccanica che si occupa del movimento corpi materiali da un punto di vista geometrico, senza tener conto della massa e delle forze che agiscono su di esse. Metodi per specificare il movimento di un punto: 1) naturale, 2) coordinata, 3) vettore.

Cinematica dei punti- una sezione di cinematica che studia descrizione matematica movimento di punti materiali. Il compito principale della cinematica è descrivere il movimento con l'aiuto di un apparato matematico senza scoprire le ragioni che causano questo movimento.

terme naturali. viene indicata la traiettoria del punto, la legge del suo movimento lungo questa traiettoria, l'inizio e la direzione della coordinata dell'arco: s=f(t) – la legge del movimento del punto. Per moto rettilineo: x=f(t).

Coordinato sp. la posizione di un punto nello spazio è determinata da tre coordinate, le cui variazioni determinano la legge di moto del punto: x=f 1 (t), y=f 2 (t), z=f 3 (t).

Se il moto è in un piano, allora ci sono due equazioni del moto. Le equazioni del moto descrivono l'equazione della traiettoria in forma parametrica. Eliminando il parametro t dalle equazioni, otteniamo l'equazione della traiettoria nella forma usuale: f (x, y) = 0 (per un piano).

Stazione termale vettoriale. la posizione di un punto è determinata dal suo vettore raggio disegnato da un centro. Una curva disegnata dalla fine di un vettore, chiamata. odografo questo vettore. Quelli. la traiettoria è l'odografo del raggio vettore.

38. Collegamento tra coordinata e vettore, coordinate e modi naturali per specificare il movimento di un punto.

RAPPORTO DEL METODO VETTORIALE CON LE COORDINATE E IL NATURALEè espresso dalle relazioni:

dove è il vettore unitario della tangente alla traiettoria in un dato punto, diretto verso la lettura della distanza, è il vettore unitario della normale alla traiettoria in un dato punto, diretto verso il centro di curvatura (vedi Fig. 3).

RAPPORTO DEL METODO COORDINATO CON IL NATURALE. Equazione della traiettoria f(x, y)=z; f 1 (x, z)=y si ottiene dalle equazioni del moto in forma coordinata eliminando il tempo t. Un'ulteriore analisi dei valori che possono assumere le coordinate di un punto determina quella sezione della curva, che è una traiettoria. Ad esempio, se il movimento di un punto è dato dalle equazioni: x=sin t; y=sin 2 t=x 2 , allora la traiettoria del punto è quella sezione della parabola y=x 2 per cui -1≤x≤+1, 0≤x≤1. L'inizio e la direzione del conteggio delle distanze sono scelti arbitrariamente, questo determina ulteriormente il segno della velocità e la grandezza e il segno della distanza iniziale s 0 .

La legge del moto è determinata dalla dipendenza:

il segno + o - è determinato a seconda della direzione accettata delle distanze di conteggio.

Velocità di puntaè una misura cinematica del suo moto, uguale alla derivata temporale del vettore raggio di questo punto nel sistema di riferimento in esame. Il vettore velocità è diretto tangenzialmente alla traiettoria del punto nella direzione del movimento

Vettore di velocità (v)è la distanza che un corpo percorre in una certa direzione nell'unità di tempo. Si noti che la definizione vettore di velocità molto simile alla determinazione della velocità, tranne per una differenza importante: la velocità di un corpo non indica la direzione del movimento, ma il vettore di velocità di un corpo indica sia la velocità che la direzione del movimento. Pertanto, sono necessarie due variabili che descrivono il vettore di velocità del corpo: velocità e direzione. Le grandezze fisiche che hanno un significato e una direzione sono dette grandezze vettoriali.

vettore di velocità il corpo può cambiare di volta in volta. Se cambia la sua velocità o direzione, cambia anche la velocità del corpo. Un vettore a velocità costante implica una velocità e una direzione costanti, mentre il termine "velocità costante" implica solo un valore costante, indipendentemente dalla direzione. Il termine "vettore di velocità" è spesso usato in modo intercambiabile con il termine "velocità". Entrambi esprimono la distanza che il corpo percorre nell'unità di tempo.

accelerazione puntiformeè una misura della variazione della sua velocità, uguale alla derivata temporale della velocità di questo punto o alla derivata seconda del raggio vettore del punto nel tempo. L'accelerazione caratterizza la variazione del vettore velocità in magnitudine e direzione ed è diretta verso la concavità della traiettoria.

vettore di accelerazione

è il rapporto tra la variazione di velocità e l'intervallo di tempo durante il quale si è verificata questa variazione. L'accelerazione media può essere determinata dalla formula:

dove - vettore di accelerazione.

La direzione del vettore di accelerazione coincide con la direzione della variazione di velocità Δ = - 0 (qui 0 è la velocità iniziale, cioè la velocità alla quale il corpo ha iniziato ad accelerare).

All'istante t1 (vedi Figura 1.8) il corpo ha una velocità di 0 . All'istante t2 il corpo ha una velocità. Secondo la regola di sottrazione del vettore, troviamo il vettore della variazione di velocità Δ = - 0 . Quindi l'accelerazione può essere definita come segue:

Centri di gravità di alcune semplici forme geometriche

Per determinare i centri di gravità di corpi di forma frequente (triangolo, arco circolare, settore, segmento), è conveniente utilizzare i dati di riferimento (vedi tabella).

Coordinate del baricentro di alcuni corpi omogenei

№	Nome della figura	Immagine
	arco di cerchio: il baricentro di un arco di circonferenza omogenea è sull'asse di simmetria (coordinata c Rè il raggio del cerchio.
	Settore circolare omogeneo c= 0). dove α è la metà dell'angolo centrale; Rè il raggio del cerchio.
	Segmento: il baricentro si trova sull'asse di simmetria (coordinata c= 0). dove α è la metà dell'angolo centrale; Rè il raggio del cerchio.
	Semicerchio:
	Triangolo: il baricentro di un triangolo omogeneo si trova nel punto di intersezione delle sue mediane. dove x1, y1, x2, y2, x3, y3 sono le coordinate dei vertici del triangolo
	Cono: il baricentro di un cono circolare omogeneo giace alla sua altezza ed è ad una distanza di 1/4 dell'altezza dalla base del cono.
	emisfero: il baricentro giace sull'asse di simmetria.
	Trapezio: è l'area della figura.
	- l'area della figura;

Sotto il baricentro dell'auto si assume un punto condizionale, in cui si concentra tutto il suo peso. La posizione del baricentro ha un impatto significativo sulla maneggevolezza e stabilità del veicolo e il conducente deve sempre tenerne conto. La posizione del baricentro in altezza dipende dal peso e dalla natura del carico. Ad esempio, se un'autovettura trasporta merci che si trovano solo nella carrozzeria, il suo baricentro sarà molto più basso rispetto a quando si trasporta merci su un bagagliaio che si trova sopra il tetto. Tuttavia, indipendentemente dalla natura del carico e dalla sua collocazione, il baricentro di una macchina carica sarà sempre più alto di quello di una macchina scarica. In considerazione di ciò, l'opinione esistente di molti conducenti sulla buona stabilità di un veicolo carico (e ancor di più sulla riduzione della probabilità di ribaltamento) non è corretta.

L'altezza del baricentro della macchina influisce sulla ridistribuzione delle normali reazioni sulle ruote durante l'accelerazione e la frenata, nonché durante l'inclinazione della macchina, che si rifletterà nella massa di trazione e, di conseguenza, nella forza di trazione massima.

La posizione del baricentro del veicolo è Grande importanza. Caratterizza la stabilità della macchina contro il ribaltamento. Questo è chiaramente visualizzato negli autobus con passeggeri in piedi ed è anche più rilevante per le auto (autotreni) che trasportano merci di grandi dimensioni, furgoni e veicoli speciali veicoli da trasporto(autotorri, autogru, ecc.).

6.1. Informazione Generale

Centro di forze parallele
Si considerino due forze parallele dirette nella stessa direzione , e , applicate al corpo nei punti MA 1 e MA 2 (fig.6.1). Questo sistema di forze ha una risultante, la cui linea d'azione passa per un certo punto DA. Posizione del punto DA può essere trovato usando il teorema di Varignon:

Se giri la forza e ti avvicini ai punti MA 1 e MA 2 in una direzione e con lo stesso angolo, otteniamo nuovo sistema grassi paralleli aventi gli stessi moduli. In questo caso, anche la loro risultante passerà attraverso il punto DA. Tale punto è chiamato centro di forze parallele.
Si consideri un sistema di forze parallele ed egualmente dirette applicate a un corpo rigido in punti. Questo sistema ha una risultante.
Se ciascuna forza del sistema viene ruotata vicino ai punti della loro applicazione nella stessa direzione e allo stesso angolo, si otterranno nuovi sistemi di forze parallele egualmente dirette con gli stessi moduli e punti di applicazione. Il risultante di tali sistemi avrà lo stesso modulo R, ma ogni volta in una direzione diversa. Deposto la forza F 1 e F 2 trovano che la loro risultante R 1 , che passerà sempre per il punto DA 1, la cui posizione è determinata dall'uguaglianza. Aggiungendo ulteriormente R 1 e F 3 , trova la loro risultante, che passerà sempre per il punto DA 2 sdraiato sulla linea MA 3 DA 2. Avendo portato a termine il processo di addizione delle forze, giungeremo alla conclusione che la risultante di tutte le forze passerà infatti sempre per lo stesso punto DA, la cui posizione rispetto ai punti rimarrà invariata.
Punto DA, attraverso la quale passa la linea d'azione del sistema risultante di forze parallele per ogni rotazione di queste forze vicino ai punti della loro applicazione nella stessa direzione allo stesso angolo è chiamata centro delle forze parallele (Fig. 6.2).

Fig.6.2

Determiniamo le coordinate del centro delle forze parallele. Dalla posizione del punto DA rispetto al corpo è invariato, quindi le sue coordinate non dipendono dalla scelta del sistema di coordinate. Ruotare tutte le forze vicino alla loro applicazione in modo che diventino parallele all'asse UO e applica il teorema di Varignon alle forze ruotate. Perché R"è la risultante di queste forze, quindi, secondo il teorema di Varignon, abbiamo , perché , , noi abbiamo

Da qui troviamo la coordinata del centro delle forze parallele zc:

Per determinare la coordinata xc comporre un'espressione per il momento delle forze attorno all'asse Oz.

Per determinare la coordinata yc ruotare tutte le forze in modo che diventino parallele all'asse Oz.

La posizione del centro delle forze parallele rispetto all'origine (Fig. 6.2) può essere determinata dal suo vettore raggio:

6.2. Baricentro di un corpo rigido

centro di gravità di un corpo rigido è un punto invariabilmente associato a questo corpo DA, attraverso la quale passa la linea d'azione della risultante delle forze di gravità di un dato corpo, per qualsiasi posizione del corpo nello spazio.
Il baricentro viene utilizzato nello studio della stabilità delle posizioni di equilibrio di corpi e mezzi continui sotto l'azione della gravità e in alcuni altri casi, ovvero: nella resistenza dei materiali e nella meccanica strutturale- quando si utilizza la regola Vereshchagin.
Esistono due modi per determinare il baricentro di un corpo: analitico e sperimentale. Il metodo analitico per la determinazione del baricentro deriva direttamente dal concetto di centro di forze parallele.
Le coordinate del baricentro, come centro delle forze parallele, sono determinate dalle formule:

dove R- peso di tutto il corpo; pk- peso delle particelle corporee; xk, yk, zk- coordinate delle particelle corporee.
Per un corpo omogeneo, il peso di tutto il corpo e di qualsiasi sua parte è proporzionale al volume P=Vγ, pk =vk γ, dove γ - peso per unità di volume, V- volume del corpo. Espressioni sostitutive P, pk nelle formule per determinare le coordinate del baricentro e, riducendo di un fattore comune γ , noi abbiamo:

Punto DA, le cui coordinate sono determinate dalle formule ottenute il baricentro del volume.
Se il corpo è magro piatto omogeneo, allora il baricentro è determinato dalle formule:

dove S- area dell'intero piatto; sk- l'area da parte sua; xk, yk- coordinate del baricentro delle parti in lamiera.
Punto DA in questo caso viene chiamato zona del baricentro.
Si chiamano con i numeratori delle espressioni che determinano le coordinate del baricentro delle figure piane momenti statici del territorio sugli assi a e X:

Quindi il baricentro dell'area può essere determinato dalle formule:

Per i corpi la cui lunghezza è molte volte maggiore delle dimensioni della sezione trasversale, viene determinato il baricentro della linea. Le coordinate del baricentro della linea sono determinate dalle formule:

dove l- lunghezza della linea; lc- la lunghezza delle sue parti; xk, yk, zk- coordinata del baricentro delle parti di linea.

6.3. Metodi per determinare le coordinate dei centri di gravità dei corpi

Sulla base delle formule ottenute, è possibile proporre metodi pratici per determinare i baricentro dei corpi.
1. Simmetria. Se il corpo ha un centro di simmetria, allora il centro di gravità è al centro di simmetria.
Se il corpo ha un piano di simmetria. Ad esempio, il piano XOU, quindi il centro di gravità si trova in questo piano.
2. scissione. Per i corpi costituiti da corpi semplici, viene utilizzato il metodo di divisione. Il corpo è diviso in parti, il cui centro di gravità si trova con il metodo della simmetria. Il baricentro dell'intero corpo è determinato dalle formule per il baricentro del volume (area).

Esempio. Determinare il baricentro della piastra mostrato nella figura sottostante (Fig. 6.3). Il piatto può essere diviso in rettangoli in un altro modo e determinare le coordinate del baricentro di ciascun rettangolo e la loro area.

Fig.6.3

Risposta: Xc= 17,0 cm; yc= 18,0 cm.

3. Aggiunta. Questo metodo è un caso speciale del metodo di partizionamento. Viene utilizzato quando il corpo presenta intagli, tagli, ecc., se si conoscono le coordinate del baricentro del corpo senza l'intaglio.

Esempio. Determinare il baricentro di una piastra rotonda avente un ritaglio con un raggio r = 0,6 R(Fig. 6.4).

Fig.6.4

La piastra rotonda ha un centro di simmetria. Posizioniamo l'origine delle coordinate al centro del piatto. Area della piastra senza tacca, area della tacca. Area della piastra dentellata; .
La piastra dentata ha un asse di simmetria O1 x, Di conseguenza, yc=0.

4. Integrazione. Se il corpo non può essere diviso in un numero finito di parti, di cui sono note le posizioni dei baricentro, il corpo viene diviso in piccoli volumi arbitrari, per i quali la formula che utilizza il metodo di partizione assume la forma: .
Inoltre passano al limite, tendendo a zero i volumi elementari, cioè contrazione dei volumi in punti. Le somme vengono sostituite da integrali estesi all'intero volume del corpo, quindi le formule per determinare le coordinate del baricentro del volume assumono la forma:

Formule per determinare le coordinate del baricentro dell'area:

Le coordinate del baricentro dell'area devono essere determinate studiando l'equilibrio delle piastre, quando si calcola l'integrale di Mohr in meccanica strutturale.

Esempio. Determina il baricentro di un arco di cerchio di raggio R con angolo centrale AOB= 2α (Fig. 6.5).

Riso. 6.5

L'arco di cerchio è simmetrico all'asse Oh, quindi, il baricentro dell'arco giace sull'asse Oh, yc = 0.
Secondo la formula per il baricentro di una linea:

6.Modo sperimentale. I centri di gravità di corpi disomogenei di configurazione complessa possono essere determinati sperimentalmente: appendendo e pesando. Il primo modo è che il corpo sia sospeso su un cavo in vari punti. La direzione della fune su cui è sospeso il corpo darà la direzione della gravità. Il punto di intersezione di queste direzioni determina il baricentro del corpo.
Il metodo di pesatura consiste nel determinare prima il peso di un corpo, come un'auto. Quindi, sulla bilancia, viene determinata la pressione dell'asse posteriore dell'auto sul supporto. Compilando un'equazione di equilibrio rispetto a un punto, ad esempio l'asse delle ruote anteriori, puoi calcolare la distanza da questo asse al baricentro dell'auto (Fig. 6.6).

Fig.6.6

A volte, quando si risolvono i problemi, è necessario applicare contemporaneamente metodi diversi per determinare le coordinate del baricentro.

6.4. Centri di gravità di alcune semplici forme geometriche

Per determinare i centri di gravità di corpi di forma comune (triangolo, arco di cerchio, settore, segmento), è conveniente utilizzare i dati di riferimento (Tabella 6.1).

Tabella 6.1

Coordinate del baricentro di alcuni corpi omogenei

№	Nome della figura	Immagine
	arco di cerchio: il baricentro di un arco di circonferenza omogenea è sull'asse di simmetria (coordinata yc=0). Rè il raggio del cerchio.
	Settore circolare omogeneo yc=0). dove α è la metà dell'angolo centrale; Rè il raggio del cerchio.
	Segmento: il baricentro si trova sull'asse di simmetria (coordinata yc=0). dove α è la metà dell'angolo centrale; Rè il raggio del cerchio.
	Semicerchio:
	Triangolo: il baricentro di un triangolo omogeneo si trova nel punto di intersezione delle sue mediane. dove x1 , y1 , x2 , y2 , x3 , y3- coordinate dei vertici del triangolo
	Cono: il baricentro di un cono circolare omogeneo giace alla sua altezza ed è ad una distanza di 1/4 dell'altezza dalla base del cono.