Răspunsul este traiectoria punctului B - astroid s t)
Curbele cicloide includ nu numai cicloid, epi- și hipocicloid, ci și trohoid, cardioid, astroid, descrise mai jos.
Coordonatele X, y satisfac în acest caz ecuația astroidă (Fig. 91)
Excepția dă (astroid)
Când p \u003d r \u003d (m \u003d 3), hipocicloidul se numește astroid (Fig. 64), iar ecuațiile iau forma x \u003d R os i y \u003d R sin "i sau x -y \u003d R.
Când p = r = - (m = 3) hipocicloidul se numește astroid (Fig. 64), iar ecuațiile iau forma
Pe fig. 72 segmentul AB = I este fixat pe legătura AB = I la un unghi 0 = 180°. Prin urmare, astroidul desenat de punctul Bi este rotit în raport cu astroidul desenat de punctul B cu un unghi m6,
Să analizăm problema trasării tangentelor la această curbă folosind mecanismul luat în considerare. În conformitate cu regula formulată mai sus, tangenta la astroid va tăia pe linia manivelei OA un segment egal cu numitorul fracției din partea dreaptă a expresiei (160). În ceea ce privește mecanismul prezentat în fig. 72, dimensiunea segmentului de tăiat este determinată de formula (172)
În practică, pentru construcția de astroizi în condiții de producție, fiecare linie dreaptă în care se deplasează
Pe fig. 72 am arătat mecanismul care asigură capetele S și Si ale legăturii 10 cu mișcare de-a lungul a două astroide rotite unul față de celălalt cu 45°.
Curba descrisă de ecuațiile (57) și (58) va fi o curbă de tip astroid. Axele de simetrie ale acestei curbe se formează cu axele Ax
Să afișăm, așa cum se face în , aspectul astroidului pe semiplanul Re5>0
Presupunând a = p = 1, construim un contur în care astroidul a fost deformat (Fig. 24).
Glisoarele / și 2 alunecă în ghidajele fixe p și q, ale căror axe sunt reciproc perpendiculare. Ramurile a și 6 ale glisoarelor 1 până la 2 alunecă într-un glisor cruciform 3, ale cărui axe sunt de asemenea reciproc perpendiculare. Legătura 4 intră în perechea de rotație C cu glisorul 3 și alunecă în glisorul în formă de cruce 5, care alunecă de-a lungul axei verigii 6, care este inclusă în perechile de rotație L și B cu glisoare / și 2. Când glisoarele I la 2 se deplasează de-a lungul ghidajelor iar punctul K descrie un arc astroizi, a cărui ecuație este = unde 1 - AB. În acest caz, linia directă se îndoaie
Hipocicloidul are n - -1 cuspizi, fiecare dintre ele echivalent din punct de vedere al concentrației tensiunii până la capătul fisurii (un astroid cu n = 3 este prezentat în Fig. PZO). Defectele de acest tip pot determina rezistența fragilității
Aflați ecuația tangentei la astroid.
Pe fig. 72 prezintă un mecanism cu zece legături conceput pentru a juca astroizi. Astroidul este un hipocicloid obișnuit cu modul m = și este o curbă algebrică de ordinul 6. Numele astroidului
Astfel, tangenta la unul dintre astroidele prezentate în desen va trece prin punctele C și 5, iar tangenta la celălalt va trece prin punctele C și S. Dar punctele B și B sunt capetele bielei B B ale grup asemănător lambda în linia dreaptă Hart. Prin urmare, capătul B va aluneca întotdeauna de-a lungul legăturii DDj, iar capătul B - de-a lungul perpendicularei restabilite la DDj din punctul C. Rezultă că astroidul desenat de punctul B este anvelopa tuturor pozițiilor legăturii DD. Cele de mai sus pot fi extinse și la astroidele reproduse de punctul B sau de orice punct al cercului circumscris lui A de raza I.
După cum se știe, rădăcina astroidului, dacă centrul de simetrie al acestuia din urmă este ales ca pol, este un trandafir cu patru petale. Astfel, este suficient să lungim segmentele ABi = AB din Fig. 72 (sau în Fig. 73) la dimensiunea AB \u003d ABi \u003d L, pentru a obține cu aceasta
CULTURA ISIORIELOR MECANISMUL IMPORTANT AL VYATKINULUI PENTRU REPRODUCEREA ASTROIDULUI
Pentru a pune capăt lucrării legate direct de teoria aripii, remarcăm lucrarea lui G.N. Babaeva Despre rotoarele lui Flettner (Study of Sarat. State University, Pedagogical Faculty. Vol. VH. Issue 11, 1929), în care autorul aplică metoda obișnuită de studiere a aripilor în cazul a două rotoare Flettner. De altfel, autorul a arătat că șirul momentelor în acest caz este un astroid. Cu privire la
Linie (curba) de ordinul al patrulea numiți o dreaptă definită de o ecuație algebrică de gradul al patrulea în raport cu coordonatele dreptunghiulare carteziene. Liniile (curbele) din ordinea a cincea, a șasea și a altor ordine sunt definite în mod similar.
Setul de linii (curbe) de ordinul al patrulea nu mai conține zeci, ci mii de linii de un anumit tip. Seturile de linii de ordinul al cincilea și al șaselea sunt și mai diverse. Aici luăm în considerare anumite tipuri de linii de ordinul al patrulea și superior, care au proprietăți interesanteși aplicații practice.
Lemniscate Bernoulli
Să ne întoarcem la curba descrisă de punctul M pe plan astfel încât produsul p al distanțelor acestui punct la două puncte specifice F 1 și F 2 ale aceluiași plan să rămână neschimbat. O astfel de curbă se numește lemniscate (lemniscate în greacă înseamnă „panglică”). Dacă lungimea segmentului F 1 F 2 este c, atunci distanțele de la mijlocul O al segmentului F 1 F 2 la F1 și F2 sunt egale cu c / 2 și produsul acestor distanțe este egal cu - c 2 / 4. Să cerem mai întâi ca valoarea lui p a produsului invariabil să fie exact egală cu 2/4; apoi
spirală transcendentă în ordinea liniilor
Orez. 8
punctul O se va întinde pe lemniscate, iar lemniscata în sine va arăta ca un „opt culcat” (Fig. 8). Dacă continuăm segmentul F 1 F 2 în ambele sensuri până la intersecția cu lemniscata, atunci obținem două puncte A 1 și A 2. Exprimăm distanța dintre A 1 A 2 \u003d x printr-o distanță cunoscută c:
Focarele lemniscate sunt F1 (? c; 0) și F2 (c; 0). Luați un punct arbitrar M (x; y). Produsul distanțelor de la focare până la punctul M este
Și prin definiție este egal cu c2:
Punem la patrat ambele laturi ale ecuatiei:
Extindeți parantezele din partea stângă:
Deschidem parantezele și prăbușim noul pătrat al sumei:
Scoatem factorul comun și transferăm:
În acest caz, a este raza cercului care descrie lemniscata. După ce am efectuat transformări simple, putem obține o ecuație explicită:
Îndreptăm și deschidem parantezele:
Ne aducem în minte
Aceasta este ecuație pătratică cu privire la y". Rezolvând-o, obținem
Luând rădăcina și eliminând opțiunea cu un al doilea termen negativ, obținem:
unde varianta pozitivă definește jumătatea superioară a lemniscatei, varianta negativă o definește pe cea inferioară.
Dacă valoarea produsului constant p nu este egală cu 2/4, atunci lemniscata își va schimba forma. Și când p este mai mic decât c 2 /4, lemniscata este formată din două ovale, fiecare dintre ele conținând punctele F 1 și, respectiv, F 2 (Fig. 9).

Orez. 9
Acea. prin stabilirea unor condiţii diferite pentru p şi c 2 /4 vom obţine lemniscate de diferite tipuri (Fig. 10).

Orez. 10
Să luăm acum orice număr de puncte din avion. F 1 , F 2 ,…, F n Să obținem o curbă, a cărei formă va depinde de modul în care punctele F 1 , F 2 ,…, F n sunt situate unul față de celălalt și care este valoarea produsului constant. Această curbă se numește lemniscat cu n focare.
Mai sus, am considerat lemniscate cu două focare. Luând un număr diferit de focare, aranjandu-le în moduri diferite și atribuind cutare sau cutare valoare produsului distanțelor, se pot obține lemniscate de contururi cele mai bizare. Să conducem punctul creionului dintr-un anumit punct A, fără să-l scoatem de pe hârtie, astfel încât să revină în cele din urmă la punctul de plecare A. Apoi va descrie o anumită curbă; cerem doar ca această curbă să nu se intersecteze nicăieri

Orez. 11
în sine. Evident, în acest fel se pot obține curbe, având, de exemplu, contururile unui cap de om sau ale unei păsări (Fig. 11). Se dovedește că, având o astfel de curbă arbitrară, se poate alege numărul n și dispunerea focarelor în așa fel
F 1 , F 2 ,…, F n
și atribuiți o astfel de valoare pentru un produs constant al distanțelor
МF 1 МF 2 … МF n = p
că lemniscata corespunzătoare prin ochi nu va diferi de această curbă. Cu alte cuvinte, posibilele abateri ale punctului M, care descrie lemniscata, de la curba desenată - nu vor depăși lățimea trazei creionului (creionul poate fi ascuțit în prealabil așa cum doriți, astfel încât cursa să fie foarte îngust). Acest fapt remarcabil, care vorbește despre extraordinara diversitate și bogăție a formelor lemniscatelor cu multe focare, este dovedit destul de riguros, dar foarte greu, cu ajutorul matematicii superioare.
melcul lui Pascal

Locul punctelor M și M" situat pe liniile creionului (al cărui centru O se află pe un cerc cu raza R) la distanța a de ambele părți ale punctului P de intersecție a liniilor cu cercul; astfel, PM = PM" = a. ecuație în coordonate dreptunghiulare: (x2 + y2 - 2Rx)2 - a2(x2 + y2) = 0, în coordonate polare: r = 2R cos j + a. Când a = 2R, bucla se contractă până la un punct, caz în care cohleea lui Pascal se transformă într-un cardioid. Numele este numit după omul de știință francez B. Pascal (1588-1651), care l-a studiat pentru prima dată.
Curbe cicloide
Imaginează-ți că o anumită curbă se rostogolește fără să alunece de-a lungul unei alte curbe; orice punct, asociat invariabil cu prima curbă, va descrie o nouă curbă. Așa că vă puteți imagina o elipsă care se rostogolește pe o altă elipsă și să explorați linia de-a lungul căreia se va mișca centrul ei sau să determinați traiectoria focarului unei parabole care se rostogolește în linie dreaptă și așa mai departe.
Dintre curbele astfel formate se disting curbele care sunt traiectoriile unui punct legat invariabil de un cerc care se rostogoleste fara sa alunece de-a lungul altui cerc. Liniile rezultate sunt numite cicloidal.
Când se formează curbele cicloidale, punctul de trasare este separat de centrul cercului generator (în mișcare) la o anumită distanță. Într-un caz particular, este pe circumferința cercului generator. În această condiție, curbele rezultate se împart în epicicloizi și hipocicloizi, în funcție de situația cercul generator în exterior sau în interiorul cercului fix.
Curbele algebrice includ curbe binecunoscute precum cardioid, astroid, să luăm în considerare aceste curbe.
Cardioid
1. Ecuația. Un cardioid poate fi definit ca traiectoria unui punct situat pe circumferința unui cerc cu raza r care se rostogolește de-a lungul circumferinței unui cerc staționar de aceeași rază. Va fi astfel un epicicloid cu modul m egal cu 1.
Această împrejurare face posibilă notarea imediată a ecuațiilor parametrice ale cardioidului, înlocuind modulul m cu unul în ecuațiile parametrice de mai sus ale epicicloidului. Vom avea:
Pentru a obține ecuația polară a cardioidului, este convenabil să luați punctul A drept pol (Fig. 13) și să direcționați axa polară de-a lungul abscisei. Întrucât patrulaterul AOO 1 M va fi un trapez isoscel, atunci unghiul polar al punctului M va fi egal cu unghiul de rotație al cercului generator, adică. parametrul t. Având în vedere această împrejurare, să înlocuim y în a doua ecuație a sistemului (1) prin sin t. Reducand egalitatea astfel obtinuta prin sin t se obtine ecuatia polara a cardioidului

Orez. 13
Conform acestei ecuaţii
putem concluziona că cardioidul este unul dintre melcii lui Pascal. Poate fi definit, așadar, ca concoida unui cerc.
Traducând ecuația (2) într-un sistem de coordonate dreptunghiular, obținem:
Din această ecuație rezultă că cardioidul este o curbă algebrică de ordinul 4.
2. Proprietăți. În primul rând, deoarece cardioidul este un epicicloid cu m=1, îi pot fi transferate toate proprietățile epicicloizilor considerați în paragraful anterior.
Iată caracteristicile și specificațiile.
1. Tangenta într-un punct arbitrar al cardioidului trece prin punctul cercului cercului generator, diametral opus punctului de contact al cercurilor, iar normala trece prin punctul de contact al acestora.
2. Unghiul format de tangenta la cardioid cu vectorul raza punctului de contact este egal cu jumatate din unghiul format de acest vector raza cu axa polară. Într-adevăr
Din această relație rezultă direct că unghiul format de tangenta la cardioid cu axa absciselor este egal (ca unghiul extern al triunghiului AMN Fig. 14). Având o formulă, putem demonstra că tangentele la cardioid, trasate la capetele coardei care trece prin pol, sunt reciproc perpendiculare.
Într-adevăr, din moment ce

Orez. 14
De asemenea, remarcăm că locul punctelor de intersecție ale acestor tangente este un cerc.Într-adevăr, ecuația primei tangente, bazată pe ecuațiile (1) ale cardioidului, va avea forma
iar tangenta a doua Eliminand parametrul din aceste ecuatii, obtinem ecuatia cercului indicat.
3. Raza de curbură într-un punct arbitrar al cardioidului este determinată de formula
De asemenea, se poate demonstra că raza de curbură este 2/3 din normala polară N într-un punct dat.
Într-adevăr, de unde pe baza (4) obținem.Această relație poate fi folosită pentru a construi centrul de curbură al cardioidului.
4. Evolutia unui cardioid, dupa proprietatea generala a evolutiei unui epicicloid, va fi si un cardioid asemanator celui dat, cu un coeficient de asemanare egal cu 1/3, si rotit fata de cel dat de o unghi de 180°.
5. Lungimea arcului cardioid de la punctul A la un punct arbitrar M este determinată de formula
Dacă lungimea arcului se numără din punctul A 1, diametral opus punctului A, atunci formula pentru determinarea lungimii arcului poate fi scrisă ca
6. Ecuația naturală a cardioidului se obține dacă parametrul este exclus din egalitățile (4) și (6). Va arata ca
7. Aria delimitată de un cardioid este determinată de formula
și, după cum se poate vedea, este egală cu zona cu șase roți a cercului generator.
Lungimea întregului cardioid este determinată de formulă
și, după cum se poate observa, este egal cu opt diametre ale cercului generator. Volumul corpului obținut din rotația cardioidului în jurul axei sale este egal cu
Suprafața corpului obținută din rotația cardioidului în jurul axei sale este egală cu
Am văzut că cardioidul este legat organic de cercul. Este un conchoid al unui cerc și un epicicloid. Are o relație diferită cu un cerc - un cardioid este o subera a unui cerc în raport cu un punct aparținând acestui cerc.

Orez. 15
Într-adevăr, fie OM perpendiculara coborâtă la tangenta la cercul cu raza egală cu 2r desenată în punctul N.
Deoarece OM \u003d OB + BM sau \u003d\u003d 2r cos + 2r, atunci locul punctelor M va fi un cardioid cu ecuația \u003d 2r (1 + cos)
În concluzie, observăm că cardioidul aparține și familiei spiralelor sinusoidale, iar proprietățile sale individuale se repetă proprietăți generale aceste curbe. Din aceste proprietăți rezultă, în special, că inversarea cardioidului, față de cuspid, dă o parabolă.
Astroid
1. Proprietăți. Astroidul este un caz special de hipocicloizi, și anume, un hipocicloid cu modul m egal cu 1/4. Este, prin urmare, traiectoria unui punct situat pe cercul unui cerc cu raza r, care se rostogolește de-a lungul interiorului altui cerc fix, a cărui rază R este de patru ori mai mare.
Ecuațiile parametrice ale astroidului pot fi obținute punând hipocicloizi în ecuații, m=1/4. Iată ecuațiile:


Orez. 16
unde t, ca mai înainte, este unghiul de rotație al cercului generator (Fig. 16)
Eliminând parametrul t din ecuațiile (1), obținem:
Ecuația (2) implică faptul că astroidul este o curbă algebrică de ordinul al șaselea.
Ecuațiile parametrice (1) ale astroidului pot fi reduse la forma

Eliminând parametrul t din aceste ecuații, obținem forma utilizată frecvent a ecuației astroide
Presupunând în relațiile generale derivate anterior pentru curbele cicloidale modulul
m = -1/4, obținem relațiile corespunzătoare pentru astroid:
1) raza de curbură într-un punct arbitrar al astroidului este determinată de formula
2) lungimea arcului astroidului de la punctul A la un punct arbitrar M(t) este determinată de formula
lungimea unei ramuri este egală cu și lungimea întregii curbe este 6R;
3) pentru a obține ecuația naturală a astroidului, observăm mai întâi că dacă punctul de plecare pentru lungimea arcului nu este punctul A, pentru care t = 0, ci punctul pentru care t = , atunci lungimea arcului arcul este determinat de formula
excluzând parametrul t din ecuațiile (5) și (6), obținem ecuația naturală a astroidului
4) evolutia unui astroid este si un astroid asemanator celui dat, cu un coeficient de asemanare egal cu 2, rotit fata de cel dat printr-un unghi /4 (Fig. 16)
5) aria delimitata de intregul astroid este egala cu volumul corpului obtinut din rotatia astroidului, egal cu 32/105 R 3
suprafaţa corpului formată prin rotaţia astroidului este egală cu
Să ne întoarcem acum la considerarea unor proprietăți particulare ale astroidului.
Astroidul este învelișul unui segment de lungime constantă, capete. care alunecă de-a lungul a două drepte reciproc perpendiculare.
Luăm aceste drepte drept axe de coordonate și, notând unghiul de înclinare al segmentului de alunecare ND=R prin (Fig. 4), vom avea ecuația dreptei ND sub forma
Diferențiând această ecuație față de parametru, obținem:
Eliminand parametrul din ultima ecuatie si ecuatie (7), vom avea ecuatia plic sub forma i.e. astroid.
În practică, mișcarea segmentului ND poate fi efectuată folosind așa-numitele cercuri cardanice. Unul dintre aceste cercuri cu raza R este nemișcat, iar celălalt, cu raza r, de două ori mai mic, se rostogolește de-a lungul părții interioare a cercului nemișcat. Oricare două puncte diametral opuse N și D ale cercului de rulare se vor mișca de-a lungul a două diametre reciproc perpendiculare Ox și Oy ale cercului staționar. Este clar că învelișul cu diametrul cercului de rulare va fi astroidul.
 Orez. 17 |
 Orez. 18 |
Metoda considerată de formare a unui astroid poate fi interpretată și după cum urmează. Dreptunghiul ODCN, ale cărui două laturi se află pe două linii reciproc perpendiculare, este deformat astfel încât diagonala sa păstrează o lungime egală cu R, învelișul diagonalei va fi un astroid. Deoarece în acest caz perpendiculara căzută de la vârful C la diagonala DN servește ca normală la plic, astroidul este locul bazelor perpendicularelor căzute de la vârful C al dreptunghiului la diagonala acestuia.
Pentru , aceste ecuații exprimă astroidul direct considerat mai devreme.
- (din vedere greacă a stelei astron și eidos) o curbă plată descrisă de un punct de cerc care atinge un cerc fix de patru ori mai mare din interior și se rostogolește de-a lungul acestuia fără alunecare. Aparține hipocicloizilor. algebric astroid ...... Mare Dicţionar enciclopedic
Exist., Număr de sinonime: 1 curbă (56) Dicţionar de sinonime ASIS. V.N. Trishin. 2013... Dicţionar de sinonime
- (din vedere greacă a stelei ástron și éidos), o curbă plată descrisă de un punct pe un cerc care atinge un cerc fix de patru ori mai mare din interior și se rostogolește de-a lungul acestuia fără alunecare. Aparține hipocicloizilor. Astroid ...... Dicţionar enciclopedic
- (astro... gr. eidos view) mat. o curbă plată descrisă de un punct al unui cerc care se rostogolește fără alunecare de-a lungul părții interioare a altui cerc fix, cu o rază de patru ori mai mare decât cea a primului; arată ca o stea cu patru colțuri. Dicționar nou … Dicționar de cuvinte străine ale limbii ruse
Algebră plată. curba ti ro a ordinului, până la margine este descrisă de punctul Cercului cu raza r, rostogolindu-se de-a lungul laturii interioare a cercului cu raza R=4r; hipocicloid cu modul r=4. Ecuație în coordonate carteziene: parametrice. ecuatii... Enciclopedie matematică
O curbă sau o linie este un concept geometric care este definit diferit în diferite secțiuni.
CURVĂ (linie), o urmă lăsată de un punct sau de un corp în mișcare. De obicei, o curbă este reprezentată doar ca o linie curbă netedă, ca o parabolă sau un cerc. Dar conceptul matematic al unei curbe acoperă atât o linie dreaptă, cât și figuri formate din segmente de linie, cum ar fi un triunghi sau un pătrat.
Curbele pot fi împărțite în plane și spațiale. O curbă plană, cum ar fi o parabolă sau o linie dreaptă, se formează la intersecția a două plane sau a unui plan și a unui corp și, prin urmare, se află în întregime într-un singur plan. O curbă spațială, de exemplu, o spirală în formă de arc elicoidal, nu poate fi obținută ca intersecție a oricărei suprafețe sau corp cu un plan și nu se află într-un singur plan. Curbele pot fi, de asemenea, împărțite în închise și deschise. O curbă închisă, cum ar fi un pătrat sau un cerc, nu are capete, adică punctul în mișcare care generează o astfel de curbă își repetă periodic traseul.
O curbă este un loc, sau o mulțime, de puncte care satisfac o anumită condiție sau ecuație matematică.
De exemplu, un cerc este locul punctelor dintr-un plan care sunt echidistante de un punct dat. Curbe definite ecuații algebrice, se numesc curbe algebrice.
De exemplu, ecuația unei drepte y = mx + b, unde m este panta și b este segmentul tăiat pe axa y, este algebrică.
Curbe ale căror ecuații conțin funcții transcendentale, cum ar fi logaritmii sau funcții trigonometrice, se numesc curbe transcendentale.
De exemplu, y = log x și y = tg x sunt ecuații ale curbelor transcendentale.
Forma unei curbe algebrice poate fi determinată de gradul ecuației sale, care coincide cu cel mai înalt grad al termenilor ecuației.
Dacă ecuația de gradul întâi, de exemplu Ax + By + C = 0, atunci curba are forma unei linii drepte.
Dacă o ecuație de gradul doi, de exemplu,
Ax 2 + By + C = 0 sau Ax 2 + By 2 + C = 0, atunci curba este pătratică, adică. reprezintă una dintre secțiunile conice; astfel de curbe includ parabole, hiperbole, elipse și cercuri.
Enumerăm formele generale ale ecuațiilor secțiunilor conice:
x 2 + y 2 \u003d r 2 - cerc,
x 2 / a 2 + y 2 / b 2 \u003d 1 - elipsă,
y \u003d axa 2 - parabolă,
x 2 / a 2 - y 2 / b 2 \u003d 1 - hiperbolă.
Curbele corespunzătoare ecuațiilor a treia, a patra, a cincea, a șasea etc. gradele se numesc curbe ale treilea, al patrulea, al cincilea, al șaselea etc. Ordin. În general, cu cât gradul ecuației este mai mare, cu atât mai multe curbe va avea o curbă deschisă.
Multe curbe complexe au primit denumiri speciale.
O cicloidă este o curbă plană descrisă de un punct fix al unui cerc care se rostogolește de-a lungul unei linii drepte, numită generatoarea cicloidei; o cicloidă este formată dintr-o serie de arce care se repetă.
Un epicicloid este o curbă plană descrisă de un punct fix pe un cerc care se rostogolește de-a lungul altui cerc fix în afara acestuia.
Un hipocicloid este o curbă plană descrisă de un punct fix al unui cerc care se rostogolește din interior de-a lungul unui cerc fix.
O spirală este o curbă plată care se desfășoară o tură după alta dintr-un punct fix (sau se înfășoară în jurul lui).
Matematicienii au studiat proprietățile curbelor din cele mai vechi timpuri, iar numele multor curbe neobișnuite sunt asociate cu numele celor care le-au studiat pentru prima dată. Astfel sunt, de exemplu, spirala lui Arhimede, bucla lui Agnesi, cisoida lui Diocles, cocoida lui Nicomede și lemniscata lui Bernoulli.
În cadrul geometriei elementare, conceptul de curbă nu primește o formulare distinctă și este uneori definit ca „lungime fără lățime” sau ca „limită a unei figuri”. În esență, în geometria elementară, studiul curbelor se reduce la a lua în considerare exemple (, , , si etc.). Lipsită de metode generale, geometria elementară a pătruns destul de adânc în studiul proprietăților curbelor specifice (, nisteSi deasemenea), folosind tehnici speciale în fiecare caz.
Cel mai adesea, o curbă este definită ca o mapare continuă de la un segment la:
În acest caz, curbele pot fi diferite, chiar dacă acesteaMeci. Astfel de curbe se numesccurbe parametrizatesau daca[ A , b ] = , moduri.
Uneori, curba este definită până la , adică până la relația de echivalență minimă astfel încât curbele parametrice
sunt echivalente dacă există o continuă (uneori nedescrescătoare) h din segmentul [ A 1 ,b 1] în segmentul [ A 2 ,b 2], astfel încât
![]()
Cele determinate de această relație se numesc sau pur și simplu curbe.
Definiții analitice
În cursurile de geometrie analitică se demonstrează că printre liniile scrise în coordonate dreptunghiulare carteziene (sau chiar în general afine) ecuație generală gradul doi
Ax 2 + 2Bxy + Cy 2 + 2Dx + 2Ey + F = 0
(unde cel puțin unul dintre coeficienții A, B, C este diferit de zero) există doar următoarele opt tipuri de linii:
a) o elipsă;
b) hiperbola;
c) parabola (curbe nedegenerate de ordinul doi);
d) o pereche de drepte care se intersectează;
e) o pereche de drepte paralele;
f) o pereche de linii coincidente (o linie);
g) un punct (linii degenerate de ordinul doi);
h) o „linie” care nu conține deloc puncte.
Dimpotrivă, orice linie din fiecare dintre aceste opt tipuri este scrisă în coordonate dreptunghiulare carteziene printr-o ecuație de ordinul doi. (În cursurile de geometrie analitică, se vorbește de obicei despre nouă (nu opt) tipuri de secțiuni conice, deoarece ele disting între o „elipsă imaginară” și o „pereche de linii paralele imaginare” - geometric aceste „linii” sunt aceleași, deoarece ambele nu conțin un singur punct, dar analitic sunt scrise prin ecuații diferite.) Prin urmare, secțiunile conice (degenerate și nedegenerate) pot fi definite și ca drepte de ordinul doi.
LAo curbă într-un plan este definită ca un set de puncte ale căror coordonate satisfac ecuațiaF ( X , y ) = 0 . În același timp, pentru funcțieF se impun restricţii care garantează că această ecuaţie are un număr infinit de soluţii necoincidente şi
acest set de soluții nu umple „bucata de avion”.
Curbe algebrice
O clasă importantă de curbe sunt cele pentru care funcțiaF ( X , y ) existădin două variabile. În acest caz, curba definită de ecuațieF ( X , y ) = 0 , se numește.
Curbele algebrice date de ecuația de gradul I sunt .
O ecuație de gradul 2, care are un număr infinit de soluții, determină, adică degenerată și nedegenerată.
Exemple de curbe date prin ecuații de gradul 3: , .
Exemple de curbe de gradul 4: și .
Un exemplu de curbă de gradul 6: .
Un exemplu de curbă definită printr-o ecuație de putere pară: (multifocal).
Curbe algebrice definite prin ecuații grade superioare, sunt considerate în . În același timp, teoria lor capătă o armonie mai mare dacă luarea în considerare este efectuată pe . În acest caz, curba algebrică este determinată de o ecuație de formă
F ( z 1 , z 2 , z 3 ) = 0 ,
Unde F este un polinom de trei variabile care sunt puncte.
Tipuri de curbe
O curbă plană este o curbă ale cărei puncte se află în același plan.
(o linie simplă sau un arc iordanian, de asemenea un contur) este un set de puncte dintr-un plan sau spațiu care sunt în corespondență unu-la-unu și reciproc continuă cu segmentele de linie.
Calea - segment în .
curbe analitice care nu sunt algebrice. Mai exact, curbe care pot fi definite prin linia de nivel a unei funcții analitice (sau, în cazul multidimensional, a unui sistem de funcții).
sinusoid,
Cicloid,
Spirala lui Arhimede
tractor,
linie de lanț,
Spirala hiperbolica etc.
Modalități de definire a curbelor:
analitic - curba este dată de o ecuație matematică;
grafic - curba este setată vizual pe purtătorul de informații grafice;
tabulară - curba este dată de coordonatele unei serii de puncte.
parametrică (cel mai general mod de a specifica ecuația unei curbe):
Unde - funcții netede ale parametrilort, și
(X") 2 + (y") 2 + (z") 2 > 0 (condiția de regularitate).
Este adesea convenabil să folosiți notația invariantă și compactă a ecuației curbei cu:
unde în partea stângă sunt puncte ale curbei, iar partea dreaptă determină dependența acesteia de un parametru t. Expandând această notație în coordonate, obținem formula (1).
Cicloid.
Istoria studiului cicloidului este asociată cu numele unor astfel de mari oameni de știință, filozofi, matematicieni și fizicieni precum Aristotel, Ptolemeu, Galileo, Huygens, Torricelli și alții.
Cicloid(dinκυκλοειδής - rotundă) - care poate fi definită ca traiectoria unui punct situat la limita unui cerc care se rostogolește fără alunecare în linie dreaptă. Acest cerc se numește cerc generator.
Una dintre cele mai vechi moduri de formare a curbelor este metoda cinematică, în care curba se obține ca traiectorie a unui punct. Curba, care se obține ca traiectorie a unui punct fixat pe un cerc, care se rostogolește fără alunecare de-a lungul unei linii drepte, de-a lungul unui cerc sau a unei alte curbe, se numește cicloidă, care se traduce din greacăînseamnă circular, care amintește de un cerc.
Să luăm mai întâi în considerare cazul când cercul se rostogolește de-a lungul unei linii drepte. O curbă descrisă de un punct fixat pe un cerc care se rostogolește fără alunecare în linie dreaptă se numește cicloidă.
Lasă un cerc cu raza R să se rotească de-a lungul unei drepte a. C este un punct fixat pe un cerc, în momentul inițial al timpului aflându-se în poziția A (Fig. 1). Să punem pe o dreaptă un segment AB, egal cu circumferința cercului, adică. AB \u003d 2 π R. Împărțim acest segment în 8 părți egale prin punctele A1, A2, ..., A8 \u003d B.

Este clar că atunci când cercul, rostogolindu-se de-a lungul liniei drepte a, face o revoluție, adică. se rotește la 360, apoi va lua poziția (8), iar punctul C se va muta din poziția A în poziția B.
Dacă cercul face o jumătate de tură completă, de exemplu. se rotește cu 180, apoi va ocupa poziția (4), iar punctul C se va muta în cea mai înaltă poziție C4.
Dacă cercul este rotit cu un unghi de 45, atunci cercul se va muta în poziția (1), iar punctul C se va muta în poziția C1.
Figura 1 prezintă, de asemenea, alte puncte ale cicloidului corespunzătoare unghiurilor de rotație rămase ale cercului, care sunt multipli de 45.
Conectând punctele construite cu o curbă netedă, obținem o secțiune a cicloidă corespunzătoare unei revoluții complete a cercului. Odată cu următoarele revoluții se vor obține aceleași secțiuni, adică. cicloidul va consta dintr-o secțiune care se repetă periodic numită arc cicloid.
Să fim atenți la poziția tangentei la cicloidă (Fig. 2). Dacă ciclistul merge pe un drum umed, atunci picăturile rupte de pe roată vor zbura tangențial la cicloid și, în absența scuturilor, pot împroșca spatele biciclistului.

Prima persoană care a studiat cicloidul a fost Galileo Galilei (1564-1642). El a venit și cu numele lui.
Proprietățile cicloidului:
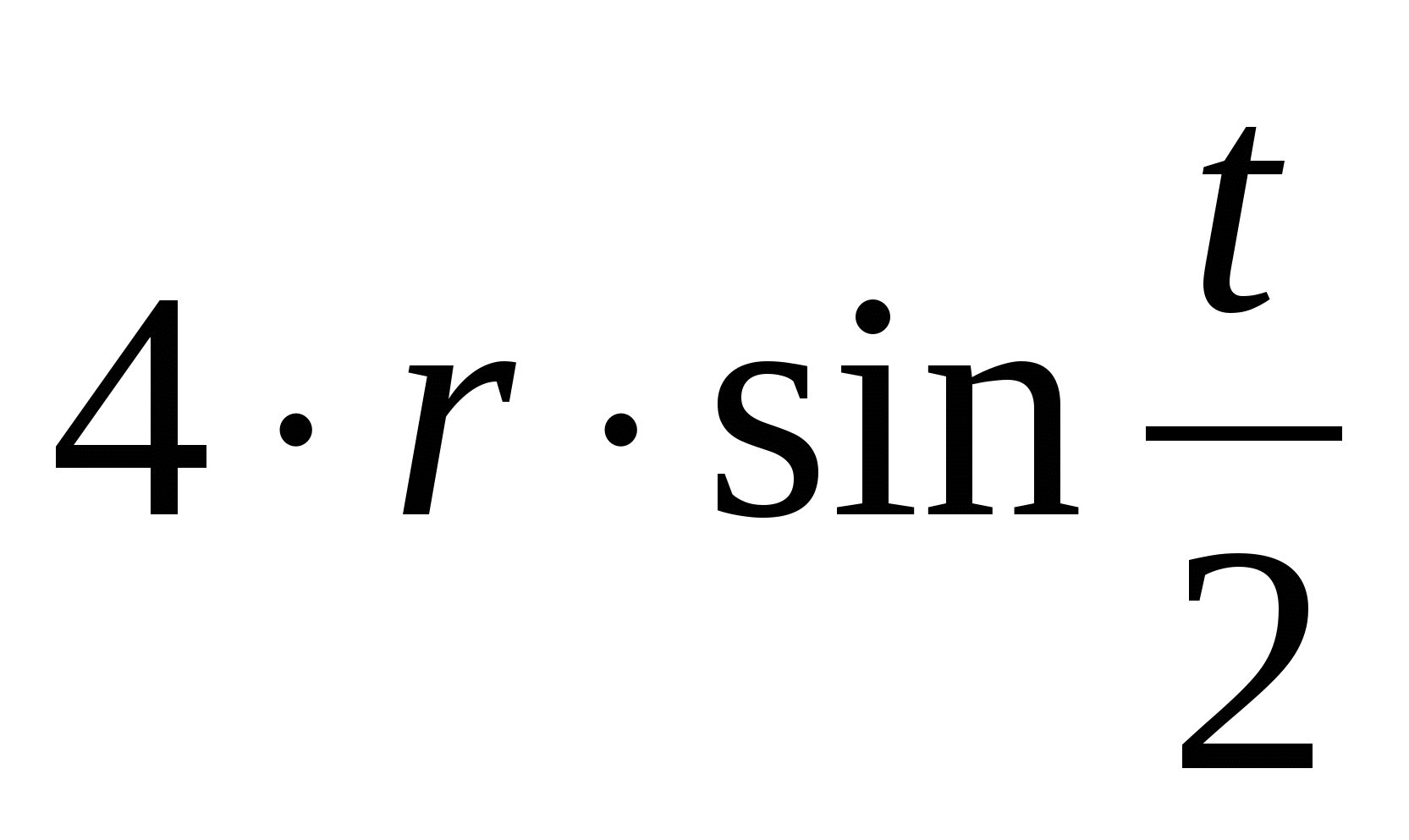
Cicloidul are o serie de proprietăți remarcabile. Să menționăm câteva dintre ele.
Proprietatea 1. (Munte de gheață.) În 1696, I. Bernoulli a stabilit sarcina de a găsi cea mai abruptă curbă de coborâre, sau, cu alte cuvinte, problema a ceea ce ar trebui să fie forma unui deal de gheață pentru a face o cale din punct de startȘi până la punctul final B în cel mai scurt timp (Fig. 3, a). Curba dorită a fost numită „brahistocron”, adică. cea mai scurtă curbă de timp.

Este clar că cea mai scurtă cale de la punctul A la punctul B este segmentul AB. Totuși, cu așa ceva mișcare rectilinie viteza crește încet și timpul petrecut la coborâre se dovedește a fi mare (Fig. 3, b).
Viteza se câștigă cu cât mai repede, cu atât coborârea este mai abruptă. Cu toate acestea, cu o coborâre abruptă, traseul de-a lungul curbei este prelungit și, prin urmare, timpul de trecere a acesteia crește.
Printre matematicienii care au rezolvat această problemă s-au numărat: G. Leibniz, I. Newton, G. Lopital și J. Bernoulli. Ei au demonstrat că curba dorită este o cicloidă inversată (Fig. 3, a). Metodele dezvoltate de acești oameni de știință în rezolvarea problemei brahistocronului au pus bazele unei noi direcții în matematică - calculul variațiilor.
Proprietatea 2. (Ceasuri cu pendul.) Un ceas cu pendul obișnuit nu poate funcționa cu precizie, deoarece perioada de oscilație a pendulului depinde de amplitudinea acestuia: cu cât amplitudinea este mai mare, cu atât perioada este mai lungă. Omul de știință olandez Christian Huygens (1629 - 1695) s-a întrebat ce curbă trebuie să urmeze bila de pe șirul pendulului pentru ca perioada de oscilație a acesteia să nu depindă de amplitudine. Rețineți că într-un pendul obișnuit, curba de-a lungul căreia se mișcă mingea este un cerc (Fig. 4).

Curba dorită s-a dovedit a fi o cicloidă inversată. Dacă, de exemplu, se face un jgheab sub forma unui cicloid inversat și o minge este trecută de-a lungul ei, atunci perioada de mișcare a mingii sub acțiunea gravitației nu va depinde de poziția și amplitudinea sa inițială (Fig. 5) . Pentru această proprietate, cicloidul este numit și „tautocron” - o curbă de timpi egali.
Huygens a realizat două scânduri de lemn cu margini în formă de cicloid, limitând mișcarea firului la stânga și la dreapta (Fig. 6). În acest caz, mingea în sine se va deplasa de-a lungul unui cicloid inversat și, astfel, perioada oscilațiilor sale nu va depinde de amplitudine.
Din această proprietate a cicloidului, în special, rezultă că indiferent din ce loc al alunecării de gheață sub forma unui cicloid inversat începem coborârea, vom petrece același timp până la punctul final.
Ecuația cicloidă
1. Este convenabil să scrieți ecuația cicloidă în termeni de α - unghiul de rotație al cercului, exprimat în radiani, rețineți că α este egal cu drumul parcurs de cercul generator în linie dreaptă.
x=ra– r păcat α
y=r - r cos α
2. Să luăm axa de coordonate orizontală ca o linie dreaptă de-a lungul căreia se rotește cercul generator al razei r.
Cicloidul este descris ecuații parametrice
X = rt – r păcat t,
y = r – r cos t.
Ecuația în:
Cicloidul poate fi obținut ca soluție ecuație diferențială:

Din povestea cicloidului
Primul dintre oamenii de știință a atras atenția asupra cicloidăîn, dar un studiu serios al acestei curbe a început abia în.
Primul care a început să studieze cicloidul a fost Galileo Galilei (1564-1642) - celebrul astronom, fizician și educator italian. El a inventat și numele de „cicloid”, care înseamnă: „amintește de un cerc”. Galileo însuși nu a scris nimic despre cicloidă, dar lucrările sale în această direcție sunt menționate de studenții și adepții lui Galileo: Viviani, Toricelli și alții. Toricelli, un fizician celebru, inventatorul barometrului, a dedicat mult timp matematicii. În Renaștere, nu existau oameni de știință îngusti de specialitate. O persoană talentată era angajată în filozofie, fizică și matematică și peste tot a obținut rezultate interesante și a făcut descoperiri majore. Puțin mai târziu decât italienii, francezii au preluat cicloidul, numind-o „rula” sau „trochoid”. În 1634, Roberval - inventatorul binecunoscutului sistem de greutăți al sistemului de greutăți - a calculat aria delimitată de arcul cicloidului și baza acestuia. Un studiu semnificativ al cicloidă a fost efectuat de un contemporan cu Galileo. Printre , adică curbe a căror ecuație nu poate fi scrisă sub formă de X , y, cicloidul este primul dintre cei studiati.
A scris despre cicloidă:
Ruleta este o linie atât de comună încât după linie dreaptă și cerc nu mai există o linie comună; este desenat atât de des în fața ochilor tuturor, încât trebuie să fii surprins că anticii nu l-au luat în considerare... căci nu este altceva decât o cale descrisă în aer de un cui de roată.
Noua curbă a câștigat rapid popularitate și a fost supusă unei analize aprofundate, care a inclus, , Newton,, frații Bernoulli și alți luminari ai științei din secolele XVII-XVIII. Pe cicloidă, metodele apărute în acei ani. Faptul că studiul analitic al cicloidei s-a dovedit a fi la fel de reușit ca și analiza curbelor algebrice a făcut o mare impresie și a devenit un argument important în favoarea „egalizării drepturilor” curbelor algebrice și transcendentale. Epicicloid
Unele tipuri de cicloizi

Epicicloid - traiectoria punctului A, culcat pe un cerc cu diametrul D, care se rostogoleste fara sa alunece de-a lungul unui cerc de ghidare de raza R (atingere externa).
Construcția epicicloidului se realizează în următoarea secvență:
Din centrul 0 se trasează un arc auxiliar cu raza egală cu 000=R+r;
Din punctele 01, 02, ... 012, ca din centre, se trasează cercuri cu raza r până se intersectează cu arce auxiliare în punctele A1, A2, ... A12, care aparțin epicicloidului.
 Hipocicloid
Hipocicloid
Hipocicloid - traiectoria punctului A, situat pe un cerc cu diametrul D, care se rostogolește fără alunecare de-a lungul unui cerc de ghidare cu raza R (atingere internă).
Construcția hipocicloidului se realizează în următoarea secvență:
Cercul generator de raza r și cercul de ghidare de raza R sunt desenate astfel încât să se atingă în punctul A;
Cercul generator se împarte în 12 părți egale, se obțin punctele 1, 2, ... 12;
Din centrul 0 se trasează un arc auxiliar cu raza egală cu 000=R-r;
Unghiul central a este determinat de formula a \u003d 360r / R.
Împărțiți arcul cercului de ghidare, limitat de unghiul a, în 12 părți egale, obțineți punctele 11, 21, ... 121;
Din centrul 0 până la punctele 11, 21, ... 121 de linii drepte sunt trasate până la intersecția cu arcul auxiliar în punctele 01, 02, ... 012;
Din centrul 0 se trasează arce auxiliare prin punctele de împărțire 1, 2, ... 12 ale cercului generator;
Din punctele 01, 02, ... 012, ca din centre, se trasează cercuri cu raza r până se intersectează cu arce auxiliare în punctele A1, A2, ... A12, care aparțin hipocicloidului.
Cardioid.
Cardioid ( καρδία - o inima, Cardioid este un caz special Termenul „cardioid” a fost introdus de Castillon în 1741.
Dacă luăm un cerc și un punct pe el ca pol, atunci obținem un cardioid doar dacă lăsăm deoparte segmente egale cu diametrul cercului. Pentru alte valori ale segmentelor trasate, concoidele vor fi cardioide alungite sau scurtate. Acești cardioizi alungiți și scurtați se numesc altfel melcii lui Pascal.
Cardioid are aplicatii diverseîn tehnologie. Sub formă de cardioid, fac excentrici, came pentru mașini. Este folosit uneori la desenarea roților. În plus, este folosit în tehnologia optică.
Proprietățile unui cardioid
cardioid -În M pe un cerc în mișcare va descrie o traiectorie închisă. Această curbă plată se numește cardioid.
2) Cardioid poate fi obținut în alt mod. Marcați un punct pe cerc Oși trageți o grindă din ea. Dacă dintr-un punct DAR intersecția acestei raze cu un cerc, amânați segmentul A.M, de-a lungul lungimii egale cu diametrul cercului și rotiți fasciculul în jurul punctului O, apoi punctul M se va deplasa de-a lungul cardioidului.

3) Un cardioid poate fi reprezentat și ca o curbă tangentă la toate cercurile centrate pe cercul dat și care trec prin punctul său fix. Când sunt construite mai multe cercuri, cardioidul se dovedește a fi construit ca de la sine.

4) Există un alt mod la fel de elegant pe atât de neașteptat de a vedea cardioidul. În figură, puteți vedea o sursă de lumină punctuală pe un cerc. După ce razele de lumină sunt reflectate pentru prima dată din cerc, ele devin tangente la cardioid. Imaginează-ți acum că cercul este marginile cupei, la un moment dat reflectă un bec strălucitor. Cafeaua neagră este turnată în ceașcă, permițându-vă să vedeți razele strălucitoare reflectate. Ca urmare, cardioidul este evidențiat de razele de lumină. 
Astroid.
Astroid (din grecescul astron - stea și eidos - vedere), o curbă plată descrisă de un punct pe un cerc care atinge interiorul unui cerc fix de patru ori mai mare decât raza și se rostogolește de-a lungul acestuia fără alunecare. Aparține hipocicloizilor. Astroid - curbă algebrică de ordinul al 6-lea.
 Astroid.
Astroid. Lungimea întregului astroid este egală cu șase raze ale cercului fix, iar aria delimitată de acesta este trei optimi din cercul fix.
Segmentul tangentei la astroid, cuprins între două raze reciproc perpendiculare ale cercului fix, desenate în vârful astroidului, este egal cu raza cercului fix, indiferent de modul în care a fost ales punctul.
proprietăți astroide
Sunt patruvârf .
Lungimea arcului de la punctul 0 la plic
familii de segmente de lungime constantă, ale căror capete sunt situate pe două linii reciproc perpendiculare.Astroidul este de ordinul 6.
Ecuații astroide
Ecuația în coordonate dreptunghiulare carteziene este:| x | 2 / 3 + | y | 2/3 = R2/3ecuație parametrică:x = Rcos 3 t y = Rsin 3 tCum să construiești un astroid
Desenăm două linii drepte reciproc perpendiculare și desenăm o serie de segmente cu o lungimeR ale căror puncte finale se află pe aceste linii. Figura prezintă 12 astfel de segmente (inclusiv segmentele liniilor reciproc perpendiculare). Cu cât desenăm mai multe segmente, cu atât curba va fi mai precisă. Să construim acum anvelopa tuturor acestor segmente. Acest plic va fi astroidul.

Concluzie
Lucrarea oferă exemple de probleme cu diferite tipuri de curbe, definite prin diferite ecuații sau care satisfac anumite condiții matematice. În special, curbele cicloidale, moduri de a le defini, diferite căi construcții, proprietăți ale acestor curbe.
Proprietățile curbelor cicloidale sunt foarte des folosite în mecanica angrenajelor, ceea ce crește semnificativ rezistența pieselor din mecanisme.