A karakterisztikus egyenletet kapcsolás után állítjuk össze az áramkörre. A következő módokon szerezhető be:

• közvetlenül egy (2) alakú differenciálegyenlet alapján (lásd 24. sz. előadás), i.e. az első és második Kirchhoff-törvény alapján az áramkör elektromágneses állapotát leíró egyenletrendszerből kizárva minden ismeretlen mennyiséget, kivéve egyet, amelyre a (2) egyenletet írják;
• az áramkör bemeneti ellenállásának kifejezést használva szinuszos áramon;
• a fő meghatározó kifejezése alapján.

Az elsõ módszer szerint az elõzõ elõadásban egy soros R-L-C áramkörhöz a kondenzátor feszültségére differenciálegyenletet kaptunk, amely alapján felírjuk a karakterisztikus egyenletet.

Meg kell jegyezni, hogy mivel a lineáris áramkört egyetlen tranziens folyamat fedi le, a gyökerek karakterisztikus egyenlet közösek az áramköri ágak feszültségeinek és áramainak minden szabad összetevőjére, amelyek paramétereit a karakterisztikus egyenlet tartalmazza. Ezért a karakterisztikus egyenlet összeállításának első módszere szerint bármelyiket választható változónak, amelyhez viszonyítva írjuk.

A második és harmadik módszer alkalmazását a karakterisztikus egyenlet összeállítására az 1. ábrán látható áramkör példáján keresztül fogjuk megvizsgálni. egy.

A karakterisztikus egyenlet összeállítása a bemeneti ellenállás módszer szerint a következő:

az áramkör váltóáramú bemeneti impedanciája rögzítésre kerül;

jw helyébe a p operátor lép;

az eredményül kapott kifejezést nullára állítjuk.

Az egyenlet

megfelel a jellemzőnek.

Hangsúlyozni kell, hogy a bemeneti ellenállás az áramkör bármely ágának töréspontjához viszonyítva írható fel. Ebben az esetben az aktív kétterminális hálózatot passzívra cseréljük, az ekvivalens generátor módszeréhez hasonlóan. Ez a módszer a karakterisztikus egyenlet összeállítása magában foglalja a mágnesesen csatolt ágak hiányát az áramkörben; ha vannak, akkor ezek előzetes leválasztását szükséges elvégezni.

ábra szerinti áramkörhöz. 1 a forráskapcsok tekintetében

.

A jw-t p-re cserélve és a kapott kifejezést nullával egyenlővé tesszük, írjuk

.

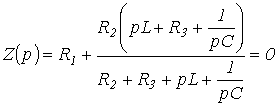
(1)

A fődetermináns kifejezése alapján karakterisztikus egyenlet összeállításánál a felírás alapjául szolgáló algebrai egyenletek száma megegyezik az ismeretlen szabadáram-összetevők számával. Az eredeti integro-rendszer algebraizálása differenciál egyenletek, amelyet például a Kirchhoff-törvények alapján vagy hurokáramok módszerével állítunk össze, úgy hajtjuk végre, hogy a differenciálás és az integráció szimbólumait a p operátorral való szorzással és osztással helyettesítjük. A karakterisztikus egyenletet úgy kapjuk meg, hogy az írott determinánst nullával egyenlővé tesszük. Mivel a fődetermináns kifejezése nem függ az inhomogén egyenletrendszer megfelelő részeitől, ezért összeállítható egy összáramokra felírt egyenletrendszer alapján.

ábra szerinti áramkörhöz. 1, a hurokáramok módszerén alapuló algebraizált egyenletrendszer alakja

Innen származik a rendszer fő meghatározójának kifejezése

D-t nullával egyenlővé téve az (1)-hez hasonló eredményt kapunk.

A tranziensek klasszikus módszerrel történő kiszámításának általános módszertana

Általános esetben a tranziens folyamatok klasszikus módszerrel történő kiszámításának módszere a következő lépéseket tartalmazza:

Példák tranziens folyamatok számítására klasszikus módszerrel

1. Átmeneti folyamatok be R-L láncok feszültségforráshoz csatlakoztatva

Ilyen folyamatok mennek végbe például akkor, ha egy áramforráshoz elektromágneseket, transzformátorokat, villanymotorokat stb.

Tekintsünk két esetet:

ábra szerinti áramkör áramára vonatkozó vizsgált módszer szerint. 2 írható

Karakterisztikus egyenlet

honnan és időállandó .

És így,

.

(5)

A (4)-et és (5)-et a (3) relációba behelyettesítve írjuk

.

Az első kommutációs törvénynek megfelelően. Azután

,

Így a tranziens folyamatban az áramkör áramát az egyenlet írja le

,

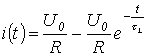és az induktor feszültsége - a kifejezéssel

.

A görbék és a kapott megoldásoknak megfelelő minőségi formáját a ábra mutatja. 3.

A második típusú forrásnál a kényszerített komponens kiszámítása szimbolikus módszerrel történik:

,

A szabad komponens kifejezése nem függ a feszültségforrás típusától. Ennélfogva,

.

Azóta

Így végre megkapjuk

.

(6)

A kapott kifejezés (6) elemzése a következőket mutatja:

Ha nagyságrendileg jelentős, akkor a szabad komponens fél periódus alatt nem csökken jelentősen. Ebben az esetben a tranziens áram maximális értéke jelentősen meghaladhatja az állandósult áram amplitúdóját. ábrából látható. 4, hol

, a maximális áramerősség körülbelül után következik be. A limitben: .

Így lineáris áramkör esetén a tranziens áram maximális értéke nem haladhatja meg a kényszeráram amplitúdójának kétszeresét:.

Hasonlóan a kondenzátoros lineáris áramkörhöz: ha a kapcsolás pillanatában a kényszerfeszültség megegyezik az amplitúdó értékével és az áramkör időállandója elég nagy, akkor kb. a periódus fele után a kondenzátor feszültsége eléri maximális értékét. , amely nem haladhatja meg a kényszerfeszültség amplitúdójának kétszeresét: .

2. Tranziensek, amikor az induktort leválasztják az áramforrásról

ábra szerinti áramkörben a kulcs kinyitásakor. Az 5. ábra az induktoron áthaladó áram kényszerített összetevője.

Karakterisztikus egyenlet

,

ahol és .

Az első kommutációs törvény szerint

.

Így az áram kifejezése tranziens üzemmódban

és az induktor feszültségét

.

(7)

A (7) elemzés azt mutatja, hogy az induktív elemeket tartalmazó áramkörök nyitásakor nagy túlfeszültségek léphetnek fel, amelyek speciális intézkedések nélkül károsíthatják a berendezést. Valóban, at az induktor feszültségmodulja a kapcsoláskor sokszorosa lesz a forrásfeszültségnek: . R kioltóellenállás hiányában a kulcs nyitóérintkezőire a megadott feszültség kerül, aminek következtében közöttük ív keletkezik.

3. Kondenzátor töltés és kisütés

Amikor a kulcsot az 1-es helyzetbe fordítjuk (lásd 6. ábra), megkezdődik a kondenzátor feltöltésének folyamata:

.

A kondenzátoron lévő feszültség kényszerített összetevője.

A karakterisztikus egyenletből

a gyökér meghatározva . Ezért az időállandó.

A karakterisztikus egyenletet kapcsolás után állítjuk össze az áramkörre. A következő módokon szerezhető be:

Közvetlenül egy (1.2) alakú differenciálegyenlet alapján, azaz. az áramkör elektromágneses állapotát a Kirchhoff-törvények alapján leíró egyenletrendszerből kizárva minden ismeretlen mennyiséget, kivéve egyet, amelyre az egyenletet írják;

Az áramkör bemeneti ellenállásának kifejezésével szinuszos áramon;

A főhatározó kifejezése alapján.

Az 1.4.1. pontban szereplő első módszer szerint differenciálegyenletet kaptunk a feszültségre vonatkozóan u C sorozathoz való kondenzátoron r-L-C-láncok (lásd 1.6. ábra):

amely alapján felírjuk a karakterisztikus egyenletet

.

Megjegyzendő, hogy mivel a lineáris áramkört egyetlen tranziens folyamat fedi le, a karakterisztikus egyenlet gyökei közösek az áramköri ágak feszültségeinek és áramainak minden szabad összetevőjére, amelyek paramétereit a karakterisztikus egyenlet tartalmazza. . Ezért a karakterisztikus egyenlet összeállításának első módszere szerint bármely érték választható mennyiségként, amelyre vonatkozóan felírjuk.

A karakterisztikus egyenlet összeállítása a bemeneti ellenállás módszer szerint a következő:

1. Egy kifejezést írunk az áramkör bemeneti ellenállására váltakozó áramú in összetett forma ;

2. Az eredményül kapott kifejezésben jω az üzemeltető helyettesíti R;

3. Az eredményül kapott kifejezést nullára állítjuk.

Az egyenlet egybeesik a jellemzővel.

Hangsúlyozni kell, hogy a bemeneti ellenállás az áramkör bármely ágának töréspontjához viszonyítva írható fel. Ebben az esetben az energiaforrások ki vannak zárva az áramkörből, és belső ellenállásaik a helyükön maradnak.

A karakterisztikus egyenlet összeállításának ez a módszere feltételezi, hogy az elektromos áramkörben nincsenek mágnesesen csatolt ágak. Ha vannak ilyenek, akkor mágneses szétkapcsolást kell végezni.

A vizsgált áramkörhöz (lásd az 1.6. ábrát) a bemeneti ellenállás módszer szerint a következőket kapjuk:

;

;

.

A fődetermináns kifejezése alapján karakterisztikus egyenlet összeállításánál a felírás alapjául szolgáló algebrai egyenletek száma megegyezik az ismeretlen szabadáram-összetevők számával.

Az eredeti, például Kirchhoff-törvények alapján vagy hurokáramok módszerével összeállított integro-differenciálegyenlet-rendszer algebrazását úgy hajtjuk végre, hogy a differenciálási, illetve az integrálási műveleteket szorozzuk és osztjuk operátor R. A karakterisztikus egyenletet úgy kapjuk meg, hogy az írott determinánst nullával egyenlővé tesszük.

Mivel a fődetermináns kifejezése nem függ az inhomogén egyenletrendszer megfelelő részeitől, ezért összeállítható egy összáramokra felírt egyenletrendszer alapján.

A vizsgált sémához (lásd az 1.6. ábrát) a szabad módhoz a következőket találjuk:

.

Az egyenletben a derivált és az integrál lecserélésével, ahogy fentebb említettük, azt kapjuk algebrai egyenlet

vagy .

Hová jutunk

vagy .

) DE = ||aik||n 1 úgy, hogy az átlós elemekből kivonjuk a λ értéket. Ez a determináns egy polinom X-ben – a karakterisztikus polinomban. Nyílt formában X. at. így van írva:

ahol S1 = egy 11 + a 22 +... Ann- ún. nyom mátrix, S2- az összes 2. rendű főkiskorú, azaz az i k) formájú kiskorú stb. összege, és S n- mátrix meghatározó DE. Roots H. u. λ 1 , λ 2 ,..., λ n a mátrix sajátértékeinek nevezzük DE. Valódi szimmetrikus mátrixhoz, valamint hermitikus mátrixhoz mind λ k valódiak, egy valódi ferde-szimmetrikus mátrixban minden λ van k tisztán képzeletbeli számok; valós ortogonális mátrix, valamint unitárius mátrix esetén mind |λ k| = 1.

HU. a matematika, mechanika, fizika, technológia legkülönbözőbb területein megtalálható. A csillagászatban a bolygók világi perturbációinak meghatározásakor X.-hez is eljutnak .-nál; innen ered a H. u. - világi egyenlet.

2) X. y. lineáris differenciálegyenlet -val állandó együtthatók

egy 0λ y (n) + egy 1 év (n-1) +... + a n-1 y" + Bármi = 0

Az az algebrai egyenlet, amely függvényváltás után az adott differenciálegyenletből adódik nál nélés származékai λ megfelelő hatványaival, azaz az egyenlet

egy 0λ n + egy 1λ n-1 + ... + a n-1 y" + Bármi = 0.

Erre az egyenletre akkor jutunk, amikor az alak adott megoldását találjuk nál nél = se λ x adott differenciálegyenlethez. Lineáris differenciálegyenlet-rendszerhez

HU. determináns használatával írva

HU. mátrixok A =

Nagy szovjet enciklopédia. - M.: Szovjet enciklopédia. 1969-1978 .

Nézze meg, mi a "karakterisztikus egyenlet" más szótárakban:

Sok esetben fizikai folyamatok rendszerekben előforduló közönséges lineáris differenciálegyenletek rendszere írja le állandó együtthatókkal, amelyek meglehetősen általános esetben differenciálegyenletre redukálhatók ... Technológia enciklopédiája

A Determináns alakú algebrai egyenlet ebben a képletben a mátrix determinánsából adódik úgy, hogy az átlós elemekből kivonjuk x-et; ez egy polinom x-ben, és karakterisztikus polinomnak nevezzük... Nagy enciklopédikus szótár

karakterisztikus egyenlet- - [V.A. Szemenov. Angol orosz relévédelem szótár] Témák relévédelem EN karakterisztikus egyenlet ... Műszaki fordítói kézikönyv

A forma algebrai egyenlete. Ebben a képletben a determinánst az átlós elemek x mátrixának determinánsából kapjuk; ez egy polinom x-ben, és karakterisztikus polinomnak nevezzük. * * * JELLEMZŐ…… enciklopédikus szótár

karakterisztikus egyenlet- jellemzőoji lygtis statusas T terület automatika atitikmenys: engl. karakterisztikus egyenlet; teljesítményegyenlet vok. characteristische Gleichung, f; Stammgleichung, f rus. karakterisztikus egyenlet, npranc. équation caractéristique, f … Automatikos terminų žodynas

karakterisztikus egyenlet- jellemzőoji lygtis statusas T sritis fizika atitikmenys: engl. karakterisztikus egyenlet; teljesítményegyenlet vok. characteristische Gleichung, f rus. karakterisztikus egyenlet, npranc. équation caractéristique, f … Fizikos terminų žodynas

karakterisztikus egyenlet Enciklopédia "Repülés"

karakterisztikus egyenlet- karakterisztikus egyenlet. A rendszerekben lezajló fizikai folyamatokat sok esetben egy közönséges lineáris differenciálegyenlet-rendszer írja le, állandó együtthatókkal, amelyek meglehetősen általános esetben redukálhatók… Enciklopédia "Repülés"

Az ősrégi egyenlet, lásd az Art. Karakterisztikus polinom … Matematikai Enciklopédia

A karakterisztikus polinom egy olyan polinom, amely egy mátrix sajátértékeit határozza meg. Egy másik jelentés: A lineáris ismétlődés karakterisztikus polinomja egy polinom. Tartalom 1 Definíció ... Wikipédia

Könyvek

• Karakterisztikus hazugsággyűrűk és nemlineáris integrálható egyenletek, Zhiber A.V.