Definiție. ecuație caracteristică operator liniar f este o ecuație de forma , unde λ este oricare numar real, А este matricea operatorului liniar, Е este matricea de identitate de același ordin.
Polinom numit polinom caracteristic matricea A (operatorul liniar f). Sub formă de matrice, ecuația caracteristică are următoarea formă:
 sau
sau
 .
.
Prin urmare, echivalând polinomul caracteristic cu zero, obținem o ecuație de grad n, unde λ acționează ca o necunoscută, obținem valorile rădăcinilor sale - numerele caracteristice ale acestei matrice. Rădăcinile caracteristice joacă un rol important în multe ramuri ale matematicii. Luați în considerare una dintre aplicațiile rădăcinilor caracteristice - un instrument foarte important în studiu spații liniare, precum și în rezolvarea multor probleme aplicate ale algebrei liniare.
Mulțimea tuturor rădăcinilor ecuației caracteristice se numește spectrul operatorului f(fiecare rădăcină este considerată cu multiplicitatea pe care o are în ecuația caracteristică).
Exemplu. Aflați rădăcinile caracteristice ale matricei.
Să facem o matrice

Echivalând polinomul caracteristic cu zero, obținem ecuație pătratică
Atunci rădăcinile ecuației sunt ![]() .
.
Definiție. Fie f un operator spațial liniar și un vector diferit de zero care satisface egalitatea
unde este un număr real. Atunci vectorul se numește vectorul propriu al operatorului și matricea definiției sale, - valoarea proprie sau valoarea proprie a transformării. În acest caz, se spune că vectorul propriu se referă la valoarea proprie.
Vectorii proprii joacă un rol important, atât în matematică în sine, cât și în aplicațiile sale. De exemplu, o rezonanță la care frecvențele naturale ale oscilațiilor sistemului coincid cu frecvența oscilațiilor forțe externe. În matematică, vectorii proprii sunt utili în rezolvarea sistemelor ecuatii diferentiale.
Teorema. Dacă operatorul liniar f în bază (prima bază) are matricea A iar în bază (a doua bază) - matricea B, atunci egalitatea are loc: .
În consecință, la trecerea la o nouă bază, polinomul caracteristic al operatorului liniar nu se modifică.
◌ Dacă T este matricea de tranziție de la prima bază la a doua, atunci . Apoi transformăm partea dreaptă a egalității ●
Teorema. Pentru ca numărul λ 0 din câmpul Р să fie o valoare proprie a vectorului spațiului L n peste Р este necesar și suficient ca numărul λ 0 să fie rădăcina caracteristică a operatorului f.
Doc. eu. Nevoie. Lasa λ 0 operator valoare proprie f, apoi în L n există un vector propriu astfel încât .
Lasa ![]() este șirul său de coordonate într-o anumită bază, atunci
este șirul său de coordonate într-o anumită bază, atunci
Pe de altă parte, din moment ce , unde este matricea operatorului liniar în baza dată, atunci
Echivalând părțile corecte ale (1) și (2) obținem:
 (3)
(3)
Egalitățile (3) înseamnă că vectorul numeric cu coordonate ![]() este o soluție a următorului sistem de ecuații (4).
este o soluție a următorului sistem de ecuații (4).
 (4)
(4)
Vectorul este diferit de zero (pentru că este propriu), deci sistemul (4) are o soluție diferită de zero, deci determinantul său este 0.
 (5)
(5)
și, prin urmare, determinantul transpus este 0.
![]() (6)
(6)
În acest fel, λ 0 este rădăcina ecuației caracteristice.
II. Adecvarea. Lasa λ 0
este rădăcina caracteristică a operatorului în anumite baze ![]() . Să demonstrăm asta λ 0
este o valoare proprie a operatorului A.
. Să demonstrăm asta λ 0
este o valoare proprie a operatorului A.
Într-adevăr, dacă λ 0 este rădăcina caracteristică, atunci egalitatea (6) va fi valabilă și, prin urmare, egalitatea (5), ceea ce va însemna că sistemul (4) are soluții diferite de zero.
Să alegem o soluție diferită de zero a sistemului (4): un vector numeric ![]() . Atunci egalitățile (3) sunt valabile.
. Atunci egalitățile (3) sunt valabile.
Să considerăm un vector , iar egalitatea (2) va fi valabilă pentru el și, în virtutea formulei , egalitatea (1) este adevărată, unde este matricea operatorului în bază ÎN. Aceasta implică egalitatea, ceea ce înseamnă că vectorul este un vector propriu al operatorului, care corespunde valorii proprii. λ 0 . Acesta este ceea ce trebuia dovedit. Teorema a fost demonstrată.
Cometariu. Pentru a găsi valori proprii operator, este necesar să se compună și să se rezolve ecuația (5). Pentru a găsi vectorii proprii ai operatorului, trebuie să compuneți un sistem de ecuații (4) și să găsiți un set fundamental de soluții pentru acest sistem.
Pentru a controla corectitudinea calculului valorilor proprii (pot fi coincidente, complexe), sunt utilizate două fapte:
1)  , unde ultima sumă a urmei matricei este suma elementelor diagonale.
, unde ultima sumă a urmei matricei este suma elementelor diagonale.
2)  .
.
Exemplu. Găsiți valori proprii și vectori proprii  .
.
 Echivalând cu zero obținem . .
Echivalând cu zero obținem . .
3) . , ![]() .
.

Fie o variabilă liberă, apoi obținem un vector  .
.
Exercitiul. Verificați vectorul.
 .
.
Ecuația caracteristică are forma:
Pentru a determina tipul de componentă liberă, este necesar să se compună și să se rezolve ecuația caracteristică: z(p) = 0. Pentru a scrie ecuația caracteristică, este necesar să se deseneze o diagramă în care să fie înlocuite toate sursele de EMF și curent. prin propriul lor intern rezistență, și rezistență inductanța și, respectiv, capacitatea, sunt egale cu Pl și, atunci este necesar să rupeți orice ramură a acestui circuit, să scrieți rezistența sa inițială în raport cu punctele de rupere, să o echivalați cu zero, să rezolvați și să determinați rădăcinile p, dacă rădăcinile s-a dovedit a fi negativ real, apoi componenta liberă a funcției dorite:
 , unde m este numărul de rădăcini ale ecuației;
, unde m este numărul de rădăcini ale ecuației;
Rădăcini; -integrabil constant.
Dacă rădăcinile ecuației caracterului s-au dovedit a fi conjugate complexe, atunci starea liberă va arăta astfel:
 unde este frecventa vibratii libere;
unde este frecventa vibratii libere;
Faza inițială a oscilațiilor libere.
8. Timp tranzitoriu. Definiție practic t pp. Calculul timpului procesului de tranziție.
Timpul procesului de tranziție depinde de coeficientul de atenuare.Reciproca lui , se numește constantă de timp și este timp, în timpul care valoarea componentei libere a tranzitoriului va scădea de e=2,72 ori. Valoarea depinde de circuit și parametri.Deci pentru un circuit cu o conexiune serială r și L = , și cu o conexiune serială
95% sfârşitul tranzitoriului 3 .
Curbele componentelor libere ale procesului tranzitoriu sunt cel mai ușor de construit prin setarea timpului t la valorile 0, ,2 ..... Dacă există mai multe rădăcini reale, atunci curba rezultată se obține prin însumarea ordonatelor a termenilor individuali (Fig. 1.)
Poza 1:

9.10, Proces tranzitoriu în r, C - circuite atunci când este pornit la o sursă de tensiune constantă. Analiza se efectuează prin metoda clasică; dați expresii analitice pentru U C (t); i C (t); grafice. (Metoda clasică).
Ecuația de stare a circuitului rC după comutare este următoarea:
![]() (1) sau rC (2)
(1) sau rC (2)
Solutia lui: ![]()
Capacitatea C după închiderea cheii la t va fi încărcată la o valoare constantă Componentă liberă
Întrucât condițiile inițiale sunt zero, conform legii de comutație ![]() la t=0, sau 0=A, de unde A=-E.
la t=0, sau 0=A, de unde A=-E.
Rezolvarea ecuației (2) va lua forma:
Curentul în circuit i(t)=C
Poza 1.

Figura 2.

Graficele variației tensiunii și curentului i(t) sunt prezentate în figurile 1 și 2. Din figuri se poate observa că tensiunea de pe condensator crește exponențial de la 0 la E, în timp ce puterea curentului în momentul comutării atinge brusc valoarea E/r, apoi scade la zero.
11.12 Proces tranzitoriu în circuitele r, C atunci când sunt conectate la o sursă de tensiune sinusoidală. Analiza se efectuează prin metoda clasică; dați expresii analitice pentru U C (t); i C (t); grafice. (Metoda clasică).

Ecuația de stare pentru un circuit rC în modul tranzitoriu este următoarea
rc ![]() .
.
Rezolvarea acestei ecuații:
![]()
Componentă gratuită
![]() unde =rC
unde =rC
Deoarece circuitul este liniar, atunci cu o acțiune sinusoidală și în stare staționară, tensiunea de pe capacitate se va modifica și ea conform unei legi sinusoidale cu frecvența acțiunii de intrare, Prin urmare, pentru a determina =, vom folosi metoda de amplitudini complexe:
![]() ;
; 
![]()
Având în vedere că j= , obținem:
Constanta de integrare A a componentei libere
Găsiți de la condiții inițialeîn circuit, ținând cont de legea comutației:
![]() .Când t=0, ultima expresie are forma
.Când t=0, ultima expresie are forma
Unde este A=-
Adăugând componentele și , obținem expresia finală pentru tensiunea la nivelul capacității în modul tranzitoriu:
= + = ![]() - (1)
- (1)
Analiza expresiei (1) arată că procesul tranzitoriu în circuitul rC sub acțiune sinusoidală depinde de faza inițială a FEM a sursei în momentul comutării și de constanta de timp a circuitului rC.
Dacă , atunci = 0 și în circuit imediat după comutare, va apărea o stare staționară, adică
Când tensiunea \u003d -, adică. tensiunea capacității imediat după comutare poate atinge aproape dublul valorii semnului pozitiv și apoi se apropie treptat de = .
Diferența de fază va aduce ecuația (1) la forma:
Diferența dintre acest mod și cel anterior este că tensiunea de pe capacitatea imediat după comutare poate atinge aproape dublul semnului negativ.
Pentru circuitul Rc considerat cu o sursă de curent sinusoidală în stare staționară, faza inițială a tensiunii de intrare nu joacă niciun rol, dar influența sa este semnificativă în procesul tranzitoriu.
13. Proces tranzitoriu în r, L, C - circuite atunci când sunt conectate la o sursă de tensiune constantă. proces periodic. Expresii analitice pentru i(t), grafice. (Metoda clasică).
Rădăcinile sunt reale, negative, diferite.
I(t)=I set +A1e p 1 t +A2e p 2 t
proces periodic:
t=0 (i(0)=A1+A2; A1=-A2
{ ![]()
t=0 i l (0)*r+L +Uc(0)=E A1=-A2= ()
i l (t)= ( ![]() )
)
14. Proces tranzitoriu în r, L, C - circuite atunci când sunt conectate la o sursă de tensiune constantă. proces critic. Expresii analitice pentru i(t), grafice. (Metoda clasică).
i l (t)=i set +(B1+B2*t)*
t=0: i l (0)=β1=0
![]()
Dacă rădăcinile s-au dovedit a fi reale, negative, egale, atunci procesul este critic.

15. Proces tranzitoriu în r, L, C - circuite atunci când sunt conectate la o sursă de tensiune constantă. proces oscilator. Expresie analitică pentru i(t), grafică. (Metoda clasică).
P t = -δ±j*ω sv ω sv=
Rădăcinile sunt negative reale, conjugate parțial complexe.
i l (t)=i set A1e - δt *sin(ω st t+ψ)

i l (t)=i set +(M*cos ω St t+N*sin ω St t)*
i l (t) = * ![]() = *
= *

16. Proces tranzitoriu în r, L, C - circuite atunci când este conectat la o sursă de tensiune sinusoidală. proces aperiodic. Expresie analitică pentru i(t), grafică. (Metoda clasică).
R(t)=Emax *sin(ωt+ψ)
2. 
În cazul clasic, numărul de ecuații în acest caz este egal cu numărul de ramuri de circuit
Metoda găsește o soluție sub forma sumei unei soluții generale și a unei soluții particulare. Calculul procesului tranzitoriu este descris printr-un sistem de ecuații diferențiale obișnuite, compilat prin una dintre metodele de calcul pentru valorile instantanee ale funcțiilor de timp. Soluția pentru fiecare variabilă a acestui sistem se găsește ca sumă a soluțiilor generale și particulare. Pentru alcătuirea ecuației se pot folosi: o metodă bazată pe aplicarea legilor lui Kirchhoff, metoda potențialelor nodale, metoda curenților de buclă etc. De exemplu, sistemul de ecuații diferențiale, compilat după comutare conform primei și a doua legi Kirchhoff, are forma:
De exemplu,
Numărul de ecuații în acest caz este egal cu numărul de ramuri de circuit. Să fie necesar să se găsească curentul i k în ramura cu numărul K. Eliminând curenții ramurilor în serie, ca urmare, obținem curentul i k și derivatele lui până la ordinul n:

Ordinea ecuației diferențiale n este determinată de numărul de elemente de circuit reactive independente (m). De obicei n=m, dar în funcție de metoda de conectare, este posibil ca n Elementele capacitive conectate în serie pot fi înlocuite cu un singur element, la fel cum elementele inductive conectate în paralel pot fi înlocuite cu un element echivalent. Figura 9.5 prezintă înlocuirea a 2 rezervoare în serie cu un echivalent. În cazul general, ordinea ecuației diferențiale n este: n=n lc -n ce -n lj , unde n lc este numărul de elemente reactive (L și C) din circuit, n ce este numărul de capacitive circuite, n lj este numărul de noduri sau secțiuni inductive. Capacitiv este înțeles ca un circuit format din elemente capacitive sau elemente capacitive și surse ideale de EMF, Fig. 9.6.a. Inductiv este înțeles ca un nod în care converg ramuri inductive sau ramuri inductive și sursele de curent (Fig. 9.6.b), sau secțiuni care traversează numai ramuri inductive sau ramuri inductive și surse de curent. Rețineți că etapa de compilare a unei ecuații diferențiale nu este obligatorie și curentul sau tensiunea tranzitorie pot fi găsite fără a compila o ecuație. După cum sa indicat, în metoda clasică de calcul al proceselor tranzitorii, rezolvarea ecuațiilor O anumită soluție descrie un mod numit forțat. Rezolvarea unei ecuații omogene (partea dreaptă este egală cu zero) descrie procesul în absența EMF externă și a surselor de curent și se numește liberă. În consecință, se iau în considerare curenții liberi și forțați, tensiunile și sarcinile. Astfel, curentul din ramura cu numărul K este reprezentat ca o sumă. Ecuația caracteristică este compilată pentru circuit după comutare. Poate fi obținut în următoarele moduri: Direct pe baza unei ecuații diferențiale de forma (1.2), i.e. prin excluderea din sistemul de ecuații care descriu starea electromagnetică a circuitului pe baza legilor lui Kirchhoff, a tuturor mărimilor necunoscute, cu excepția uneia, în raport cu care se scrie ecuația; Prin utilizarea expresiei pentru rezistența de intrare a circuitului pe un curent sinusoidal; Pe baza expresiei determinantului principal. Conform primei metode din 1.4.1, a fost obținută o ecuație diferențială în raport cu tensiunea u C pe un condensator pentru serie r-L-C-lanturi (vezi fig. 1.6): pe baza cărora se scrie ecuaţia caracteristică Trebuie remarcat faptul că, deoarece circuitul liniar este acoperit de un singur proces tranzitoriu, rădăcinile ecuației caracteristice sunt comune tuturor componentelor libere ale tensiunilor și curenților ramurilor circuitului, ai căror parametri sunt incluși în ecuația caracteristică. . Prin urmare, conform primei metode de compilare a ecuației caracteristice, orice valoare poate fi aleasă ca mărime în raport cu care este scrisă. Compilarea ecuației caracteristice conform metodei rezistenței de intrare este următoarea: 1. Expresia pentru rezistența de intrare a circuitului pe curent alternativ se scrie sub formă complexă; 2. În expresia rezultată jω este înlocuit de operator R; 3. Expresia rezultată este setată la zero. Ecuația coincide cu cea caracteristică. Trebuie subliniat faptul că rezistența de intrare poate fi scrisă relativ la punctul de rupere a oricărei ramuri a circuitului. În acest caz, sursele de energie sunt excluse din circuit, iar rezistențele lor interne rămân la locul lor. Această metodă de compilare a ecuației caracteristice presupune absența ramurilor cuplate magnetic în circuitul electric. Dacă există, este necesar să se efectueze o decuplare magnetică. Pentru circuitul luat în considerare (vezi Fig. 1.6), conform metodei rezistenței de intrare, avem: La compilarea unei ecuații caracteristice pe baza expresiei determinantului principal, numărul de ecuații algebrice pe baza cărora este scrisă este egal cu numărul de componente de curent liber necunoscute. Algebrizarea sistemului original de ecuații integro-diferențiale, compilat, de exemplu, pe baza legilor lui Kirchhoff sau prin metoda curenților de buclă, se realizează prin înlocuirea operațiilor de diferențiere și, respectiv, de integrare, prin înmulțirea și împărțirea la operator R. Ecuația caracteristică se obține prin echivalarea determinantului scris cu zero. Deoarece expresia pentru determinantul principal nu depinde de părțile corecte ale sistemului de ecuații neomogene, ea poate fi compilată pe baza unui sistem de ecuații scris pentru curenții totali. Pentru schema luată în considerare (vezi Fig. 1.6) pentru modul liber avem: Înlocuind derivata și integrala în ecuație, așa cum am menționat mai sus, obținem ecuația algebrică Unde ajungem Ecuația caracteristică este compilată pentru circuit după comutare. Poate fi obținut în următoarele moduri: Conform primei metode, în prelegerea anterioară, a fost obținută o ecuație diferențială pentru tensiunea pe condensator pentru un circuit serie R-L-C, pe baza căreia este scrisă ecuația caracteristică. Trebuie remarcat faptul că, deoarece circuitul liniar este acoperit de un singur proces tranzitoriu, rădăcinile ecuației caracteristice sunt comune tuturor componentelor libere ale tensiunilor și curenților ramurilor circuitului, ai căror parametri sunt incluși în ecuația caracteristică. . Prin urmare, conform primei metode de compilare a ecuației caracteristice, orice variabilă poate fi aleasă ca variabilă în raport cu care este scrisă. Aplicarea celei de-a doua și a treia metode de compilare a ecuației caracteristice va fi luată în considerare folosind exemplul circuitului din Fig. unu. Compilarea ecuației caracteristice conform metodei rezistenței de intrare este următoarea: se înregistrează impedanța de intrare a circuitului pe curent alternativ; jw este înlocuit cu operatorul p; expresia rezultată este setată la zero. Ecuația se potrivește cu caracteristica. Trebuie subliniat faptul că rezistența de intrare poate fi scrisă relativ la punctul de rupere a oricărei ramuri a circuitului. În acest caz, rețeaua activă cu două terminale este înlocuită cu una pasivă, prin analogie cu metoda generatorului echivalent. Această metodă de compilare a ecuației caracteristice presupune absența ramurilor cuplate magnetic în circuit; dacă există, este necesar să se efectueze dezlegarea lor prealabilă. Pentru circuitul din fig. 1 în ceea ce privește terminalele sursă Înlocuind jw cu p și echivalând expresia rezultată cu zero, scriem La compilarea unei ecuații caracteristice pe baza expresiei determinantului principal, numărul de ecuații algebrice pe baza cărora este scrisă este egal cu numărul de componente de curent liber necunoscute. Algebrizarea sistemului original de ecuații integro-diferențiale, compilat, de exemplu, pe baza legilor lui Kirchhoff sau prin metoda curenților de buclă, se realizează prin înlocuirea simbolurilor de diferențiere și, respectiv, de integrare cu înmulțirea și împărțirea cu operator p. Ecuația caracteristică se obține prin echivalarea determinantului scris cu zero. Deoarece expresia pentru determinantul principal nu depinde de părțile corecte ale sistemului de ecuații neomogene, ea poate fi compilată pe baza unui sistem de ecuații scris pentru curenții totali. Pentru circuitul din fig. 1, sistemul algebrizat de ecuații bazat pe metoda curenților de buclă are forma De aici și expresia pentru principalul determinant al acestui sistem Echivalând D cu zero, obținem un rezultat similar cu (1). Metodologie generală de calcul a tranzitorilor prin metoda clasică În cazul general, metoda de calcul al proceselor tranzitorii prin metoda clasică include următorii pași: Exemple de calcul al proceselor tranzitorii prin metoda clasică 1. Tranzitorii în circuitul R-L atunci când este conectat la o sursă de tensiune Astfel de procese au loc, de exemplu, atunci când electromagneții, transformatoarele, motoarele electrice etc. sunt conectate la o sursă de energie. Luați în considerare două cazuri: Conform metodei considerate pentru curentul din circuit din fig. 2 poate fi scris Ecuație caracteristică de unde şi constantă de timp În acest fel, Înlocuind (4) și (5) în relația (3), scriem În conformitate cu prima lege de comutare. Apoi Astfel, curentul din circuit în procesul tranzitoriu este descris de ecuație iar tensiunea pe inductor - prin expresie Forma calitativă a curbelor și corespunzătoare soluțiilor obținute este prezentată în Fig. 3. Cu al doilea tip de sursă, componenta forțată este calculată folosind metoda simbolică: Expresia pentru componenta liberă nu depinde de tipul sursei de tensiune. Prin urmare, De atunci Astfel, ajungem în sfârșit Analiza expresiei rezultate (6) arată: Dacă este semnificativă ca magnitudine, atunci componenta liberă nu scade semnificativ în jumătate de perioadă. În acest caz, valoarea maximă a curentului tranzitoriu poate depăși semnificativ amplitudinea curentului în stare staționară. După cum se poate observa din fig. 4, unde Astfel, pentru un circuit liniar, valoarea maximă a curentului tranzitoriu nu poate depăși de două ori amplitudinea curentului forțat: . În mod similar pentru un circuit liniar cu un condensator: dacă în momentul comutării tensiunea forțată este egală cu valoarea sa de amplitudine și constanta de timp a circuitului este suficient de mare, atunci după aproximativ jumătate din perioadă tensiunea de pe condensator atinge valoarea maximă. , care nu poate depăși de două ori amplitudinea tensiunii forțate: 2. Tranzitorii atunci când inductorul este deconectat de la sursa de alimentare Când cheia este deschisă în circuitul din fig. 5 este componenta forțată a curentului prin inductor. Ecuație caracteristică Unde Conform primei legi de comutare Astfel, expresia curentului în modul tranzitoriu și tensiunea pe inductor Analiza (7) arată că la deschiderea circuitelor care conțin elemente inductive pot apărea supratensiuni mari care, fără a lua măsuri speciale, pot deteriora echipamentul. Într-adevăr, la 3. Încărcarea și descărcarea condensatorului Când cheia este rotită în poziția 1 (vezi Fig. 6), procesul de încărcare a condensatorului începe: Componenta forțată a tensiunii pe condensator. Din ecuația caracteristică rădăcina este determinată 


 este reprezentată ca suma soluțiilor generale și particulare.
este reprezentată ca suma soluțiilor generale și particulare.![]() .
. ;
; ;
;![]() .
. .
. sau
sau  .
. sau
sau ![]() .
.
 .
.
.
(1)

![]()

![]() .
. .
(5)
 .
.![]() ,
,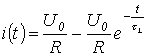 ,
,
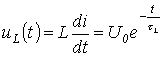 .
. ,
,![]() .
. .
(6)

![]() , curentul maxim apare aproximativ după . În limita la .
, curentul maxim apare aproximativ după . În limita la .![]() .
.
![]() ,
,![]() Și
Și ![]() .
. .
.
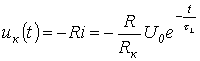 .
.
(7)
![]() modulul de tensiune de pe inductor în momentul comutării va fi de multe ori mai mare decât tensiunea sursei: . În absența unui rezistor de stingere R, tensiunea specificată este aplicată la contactele de deschidere ale cheii, în urma căruia apare un arc între ele.
modulul de tensiune de pe inductor în momentul comutării va fi de multe ori mai mare decât tensiunea sursei: . În absența unui rezistor de stingere R, tensiunea specificată este aplicată la contactele de deschidere ale cheii, în urma căruia apare un arc între ele.
![]() .
.![]() . De aici constanta de timp.
. De aici constanta de timp.