Karakteristična jednadžba se sastavlja za kolo nakon prebacivanja. Može se dobiti na sljedeće načine:

• direktno na osnovu diferencijalne jednadžbe oblika (2) (vidjeti predavanje br. 24), tj. isključivanjem iz sistema jednačina koje opisuju elektromagnetno stanje kola na osnovu prvog i drugog Kirchhoffovog zakona, svih nepoznatih veličina, osim jedne, za koju je napisana jednačina (2);
• korištenjem izraza za ulazni otpor kola na sinusnoj struji;
• na osnovu izraza glavne determinante.

Prema prvoj metodi, u prethodnom predavanju je dobijena diferencijalna jednačina za napon na kondenzatoru za serijski R-L-C kolo, na osnovu koje je napisana karakteristična jednačina.

Treba napomenuti da, budući da je linearni krug pokriven jednim prolaznim procesom, korijenima karakteristična jednačina zajednički su za sve slobodne komponente napona i struja grana kola, čiji su parametri uključeni u karakterističnu jednačinu. Dakle, prema prvoj metodi sastavljanja karakteristične jednadžbe, bilo koja varijabla se može odabrati kao varijabla u odnosu na koju je zapisana.

Primjena druge i treće metode za sastavljanje karakteristične jednadžbe će se razmotriti na primjeru kola na sl. jedan.

Sastavljanje karakteristične jednačine metodom ulaznog otpora je kako slijedi:

snima se ulazna impedancija kola na naizmjeničnu struju;

jw je zamijenjen operatorom p;

rezultirajući izraz je postavljen na nulu.

Jednačina

odgovara karakteristici.

Treba naglasiti da se ulazni otpor može zapisati u odnosu na tačku prekida bilo koje grane kola. U ovom slučaju, aktivna mreža s dva terminala zamjenjuje se pasivnom, po analogiji s metodom ekvivalentnog generatora. Ova metoda sastavljanje karakteristične jednadžbe podrazumijeva odsustvo magnetno spregnutih grana u kolu; ako ih ima potrebno je izvršiti njihovo prethodno odvezivanje.

Za kolo na sl. 1 u odnosu na izvorne terminale

.

Zamijenimo jw sa p i izjednačimo rezultirajući izraz sa nulom, pišemo

.

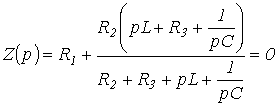
(1)

Prilikom sastavljanja karakteristične jednačine na osnovu izraza glavne determinante, broj algebarskih jednačina na osnovu kojih je napisana jednak je broju nepoznatih komponenti slobodne struje. Algebraizacija originalnog sistema integro- diferencijalne jednadžbe, sastavljen, na primjer, na osnovu Kirchhoffovih zakona ili metodom struja petlje, izvodi se zamjenom simbola diferencijacije i integracije, odnosno množenjem i dijeljenjem operatorom p. Karakteristična jednačina se dobija izjednačavanjem zapisane determinante sa nulom. Pošto izraz za glavnu determinantu ne zavisi od pravih delova sistema nehomogenih jednačina, može se sastaviti na osnovu sistema jednačina napisanih za ukupne struje.

Za kolo na sl. 1, algebraizovani sistem jednačina zasnovan na metodi struja petlje ima oblik

Otuda i izraz za glavnu determinantu ovog sistema

Izjednačavajući D sa nulom, dobijamo rezultat sličan (1).

Opća metodologija za proračun prijelaznih pojava klasičnom metodom

U opštem slučaju, metoda za proračun prolaznih procesa klasičnom metodom uključuje sljedeće korake:

Primjeri proračuna prelaznih procesa klasičnom metodom

1. Procesi tranzicije u R-L lanci kada je priključen na izvor napona

Takvi se procesi odvijaju, na primjer, kada su elektromagneti, transformatori, elektromotori itd. povezani na izvor napajanja.

Razmotrite dva slučaja:

Prema razmatranoj metodi za struju u kolu na sl. 2 se može napisati

Karakteristična jednačina

odakle i vremenska konstanta .

Na ovaj način,

.

(5)

Zamjenom (4) i (5) u relaciju (3) pišemo

.

U skladu sa prvim komutacijskim zakonom. Onda

,

Dakle, struja u kolu u prolaznom procesu je opisana jednadžbom

,

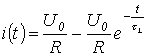a napon na induktoru - po izrazu

.

Kvalitativni oblik krivulja i odgovarajući dobijenim rješenjima prikazan je na Sl. 3.

Kod drugog tipa izvora, prisilna komponenta se izračunava pomoću simboličke metode:

,

Izraz za slobodnu komponentu ne zavisi od vrste izvora napona. shodno tome,

.

Od tada

Dakle, konačno dobijamo

.

(6)

Analiza rezultirajućeg izraza (6) pokazuje:

Ako je značajna po veličini, onda se slobodna komponenta ne smanjuje značajno tokom pola perioda. U ovom slučaju, maksimalna vrijednost prelazne struje može značajno premašiti amplitudu struje stacionarnog stanja. Kao što se može vidjeti sa sl. 4, gdje

, maksimalna struja se javlja otprilike nakon . U limitu na .

Dakle, za linearni krug, maksimalna vrijednost prolazne struje ne može premašiti dvostruku amplitudu prisilne struje: .

Slično za linearni krug s kondenzatorom: ako je u trenutku uključivanja prisilni napon jednak vrijednosti njegove amplitude i vremenska konstanta kola dovoljno velika, tada nakon otprilike polovine perioda napon na kondenzatoru dostiže svoju maksimalnu vrijednost , koji ne može premašiti dvostruku amplitudu prinudnog napona: .

2. Tranzijenti kada je induktor isključen iz izvora napajanja

Kada je ključ otvoren u kolu na sl. 5 je prisilna komponenta struje kroz induktor.

Karakteristična jednačina

,

gdje I .

Prema prvom zakonu o zamjenama

.

Dakle, izraz za struju u prolaznom modu

i napon na induktoru

.

(7)

Analiza (7) pokazuje da pri otvaranju kola koja sadrže induktivne elemente može doći do velikih prenapona koji, bez poduzimanja posebnih mjera, mogu oštetiti opremu. Zaista, kod naponski modul na induktoru u trenutku prebacivanja bit će višestruko veći od napona izvora: . U nedostatku otpornika za gašenje R, navedeni napon se primjenjuje na otvorne kontakte ključa, zbog čega između njih nastaje luk.

3. Punjenje i pražnjenje kondenzatora

Kada se ključ okrene u položaj 1 (vidi sliku 6), počinje proces punjenja kondenzatora:

.

Prisilna komponenta napona na kondenzatoru.

Iz karakteristične jednačine

korijen je određen . Otuda i vremenska konstanta.

Karakteristična jednadžba se sastavlja za kolo nakon prebacivanja. Može se dobiti na sljedeće načine:

Neposredno na osnovu diferencijalne jednadžbe oblika (1.2), tj. isključivanjem iz sistema jednačina koje opisuju elektromagnetno stanje kola na osnovu Kirchhoffovih zakona, svih nepoznatih veličina, osim jedne, u odnosu na koju je jednačina napisana;

Koristeći izraz za ulazni otpor kola na sinusnoj struji;

Na osnovu izraza glavne determinante.

Prema prvoj metodi u 1.4.1, dobijena je diferencijalna jednačina u odnosu na napon u C na kondenzatoru za seriju r-L-C-lanci (vidi sliku 1.6):

na osnovu koje je napisana karakteristična jednačina

.

Treba napomenuti da, budući da je linearni krug pokriven jednim prolaznim procesom, korijeni karakteristične jednadžbe su zajednički za sve slobodne komponente napona i struja grana kola, čiji su parametri uključeni u karakterističnu jednadžbu. . Dakle, prema prvoj metodi sastavljanja karakteristične jednadžbe, bilo koja vrijednost se može odabrati kao veličina u odnosu na koju je zapisana.

Sastavljanje karakteristične jednadžbe prema metodi ulaznog otpora je kako slijedi:

1. Napisan je izraz za ulazni otpor kola na naizmjeničnu struju u složen oblik ;

2. U rezultirajućem izrazu jω zamjenjuje operater R;

3. Rezultirajući izraz je postavljen na nulu.

Jednačina se poklapa sa karakterističnom.

Treba naglasiti da se ulazni otpor može zapisati u odnosu na tačku prekida bilo koje grane kola. U ovom slučaju, izvori energije su isključeni iz kola, a njihovi unutrašnji otpori ostaju na svom mjestu.

Ova metoda sastavljanja karakteristične jednačine pretpostavlja odsustvo magnetno spregnutih grana u električnom kolu. Ako ih ima, potrebno je izvršiti magnetno razdvajanje.

Za kolo koje se razmatra (vidi sliku 1.6), prema metodi ulaznog otpora, imamo:

;

;

.

Prilikom sastavljanja karakteristične jednačine na osnovu izraza glavne determinante, broj algebarskih jednačina na osnovu kojih je napisana jednak je broju nepoznatih komponenti slobodne struje.

Algebraizacija originalnog sistema integro-diferencijalnih jednačina, sastavljenih, na primjer, na osnovu Kirchhoffovih zakona ili metodom struja petlje, izvodi se zamjenom operacija diferencijacije, odnosno integracije, množenjem i dijeljenjem sa operater R. Karakteristična jednačina se dobija izjednačavanjem zapisane determinante sa nulom.

Pošto izraz za glavnu determinantu ne zavisi od pravih delova sistema nehomogenih jednačina, može se sastaviti na osnovu sistema jednačina napisanih za ukupne struje.

Za šemu koja se razmatra (vidi sliku 1.6) za slobodni način rada imamo:

.

Zamjenom izvoda i integrala u jednačini, kao što je gore navedeno, dobijamo algebarska jednačina

ili .

Gde da stignemo

ili .

) ALI = ||aik||n 1 oduzimanjem vrijednosti λ od dijagonalnih elemenata. Ova determinanta je polinom u X - karakteristični polinom. U otvorenom obliku X. at. je napisano ovako:

gdje S1 = a 11 + a 22 +... ann- takozvani. Trace Matrix, S2- zbir svih glavnih minora 2. reda, tj. minora oblika i k), itd., i S n- matrična determinanta ALI. Roots H. u. λ 1 , λ 2 ,..., λ n nazivaju se svojstvene vrijednosti matrice ALI. Za realnu simetričnu matricu, kao i za hermitsku matricu, svi λ k su realne, realna koso-simetrična matrica ima sve λ kčisto imaginarni brojevi; u slučaju realne ortogonalne matrice, kao i unitarne matrice, sve |λ k| = 1.

H. u. nalazi se u raznim oblastima matematike, mehanike, fizike, tehnologije. U astronomiji, kada se određuju sekularne perturbacije planeta, oni takođe dolaze do X. na .; otuda i drugi naziv za H. u. - sekularna jednadžba.

2) X. y. linearna diferencijalna jednadžba sa konstantni koeficijenti

a 0λ y (n) + a 1 g (n-1) +... + a n-1 y" + a n y = 0

Algebarska jednadžba koja proizlazi iz date diferencijalne jednadžbe nakon promjene funkcije at i njegove derivacije po odgovarajućim potencijama λ, tj. jednačina

a 0λ n + a 1λ n-1 + ... + a n-1 y" + a n y = 0.

Do ove jednačine se dolazi prilikom pronalaženja određenog rješenja oblika at = se λ X za datu diferencijalnu jednačinu. Za sistem linearnih diferencijalnih jednadžbi

H. u. napisano pomoću determinante

H. u. matrice A =

Veliki sovjetska enciklopedija. - M.: Sovjetska enciklopedija. 1969-1978 .

Pogledajte šta je "Karakteristična jednačina" u drugim rječnicima:

U mnogim slučajevima fizički procesi, koji se javljaju u sistemima, opisani su sistemom običnih linearnih diferencijalnih jednadžbi sa konstantnim koeficijentima, koji se u prilično opštem slučaju mogu svesti na diferencijalnu jednačinu... Enciklopedija tehnologije

Algebarska jednadžba oblika Determinanta u ovoj formuli se dobija iz determinante matrice oduzimanjem x od dijagonalnih elemenata; to je polinom po x i naziva se karakteristični polinom... Veliki enciklopedijski rječnik

karakteristična jednačina- - [V.A. Semenov. Engleski ruski rječnik relejne zaštite] Teme relejne zaštite EN karakteristična jednačina ... Priručnik tehničkog prevodioca

Algebarska jednadžba oblika. Determinanta u ovoj formuli se dobija iz determinante matrice x dijagonalnih elemenata; to je polinom po x i naziva se karakteristični polinom. * * * KARAKTERISTIKE… … enciklopedijski rječnik

karakteristična jednačina- būdingoji lygtis statusas T sritis automatika atitikmenys: engl. karakteristična jednačina; jednačina performansi vok. characteristische Gleichung, f; Stammgleichung, f rus. karakteristična jednačina, npr. équation caractéristique, f … Automatikos terminų žodynas

karakteristična jednačina- būdingoji lygtis statusas T sritis fizika atitikmenys: engl. karakteristična jednačina; jednačina performansi vok. characteristische Gleichung, f rus. karakteristična jednačina, npr. équation caractéristique, f … Fizikos terminų žodynas

karakteristična jednačina Enciklopedija "Vazduhoplovstvo"

karakteristična jednačina- karakteristična jednačina. U mnogim slučajevima, fizički procesi koji se dešavaju u sistemima opisuju se sistemom običnih linearnih diferencijalnih jednačina sa konstantnim koeficijentima, koji se u prilično opštem slučaju mogu svesti na... Enciklopedija "Vazduhoplovstvo"

Prastara jednačina, vidi čl. Karakteristični polinom … Mathematical Encyclopedia

Karakteristični polinom je polinom koji definira svojstvene vrijednosti matrice. Drugo značenje: Karakteristični polinom linearnog ponavljanja je polinom. Sadržaj 1 Definicija ... Wikipedia

Knjige

• Karakteristični Lie prstenovi i nelinearne integrabilne jednačine, Zhiber A.V.