INFINITE PICCOLE FUNZIONI E LORO PROPRIETÀ FONDAMENTALI

Funzione y=f(x) chiamato infinitesimale A x→a o quando X→∞, se o , cioè una funzione infinitesima è una funzione il cui limite in un dato punto è zero.

Esempi.

Stabiliamo la seguente importante relazione:

Teorema. Se la funzione y=f(x) rappresentabile con x→a come somma di un numero costante B e grandezza infinitesimale α(x): f(x)=b+ α(x) Quello .

Viceversa, se , allora f(x)=b+α(x), Dove ascia)– infinitesimo a x→a.

Prova.

Consideriamo le proprietà di base delle funzioni infinitesime.

Teorema 1. La somma algebrica di due, tre e in generale di qualsiasi numero finito di infinitesimi è una funzione infinitesima.

Prova. Diamo una dimostrazione per due termini. Permettere f(x)=α(x)+β(x), dove e . Dobbiamo dimostrarlo per ogni piccolo ε arbitrario > 0 trovato δ> 0, tale che per X, soddisfacendo la disuguaglianza |x – a|<δ , eseguita |f(x)|< ε.

Quindi, sistemiamo numero arbitrario ε > 0. Poiché secondo le condizioni del teorema α(x)è una funzione infinitesima, allora esiste tale δ 1 > 0, ovvero |x – a|< δ 1 abbiamo |α(x)|< ε / 2. Allo stesso modo, da allora β(x)è infinitesimo, allora esiste tale δ 2 > 0, ovvero |x – a|< δ 2 abbiamo | β(x)|< ε / 2.

Prendiamo δ=min(δ1 , δ2 } .Quindi in prossimità del punto UN raggio δ ciascuna delle disuguaglianze sarà soddisfatta |α(x)|< ε / 2 e | β(x)|< ε / 2. Pertanto, in questo quartiere ci sarà

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,

quelli. |f(x)|< ε, che è ciò che doveva essere dimostrato.

Teorema 2. Il prodotto è infinito piccola funzione ascia) per una funzione limitata f(x) A x→a(o quando x→∞) è una funzione infinitesima.

Prova. Poiché la funzione f(x)è limitato, quindi c'è un numero M tale che per tutti i valori X da qualche intorno di un punto a|f(x)|≤M. Inoltre, da allora ascia)è una funzione infinitesima a x→a, quindi per un ε arbitrario > 0 c'è un intorno del punto UN, in cui vale la disuguaglianza |α(x)|< ε /M. Poi nel più piccolo di questi quartieri abbiamo | αf|< ε /M= ε. E questo significa questo af– infinitesimo. Per l'occasione x→∞ la dimostrazione si svolge in modo simile.

Dal teorema dimostrato segue:

Corollario 1. Se e, allora.

Corollario 2. Se c= const, quindi .

Teorema 3. Rapporto di una funzione infinitesima α(x) per funzione f(x), il cui limite è diverso da zero, è una funzione infinitesima.

Prova. Permettere . Quindi 1 /f(x) c'è una funzione limitata. Quindi la frazione è il prodotto di una funzione infinitesima e di una funzione limitata, cioè la funzione è infinitesima.

RAPPORTO TRA FUNZIONI INFINITAMENTE PICCOLE E INFINITAMENTE GRANDI

Teorema 1. Se la funzione f(x)è infinitamente grande a x→a, quindi funzione 1 /f(x)è infinitesimale a x→a.

Prova. Prendiamo un numero arbitrario ε >0 e dimostrarlo per alcuni δ>0 (a seconda di ε) per tutti X, per cui |x – a|<δ , la disuguaglianza è soddisfatta, e questo significherà questo 1/f(x)è una funzione infinitesima. Infatti, da allora f(x)è una funzione infinitamente grande in x→a, allora ci sarà δ>0 tale che non appena |x – a|<δ , quindi | f(x)|> 1/ ε. Ma poi per lo stesso X.

Esempi.

Si può dimostrare anche il teorema inverso.

Teorema 2. Se la funzione f(x)- infinitesimo a x→a(O x→∞) e non svanisce, quindi y= 1/f(x)è una funzione infinitamente grande.

Esegui tu stesso la dimostrazione del teorema.

Esempi.

Pertanto, le proprietà più semplici delle funzioni infinitesime e infinitamente grandi possono essere scritte utilizzando le seguenti relazioni condizionali: UN≠ 0

TEOREMI LIMITE

Teorema 1. Il limite della somma algebrica di due, tre e generalmente un certo numero di funzioni è uguale alla somma algebrica dei limiti di queste funzioni, cioè

Prova. Effettuiamo la dimostrazione per due termini, poiché si può fare allo stesso modo per qualsiasi numero di termini. Permettere .Poi f(x)=b+α(x) E g(x)=c+β(x), Dove α E β – funzioni infinitesime. Quindi,

f(x) + g(x)=(b + c) + (α(x) + β(x)).

Perché b+cè una costante, e α(x) + β(x)è una funzione infinitesima, quindi

Esempio. .

Teorema 2. Il limite del prodotto di due, tre e generalmente un numero finito di funzioni è uguale al prodotto dei limiti di queste funzioni:

Prova. Permettere . Quindi, f(x)=b+α(x) E g(x)=c+β(x) E

fg = (b + α)(c + β) = bc + (bβ + cα + αβ).

Lavoro avanti Cristo c'è un valore costante. Funzione bβ + cα + αβ in base alle proprietà delle funzioni infinitesime, esiste una quantità infinitesima. Ecco perché .

Corollario 1. Il fattore costante può essere portato oltre il segno limite:

.

Corollario 2. Il grado limite è uguale al grado limite:

.

Esempio..

Teorema 3. Il limite del quoziente di due funzioni è uguale al quoziente dei limiti di queste funzioni se il limite del denominatore è diverso da zero, cioè

.

Prova. Permettere . Quindi, f(x)=b+α(x) E g(x)=c+β(x), Dove α, β – infinitesimo. Consideriamo il quoziente

Una frazione è una funzione infinitesima perché il numeratore è una funzione infinitesima e il denominatore ha un limite c2≠0.

Esempi.

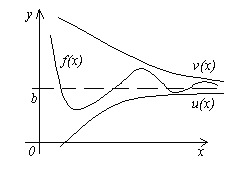
Teorema 4. Siano date tre funzioni f(x), u(x) E v(x), soddisfacendo le disuguaglianze u (x)≤f(x)≤ v(x). Se le funzioni u(x) E v(x) hanno lo stesso limite a x→a(O x→∞), quindi la funzione f(x) tende allo stesso limite, cioè Se

, Quello .

Il significato di questo teorema è chiaro dalla figura.

La dimostrazione del Teorema 4 si trova, ad esempio, nel libro di testo: Piskunov N. S. Differential and integral calculus, vol. 1 - M.: Nauka, 1985.

Teorema 5. Se a x→a(O x→∞) funzione y=f(x) accetta valori non negativi y≥0 e allo stesso tempo tende al limite B, allora questo limite non può essere negativo: b≥0.

Prova. Effettueremo la dimostrazione per assurdo. Facciamo finta che B<0 , Poi |y – b|≥|b| e, quindi, il modulo differenziale non tende a zero quando x→a. Ma allora sì non raggiunge il limite B A x→a, il che contraddice le condizioni del teorema.

Teorema 6. Se due funzioni f(x) E g(x) per tutti i valori dell'argomento X soddisfare la disuguaglianza f(x)≥ g(x) e hanno dei limiti, allora vale la disuguaglianza b≥c.

Prova. Secondo le condizioni del teorema f(x)-g(x) ≥0, quindi, dal Teorema 5 , O .

LIMITI UNILATERALI

Finora abbiamo considerato la determinazione del limite di una funzione quando x→a in modo arbitrario, cioè il limite della funzione non dipendeva da come era posizionata X in direzione UN, a sinistra o a destra di UN. Tuttavia, è abbastanza comune trovare funzioni che non hanno limiti in questa condizione, ma hanno un limite se x→a, rimanendo su un lato di UN, sinistra o destra (vedi figura). Pertanto, vengono introdotti i concetti di limiti unilaterali.

Se f(x) tende al limite B A X tendente ad un certo numero UN COSÌ X accetta solo valori inferiori a UN, poi scrivono e chiamano blimite della funzione f(x) nel punto a a sinistra.

Funzione y=f(x) chiamato infinitesimale A x→a o quando X→∞, se o , cioè una funzione infinitesima è una funzione il cui limite in un dato punto è zero.

Esempi.

1. Funzione f(x)=(X-1) 2 è infinitesimale a X→1, poiché (vedi figura).

2. Funzione f(x)= tg X– infinitesimo a X→0.

3. f(x)= logaritmo(1+ X) – infinitesimo a X→0.

4. f(x) = 1/X– infinitesimo a X→∞.

Stabiliamo la seguente importante relazione:

Teorema. Se la funzione y=f(x) rappresentabile con x→a come somma di un numero costante B e grandezza infinitesimale α(x): f(x)=b+ α(x) Quello .

Viceversa, se , allora f(x)=b+α(x), Dove ascia)– infinitesimo a x→a.

Prova.

1. Dimostriamo la prima parte dell'affermazione. Dall'uguaglianza f(x)=b+α(x) Dovrebbe |f(x) – b|=| α|. Ma da allora ascia)è infinitesimale, allora per ε arbitrario esiste δ – un intorno del punto UN, davanti a tutti X da cui, valori ascia) soddisfare la relazione |α(x)|< ε. Poi |f(x) – b|< ε. E questo significa che.

2. Se , allora per qualsiasi ε >0 per tutti X da qualche δ – intorno di un punto UN Volere |f(x) – b|< ε. Ma se denotiamo f(x) – b=α, Quello |α(x)|< ε, il che significa questo UN– infinitesimo.

Consideriamo le proprietà di base delle funzioni infinitesime.

Teorema 1. La somma algebrica di due, tre e in generale di qualsiasi numero finito di infinitesimi è una funzione infinitesima.

Prova. Diamo una dimostrazione per due termini. Permettere f(x)=α(x)+β(x), dove e . Dobbiamo dimostrarlo per ogni piccolo ε arbitrario > 0 trovato δ> 0, tale che per X, soddisfacendo la disuguaglianza |x – a|<δ , eseguita |f(x)|< ε.

Quindi, fissiamo un numero arbitrario ε > 0. Poiché secondo le condizioni del teorema α(x)è una funzione infinitesima, allora esiste tale δ 1 > 0, ovvero |x – a|< δ 1 abbiamo |α(x)|< ε / 2. Allo stesso modo, da allora β(x)è infinitesimo, allora esiste tale δ 2 > 0, ovvero |x – a|< δ 2 abbiamo | β(x)|< ε / 2.

Prendiamo δ=min(δ1 , δ2 } .Quindi in prossimità del punto UN raggio δ ciascuna delle disuguaglianze sarà soddisfatta |α(x)|< ε / 2 e | β(x)|< ε / 2. Pertanto, in questo quartiere ci sarà

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,

quelli. |f(x)|< ε, che è ciò che doveva essere dimostrato.

Teorema 2. Prodotto di una funzione infinitesima ascia) per una funzione limitata f(x) A x→a(o quando x→∞) è una funzione infinitesima.

Prova. Poiché la funzione f(x)è limitato, quindi c'è un numero M tale che per tutti i valori X da qualche intorno di un punto a|f(x)|≤M. Inoltre, da allora ascia)è una funzione infinitesima a x→a, quindi per un ε arbitrario > 0 c'è un intorno del punto UN, in cui vale la disuguaglianza |α(x)|< ε /M. Poi nel più piccolo di questi quartieri abbiamo | αf|< ε /M= ε. E questo significa questo af– infinitesimo. Per l'occasione x→∞ la dimostrazione si svolge in modo simile.

Dal teorema dimostrato segue:

Corollario 1. Se e, allora.

Corollario 2. Se c= const, quindi .

Teorema 3. Rapporto di una funzione infinitesima α(x) per funzione f(x), il cui limite è diverso da zero, è una funzione infinitesima.

Prova. Permettere . Quindi 1 /f(x) c'è una funzione limitata. Pertanto, una frazione è il prodotto di una funzione infinitesima e di una funzione limitata, cioè la funzione è infinitesima.

Definizione funzione numerica. Metodi per specificare le funzioni.

Sia D un insieme sulla retta R. Se a ogni x appartenente a D è associato un singolo numero y=f(x), allora diciamo che è data una funzione f.

Metodi per specificare le funzioni:

1) tabulare – per funzioni definite su un insieme finito.

2) analitico

3) grafico

2 e 3 – per funzioni definite su un insieme infinito.

Il concetto di funzione inversa.

Se la funzione y=f(x) è tale che corrispondono diversi valori dell'argomento x significati diversi y, allora la variabile x può essere espressa come funzione della variabile y: x=g(y). La funzione g è detta inversa di f ed è denotata con f^(-1).

Il concetto di funzione complessa.

Complesso funzione-funzione, il cui argomento è qualsiasi altra funzione.

Siano date le funzioni f(x) e g(x). Facciamo due funzioni complesse da loro. Considerando la funzione f esterna (principale) e la funzione g interna, otteniamo funzione complessa u(x)=f(g(x)).

Determinazione del limite della sequenza.

Un numero a è detto limite di una successione (xn) se per ogni positivo esiste un numero n0, a partire dal quale tutti i termini della successione differiscono da a in modulo per meno di ε (cioè rientrano nell'intorno ε del punto a):

Regole per il calcolo dei limiti di successioni convergenti.

1. Ogni successione convergente ha un solo limite. 2. Se tutti gli elementi della sequenza (x n) sono uguali a C (costante), anche il limite della sequenza (x n) è uguale a C. 3. ; 4. ; 5. .

Definizione di sequenza limitata.

La successione (x n) si dice limitata se l'insieme dei numeri X=(x n) è limitato: .

Definizione di successione infinitesima.

La successione (x n) si dice infinitesima se per ogni (non importa quanto piccolo) >0 esiste un numero n 0 tale che per ogni n>n 0 la disuguaglianza |x n |< .

Definizione di successione infinitamente grande.

Una successione si dice infinitamente grande se per ogni numero A>0 (non importa quanto grande) esiste un numero n 0 tale che per ogni numero n>n 0 vale la disuguaglianza |x n |>A.

Definizione di successioni monotone.

Sequenze monotone: 1) crescente sex n x n +1 per tutti gli n, 4) non crescente se x n x n +1 per tutti gli n.

Determinazione del limite di una funzione in un punto.

Il limite della funzione y=f(x) nel punto x 0 (o in x x 0) è il numero a se per qualsiasi sequenza (x n) valori dell'argomento converge a x 0 (tutti x n x 0), Il sequenza di (f(x n)) valori della funzione converge al limite a.

Definizione di funzione infinitesima.

Coraggio f(x) si dice infinitesimo come x→A se .

La definizione è infinita grandi funzioni.

Coraggio f(x) si dice infinitamente grande per x→A se .

Def: La funzione viene chiamata infinitesimale a , se .

Nella notazione “ ” lo assumeremo x0 può assumere come valore finale: x0= Сonst e infinito: x0= ∞.

Proprietà delle funzioni infinitesime:

1) La somma algebrica di un numero finito di funzioni infinitesime è una somma infinitesima di funzioni.

2) Il prodotto di un numero finito di funzioni infinitesime è una funzione infinitesima.

3) Lavoro funzione limitata a una funzione infinitesima è una funzione infinitesima.

4) Il quoziente di divisione di una funzione infinitesima per una funzione il cui limite è diverso da zero è una funzione infinitesima.

Esempio: Funzione sì = 2 + Xè infinitesimo in , perché .

Def: La funzione viene chiamata infinitamente grande a , se .

Proprietà delle funzioni infinitamente grandi:

1) La somma di funzioni infinitamente grandi è una funzione infinitamente grande.

2) Il prodotto di una funzione infinitamente grande e di una funzione il cui limite è diverso da zero è una funzione infinitamente grande.

3) La somma di una funzione infinitamente grande e di una funzione limitata è una funzione infinitamente grande.

4) Il quoziente di divisione di una funzione infinitamente grande per una funzione che ha un limite finito è una funzione infinitamente grande.

Esempio: Funzione sì= è infinitamente grande in , perché .

Teorema.Relazione tra quantità infinitamente piccole e infinitamente grandi. Se una funzione è infinitesima in , allora la funzione è infinitamente grande in . E viceversa, se una funzione è infinitamente grande in , allora la funzione è infinitesimale in .

Il rapporto tra due infinitesimi è solitamente indicato con il simbolo e il rapporto tra due infinitesimi con il simbolo. Entrambe le relazioni sono indefinite nel senso che il loro limite può esistere o meno, essere uguale a un certo numero o essere infinito, a seconda del tipo di funzioni specifiche incluse nelle espressioni indefinite.

Oltre alle incertezze di tipo e alle incertezze, le seguenti espressioni sono:

Differenza di infinitamente grandi dello stesso segno;

Il prodotto di un infinitesimo per un infinitamente grande;

Una funzione esponenziale la cui base tende a 1 e l'esponente tende a ;

Una funzione esponenziale la cui base è infinitesima e il cui esponente è infinitamente grande;

Una funzione esponenziale la cui base ed esponente sono infinitesimali;

Una funzione esponenziale la cui base è infinitamente grande e il cui esponente è infinitesimo.

Si dice che vi sia un'incertezza del tipo corrispondente. In questi casi viene chiamato il calcolo del limite rivelando incertezza. Per rivelare l'incertezza, l'espressione sotto il segno limite viene convertita in una forma che non contiene incertezza.

Quando si calcolano i limiti, vengono utilizzate le proprietà dei limiti, nonché le proprietà delle funzioni infinitesimali e infinitamente grandi.

Diamo un'occhiata ad esempi di calcoli di vari limiti.

1) . 2) .

4) , Perché prodotto di una funzione infinitesima e di una funzione limitata è infinitesimale.

5) . 6) .

7) = =

. In questo caso si è verificata un'incertezza di tipo, che è stata risolta fattorizzando i polinomi e riducendoli ad un fattore comune.

= .

In questo caso si trattava di un'incertezza di tipo , che è stata risolta moltiplicando numeratore e denominatore per l'espressione, utilizzando la formula, e quindi riducendo la frazione per (+1).

9)
. In questo esempio, l'incertezza del tipo è stata rivelata dividendo il numeratore e il denominatore della frazione per la potenza iniziale.

Limiti meravigliosi

Il primo meraviglioso limite : .

Prova. Consideriamo la circonferenza unitaria (Fig. 3).

Fig.3. Cerchio unitario

Permettere X– misura in radianti dell'angolo al centro MOA(), Poi OA = R= 1, MK= peccato X, A= tg X. Confronto tra le aree dei triangoli OMA, OTA e settori OMA, noi abbiamo:

,

.

Dividere l'ultima disuguaglianza per il peccato X, noi abbiamo:

.

Poiché a , allora per la proprietà 5) limiti

Da qui deriva il valore inverso, che è quello che doveva essere dimostrato.

Commento: Se la funzione è infinitesima in , cioè , allora il primo limite notevole ha la forma:

.

Diamo un'occhiata ad esempi di calcoli dei limiti utilizzando il primo limite notevole.

Nel calcolare questo limite abbiamo utilizzato formula trigonometrica: .

.

Diamo un'occhiata ad esempi di calcoli dei limiti utilizzando il secondo limite notevole.

2) .

3) . C'è incertezza sul tipo. Facciamo una sostituzione, allora; A .

Calcolo degli infinitesimi e dei grandi

Calcolo infinitesimale- calcoli eseguiti con quantità infinitesime, in cui il risultato derivato è considerato come una somma infinita di infinitesimi. Il calcolo infinitesimale lo è concetto generale per il calcolo differenziale e integrale, che costituiscono la base della moderna matematica superiore. Il concetto di quantità infinitesima è strettamente correlato al concetto di limite.

Infinitesimale

Sotto sequenza UN N chiamato infinitesimale, Se . Ad esempio, una sequenza di numeri è infinitesima.

La funzione viene chiamata infinitesimale in prossimità di un punto X 0 se .

La funzione viene chiamata infinitesimo all'infinito, Se O .

Anche infinitesimale è una funzione che è la differenza tra una funzione e il suo limite, cioè se , Quello F(X) − UN = α( X) , .

Quantità infinitamente grande

In tutte le formule seguenti, è implicito che l'infinito a destra dell'uguaglianza abbia un certo segno ("più" o "meno"). Questa è, ad esempio, la funzione X peccato X, illimitato su entrambi i lati, non è infinitamente grande in .

Sotto sequenza UN N chiamato infinitamente grande, Se .

La funzione viene chiamata infinitamente grande in prossimità di un punto X 0 se .

La funzione viene chiamata infinitamente grande all'infinito, Se O .

Proprietà dell'infinitamente piccolo e dell'infinitamente grande

Confronto tra infinitesimi

Come confrontare quantità infinitesimali?
Il rapporto tra quantità infinitesimali costituisce la cosiddetta incertezza.

Definizioni

Supponiamo di avere valori infinitesimi α( X) e β( X) (o, cosa non importante ai fini della definizione, successioni infinitesimali).

Per calcolare tali limiti è conveniente utilizzare la regola di L'Hopital.

Esempi di confronto

Utilizzando DI-simbolismo, i risultati ottenuti possono essere scritti nella forma seguente X 5 = o(X 3). In questo caso sono vere le seguenti voci: 2X 2 + 6X = O(X) E X = O(2X 2 + 6X).

Valori equivalenti

Definizione

Se , allora si chiamano le quantità infinitesime α e β equivalente ().
È ovvio che le quantità equivalenti sono un caso speciale di quantità infinitesime dello stesso ordine di piccolezza.

Quando valgono le seguenti relazioni di equivalenza (come conseguenza dei cosiddetti limiti notevoli):

Teorema

Il limite del quoziente (rapporto) di due quantità infinitesime non cambierà se una di esse (o entrambe) viene sostituita da una quantità equivalente.

Questo teorema ha un significato pratico quando si trovano i limiti (vedi esempio).

Esempio di utilizzo

Sostituzione SioN 2X valore equivalente 2 X, noi abbiamo

Schizzo storico

Il concetto di “infinitesimale” veniva discusso già nell’antichità in relazione al concetto di atomi indivisibili, ma non era incluso nella matematica classica. Fu ripreso con l'avvento nel XVI secolo del “metodo degli indivisibili” che divideva la figura oggetto di studio in sezioni infinitesimali.

Nel XVII secolo ebbe luogo l'algebrizzazione del calcolo infinitesimale. Cominciarono a essere definiti come valori numerici, che sono minori di qualsiasi valore finito (diverso da zero) e tuttavia non sono uguali a zero. L'arte dell'analisi consisteva nel tracciare una relazione contenente degli infinitesimi (differenziali) e poi nell'integrarla.

I matematici della vecchia scuola mettono alla prova il concetto infinitesimale dura critica. Michel Rolle ha scritto che il nuovo calcolo è “ insieme di errori ingegnosi"; Voltaire osservò causticamente che il calcolo infinitesimale è l'arte di calcolare e misurare accuratamente cose la cui esistenza non può essere dimostrata. Perfino Huygens ammise di non comprendere il significato dei differenziali di ordine superiore.

Come ironia del destino, si può considerare l'emergere, a metà del secolo, dell'analisi non standard, che ha dimostrato che anche il punto di vista originale - gli infinitesimi reali - era coerente e poteva essere utilizzato come base per l'analisi.

Guarda anche

Fondazione Wikimedia. 2010.

Scopri cos'è la "quantità infinitesimale" in altri dizionari:

QUANTITÀ INFINITAMENTE PICCOLA- una quantità variabile in un certo processo, se in questo processo si avvicina (tende) infinitamente a zero... Grande Enciclopedia del Politecnico

Infinitesimale- ■ Qualcosa di sconosciuto, ma legato all'omeopatia... Lessico delle verità comuni