BESKONAČNO MALE FUNKCIJE I NJIHOVA GLAVNA SVOJSTVA

Funkcija y=f(x) pozvao infinitezimal at x→a ili kada x→∞ ako ili , tj. Infinitezimalna funkcija je funkcija čija je granica u datoj tački nula.

Primjeri.

Hajde da uspostavimo sledeću važnu relaciju:

Teorema. Ako je funkcija y=f(x) zastupljen na x→a kao zbir konstantnog broja b i beskonačno mali α(x): f(x)=b+ α(x) onda .

Obrnuto, ako , tada f(x)=b+α(x), gdje sjekira) je beskonačno mala pri x→a.

Dokaz.

Razmotrimo glavna svojstva infinitezimalnih funkcija.

Teorema 1. Algebarski zbir dva, tri i općenito bilo kojeg konačnog broja infinitezimala je infinitezimalna funkcija.

Dokaz. Dajemo dokaz za dva člana. Neka f(x)=α(x)+β(x), gdje i . Moramo dokazati da za proizvoljno mali ε > 0 tamo δ> 0, tako da za x zadovoljavanje nejednakosti |x – a|<δ , izvedeno |f(x)|< ε.

Pa da popravimo proizvoljan broj ε > 0. Pošto je, prema hipotezi teoreme, α(x) je infinitezimalna funkcija, onda postoji δ 1 > 0, koji u |x – a|< δ 1 imamo |α(x)|< ε / 2. Isto tako, pošto β(x) je beskonačno mala, onda postoji takvo δ 2 > 0, koji u |x – a|< δ 2 imamo | β(x)|< ε / 2.

Uzmimo δ=min(δ1 , δ2 } .Onda u susjedstvu točke a radijus δ svaka od nejednakosti će biti zadovoljena |α(x)|< ε / 2 i | β(x)|< ε / 2. Dakle, u ovom naselju će ih biti

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,

one. |f(x)|< ε, što je trebalo dokazati.

Teorema 2. Posao je beskonačan mala funkcija sjekira) za ograničenu funkciju f(x) at x→a(ili kada x→∞) je infinitezimalna funkcija.

Dokaz. Od funkcije f(x) je ograničen, onda postoji broj M tako da za sve vrijednosti x iz nekog susedstva tačke a|f(x)|≤M. Osim toga, pošto sjekira) je infinitezimalna funkcija za x→a, tada za proizvoljno ε > 0 postoji susjedstvo tačke a, u kojoj je nejednakost |α(x)|< ε /M. Zatim u manjem od ovih naselja koje imamo | αf|< ε /M= ε. A to znači to af- beskonačno mali. Za slučaj x→∞ dokaz se izvodi na sličan način.

Iz dokazane teoreme slijedi:

Posljedica 1. Ako i , onda .

Posljedica 2. Ako i c= const, zatim .

Teorema 3. Omjer infinitezimalne funkcije α(x) po funkciji f(x), čija je granica različita od nule, je infinitezimalna funkcija.

Dokaz. Neka . Zatim 1 /f(x) postoji ograničena funkcija. Dakle, razlomak je proizvod infinitezimalne funkcije i ograničene funkcije, tj. funkcija je beskonačno mala.

ODNOS IZMEĐU BESKONAČNO MALIH I BESKONAČNO VELIKIH FUNKCIJA

Teorema 1. Ako je funkcija f(x) je beskonačno velika pri x→a, zatim funkcija 1 /f(x) je beskonačno mala pri x→a.

Dokaz. Uzmite proizvoljan broj ε >0 i pokazati to nekima δ>0 (u zavisnosti od ε) za sve x, za koji |x – a|<δ , nejednakost je zadovoljena, a to će značiti da 1/f(x) je infinitezimalna funkcija. Zaista, pošto f(x) je beskonačno velika funkcija za x→a, onda postoji δ>0 tako da čim |x – a|<δ , pa | f(x)|> 1/ ε. Ali onda za isto x.

Primjeri.

Može se dokazati i suprotna teorema.

Teorema 2. Ako je funkcija f(x)- beskonačno mali u x→a(ili x→∞) i onda ne nestaje y= 1/f(x) je beskonačna funkcija.

Dokažite teoremu sami.

Primjeri.

Dakle, najjednostavnija svojstva beskonačno malih i beskonačno velikih funkcija mogu se napisati korištenjem sljedećih uvjetnih odnosa: A≠ 0

TEOREME O GRANICAMA

Teorema 1. Granica algebarskog zbira dvije, tri i općenito određenog broja funkcija jednaka je algebarskom zbiru granica ovih funkcija, tj.

Dokaz. Dokaz ćemo izvršiti za dva člana, jer se za bilo koji broj pojmova izvodi na isti način. Neka .Onda f(x)=b+α(x) i g(x)=c+β(x), gdje α i β su beskonačno male funkcije. shodno tome,

f(x) + g(x)=(b + c) + (α(x) + β(x)).

Jer b+c je konstanta, i α(x) + β(x) je onda infinitezimalna funkcija

Primjer. .

Teorema 2. Granica proizvoda dvije, tri i općenito konačnog broja funkcija jednaka je proizvodu granica ovih funkcija:

Dokaz. Neka . shodno tome, f(x)=b+α(x) i g(x)=c+β(x) i

fg = (b + α)(c + β) = bc + (bβ + cα + αβ).

Posao bc je konstantna vrijednost. Funkcija bβ + cα + αβ na osnovu svojstava infinitezimalnih funkcija, postoji infinitezimalna količina. Zbog toga .

Posljedica 1. Konstantni faktor se može izvaditi iz graničnog znaka:

.

Posljedica 2. Granica stepena je jednaka stepenu granice:

.

Primjer..

Teorema 3. Granica količnika dvije funkcije jednaka je količniku granica ovih funkcija ako je granica nazivnika različita od nule, tj.

.

Dokaz. Neka . shodno tome, f(x)=b+α(x) i g(x)=c+β(x), gdje α, β su beskonačno male. Uzmite u obzir količnik

Razlomak je beskonačno mala funkcija jer je brojnik beskonačno mala funkcija, a nazivnik ima ograničenje c2 ≠0.

Primjeri.

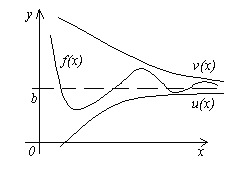
Teorema 4. Neka su date tri funkcije f(x), u(x) i v(x), zadovoljavajući nejednakosti u (x)≤f(x)≤v(x). Ako funkcije u(x) i v(x) imaju istu granicu x→a(ili x→∞), zatim funkciju f(x) teži istoj granici, tj. ako

, zatim .

Značenje ove teoreme jasno je iz slike.

Dokaz teoreme 4 može se naći, na primjer, u udžbeniku: Piskunov N. S. Diferencijalni i integralni račun, tom 1 - M.: Nauka, 1985.

Teorema 5. Ako na x→a(ili x→∞) funkcija y=f(x) uzima nenegativne vrijednosti y≥0 i teži krajnjim granicama b, tada ova granica ne može biti negativna: b≥0.

Dokaz. Dokaz će biti izveden kontradikcijom. Pretvarajmo se to b<0 , onda |y – b|≥|b| i, prema tome, modul razlike ne teži nuli na x→a. Ali onda y ne ide do krajnjih granica b at x→a, što je u suprotnosti sa uslovom teoreme.

Teorema 6. Ako dvije funkcije f(x) i g(x) za sve vrijednosti argumenta x zadovoljiti nejednakost f(x)≥ g(x) i imaju granice , onda imamo nejednakost b≥c.

Dokaz. Prema teoremi f(x)-g(x) ≥0, dakle, prema teoremi 5 , ili .

JEDNOSTRANE OGRANIČENJA

Do sada smo razmatrali definiciju granice funkcije kada x→a proizvoljno, tj. granica funkcije nije ovisila o tome kako je x prema a, lijevo ili desno od a. Međutim, prilično je uobičajeno pronaći funkcije koje nemaju ograničenja pod ovim uvjetom, ali imaju ograničenje ako x→a, ostajući na jednoj strani a, lijevo ili desno (vidi sl.). Stoga se uvodi koncept jednostranih granica.

Ako a f(x) teži krajnjim granicama b at x težeći nekom broju a tako x uzima samo vrijednosti manje od a, zatim pišite i pozovite kraj funkcije f(x) u tački a na lijevoj strani.

Funkcija y=f(x) pozvao infinitezimal at x→a ili kada x→∞ ako ili , tj. Infinitezimalna funkcija je funkcija čija je granica u datoj tački nula.

Primjeri.

1. Funkcija f(x)=(x-1) 2 je beskonačno malo za x→1, budući da (vidi sliku).

2. Funkcija f(x)=tg x je beskonačno mala pri x→0.

3. f(x)= log(1+ x) je beskonačno mala pri x→0.

4. f(x) = 1/x je beskonačno mala pri x→∞.

Hajde da uspostavimo sledeću važnu relaciju:

Teorema. Ako je funkcija y=f(x) zastupljen na x→a kao zbir konstantnog broja b i beskonačno mali α(x): f(x)=b+ α(x) onda .

Obrnuto, ako , tada f(x)=b+α(x), gdje sjekira) je beskonačno mala pri x→a.

Dokaz.

1. Dokažimo prvi dio tvrdnje. Od jednakosti f(x)=b+α(x) trebalo bi |f(x) – b|=| α|. Ali pošto sjekira) je beskonačno mala, onda za proizvoljno ε postoji δ, susjedstvo tačke a, za sve x od kojih, vrednosti sjekira) zadovoljiti odnos |α(x)|< ε. Onda |f(x) – b|< ε. A to znači da .

2. Ako , tada za bilo koje ε >0 za sve X iz nekog δ je susjedstvo tačke a bice |f(x) – b|< ε. Ali ako označimo f(x) – b= α, onda |α(x)|< ε, što znači da a- beskonačno mali.

Razmotrimo glavna svojstva infinitezimalnih funkcija.

Teorema 1. Algebarski zbir dva, tri i općenito bilo kojeg konačnog broja infinitezimala je infinitezimalna funkcija.

Dokaz. Dajemo dokaz za dva člana. Neka f(x)=α(x)+β(x), gdje i . Moramo dokazati da za proizvoljno mali ε > 0 tamo δ> 0, tako da za x zadovoljavanje nejednakosti |x – a|<δ , izvedeno |f(x)|< ε.

Dakle, fiksiramo proizvoljan broj ε > 0. Pošto je, prema hipotezi teoreme, α(x) je infinitezimalna funkcija, onda postoji δ 1 > 0, koji u |x – a|< δ 1 imamo |α(x)|< ε / 2. Isto tako, pošto β(x) je beskonačno mala, onda postoji takvo δ 2 > 0, koji u |x – a|< δ 2 imamo | β(x)|< ε / 2.

Uzmimo δ=min(δ1 , δ2 } .Onda u susjedstvu točke a radijus δ svaka od nejednakosti će biti zadovoljena |α(x)|< ε / 2 i | β(x)|< ε / 2. Dakle, u ovom naselju će ih biti

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,

one. |f(x)|< ε, što je trebalo dokazati.

Teorema 2. Proizvod infinitezimalne funkcije sjekira) za ograničenu funkciju f(x) at x→a(ili kada x→∞) je infinitezimalna funkcija.

Dokaz. Od funkcije f(x) je ograničen, onda postoji broj M tako da za sve vrijednosti x iz nekog susedstva tačke a|f(x)|≤M. Osim toga, pošto sjekira) je infinitezimalna funkcija za x→a, tada za proizvoljno ε > 0 postoji susjedstvo tačke a, u kojoj je nejednakost |α(x)|< ε /M. Zatim u manjem od ovih naselja koje imamo | αf|< ε /M= ε. A to znači to af- beskonačno mali. Za slučaj x→∞ dokaz se izvodi na sličan način.

Iz dokazane teoreme slijedi:

Posljedica 1. Ako i , onda .

Posljedica 2. Ako i c= const, zatim .

Teorema 3. Omjer infinitezimalne funkcije α(x) po funkciji f(x), čija je granica različita od nule, je infinitezimalna funkcija.

Dokaz. Neka . Zatim 1 /f(x) postoji ograničena funkcija. Dakle, razlomak je proizvod infinitezimalne funkcije i ograničene funkcije, tj. funkcija je beskonačno mala.

Definicija numerička funkcija. Načini postavljanja funkcija.

Neka je D skup na realnoj pravoj R. Ako je svakom x koji pripada D dodijeljen jedan broj y=f(x), onda kažemo da je funkcija f data.

Načini postavljanja funkcija:

1) tabelarni - za funkcije definisane na konačnom skupu.

2) analitičke

3) grafički

2 i 3 - za funkcije definirane na beskonačnom skupu.

Koncept inverzne funkcije.

Ako je funkcija y=f(x) takva da odgovaraju različite vrijednosti argumenta x različita značenja funkcija, tada se varijabla x može izraziti kao funkcija varijable y: x=g(y). Funkcija g naziva se inverznom od f i označava se sa f^(-1).

Koncept kompleksne funkcije.

Kompleks funkcija - funkcija, čiji je argument bilo koja druga funkcija.

Neka su date funkcije f(x) i g(x). Napravimo od njih dvije složene funkcije. S obzirom da je funkcija f eksterna (glavna), a funkcija g interna, dobijamo složena funkcija u(x)=f(g(x)).

Određivanje granice niza.

Broj a naziva se granica niza (xn) ako za bilo koji pozitivan broj postoji broj n0, počevši od kojeg se svi članovi posljednjeg razlikuju od a po modulu manjem od ε (tj. padaju u ε - susjedstvo tačke a):

Pravila za izračunavanje granica konvergentnih nizova.

1. Svaki konvergentni niz ima samo jednu granicu. 2. Ako su svi elementi niza (x n) jednaki C (konstanta), onda je i granica niza (x n) jednaka C. 3. ; 4. ; 5. .

Definicija ograničenog niza.

Niz (x n ) se naziva ograničenim ako je skup brojeva X=(x n ) ograničen: .

Definicija infinitezimalnog niza.

Niz (x n ) se naziva infinitezimalnim ako za bilo koji (proizvoljno mali) >0 postoji takav broj n 0 da je za bilo koji n>n 0 nejednakost |x n |< .

Definicija beskonačno velikog niza.

Niz se naziva beskonačno velikim ako za bilo koji (proizvoljno veliki) broj A>0 postoji takav broj n 0 da je za bilo koji broj n>n 0 nejednakost |x n |> A zadovoljena.

Definicija monotonih nizova.

Monotone sekvence: 1) povećanje ako je x n x n +1 za sve n, 4) nerastući ako je x n x n +1 za sve n.

Određivanje granice funkcije u tački.

Granica f-ii y \u003d f (x) u tački x 0 (ili u x x 0) je broj a, ako za bilo koju posljednju (x n) vrijednost argumenta konvergira na x 0 ( sve x n x 0), niz (f(x n)) vrijednosti f-ii konvergira do granice a.

Definicija infinitezimalne funkcije.

funkcija f(x) se naziva beskonačno malim za x→A ako je .

Definicija je beskonačna odlična funkcija.

funkcija f(x) se naziva beskonačno velikim u x→A ako je .

Def.: Funkcija se poziva infinitezimal u , ako .

U notaciji " ", pretpostavićemo da x0 može uzeti kao konačnu vrijednost: x0= Konst, i beskonačno: x0= ∞.

Svojstva infinitezimalnih funkcija:

1) Algebarski zbir konačnog broja beskonačno malih funkcija je beskonačno mali za funkciju.

2) Proizvod konačnog broja beskonačno malih funkcija je beskonačno mali za funkciju.

3) Umetničko delo ograničena funkcija na infinitezimalnu funkciju je infinitezimalna funkcija.

4) Kvocijent dijeljenja beskonačno male funkcije na funkciji čija je granica različita od nule je beskonačno mali na funkciji.

Primjer: Funkcija y = 2 + x je beskonačno malo na , jer .

Def.: Funkcija se poziva beskonačno velika u , ako .

Svojstva beskonačno velikih funkcija:

1) Zbir beskonačno velikih funkcija je beskonačno velik za funkciju.

2) Proizvod beskonačno velikog za funkciju na funkciju čija je granica različita od nule je beskonačno veliki za funkciju.

3) Zbir beskonačno velike funkcije i ograničene funkcije je beskonačno velika funkcija.

4) Kvocijent dijeljenja beskonačno velikog za funkciju sa funkcijom koja ima konačan limit je beskonačno veliki za funkciju.

Primjer: Funkcija y= je beskonačno velika za , jer .

Teorema.Odnos između beskonačno malih i beskonačno velikih količina. Ako je funkcija beskonačno mala na , tada je funkcija beskonačno velika na . Obrnuto, ako je funkcija beskonačno velika na , tada je funkcija beskonačno mala na .

Omjer dva beskonačno mala obično se označava simbolom, dva beskonačno velika - simbolom. Obje relacije su neodređene u smislu da njihova granica može postojati ili ne mora biti, biti jednaka određenom broju ili biti beskonačna, ovisno o vrsti specifičnih funkcija uključenih u neodređene izraze.

Pored neodređenih oblika i neodređenih su sljedeći izrazi:

Razlika beskonačno velikih istog znaka;

Proizvod beskonačno malog sa beskonačno velikim;

Funkcija eksponencijalne snage, čija baza teži 1, a indikator - ka;

Funkcija eksponencijalne snage, čija je baza beskonačno mala, a eksponent beskonačno velik;

Eksponencijalna funkcija čija su baza i eksponent beskonačno mali;

Eksponencijalna funkcija čija je baza beskonačno velika, a eksponent beskonačno mali.

Rečeno je da postoji nesigurnost odgovarajuće vrste. U tim slučajevima se poziva obračun limita otkrivanje neizvjesnosti. Da bi se otkrila nesigurnost, izraz pod predznakom granice se pretvara u oblik koji ne sadrži nesigurnost.

Prilikom izračunavanja granica koriste se svojstva granica, kao i svojstva infinitezimalnih i beskonačno velikih funkcija.

Razmotrimo primjere izračunavanja različitih granica.

1) . 2) .

4) , jer proizvod infinitezimalne funkcije na ograničenom funkcijom je beskonačno mali.

5) . 6) .

7) = =

. U ovom slučaju je postojala neodređenost tipa, koja je riješena faktoringom polinoma i redukcijom zajedničkim faktorom.

= .

U ovom slučaju je postojala neodređenost tipa , koja je riješena množenjem brojnika i nazivnika izrazom , korištenjem formule , a zatim smanjenjem razlomaka za (+1).

9)
. U ovom primjeru, nesigurnost tipa otkrivena je dijeljenjem brojnika i nazivnika razlomka po članu po najvišem stepenu.

Izvanredne granice

Prva divna granica : .

Dokaz. Razmotrimo jedinični krug (slika 3).

Fig.3. jedinični krug

Neka X je radijanska mjera centralnog ugla MOA(), onda OA = R= 1, MK= grijeh x, AT=tg x. Poređenje površina trouglova OMA, OTA i sektori OMA, dobijamo:

,

.

Podijelite posljednju nejednakost sa grijehom x, dobijamo:

.

Budući da je za , tada po svojstvu 5) granica

Odakle i recipročna vrijednost na , što je trebalo dokazati.

komentar: Ako je funkcija infinitezimalna na , tj. , tada prva izuzetna granica ima oblik:

.

Razmotrite primjere izračunavanja ograničenja koristeći prvu izvanrednu granicu.

Prilikom izračunavanja ove granice koristili smo se trigonometrijska formula: .

.

Razmotrite primjere izračunavanja ograničenja koristeći drugu izvanrednu granicu.

2) .

3) . Postoji vrsta dvosmislenosti. Onda napravimo zamjenu; u .

Račun beskonačno malih i velikih

Infinitezimalni račun- proračuni izvedeni sa infinitezimalnim vrijednostima, u kojima se izvedeni rezultat smatra beskonačnim zbirom infinitezimalnih. Infinitezimalni račun je opšti koncept za diferencijalni i integralni račun, koji čine osnovu moderne više matematike. Koncept beskonačno male količine usko je povezan s konceptom granice.

Infinitezimal

Subsequence a n pozvao infinitezimal, ako . Na primjer, niz brojeva je beskonačno mali.

Funkcija se poziva beskonačno mali u okolini tačke x 0 ako .

Funkcija se poziva beskonačno mali u beskonačnosti, ako ili .

Također beskonačno mala je funkcija koja je razlika između funkcije i njene granice, odnosno ako , onda f(x) − a = α( x) , .

beskonačno velika

U svim formulama ispod, beskonačnost desno od jednakosti implicira određeni znak (bilo "plus" ili "minus"). To je, na primjer, funkcija x grijeh x, neograničeno na obje strane, nije beskonačno velika za .

Subsequence a n pozvao beskonačno velika, ako .

Funkcija se poziva beskonačno velika u blizini tačke x 0 ako .

Funkcija se poziva beskonačno veliko u beskonačnosti, ako ili .

Svojstva infinitezimala i infinitezimala

Poređenje infinitezimala

Kako uporediti beskonačno male količine?
Odnos beskonačno malih veličina formira takozvanu nesigurnost.

Definicije

Pretpostavimo da imamo beskonačno mali za istu vrijednost α( x) i β( x) (ili, što nije važno za definiciju, infinitezimalni nizovi).

Za izračunavanje takvih granica zgodno je koristiti L'Hospitalovo pravilo.

Primeri poređenja

Koristeći O-simboli dobijenih rezultata mogu se napisati u sljedećem obliku x 5 = o(x 3). U ovom slučaju, unosi 2x 2 + 6x = O(x) i x = O(2x 2 + 6x).

Ekvivalentne količine

Definicija

Ako je , tada se nazivaju beskonačno male veličine α i β ekvivalentno ().
Očigledno, ekvivalentne veličine su poseban slučaj beskonačno malih količina istog reda male veličine.

Za , vrijede sljedeće relacije ekvivalencije (kao posljedica takozvanih izuzetnih granica):

Teorema

Ograničenje količnika (omjera) dvije infinitezimalne veličine neće se promijeniti ako se jedna od njih (ili obje) zamijeni ekvivalentnom vrijednošću.

Ova teorema je od praktične važnosti za pronalaženje granica (vidi primjer).

Primjer upotrebe

Zamjena sin 2x ekvivalentna vrijednost 2 x, dobijamo

Istorijski pregled

Koncept "beskonačno malog" raspravljao se u antičko doba u vezi s konceptom nedjeljivih atoma, ali nije ušao u klasičnu matematiku. Ponovo je oživljen pojavom u 16. veku "metode nedeljivih" - podele proučavane figure na beskonačno male delove.

Algebraizacija infinitezimalnog računa dogodila se u 17. veku. Oni su postali definisani kao numeričke vrijednosti, koji su manji od bilo koje konačne (ne-nulte) vrijednosti, a ipak nisu jednaki nuli. Umjetnost analize sastojala se u izradi relacije koja sadrži infinitezimale (diferencijale), a zatim u njenoj integraciji.

Matematičari stare škole su podvrgli koncept infinitezimal oštre kritike. Michel Rolle je napisao da je novi račun " skup briljantnih grešaka»; Voltaire je otrovno istakao da je ovaj račun umjetnost izračunavanja i preciznog mjerenja stvari čije postojanje nije moguće dokazati. Čak je i Hajgens priznao da ne razume značenje diferencijala višeg reda.

Kao ironiju sudbine može se uzeti u obzir pojava nestandardne analize sredinom veka, koja je dokazala da je prvobitna tačka gledišta – stvarne infinitezimale – takođe konzistentna i da se može uzeti kao osnova za analizu.

vidi takođe

Wikimedia fondacija. 2010 .

Pogledajte šta je "Infinitezimal" u drugim rječnicima:

BESKRAJNO MALE- varijabla u nekom procesu, ako se u ovom procesu beskonačno približava (teži) nuli... Velika politehnička enciklopedija

infinitezimal- ■ Nešto nepoznato, ali vezano za homeopatiju... Leksikon zajedničkih istina