Definizione. equazione caratteristica operatore lineare f è un'equazione della forma , dove λ è qualsiasi numero reale, А è la matrice dell'operatore lineare, Е è la matrice identità dello stesso ordine.
Polinomio chiamata polinomio caratteristico matrice A (operatore lineare f). In forma matriciale, l'equazione caratteristica ha la seguente forma:
o
.
Pertanto, eguagliando il polinomio caratteristico a zero, otteniamo un'equazione di grado n, dove λ agisce come un'incognita, otteniamo i valori delle sue radici - i numeri caratteristici di questa matrice. Le radici caratteristiche giocano un ruolo importante in molti rami della matematica. Considera una delle applicazioni delle radici caratteristiche - uno strumento molto importante nello studio spazi lineari, oltre a risolvere molti problemi applicati di algebra lineare.
L'insieme di tutte le radici dell'equazione caratteristica è chiamato spettro dell'operatore F(ogni radice è considerata con la molteplicità che ha nell'equazione caratteristica).
Esempio. Trova le radici caratteristiche della matrice.
Facciamo una matrice
Uguagliando il polinomio caratteristico a zero, otteniamo equazione quadrata
Allora ci sono le radici dell'equazione 
.
Definizione. Sia f un operatore spaziale lineare e sia un vettore diverso da zero che soddisfi l'uguaglianza
dove è un numero reale. Quindi il vettore è chiamato autovettore dell'operatore e matrice della sua definizione, - autovalore o autovalore della trasformazione. In questo caso, si dice che l'autovettore si riferisce all'autovalore .
Gli autovettori svolgono un ruolo importante, sia nella matematica stessa che nelle sue applicazioni. Ad esempio, una risonanza alla quale le frequenze naturali delle oscillazioni del sistema coincidono con la frequenza delle oscillazioni forze esterne. In matematica, gli autovettori sono utili nella risoluzione dei sistemi equazioni differenziali.
Teorema. Se l'operatore lineare f nella base (prima base) ha la matrice A e nella base (seconda base) - matrice B, allora avviene l'uguaglianza: .
Di conseguenza, passando ad una nuova base, il polinomio caratteristico dell'operatore lineare non cambia.
◌ Se T è la matrice di transizione dalla prima base alla seconda, allora . Quindi trasformiamo il lato destro dell'uguaglianza ●
Teorema. Affinché il numero λ 0 del campo Р sia un autovalore del vettore dello spazio L n su Р è necessario e sufficiente che il numero λ 0 sia la radice caratteristica dell'operatore f.
doc. IO. Necessitano. Lascia stare λ 0 autovalore dell'operatore F, poi dentro L n esiste un autovettore tale che .
Lascia stare 
è la sua stringa di coordinate in qualche modo, quindi
D'altra parte, poiché , dove è la matrice dell'operatore lineare nella base data, allora
Uguagliando le parti giuste di (1) e (2) otteniamo:
(3)
Uguaglianze (3) significano che il vettore numerico con le coordinate 
è una soluzione del seguente sistema di equazioni (4).
(4)
Il vettore è diverso da zero (perché è corretto), quindi il sistema (4) ha una soluzione diversa da zero, quindi il suo determinante è 0.
(5)
e quindi il determinante trasposto è 0.
(6)
In questo modo, λ 0 è la radice dell'equazione caratteristica.
II. Adeguatezza. Lascia stare λ 0
è la radice caratteristica dell'operatore in alcune basi 
. Dimostriamolo λ 0
è un autovalore dell'operatore A.
Infatti, se λ 0 è la radice caratteristica, allora l'uguaglianza (6) vale, e quindi l'uguaglianza (5), il che significa che il sistema (4) ha soluzioni diverse da zero.
Scegliamo una soluzione diversa da zero del sistema (4): un vettore numerico 
. Allora valgono le uguaglianze (3).
Consideriamo un vettore , e l'uguaglianza (2) vale per esso e, in virtù della formula , l'uguaglianza (1) è vera, dove è la matrice dell'operatore nella base IN. Ciò implica l'uguaglianza, il che significa che il vettore è un autovettore dell'operatore, che corrisponde all'autovalore λ 0 . Questo è ciò che doveva essere dimostrato. Il teorema è stato dimostrato.
Commento. Per trovare autovalori operatore, è necessario comporre e risolvere l'equazione (5). Per trovare gli autovettori dell'operatore, è necessario comporre un sistema di equazioni (4) e trovare un insieme fondamentale di soluzioni per questo sistema.
Per controllare la correttezza del calcolo degli autovalori (possono essere coincidenti, complessi), vengono utilizzati due fatti:
1) 
, dove l'ultima somma della traccia della matrice è la somma degli elementi diagonali.
2) 
.
Esempio. Trova autovalori e autovettori 
.
Uguando a zero otteniamo . .
3) . , 
.
Sia una variabile libera, quindi otteniamo un vettore 
.
L'esercizio. Fai un controllo per il vettore.
.
L'equazione caratteristica ha la forma:
Per determinare il tipo di componente libera, è necessario comporre e risolvere l'equazione caratteristica: z(p) = 0. Per scrivere l'equazione caratteristica, è necessario tracciare un diagramma in cui tutte le sorgenti di EMF e di corrente devono essere sostituite dal proprio interno resistenza, e resistenza l'induttanza e la capacità, rispettivamente, prendono uguale a Pl e, quindi è necessario interrompere un qualsiasi ramo di questo circuito, annotare la sua resistenza iniziale rispetto ai punti di rottura, eguagliarla a zero, risolvere e determinare le radici p, se le radici si è rivelato essere un vero negativo, quindi il componente gratuito della funzione desiderata:
, dove m è il numero di radici dell'equazione;
Radici; -integrabile costante.
Se le radici dell'equazione del carattere si sono rivelate coniugate complesse, lo stato libero sarà simile a:
dov'è la frequenza vibrazioni libere;
La fase iniziale delle oscillazioni libere.
8. Tempo transitorio. Definizione praticamente t pp. Calcolo del tempo del processo di transizione.
Il tempo del processo di transizione dipende dal coefficiente di attenuazione Il reciproco di , è chiamato costante di tempo ed è tempo, durante cui il valore della componente libera del transitorio diminuirà di e=2,72 volte. Il valore dipende dal circuito e dai parametri, quindi per un circuito con una connessione seriale r e L = , e con una connessione seriale
95% fine del transitorio 3 .
Le curve delle componenti libere del processo transitorio sono più facili da costruire impostando il tempo t sui valori 0, ,2 ..... Se ci sono più radici reali, allora la curva risultante si ottiene sommando le ordinate dei singoli termini (Fig. 1.)
Immagine 1:
9.10, Processo transitorio in r, C - circuiti quando acceso a una sorgente di tensione costante. Analisi da effettuare con il metodo classico; dare espressioni analitiche per U C (t); io C (t); grafici. (Metodo classico).
L'equazione di stato del circuito RC dopo la commutazione è la seguente:
(1) o rC (2)
La sua soluzione: 
La capacità C dopo la chiusura della chiave in t verrà caricata a valore fisso Componente libera
Poiché le condizioni iniziali sono zero, secondo la legge di commutazione 
a t=0, o 0=A , da cui A=-E.
La soluzione dell'equazione (2) assumerà la forma:
Corrente nel circuito i(t)=C
Immagine 1.
Figura 2.
I grafici della variazione di tensione e corrente i(t) sono mostrati nelle Figure 1 e 2. Dalle figure si può vedere che la tensione sul condensatore aumenta esponenzialmente da 0 a E, mentre l'intensità della corrente al momento della commutazione raggiunge bruscamente il valore E / r, quindi diminuisce a zero.
11.12 Processo transitorio nei circuiti r, C - quando collegato a una sorgente di tensione sinusoidale. Analisi da effettuare con il metodo classico; dare espressioni analitiche per U C (t); io C (t); grafici. (Metodo classico).
L'equazione di stato per un circuito rC in modalità transitoria è la seguente
rc 
.
Soluzione a questa equazione:
Componente gratuito
dove =rC
Poiché il circuito è lineare, quindi con azione sinusoidale e allo stato stazionario, anche la tensione sulla capacità varierà secondo una legge sinusoidale con la frequenza dell'azione in ingresso, Pertanto, per determinare =, utilizzeremo il metodo di ampiezze complesse:
; 
Dato che j= , otteniamo:
Costante di integrazione A della componente libera
Trova da condizioni iniziali nel circuito, tenendo conto della legge di commutazione:
.Quando t=0, l'ultima espressione ha la forma
Da dove viene A=-
Sommando i componenti e , otteniamo l'espressione finale per la tensione ai capi della capacità nella modalità transitoria:
= + = 
- (1)
L'analisi dell'espressione (1) mostra che il processo transitorio nel circuito rC sotto azione sinusoidale dipende dalla fase iniziale dell'EMF della sorgente al momento della commutazione e dalla costante di tempo del circuito rC.
Se , allora = 0 e nel circuito subito dopo la commutazione, si verificherà uno stato stazionario, cioè
Quando la tensione \u003d -, cioè la tensione sulla capacità subito dopo la commutazione può raggiungere quasi il doppio del valore del segno positivo, per poi avvicinarsi gradualmente a = .
La differenza di fase porterà l'equazione (1) nella forma:
La differenza tra questa modalità e la precedente è che la tensione sulla capacità subito dopo la commutazione può raggiungere quasi il doppio del segno negativo.
Per il circuito Rc considerato con una sorgente di corrente sinusoidale in regime stazionario, la fase iniziale della tensione di ingresso non ha alcun ruolo, ma la sua influenza è significativa nel processo transitorio.
13. Processo transitorio nei circuiti r, L, C - quando collegato a una sorgente di tensione costante. processo periodico. Espressioni analitiche per i(t), grafici. (Metodo classico).
Le radici sono reali, negative, diverse.
I(t)=Ho impostato +A1e p 1 t +A2e p 2 t
Processo periodico:
t=0 (i(0)=A1+A2; A1=-A2
{ 
t=0 i l (0)*r+L +Uc(0)=MI LA1=-LA2= ()
io l (t)= ( 
)
14. Processo transitorio nei circuiti r, L, C - quando collegato a una sorgente di tensione costante. processo critico. Espressioni analitiche per i(t), grafici. (Metodo classico).
io l (t)=io set +(B1+B2*t)*
t=0: io l (0)=β1=0
Se le radici si sono rivelate reali, negative, uguali, il processo è fondamentale.
15. Processo transitorio nei circuiti r, L, C quando collegato a una sorgente di tensione costante. processo oscillatorio. Espressione analitica per i(t), grafica. (Metodo classico).
P t = -δ±j*ω sv ω sv=
Le radici sono coniugate reali negative, in parte complesse.
i l (t)=i set A1e - δt *sin(ω st t+ψ)
i l (t)=i set +(M*cos ω St t+N*sin ω St t)*
io l (t)= * 
= *
16. Processo transitorio nei circuiti r, L, C quando collegato a una sorgente di tensione sinusoidale. processo aperiodico. Espressione analitica per i(t), grafica. (Metodo classico).
R(t)=Emax *sin(ωt+ψ)
2. 
Nel caso classico, il numero di equazioni in questo caso è uguale al numero di rami del circuito
Il metodo trova una soluzione nella forma della somma di una soluzione generale e una particolare. Il calcolo del processo transitorio è descritto da un sistema di equazioni differenziali ordinarie, compilato da uno dei metodi di calcolo per i valori istantanei delle funzioni temporali. La soluzione per ogni variabile di questo sistema si trova come somma delle soluzioni generali e particolari. Per compilare l'equazione è possibile utilizzare: un metodo basato sull'applicazione delle leggi di Kirchhoff, il metodo dei potenziali nodali, il metodo delle correnti di anello, ecc. Ad esempio, il sistema di equazioni differenziali, compilato dopo il passaggio secondo la prima e la seconda legge di Kirchhoff, ha la forma:
Per esempio,
Il numero di equazioni in questo caso è uguale al numero di rami del circuito. Sia richiesto di trovare la corrente i k nel ramo con il numero K. Eliminando le correnti dei rami in serie, si ottiene la corrente i k e le sue derivate fino all'ordine n:
L'ordine dell'equazione differenziale n è determinato dal numero di elementi del circuito reattivi indipendenti (m). Solitamente n=m, ma a seconda del metodo di connessione può essere che n Gli elementi capacitivi collegati in serie possono essere sostituiti da un elemento, così come gli elementi induttivi collegati in parallelo possono essere sostituiti da un elemento equivalente. La Figura 9.5 mostra la sostituzione di 2 serbatoi in serie con uno equivalente. Nel caso generale, l'ordine dell'equazione differenziale n è: n=n lc -n ce -n lj , dove n lc è il numero di elementi reattivi (L e C) nel circuito, n ce è il numero di capacitivi circuiti, n lj è il numero di nodi o sezioni induttivi. Capacitivo è inteso come un circuito costituito da elementi capacitivi o elementi capacitivi e sorgenti ideali di EMF, Fig. 9.6.a. Induttivo è inteso come un nodo in cui convergono rami induttivi o rami induttivi e sorgenti di corrente (Fig. 9.6.b), o sezioni che attraversano solo rami induttivi o rami induttivi e sorgenti di corrente. Si noti che la fase di compilazione di un'equazione differenziale non è obbligatoria e la corrente o la tensione transitoria possono essere trovate senza compilare un'equazione. Come indicato, nel metodo classico per il calcolo dei processi transitori, risolvendo equazioni Una soluzione particolare descrive una modalità chiamata forzata. La soluzione di un'equazione omogenea (il lato destro è uguale a zero) descrive il processo in assenza di EMF esterni e fonti di corrente ed è chiamata libera. Di conseguenza, vengono considerate le correnti, le tensioni e gli oneri liberi e forzati. Pertanto, la corrente nel ramo con numero K è rappresentata come una somma. L'equazione caratteristica viene compilata per il circuito dopo la commutazione. Può essere ottenuto nei seguenti modi: Direttamente sulla base di un'equazione differenziale della forma (1.2), cioè escludendo dal sistema di equazioni che descrivono lo stato elettromagnetico del circuito in base alle leggi di Kirchhoff, tutte le incognite, tranne una, rispetto alla quale si scrive l'equazione; Utilizzando l'espressione per la resistenza di ingresso del circuito su una corrente sinusoidale; Basato sull'espressione del determinante principale. Secondo il primo metodo in 1.4.1, è stata ottenuta un'equazione differenziale rispetto alla tensione u C su un condensatore per serie r-L-C-catene (vedi fig. 1.6): sulla base della quale si scrive l'equazione caratteristica Si noti che, essendo il circuito lineare coperto da un unico processo transitorio, le radici dell'equazione caratteristica sono comuni a tutte le componenti libere delle tensioni e delle correnti dei rami circuitali, i cui parametri sono inclusi nell'equazione caratteristica . Pertanto, secondo il primo metodo di compilazione dell'equazione caratteristica, qualsiasi valore può essere scelto come grandezza rispetto alla quale è scritto. La compilazione dell'equazione caratteristica secondo il metodo della resistenza di ingresso è la seguente: 1. L'espressione per la resistenza di ingresso del circuito in corrente alternata è scritta in forma complessa; 2. Nell'espressione risultante jω viene sostituito dall'operatore R; 3. L'espressione risultante è impostata su zero. L'equazione coincide con quella caratteristica. Va sottolineato che la resistenza di ingresso può essere scritta rispetto al punto di interruzione di qualsiasi ramo del circuito. In questo caso, le fonti di energia sono escluse dal circuito e le loro resistenze interne rimangono al loro posto. Questo metodo di compilazione dell'equazione caratteristica presuppone l'assenza di rami accoppiati magneticamente nel circuito elettrico. Se ce ne sono, è necessario effettuare un disaccoppiamento magnetico. Per il circuito in esame (vedi Fig. 1.6), secondo il metodo della resistenza di ingresso, si ha: Quando si compila un'equazione caratteristica basata sull'espressione del determinante principale, il numero di equazioni algebriche in base alle quali è scritta è uguale al numero di componenti di corrente libera sconosciute. L'algebrazione del sistema originario di equazioni integro-differenziali, compilato, ad esempio, sulla base delle leggi di Kirchhoff o con il metodo delle correnti d'anello, viene effettuata sostituendo le operazioni di differenziazione e integrazione, rispettivamente, moltiplicando e dividendo per il operatore R. L'equazione caratteristica si ottiene uguagliando a zero il determinante scritto. Poiché l'espressione per il determinante principale non dipende dal lato destro del sistema di equazioni disomogenee, può essere compilata sulla base di un sistema di equazioni scritte per correnti totali. Per lo schema in esame (vedi Fig. 1.6) per la modalità libera abbiamo: Sostituendo la derivata e l'integrale nell'equazione, come accennato in precedenza, otteniamo l'equazione algebrica Dove arriviamo L'equazione caratteristica viene compilata per il circuito dopo la commutazione. Può essere ottenuto nei seguenti modi: Secondo il primo metodo, nella lezione precedente, è stata ottenuta un'equazione differenziale per la tensione ai capi del condensatore per un circuito RLC in serie, sulla base della quale viene scritta l'equazione caratteristica. Si noti che, essendo il circuito lineare coperto da un unico processo transitorio, le radici dell'equazione caratteristica sono comuni a tutte le componenti libere delle tensioni e delle correnti dei rami circuitali, i cui parametri sono inclusi nell'equazione caratteristica . Pertanto, secondo il primo metodo di compilazione dell'equazione caratteristica, una qualsiasi può essere scelta come variabile rispetto alla quale è scritta. L'applicazione del secondo e del terzo metodo per la compilazione dell'equazione caratteristica sarà considerata utilizzando l'esempio del circuito di Fig. uno. La compilazione dell'equazione caratteristica secondo il metodo della resistenza di ingresso è la seguente: viene registrata l'impedenza di ingresso del circuito in corrente alternata; jw è sostituito dall'operatore p; l'espressione risultante è impostata su zero. L'equazione corrisponde alla caratteristica. Va sottolineato che la resistenza di ingresso può essere scritta rispetto al punto di interruzione di qualsiasi ramo del circuito. In questo caso, la rete attiva a due terminali viene sostituita da una passiva, per analogia con il metodo del generatore equivalente. Questo metodo di compilazione dell'equazione caratteristica presuppone l'assenza di rami accoppiati magneticamente nel circuito; se ve ne sono, è necessario effettuare il loro scioglimento preliminare. Per il circuito di fig. 1 rispetto ai terminali sorgente Sostituendo jw con p e uguagliando l'espressione risultante a zero, scriviamo Quando si compila un'equazione caratteristica basata sull'espressione del determinante principale, il numero di equazioni algebriche in base alle quali è scritta è uguale al numero di componenti di corrente libera sconosciute. L'algebrazione del sistema originario di equazioni integro-differenziali, compilato, ad esempio, sulla base delle leggi di Kirchhoff o con il metodo delle correnti d'anello, viene effettuata sostituendo i simboli di differenziazione e integrazione, rispettivamente, con moltiplicazione e divisione per il operatore p. L'equazione caratteristica si ottiene uguagliando a zero il determinante scritto. Poiché l'espressione per il determinante principale non dipende dal lato destro del sistema di equazioni disomogenee, può essere compilata sulla base di un sistema di equazioni scritte per correnti totali. Per il circuito di fig. 1, il sistema di equazioni algebraizzato basato sul metodo delle correnti d'anello ha la forma Da qui l'espressione per il determinante principale di questo sistema Uguagliando D a zero, otteniamo un risultato simile a (1). Metodologia generale per il calcolo dei transitori con il metodo classico Nel caso generale, il metodo per calcolare i processi transitori con il metodo classico comprende i seguenti passaggi: Esempi di calcolo di processi transitori con il metodo classico 1. Transitori nel circuito R-L quando è collegato a una sorgente di tensione Tali processi hanno luogo, ad esempio, quando elettromagneti, trasformatori, motori elettrici, ecc. sono collegati a una fonte di alimentazione. Considera due casi: Secondo il metodo considerato per la corrente nel circuito in fig. 2 può essere scritto Equazione caratteristica da dove e tempo costante In questo modo, Sostituendo (4) e (5) nella relazione (3), scriviamo Secondo la prima legge di commutazione. Quindi Pertanto, la corrente nel circuito nel processo transitorio è descritta dall'equazione e la tensione sull'induttore - dall'espressione La forma qualitativa delle curve e corrispondenti alle soluzioni ottenute è mostrata in Fig. . 3. Con il secondo tipo di sorgente, la componente forzata viene calcolata con il metodo simbolico: L'espressione per la componente libera non dipende dal tipo di sorgente di tensione. Di conseguenza, Perché poi Così, finalmente otteniamo L'analisi dell'espressione risultante (6) mostra: Se è di entità significativa, la componente libera non diminuisce in modo significativo in mezzo periodo. In questo caso, il valore massimo della corrente transitoria può superare significativamente l'ampiezza della corrente in regime stazionario. Come si può vedere dalla figura. 4, dove Pertanto, per un circuito lineare, il valore massimo della corrente transitoria non può superare il doppio dell'ampiezza della corrente forzata: . Allo stesso modo per un circuito lineare con un condensatore: se al momento della commutazione la tensione forzata è uguale al suo valore di ampiezza e la costante di tempo del circuito è abbastanza grande, allora dopo circa metà del periodo la tensione sul condensatore raggiunge il suo valore massimo , che non può superare il doppio dell'ampiezza della tensione forzata: 2. Transitori quando l'induttore è scollegato dalla fonte di alimentazione Quando si apre la chiave nel circuito di fig. 5 è la componente forzata della corrente attraverso l'induttore. Equazione caratteristica dove Secondo la prima legge di commutazione Pertanto, l'espressione per la corrente nel modo transitorio e la tensione ai capi dell'induttore L'analisi (7) mostra che all'apertura di circuiti contenenti elementi induttivi possono verificarsi grandi sovratensioni che, senza l'adozione di misure speciali, possono danneggiare l'apparecchiatura. Infatti, a 3. Carica e scarica del condensatore Quando la chiave viene ruotata in posizione 1 (vedi Fig. 6), inizia il processo di carica del condensatore: Componente forzata della tensione ai capi del condensatore. Dall'equazione caratteristica la radice è determinata 
è rappresentato come la somma delle soluzioni generali e particolari.
.
;
;
.
.
o 
.
o .
.
.
(1)
. .
(5)
.
,
,
.
,
. .
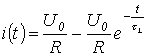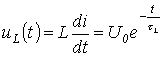(6)
, la corrente massima si verifica approssimativamente dopo . Nel limite di .
.
,
e 
.
.
.
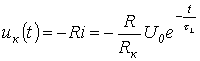(7)
il modulo di tensione sull'induttore al momento della commutazione sarà molte volte superiore alla tensione della sorgente: . In assenza di un resistore di spegnimento R, la tensione specificata viene applicata ai contatti di apertura della chiave, a seguito della quale si verifica un arco tra di loro.
.
. Da qui la costante di tempo.