Asosiy elementar funktsiyalar, ularga xos xususiyatlar va tegishli grafiklar matematik bilimlarning asoslaridan biri bo'lib, ko'paytirish jadvaliga o'xshash ahamiyatga ega. Elementar funktsiyalar barcha nazariy masalalarni o'rganish uchun asos, tayanchdir.

Quyidagi maqolada asosiy elementar funktsiyalar mavzusi bo'yicha asosiy materiallar keltirilgan. Biz atamalarni kiritamiz, ularga ta'riflar beramiz; Keling, elementar funktsiyalarning har bir turini batafsil o'rganamiz va ularning xususiyatlarini tahlil qilamiz.

Asosiy elementar funktsiyalarning quyidagi turlari ajratiladi:

Ta'rif 1

• doimiy funktsiya (doimiy);
• n-darajali ildiz;
• quvvat funktsiyasi;
• eksponensial funktsiya;
• logarifmik funktsiya;
• trigonometrik funktsiyalar;
• birodarlik trigonometrik funktsiyalari.

Doimiy funktsiya quyidagi formula bilan aniqlanadi: y = C (C - qandaydir haqiqiy son) va shuningdek, nomi bor: doimiy. Bu funktsiya x mustaqil o'zgaruvchining har qanday haqiqiy qiymati y o'zgaruvchining bir xil qiymatiga - C qiymatiga mos kelishini aniqlaydi.

Konstantaning grafigi x o'qiga parallel bo'lgan va koordinatalari (0, C) bo'lgan nuqtadan o'tadigan to'g'ri chiziqdir. Aniqlik uchun y = 5 , y = - 2 , y = 3 , y = 3 (chizmada mos ravishda qora, qizil va ko‘k ranglar bilan belgilangan) doimiy funksiyalarning grafiklarini keltiramiz.

Ta'rif 2

Bu elementar funksiya y = x n (n -) formulasi bilan aniqlanadi. natural son birdan ortiq).

Funktsiyaning ikkita variantini ko'rib chiqaylik.

1. n-darajali ildiz, n - juft son

Aniqlik uchun biz bunday funktsiyalarning grafiklarini ko'rsatadigan chizmani ko'rsatamiz: y = x , y = x 4 va y = x 8. Bu funksiyalar rangli kodlangan: mos ravishda qora, qizil va ko'k.

Indikatorning boshqa qiymatlari uchun teng darajali funktsiya grafiklarining o'xshash ko'rinishi.

Ta'rif 3

n-darajali funktsiya ildizining xossalari, n - juft son

• ta'rif sohasi barcha salbiy bo'lmaganlar to'plamidir haqiqiy raqamlar [ 0 , + ∞) ;
• x = 0 bo'lganda, funktsiya y = x n nolga teng qiymatga ega;
• bu funksiya funksiyadir umumiy ko'rinish(juft ham, toq ham emas);
• diapazon: [ 0 , + ∞);
• bu funktsiya y = x n ildizning teng darajalari bilan ta'rifning butun sohasi bo'ylab ortadi;
• funksiya butun ta'rif sohasi bo'yicha yuqoriga yo'naltirilgan qavariqga ega;
• hech qanday burilish nuqtalari yo'q;
• asimptotlar yo'q;
• juft n uchun funksiya grafigi (0 ; 0) va (1 ; 1) nuqtalardan oʻtadi.

1. n-darajali ildiz, n toq son

Bunday funktsiya butun haqiqiy sonlar to'plamida aniqlanadi. Aniqlik uchun funktsiyalar grafiklarini ko'rib chiqing y = x 3 , y = x 5 va x 9. Chizmada ular ranglar bilan ko'rsatilgan: mos ravishda egri chiziqlarning qora, qizil va ko'k ranglari.

y = x n funktsiya ildizining ko'rsatkichining boshqa g'alati qiymatlari shunga o'xshash shakldagi grafikni beradi.

Ta'rif 4

n-darajali funktsiya ildizining xossalari, n toq son

• ta'rif sohasi - barcha haqiqiy sonlar to'plami;
• bu funksiya g'alati;
• qiymatlar diapazoni - barcha haqiqiy raqamlar to'plami;
• ildizning toq darajali ko‘rsatkichlari bo‘lgan y = x n funksiya butun ta’rif sohasi bo‘yicha ortadi;
• funksiya (- ∞ ; 0 ] oraliqda konkavlikka va [ 0 , + ∞) intervalda qavariqlikka ega;
• burilish nuqtasi koordinatalariga ega (0 ; 0);
• asimptotlar yo'q;
• toq n uchun funksiya grafigi (- 1 ; - 1) , (0 ; 0) va (1 ; 1) nuqtalardan oʻtadi.

Quvvat funktsiyasi

Ta'rif 5

Quvvat funksiyasi y = x a formula bilan aniqlanadi.

Grafiklarning turi va funksiyaning xossalari ko'rsatkich qiymatiga bog'liq.

• daraja funksiyasi a butun ko‘rsatkichga ega bo‘lsa, daraja funksiyasi grafigining shakli va uning xossalari ko‘rsatkichning juft yoki toq ekanligiga, shuningdek, ko‘rsatkich qanday belgiga ega bo‘lishiga bog‘liq. Keling, ushbu barcha maxsus holatlarni quyida batafsil ko'rib chiqaylik;
• ko'rsatkich kasr yoki irratsional bo'lishi mumkin - shunga qarab, grafiklarning turi va funksiyaning xususiyatlari ham o'zgaradi. Biz bir nechta shartlarni o'rnatish orqali maxsus holatlarni tahlil qilamiz: 0< a < 1 ; a > 1 ; - 1 < a < 0 и a < - 1 ;
• quvvat funksiyasi nol ko'rsatkichga ega bo'lishi mumkin, biz bu holatni quyida batafsilroq tahlil qilamiz.

Keling, quvvat funksiyasini tahlil qilaylik a toq bo'lganda y = x a ijobiy raqam, masalan, a = 1 , 3 , 5 ...

Aniqlik uchun biz bunday quvvat funktsiyalarining grafiklarini ko'rsatamiz: y = x (grafikning qora rangi), y = x 3 (grafikning ko'k rangi), y = x 5 (grafikning qizil rangi), y = x 7 (yashil grafik). a = 1 bo'lganda, y = x chiziqli funktsiyani olamiz.

Ta'rif 6

Ko‘rsatkich toq musbat bo‘lganda quvvat funksiyasining xossalari

• funksiya x ∈ (- ∞ ; + ∞) uchun ortib bormoqda;
• funksiya x ∈ (- ∞ ; 0 ] uchun qavariq va x ∈ [ 0 ; + ∞) uchun botiq (chiziqli funksiya bundan mustasno);
• burilish nuqtasi koordinatalariga ega (0 ; 0) (chiziqli funktsiyadan tashqari);
• asimptotlar yo'q;
• funksiya o‘tish nuqtalari: (- 1 ; - 1) , (0 ; 0) , (1 ; 1) .

Keling, quvvat funksiyasini tahlil qilaylik y = x a agar a juft musbat son bo'lsa, masalan, a = 2 , 4 , 6 ...

Aniqlik uchun biz bunday quvvat funktsiyalarining grafiklarini ko'rsatamiz: y \u003d x 2 (grafikning qora rangi), y = x 4 (grafikning ko'k rangi), y = x 8 (grafikning qizil rangi). a = 2 bo'lganda, grafigi kvadratik parabola bo'lgan kvadrat funktsiyani olamiz.

Ta'rif 7

Ko‘rsatkich hatto musbat bo‘lganda quvvat funksiyasining xossalari:

• aniqlash sohasi: x ∈ (- ∞ ; + ∞) ;
• x ∈ uchun kamayuvchi (- ∞ ; 0 ] ;
• funksiya x ∈ (- ∞ ; + ∞) uchun botiq;
• hech qanday burilish nuqtalari yo'q;
• asimptotlar yo'q;
• funksiya o‘tish nuqtalari: (- 1 ; 1) , (0 ; 0) , (1 ; 1) .

Quyidagi rasmda eksponensial funktsiya grafiklarining misollari ko'rsatilgan y = x a toq manfiy son bo‘lganda: y = x - 9 (grafikning qora rangi); y = x - 5 (diagrammaning ko'k rangi); y = x - 3 (diagrammaning qizil rangi); y = x - 1 (yashil grafik). Agar \u003d - 1 bo'lsa, biz teskari proportsionallikni olamiz, uning grafigi giperbola.

Ta'rif 8

Ko'rsatkich g'alati manfiy bo'lganda quvvat funksiyasi xususiyatlari:

X \u003d 0 bo'lganda, biz ikkinchi turdagi uzilishni olamiz, chunki lim x → 0 - 0 x a \u003d - ∞, lim x → 0 + 0 x a \u003d + ∞ a \u003d - 1, - 3, - 5, .... Shunday qilib, x = 0 to'g'ri chiziq vertikal asimptotadir;

• diapazon: y ∈ (- ∞ ; 0) ∪ (0 ; + ∞) ;
• funksiya toq, chunki y (- x) = - y (x) ;
• funksiya x ∈ - ∞ uchun kamaymoqda; 0 ∪ (0 ; + ∞) ;
• funksiya x ∈ (- ∞ ; 0) uchun qavariq va x ∈ (0 ; + ∞) uchun botiq;
• hech qanday burilish nuqtalari yo'q;

k = lim x → ∞ x a x = 0 , b = lim x → ∞ (x a - k x) = 0 ⇒ y = k x + b = 0 bo'lganda a = - 1 , - 3 , - 5 , . . . .

• funksiya o‘tish nuqtalari: (- 1 ; - 1) , (1 ; 1) .

Quyidagi rasmda a juft manfiy son bo'lganda y = x a quvvat funksiyasi grafiklariga misollar ko'rsatilgan: y = x - 8 (qora rangdagi diagramma); y = x - 4 (grafikning ko'k rangi); y = x - 2 (grafikning qizil rangi).

Ta'rif 9

Ko'rsatkich hatto manfiy bo'lganda quvvat funksiyasi xususiyatlari:

• aniqlash sohasi: x ∈ (- ∞ ; 0) ∪ (0 ; + ∞) ;

X \u003d 0 bo'lganda, biz ikkinchi turdagi uzilishni olamiz, chunki lim x → 0 - 0 x a \u003d + ∞, lim x → 0 + 0 x a \u003d + ∞ a \u003d - 2, - 4, - 6, .... Shunday qilib, x = 0 to'g'ri chiziq vertikal asimptotadir;

• funksiya juft, chunki y (- x) = y (x) ;
• funksiya x ∈ (- ∞ ; 0) uchun ortib bormoqda va x ∈ 0 uchun kamaymoqda; +∞ ;
• funksiya x ∈ (- ∞ ; 0) ∪ (0 ; + ∞) uchun botiq;
• hech qanday burilish nuqtalari yo'q;
• gorizontal asimptota to'g'ri chiziq y = 0, chunki:

k = lim x → ∞ x a x = 0, b = lim x → ∞ (x a - k x) = 0 ⇒ y = k x + b = 0 bo'lganda, a = - 2 , - 4 , - 6 , . . . .

• funksiya o'tish nuqtalari: (- 1 ; 1) , (1 ; 1) .

Eng boshidanoq quyidagi jihatga e'tibor bering: a toq maxrajli musbat kasr bo'lsa, ba'zi mualliflar bu daraja funksiyasini aniqlash sohasi sifatida - ∞ oralig'ini oladilar; + ∞ , a ko'rsatkichining qaytarilmas kasr ekanligini ko'rsatadi. Hozirgi vaqtda algebra va tahlilning boshlanishi bo'yicha ko'plab o'quv nashrlari mualliflari quvvat funktsiyalari, bu erda ko'rsatkich argumentning salbiy qiymatlari uchun toq maxrajli kasrdir. Bundan tashqari, biz aynan shunday pozitsiyaga amal qilamiz: biz to'plamni olamiz [ 0 ; +∞). Talabalar uchun tavsiya: kelishmovchiliklarga yo'l qo'ymaslik uchun ushbu nuqtada o'qituvchining nuqtai nazarini bilib oling.

Shunday qilib, keling, quvvat funktsiyasini ko'rib chiqaylik ko'rsatkich ratsional yoki irratsional son bo'lganda y = x a 0 bo'lganda< a < 1 .

Keling, quvvat funktsiyalarini grafiklar bilan ko'rsatamiz y = x a qachon a = 11 12 (qora rangdagi diagramma); a = 5 7 (grafikning qizil rangi); a = 1 3 (grafikning ko'k rangi); a = 2 5 (grafikning yashil rangi).

a ko'rsatkichining boshqa qiymatlari (0 bo'lsa< a < 1) дадут аналогичный вид графика.

Ta'rif 10

0 da quvvat funksiyasi xususiyatlari< a < 1:

• diapazon: y ∈ [ 0 ; +∞);
• funksiya x ∈ [ 0 uchun ortib bormoqda; +∞);
• funksiya x ∈ (0 ; + ∞) uchun qavariqlikka ega;
• hech qanday burilish nuqtalari yo'q;
• asimptotlar yo'q;

Keling, quvvat funksiyasini tahlil qilaylik y = x a ko'rsatkich butun son bo'lmagan ratsional yoki irratsional son bo'lganda, a > 1 bo'lsa.

Biz quvvat funktsiyasining grafiklarini tasvirlaymiz y \u003d x a berilgan sharoitlarda quyidagi funktsiyalardan foydalanib misol sifatida: y \u003d x 5 4, y \u003d x 4 3, y \u003d x 7 3, y \u003d x 3 p (qora, qizil, ko'k, yashil mos ravishda grafiklar).

a > 1 shartidagi a ko‘rsatkichining boshqa qiymatlari grafikning xuddi shunday ko‘rinishini beradi.

Ta'rif 11

a > 1 uchun quvvat funksiyasi xususiyatlari:

• ta'rif sohasi: x ∈ [ 0 ; +∞);
• diapazon: y ∈ [ 0 ; +∞);
• bu funksiya umumiy shakl funksiyasi (toq ham, juft ham emas);
• funksiya x ∈ [ 0 uchun ortib bormoqda; +∞);
• funktsiya x ∈ (0 ; + ∞) uchun botiq bo'ladi (1 bo'lganda< a < 2) и выпуклость при x ∈ [ 0 ; + ∞) (когда a > 2);
• hech qanday burilish nuqtalari yo'q;
• asimptotlar yo'q;
• funksiya o'tish nuqtalari: (0 ; 0) , (1 ; 1) .

Sizning e'tiboringizni qaratamiz!a toq maxrajli manfiy kasr bo'lsa, ba'zi mualliflarning asarlarida bu holda ta'rif sohasi interval - ∞; 0 ∪ (0 ; + ∞) a ko‘rsatkichi qaytarilmas kasr bo‘lishi sharti bilan. Ayni paytda mualliflar o'quv materiallari algebra va tahlilning boshlanishiga ko'ra, argumentning manfiy qiymatlari bo'lgan g'alati maxrajli kasr ko'rinishidagi ko'rsatkichli quvvat funktsiyalari TA'RIQLANMAYDI. Bundan tashqari, biz aynan shunday ko'rinishga amal qilamiz: kasr manfiy ko'rsatkichlari bo'lgan quvvat funktsiyalari sohasi sifatida (0 ; + ∞) to'plamni olamiz. Talabalar uchun maslahat: kelishmovchilikni oldini olish uchun o'qituvchingizning nuqtai nazarini aniqlang.

Biz mavzuni davom ettiramiz va quvvat funktsiyasini tahlil qilamiz y = x a taqdim etilgan: - 1< a < 0 .

Bu erda grafiklar chizilgan keyingi xususiyatlar: y = x - 5 6 , y = x - 2 3 , y = x - 1 2 2 , y = x - 1 7 (mos ravishda qora, qizil, ko'k, yashil chiziqlar).

Ta'rif 12

Quvvat funksiyasi xususiyatlari - 1< a < 0:

lim x → 0 + 0 x a = + ∞ qachon - 1< a < 0 , т.е. х = 0 – вертикальная асимптота;

• diapazon: y ∈ 0 ; +∞ ;
• bu funksiya umumiy shakl funksiyasi (toq ham, juft ham emas);
• hech qanday burilish nuqtalari yo'q;

Quyidagi rasmda y = x - 5 4 , y = x - 5 3 , y = x - 6 , y = x - 24 7 (qora, qizil, ko'k, yashil ranglar mos ravishda egri chiziqlar).

Ta'rif 13

a uchun quvvat funksiyasi xususiyatlari< - 1:

• ta'rif sohasi: x ∈ 0 ; +∞ ;

lim x → 0 + 0 x a = + ∞ qachon a< - 1 , т.е. х = 0 – вертикальная асимптота;

• diapazon: y ∈ (0 ; + ∞) ;
• bu funksiya umumiy shakl funksiyasi (toq ham, juft ham emas);
• funksiya x ∈ 0 uchun kamayib bormoqda; +∞ ;
• funksiya x ∈ 0 uchun botiq; +∞ ;
• hech qanday burilish nuqtalari yo'q;
• gorizontal asimptota - to'g'ri chiziq y = 0;
• funktsiyaning o'tish nuqtasi: (1 ; 1) .

Agar \u003d 0 va x ≠ 0 bo'lsa, biz y \u003d x 0 \u003d 1 funktsiyasini olamiz, bu nuqta (0; 1) chiqarib tashlangan chiziqni aniqlaydi (biz 0 0 ifodasi berilmasligiga kelishib oldik) har qanday qiymat).

Eksponensial funktsiya shaklga ega y = a x, bu erda a > 0 va a ≠ 1 va bu funktsiyaning grafigi a asosining qiymatiga qarab har xil ko'rinadi. Keling, alohida holatlarni ko'rib chiqaylik.

Keling, avvalo, asos bo'lganda vaziyatni ko'rib chiqaylik eksponensial funktsiya noldan birgacha qiymatga ega (0< a < 1) . A = 1 2 (egri chiziqning ko'k rangi) va a = 5 6 (egri chiziqning qizil rangi) uchun funktsiyalar grafiklari tasviriy misoldir.

Eksponensial funktsiyaning grafiklari 0 bo'lsa, bazaning boshqa qiymatlari uchun xuddi shunday shaklga ega bo'ladi.< a < 1 .

Ta'rif 14

Bazasi birdan kichik bo'lganda ko'rsatkichli funktsiyaning xossalari:

• diapazon: y ∈ (0 ; + ∞) ;
• bu funksiya umumiy shakl funksiyasi (toq ham, juft ham emas);
• asosi birdan kichik bo'lgan eksponensial funktsiya butun ta'rif sohasi bo'ylab kamaymoqda;
• hech qanday burilish nuqtalari yo'q;
• gorizontal asimptota - x o'zgaruvchisi + ∞ ga moyil bo'lgan y = 0 to'g'ri chiziq;

Endi ko'rsatkichli funktsiyaning asosi birdan (a > 1) katta bo'lgan holatni ko'rib chiqing.

Ushbu maxsus holatni y = 3 2 x (egri chiziqning ko'k rangi) va y = e x (grafikning qizil rangi) ko'rsatkichli funktsiyalar grafigi bilan ko'rsatamiz.

Bazaning birdan katta boshqa qiymatlari eksponensial funktsiya grafigiga o'xshash ko'rinishni beradi.

Ta'rif 15

Baza birdan katta bo'lganda ko'rsatkichli funktsiyaning xususiyatlari:

• ta'rif sohasi haqiqiy sonlarning butun to'plamidir;
• diapazon: y ∈ (0 ; + ∞) ;
• bu funksiya umumiy shakl funksiyasi (toq ham, juft ham emas);
• asosi birdan katta bo'lgan ko'rsatkichli funksiya x ∈ - ∞ uchun ortib bormoqda; +∞ ;
• funksiya x ∈ - ∞ uchun botiq; +∞ ;
• hech qanday burilish nuqtalari yo'q;
• gorizontal asimptota - y = 0 to'g'ri chiziq x o'zgaruvchisi - ∞ ga moyil;
• funktsiyaning o'tish nuqtasi: (0 ; 1) .

Logarifmik funktsiya y = log a (x) ko'rinishga ega, bu erda a > 0, a ≠ 1 .

Bunday funktsiya faqat argumentning ijobiy qiymatlari uchun aniqlanadi: x ∈ 0 uchun; +∞ .

Logarifmik funktsiyaning grafigi a asosining qiymatidan kelib chiqqan holda boshqa shaklga ega.

Avval 0 bo'lgan vaziyatni ko'rib chiqing< a < 1 . Продемонстрируем этот частный случай графиком логарифмической функции при a = 1 2 (синий цвет кривой) и а = 5 6 (красный цвет кривой).

Bazaning bittadan katta bo'lmagan boshqa qiymatlari grafikning o'xshash ko'rinishini beradi.

Ta'rif 16

Logarifmik funktsiyaning asosi birdan kichik bo'lganda xossalari:

• ta'rif sohasi: x ∈ 0 ; +∞ . X o'ngdan nolga moyil bo'lgani uchun funksiya qiymatlari + ∞ ga intiladi;
• diapazon: y ∈ - ∞ ; +∞ ;
• bu funksiya umumiy shakl funksiyasi (toq ham, juft ham emas);
• logarifmik
• funksiya x ∈ 0 uchun botiq; +∞ ;
• hech qanday burilish nuqtalari yo'q;
• asimptotlar yo'q;

Endi logarifmik funktsiyaning asosi birdan katta bo'lgan maxsus holatni tahlil qilaylik: a > 1 . Quyidagi chizmada y = log 3 2 x va y = ln x logarifmik funksiyalarning grafiklari (mos ravishda grafiklarning ko'k va qizil ranglari) mavjud.

Birdan kattaroq bazaning boshqa qiymatlari grafikning o'xshash ko'rinishini beradi.

Ta'rif 17

Bazasi birdan katta bo‘lgan logarifmik funksiyaning xossalari:

• ta'rif sohasi: x ∈ 0 ; +∞ . X o'ngdan nolga moyil bo'lgani uchun funksiya qiymatlari - ∞ ga intiladi;
• diapazon: y ∈ - ∞ ; + ∞ (haqiqiy sonlarning butun to'plami);
• bu funksiya umumiy shakl funksiyasi (toq ham, juft ham emas);
• logarifmik funksiya x ∈ 0 uchun ortib bormoqda; +∞ ;
• funksiya x ∈ 0 uchun qavariqlikka ega; +∞ ;
• hech qanday burilish nuqtalari yo'q;
• asimptotlar yo'q;
• funktsiyaning o'tish nuqtasi: (1 ; 0) .

Trigonometrik funksiyalar sinus, kosinus, tangens va kotangensdir. Keling, ularning har birining xususiyatlarini va tegishli grafiklarni tahlil qilaylik.

Umuman olganda, barcha trigonometrik funktsiyalar davriylik xususiyati bilan tavsiflanadi, ya'ni. funksiya qiymatlari da takrorlanganda turli ma'nolar argument, bir-biridan f (x + T) = f (x) davrining qiymati bilan farqlanadi (T - davr). Shunday qilib, trigonometrik funktsiyalarning xossalari ro'yxatiga "eng kichik ijobiy davr" bandi qo'shiladi. Bundan tashqari, biz tegishli funktsiya yo'qolgan argumentning bunday qiymatlarini ko'rsatamiz.

1. Sinus funksiyasi: y = sin(x)

Ushbu funktsiyaning grafigi sinus to'lqin deb ataladi.

Ta'rif 18

Sinus funksiyasining xossalari:

• ta'rif sohasi: haqiqiy sonlarning butun to'plami x ∈ - ∞ ; +∞ ;
• funktsiya x = p k bo'lganda yo'qoladi, bu erda k ∈ Z (Z - butun sonlar to'plami);
• funksiya x ∈ - p 2 + 2 p · k uchun ortib bormoqda; p 2 + 2 p k, k ∈ Z va x ∈ p 2 + 2 p k uchun kamayuvchi; 3 p 2 + 2 p k, k ∈ Z;
• sinus funktsiyasi mavjud mahalliy maksimal p 2 + 2 p · k nuqtalarida; 1 va nuqtalarda mahalliy minimal - p 2 + 2 p · k ; - 1 , k ∈ Z ;
• x ∈ - p + 2 p k bo'lganda sinus funksiya botiq bo'ladi; 2 p k, k ∈ Z va x ∈ 2 p k bo'lganda qavariq; p + 2 p k , k ∈ Z ;
• asimptotlar yo'q.

1. kosinus funktsiyasi: y=cos(x)

Ushbu funktsiyaning grafigi kosinus to'lqini deb ataladi.

Ta'rif 19

Kosinus funksiyasining xossalari:

• ta'rif sohasi: x ∈ - ∞ ; +∞ ;
• eng kichik ijobiy davr: T \u003d 2 p;
• diapazon: y ∈ - 1 ; bitta;
• bu funksiya juft, chunki y (- x) = y (x) ;
• funksiya x ∈ - p + 2 p · k uchun ortib bormoqda; 2 p · k, k ∈ Z va x ∈ 2 p · k uchun kamayuvchi; p + 2 p k , k ∈ Z ;
• kosinus funksiyasi 2 p · k nuqtalarda mahalliy maksimallarga ega; 1, k ∈ Z va p + 2 p · k nuqtalarda mahalliy minimallar; - 1 , k ∈ z ;
• x ∈ p 2 + 2 p · k bo'lganda kosinus funktsiyasi konkav bo'ladi; 3 p 2 + 2 p k, k ∈ Z va x ∈ - p 2 + 2 p k bo'lganda qavariq; p 2 + 2 p · k, k ∈ Z;
• burilish nuqtalari koordinatalariga ega p 2 + p · k ; 0 , k ∈ Z
• asimptotlar yo'q.

1. Tangent funktsiyasi: y = t g (x)

Bu funksiyaning grafigi deyiladi tangentoid.

Ta'rif 20

Tangens funksiyaning xossalari:

• ta'rif sohasi: x ∈ - p 2 + p · k ; p 2 + p k , bu erda k ∈ Z (Z - butun sonlar to'plami);
• Tangens funksiyaning aniqlanish sohasi chegarasidagi xatti-harakati lim x → p 2 + p · k + 0 t g (x) = - ∞ , lim x → p 2 + p · k - 0 t g (x) = + ∞ . Shunday qilib, x = p 2 + p · k k ∈ Z chiziqlar vertikal asimptotadir;
• k ∈ Z uchun x = p k bo'lganda funktsiya yo'qoladi (Z - butun sonlar to'plami);
• diapazon: y ∈ - ∞ ; +∞ ;
• bu funksiya toq, chunki y (- x) = - y (x) ;
• funktsiya - p 2 + p · k da ortib bormoqda; p 2 + p k, k ∈ Z;
• tangens funksiyasi x ∈ [ p · k uchun konkavdir; p 2 + p k) , k ∈ Z va x ∈ uchun qavariq (- p 2 + p k ; p k ] , k ∈ Z ;
• burilish nuqtalari p k koordinatalariga ega; 0, k ∈ Z;

1. Kotangent funktsiyasi: y = c t g (x)

Bu funksiyaning grafigi kotangentoid deyiladi. .

Ta'rif 21

Kotangent funksiyaning xossalari:

• ta'rif sohasi: x ∈ (p k ; p + p k) , bu erda k ∈ Z (Z - butun sonlar to'plami);

Kotangent funksiyaning aniqlanish sohasi chegarasidagi harakati lim x → p · k + 0 t g (x) = + ∞ , lim x → p · k - 0 t g (x) = - ∞ . Shunday qilib, x = p k k ∈ Z chiziqlar vertikal asimptotadir;

• eng kichik ijobiy davr: T \u003d p;
• k ∈ Z uchun x = p 2 + p k bo'lganda funksiya yo'qoladi (Z - butun sonlar to'plami);
• diapazon: y ∈ - ∞ ; +∞ ;
• bu funksiya toq, chunki y (- x) = - y (x) ;
• funksiya x ∈ p · k uchun kamayib bormoqda; p + p k , k ∈ Z ;
• kotangent funksiyasi x ∈ (p k ; p 2 + p k ] , k ∈ Z va x ∈ [ - p 2 + p k ; p k ) uchun qavariq, k ∈ Z uchun botiq;
• burilish nuqtalari koordinatalariga ega p 2 + p · k ; 0, k ∈ Z;
• qiya va gorizontal asimptotlar mavjud emas.

Teskari trigonometrik funksiyalar arksinus, arkkosinus, arktangent va arkkotangentdir. Ko'pincha, nomda "ark" prefiksi mavjudligi sababli, teskari trigonometrik funktsiyalar yoy funktsiyalari deb ataladi. .

1. Arksinus funksiyasi: y = a r c sin (x)

Ta'rif 22

Arksinus funksiyasining xossalari:

• bu funksiya toq, chunki y (- x) = - y (x) ;
• arksinus funksiyasi x ∈ 0 uchun botiq; 1 va x ∈ - 1 uchun qavariq; 0;
• burilish nuqtalari koordinatalariga ega (0 ; 0) , u ham funktsiyaning noli;
• asimptotlar yo'q.

1. Arkkosin funktsiyasi: y = a r c cos (x)

Ta'rif 23

Arkkosin funktsiyasining xususiyatlari:

• ta'rif sohasi: x ∈ - 1 ; bitta;
• diapazon: y ∈ 0 ; p;
• bu funksiya umumiy shaklda (juft ham, toq ham emas);
• funksiya butun ta'rif sohasi bo'yicha kamayib bormoqda;
• arkkosinus funksiyasi x ∈ - 1 uchun konkav; 0 va x ∈ 0 uchun qavariqlik; bitta;
• burilish nuqtalari koordinatalariga ega 0 ; p2;
• asimptotlar yo'q.

1. Arktangens funksiya: y = a r c t g (x)

Ta'rif 24

Arktangent funktsiyasining xususiyatlari:

• ta'rif sohasi: x ∈ - ∞ ; +∞ ;
• diapazon: y ∈ - p 2 ; p2;
• bu funksiya toq, chunki y (- x) = - y (x) ;
• funksiya butun ta'rif sohasi bo'ylab ortib bormoqda;
• arktangens funksiya x ∈ (- ∞ ; 0 ] uchun botiq va x ∈ [ 0 ; + ∞) uchun qavariq;
• burilish nuqtasi koordinatalariga ega (0; 0), u ham funktsiyaning noli;
• gorizontal asimptotlar x → - ∞ uchun y = - p 2 to'g'ri chiziqlar va x → + ∞ uchun y = p 2 (rasmdagi asimptotlar yashil chiziqlar).

1. Ark kotangent funktsiyasi: y = a r c c t g (x)

Ta'rif 25

Ark kotangent funktsiyasi xususiyatlari:

• ta'rif sohasi: x ∈ - ∞ ; +∞ ;
• diapazon: y ∈ (0 ; p) ;
• bu funksiya umumiy turdagi;
• funksiya butun ta'rif sohasi bo'yicha kamayib bormoqda;
• yoy kotangenti funksiyasi x ∈ [ 0 uchun botiq; + ∞) va x ∈ (- ∞ ; 0 ] uchun qavariqlik;
• burilish nuqtasi 0 koordinatalariga ega; p2;
• gorizontal asimptotlar x → - ∞ (chizmadagi yashil chiziq) da y = p to'g'ri chiziqlar va x → + ∞ da y = 0.

Agar siz matnda xatolikni sezsangiz, uni belgilab, Ctrl+Enter tugmalarini bosing

Quvvat funktsiyasi. Bu funksiya: y = ax n, qayerda a, n- doimiy. Da n= 1 olamiz to'g'ridan-to'g'ri proportsionallik: y = bolta; da n = 2 - kvadrat parabola ; da n = - 1 - teskari proportsionallik yoki giperbola. Shunday qilib, bu funktsiyalar kuch funktsiyasining maxsus holatlaridir. Biz bilamizki, har qanday nolga teng bo'lmagan raqamning nol darajasi 1, shuning uchun, da n= 0 quvvat funktsiyasi doimiy bo'ladi:y = a, ya'ni e. uning jadvali to'g'ri chiziq, o'q parallel X, kelib chiqishi bundan mustasno (aniqlik kiriting, nega? ). Bu holatlarning barchasi (bilan a= 1 ) 13-rasmda ko'rsatilgan (n 0 ) va 14-rasm ( n < 0). Отрицательные значения xbu erda hisobga olinmaydi ba'zi funktsiyalar kabi:

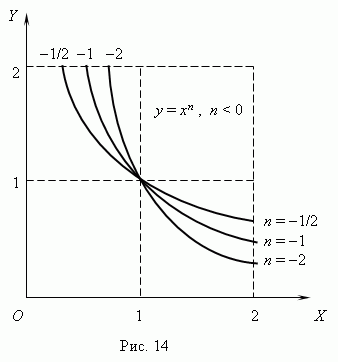
Agar a n– butun, quvvat funksiyalari qachon ham mantiqiyx< 0, но их графики имеют различный вид в зависимости от того, является ли njuft son yoki toq son. 15-rasmda ikkita quvvat funktsiyasi ko'rsatilgan: uchun n= 2 va n = 3.


Da n= 2 funksiya juft vauning grafigi simmetrikdir eksa haqida Y. Da n= 3 funksiya toq va uning grafigi koordinataga nisbatan simmetrik koordinatalar. Funktsiyay = x 3 chaqirdi kubik parabola.

16-rasmda funksiya ko'rsatilgan. Bu funksiya hisoblanadi kvadrat parabolaga teskari y = x 2 , uning grafigi grafikni aylantirish orqali olinadi kvadrat parabola 1-koordinata burchagi bissektrisasi atrofida. Bu har qanday grafikni olishning bir usuli teskari funktsiya uning asl funksiyasining grafigidan. Grafikdan bu ikki qiymatli funktsiya ekanligini ko'rishimiz mumkin (bu ± ning oldidagi ± belgisi bilan ham ko'rsatilgan. kvadrat ildiz). Bunday funktsiyalar elementar matematikada o'rganilmaydi, shuning uchun funktsiya sifatida biz odatda uning tarmoqlaridan birini ko'rib chiqamiz: yuqori yoki pastki.

Birinchidan, funksiya doirasini topishga harakat qiling:

Siz boshqardingizmi? Keling, javoblarni taqqoslaylik:

Hammasi to'g'ri? Barakalla!

Endi funksiya diapazonini topishga harakat qilaylik:

Topildimi? Taqqoslash:

Bu rozi bo'ldimi? Barakalla!

Keling, yana grafiklar bilan ishlaymiz, faqat hozir biroz qiyinroq - funksiya sohasini ham, funksiya diapazonini ham topish.

Funktsiyaning ham domenini, ham diapazonini qanday topish mumkin (Kengaytirilgan)

Mana nima bo'ldi:

Grafika bilan siz buni tushundingiz deb o'ylayman. Endi formulalarga muvofiq funktsiyaning sohasini topishga harakat qilaylik (agar buni qanday qilishni bilmasangiz, bu haqda bo'limni o'qing):

Siz boshqardingizmi? Tekshirish javoblar:

1. , chunki ildiz ifodasi noldan katta yoki teng bo'lishi kerak.
2. , chunki uni nolga bo'lish mumkin emas va radikal ifoda salbiy bo'lishi mumkin emas.
3. , beri, mos ravishda, hamma uchun.
4. chunki siz nolga bo'la olmaysiz.

Biroq, bizda hali hal qilinmagan yana bir lahza bor ...

Keling, ta'rifni takrorlab, unga e'tibor qarataman:

E'tibor berganmisiz? "Faqat" so'zi bizning ta'rifimizning juda muhim elementidir. Men sizga barmoqlar ustida tushuntirishga harakat qilaman.

Aytaylik, bizda to‘g‘ri chiziq bilan berilgan funksiya bor. . Qachon, biz bu qiymatni "qoida" ga almashtiramiz va buni olamiz. Bitta qiymat bitta qiymatga mos keladi. Buni tekshirish uchun biz hatto turli xil qiymatlar jadvalini tuzishimiz va berilgan funktsiyani tuzishimiz mumkin.

“Qarang! - deysiz, - "" ikki marta uchrashadi!" Demak, parabola funksiya emasdir? Yo'q, shunday!

"" ning ikki marta sodir bo'lishi parabolani noaniqlikda ayblash uchun asos emas!

Gap shundaki, hisob-kitob qilganimizda bizda bitta o'yin bor edi. Va hisob-kitob qilganda, bizda bitta o'yin bor. To'g'ri, parabola funksiyadir. Jadvalga qarang:

Tushundim? Agar yo'q bo'lsa, mana siz uchun matematikadan yiroq hayotiy misol!

Aytaylik, bizda bir guruh abituriyentlar hujjat topshirayotganda uchrashishdi, ularning har biri suhbatda qayerda yashashini aytdi:

Qabul qilaman, bir shaharda bir nechta yigitlar yashashi juda real, ammo bir kishi bir vaqtning o'zida bir nechta shaharda yashashi mumkin emas. Bu, go'yo bizning "parabola" ning mantiqiy timsoli - Bir xil y ga bir necha xil x mos keladi.

Keling, bog'liqlik funktsiya emasligiga misol keltiraylik. Aytaylik, o'sha yigitlar qaysi mutaxassisliklarga hujjat topshirganliklarini aytishdi:

Bu erda bizda butunlay boshqacha vaziyat mavjud: bir kishi bir yoki bir nechta yo'nalishlarga osongina murojaat qilishi mumkin. Ya'ni bitta element to'plamlar yozishmalarga qo'yiladi bir nechta elementlar to'plamlar. Mos ravishda, bu funksiya emas.

Keling, bilimingizni amalda sinab ko'raylik.

Rasmlardan funksiya nima ekanligini va nima emasligini aniqlang:

Tushundim? Va mana javoblar:

• Funktsiya - B, E.
• Funktsiya emas - A, B, D, D.

Nega deb so'rayapsizmi? Ha, nima uchun:

Bundan tashqari barcha raqamlarda DA) va E) bittasi uchun bir nechtasi bor!

Ishonchim komilki, endi siz funktsiyani nofunksiyadan bemalol ajrata olasiz, argument nima ekanligini va bog'liq o'zgaruvchi nima ekanligini ayta olasiz, shuningdek, argument doirasi va funksiya doirasini aniqlay olasiz. Keling, keyingi bo'limga o'tamiz - funktsiyani qanday aniqlash mumkin?

Funktsiyani o'rnatish usullari

Sizningcha, bu so'zlar nimani anglatadi "funktsiyani o'rnatish"? To'g'ri, bu holda biz qanday funktsiya haqida gapirayotganimizni hammaga tushuntirishni anglatadi. Bundan tashqari, hamma sizni to'g'ri tushunadigan tarzda tushuntiring va sizning tushuntirishingizga ko'ra odamlar tomonidan chizilgan funktsiyalarning grafiklari bir xil edi.

Buni qanday qilishim mumkin? Funktsiyani qanday o'rnatish kerak? Ushbu maqolada bir necha marta ishlatilgan eng oson usul - formuladan foydalanish. Biz formula yozamiz va unga qiymat qo'yish orqali biz qiymatni hisoblaymiz. Esingizda bo'lsa, formula bu qonun, qoida bo'lib, unga ko'ra X qanday Y ga aylanishi bizga va boshqa odamga ayon bo'ladi.

Odatda, ular aynan shunday qilishadi - vazifalarda biz formulalar bilan aniqlangan tayyor funktsiyalarni ko'ramiz, ammo har bir kishi unutadigan funktsiyani o'rnatishning boshqa usullari mavjud va shuning uchun "funktsiyani yana qanday qilib o'rnatishingiz mumkin?" Degan savol tug'iladi. chalg'itadi. Keling, hamma narsani tartibda ko'rib chiqaylik va analitik usuldan boshlaylik.

Funksiyani aniqlashning analitik usuli

Analitik usul - formuladan foydalangan holda funktsiyaning vazifasi. Bu eng universal va keng qamrovli va aniq yo'ldir. Agar sizda formula bo'lsa, unda siz funktsiya haqida mutlaqo hamma narsani bilasiz - siz uning bo'yicha qiymatlar jadvalini tuzishingiz, grafik yaratishingiz, funktsiya qayerda ko'payishi va qayerda kamayishini aniqlashingiz mumkin, umuman olganda, uni o'rganing. to `liq.

Funktsiyani ko'rib chiqaylik. Buning nima ahamiyati bor?

"Bu nima degani?" - deb so'raysiz. Men hozir tushuntiraman.

Eslatib o'taman, yozuvda qavs ichidagi ifoda argument deb ataladi. Va bu dalil har qanday ifoda bo'lishi mumkin, oddiy bo'lishi shart emas. Shunga ko'ra, qanday argument bo'lishidan qat'i nazar (qavs ichidagi ifoda), biz uni ifoda o'rniga yozamiz.

Bizning misolimizda u quyidagicha ko'rinadi:

Imtihonda bo'ladigan funktsiyani belgilashning analitik usuli bilan bog'liq boshqa vazifani ko'rib chiqing.

ifoda qiymatini toping, da.

Ishonchim komilki, siz avvaliga bunday iborani ko'rganingizda qo'rqdingiz, lekin unda hech qanday qo'rqinchli narsa yo'q!

Hammasi oldingi misoldagidek: argument nima bo'lishidan qat'i nazar (qavs ichidagi ifoda), biz uni ifoda o'rniga yozamiz. Masalan, funktsiya uchun.

Bizning misolimizda nima qilish kerak? Buning o'rniga siz yozishingiz kerak va o'rniga -:

olingan ifodani qisqartiring:

Hammasi shu!

Mustaqil ish

Endi quyidagi iboralarning ma'nosini o'zingiz topishga harakat qiling:

1. , agar
2. , agar

Siz boshqardingizmi? Keling, javoblarimizni taqqoslaylik: Biz funktsiyaning shaklga ega ekanligiga o'rganib qolganmiz

Hatto misollarimizda ham biz funktsiyani shu tarzda aniqlaymiz, lekin analitik jihatdan, masalan, funktsiyani aniq belgilash mumkin.

Ushbu funktsiyani o'zingiz yaratishga harakat qiling.

Siz boshqardingizmi?

Mana, men uni qanday qurdim.

Biz qanday tenglamaga erishdik?

To'g'ri! Chiziqli, ya'ni grafik to'g'ri chiziq bo'ladi. Bizning chiziqqa qaysi nuqtalar tegishli ekanligini aniqlash uchun jadval tuzamiz:

Bu biz gaplashayotgan narsa edi ... Biri bir nechtasiga to'g'ri keladi.

Keling, nima bo'lganini chizishga harakat qilaylik:

Bizda bor narsa funksiya bormi?

To'g'ri, yo'q! Nega? Bu savolga rasm bilan javob berishga harakat qiling. Nima oldingiz?

"Chunki bitta qiymat bir nechta qiymatlarga mos keladi!"

Bundan qanday xulosa chiqarishimiz mumkin?

To'g'ri, funktsiyani har doim ham aniq ifodalash mumkin emas va funktsiya sifatida "niqoblangan" narsa har doim ham funktsiya bo'lavermaydi!

Funksiyani aniqlashning jadval usuli

Nomidan ko'rinib turibdiki, bu usul oddiy plastinka. Ha ha. Biz allaqachon qilganimiz kabi. Misol uchun:

Bu erda siz darhol naqshni payqadingiz - Y X dan uch baravar katta. Va endi "yaxshi o'ylang" vazifasi: jadval ko'rinishida berilgan funktsiya funktsiyaga ekvivalent deb o'ylaysizmi?

Keling, uzoq vaqt gaplashmaylik, lekin chizamiz!

Shunday qilib. Biz ikkala usulda berilgan funktsiyani chizamiz:

Farqni ko'ryapsizmi? Bu belgilangan nuqtalar haqida emas! Yaqindan ko'rib chiqing:

Endi ko'rdingizmi? Funktsiyani jadval shaklida o'rnatganimizda, biz grafikda faqat jadvalda mavjud bo'lgan nuqtalarni aks ettiramiz va chiziq (bizning holatimizda bo'lgani kabi) faqat ular orqali o'tadi. Funksiyani analitik usulda aniqlaganimizda, istalgan nuqtani olishimiz mumkin va bizning funksiyamiz ular bilan cheklanmaydi. Mana shunday xususiyat. Eslab qoling!

Funksiyani yaratishning grafik usuli

Grafik usul funktsiyani qurish qulayroq emas. Biz o'z funktsiyamizni chizamiz va boshqa qiziqqan kishi ma'lum bir x da y ga teng ekanligini topishi mumkin va hokazo. Grafik va analitik usullar eng keng tarqalgan.

Biroq, bu erda siz boshida nima haqida gaplashganimizni eslab qolishingiz kerak - koordinatalar tizimida chizilgan har bir "chiziq" funktsiya emas! Esingizdami? Har holda, funksiya nima ekanligini bu yerga ko'chirib olaman:

Qoidaga ko'ra, odamlar odatda biz tahlil qilgan funksiyani ko'rsatishning aynan shu uchta usulini nomlashadi - analitik (formuladan foydalangan holda), jadval va grafik, funktsiyani og'zaki tasvirlash mumkinligini butunlay unutib qo'yishadi. Bu qanday? Ha, juda oson!

Funktsiyaning og'zaki tavsifi

Funktsiyani og'zaki qanday tasvirlash mumkin? Keling, so'nggi misolimizni olaylik - . Bu funksiya"x ning har bir haqiqiy qiymati uning uchlik qiymatiga mos keladi" deb ta'riflash mumkin. Hammasi shu. Hech narsa murakkab emas. Albatta, siz e'tiroz bildirasiz - "shunday murakkab funktsiyalar mavjudki, ularni og'zaki ravishda belgilashning iloji yo'q!" Ha, ba'zilari bor, lekin formulalar bilan belgilashdan ko'ra og'zaki tasvirlash osonroq bo'lgan funktsiyalar mavjud. Masalan: "x ning har bir natural qiymati u tashkil etgan raqamlar orasidagi farqga to'g'ri keladi, son yozuvidagi eng katta raqam esa minuend sifatida qabul qilinadi." Endi funktsiyaning og'zaki tavsifi amalda qanday amalga oshirilishini ko'rib chiqing:

Berilgan sondagi eng katta raqam - mos ravishda - qisqartiriladi, keyin:

Funksiyalarning asosiy turlari

Endi eng qiziqarlisiga o'tamiz - biz siz ishlagan / ishlagan va maktab va institut matematikasi kurslarida ishlagan funktsiyalarning asosiy turlarini ko'rib chiqamiz, ya'ni biz ular bilan tanishamiz va ularga bering qisqacha tavsif. Har bir funktsiya haqida ko'proq ma'lumotni tegishli bo'limda o'qing.

Chiziqli funksiya

Shaklning funktsiyasi, bu erda haqiqiy sonlar.

Ushbu funktsiyaning grafigi to'g'ri chiziq, shuning uchun qurilish chiziqli funksiya ikki nuqtaning koordinatalarini topishga qisqartiriladi.

To'g'ridan-to'g'ri pozitsiya yoqilgan koordinata tekisligi qiyalik omiliga bog'liq.

Funktsiya doirasi (aka argument diapazoni) - .

Qiymatlar diapazoni .

kvadratik funktsiya

Shaklning vazifasi, bu erda

Funktsiya grafigi parabola bo'lib, parabola shoxlari pastga yo'naltirilganda, yuqoriga.

Ko'p mulk kvadratik funktsiya diskriminantning qiymatiga bog'liq. Diskriminant formula bo'yicha hisoblanadi

Parabolaning qiymat va koeffitsientga nisbatan koordinata tekisligidagi holati rasmda ko'rsatilgan:

Domen

Qiymatlar diapazoni berilgan funktsiyaning ekstremumiga (parabolaning cho'qqisiga) va koeffitsientga (parabola shoxlarining yo'nalishi) bog'liq.

Teskari proportsionallik

Formula bilan berilgan funktsiya, bu erda

Raqam teskari proportsionallik omili deb ataladi. Qaysi qiymatga qarab, giperbolaning shoxlari turli kvadratlarda joylashgan:

Domen - .

Qiymatlar diapazoni .

XULOSA VA ASOSIY FORMULA

1. Funksiya - bu qoida bo'lib, unga ko'ra to'plamning har bir elementiga to'plamning yagona elementi beriladi.

• - bu funktsiyani, ya'ni bir o'zgaruvchining boshqasiga bog'liqligini bildiruvchi formula;
• - o'zgaruvchi yoki argument;
• - qaram qiymat - argument o'zgarganda o'zgaradi, ya'ni ba'zilarga ko'ra ma'lum formula, bir miqdorning boshqasiga bog'liqligini aks ettiradi.

2. Yaroqli argument qiymatlari, yoki funktsiya doirasi - bu funktsiya mantiqiy bo'lgan mumkin bo'lgan narsa bilan bog'liq.

3. Funksiya qiymatlari diapazoni- bu haqiqiy qiymatlarga ega bo'lgan qiymatlarni oladi.

4. Funktsiyani o'rnatishning 4 ta usuli mavjud:

• analitik (formulalar yordamida);
• jadvalli;
• grafik
• og'zaki tavsif.

5. Funksiyalarning asosiy turlari:

• : , bu yerda, haqiqiy sonlar;
• : , qaerda;
• : , qayerda.

Milliy tadqiqot universiteti

Amaliy geologiya kafedrasi

Mavhum oliy matematika

Mavzu bo'yicha: "Asosiy elementar funktsiyalar,

ularning xossalari va grafiklari"

Bajarildi:

Tekshirildi:

o'qituvchi

Ta'rif. y=a x formula bilan berilgan funksiya (bu yerda a>0, a≠1) asosi a bo‘lgan ko‘rsatkichli funksiya deyiladi.

Eksponensial funktsiyaning asosiy xossalarini tuzamiz:

1. Ta'rif sohasi - barcha haqiqiy sonlar to'plami (R).

2. Qiymatlar diapazoni barcha musbat haqiqiy sonlar to‘plami (R+) hisoblanadi.

3. a > 1 bo'lganda, funktsiya butun real chiziqda ortadi; 0 da<а<1 функция убывает.

4. Umumiy funksiya hisoblanadi.

, xO [-3;3] oraliqda, xO [-3;3] oraliqda

y(x)=x n ko‘rinishdagi funksiya, bunda n OR soni bo‘lib, daraja funksiyasi deyiladi. n soni turli qiymatlarni qabul qilishi mumkin: ham butun, ham kasr, ham juft, ham toq. Bunga qarab, quvvat funktsiyasi boshqa shaklga ega bo'ladi. Quvvat funktsiyalari bo'lgan va ushbu turdagi egri chiziqlarning asosiy xususiyatlarini quyidagi tartibda aks ettiruvchi maxsus holatlarni ko'rib chiqing: quvvat funktsiyasi y \u003d x² (juft ko'rsatkichli funktsiya - parabola), quvvat funktsiyasi y \u003d x³ (funksiya). g'alati ko'rsatkichli - kub parabola) va y \u003d √ x funktsiyasi (x ½ kuchiga) (kasr ko'rsatkichli funktsiya), manfiy butun ko'rsatkichli funktsiya (giperbola).

Quvvat funktsiyasi y=x²

1. D(x)=R – funksiya butun son o‘qda aniqlanadi;

2. E(y)= va oraliqda ortadi

Quvvat funktsiyasi y=x³

1. y \u003d x³ funksiyaning grafigi kubik parabola deb ataladi. y=x³ quvvat funksiyasi quyidagi xususiyatlarga ega:

2. D(x)=R – funksiya butun son o‘qda aniqlanadi;

3. E(y)=(-∞;∞) – funksiya oʻzining taʼrif sohasidagi barcha qiymatlarni oladi;

4. x=0 y=0 bo’lganda – funksiya O(0;0) koordinatadan o’tadi.

5. Funktsiya butun ta'rif sohasi bo'ylab ortadi.

6. Funksiya gʻalati (koordinata boshiga nisbatan simmetrik).

, xn [-3;3] oraliqda

X³ oldidagi raqamli omilga qarab, funktsiya tik / tekis va oshirish / kamaytirish bo'lishi mumkin.

Butun manfiy darajali quvvat funksiyasi:

Agar n ko'rsatkichi toq bo'lsa, unda bunday daraja funksiyasining grafigi giperbola deb ataladi. Manfiy butun ko‘rsatkichli quvvat funksiyasi quyidagi xususiyatlarga ega:

1. Har qanday n ta uchun D(x)=(-∞;0)U(0;∞);

2. E(y)=(-∞;0)U(0;∞) agar n toq son bo’lsa; E(y)=(0;∞) agar n juft son bo'lsa;

3. Agar n toq son bo'lsa, funksiya butun ta'rif sohasi bo'ylab kamayadi; funktsiya (-∞;0) intervalda ortadi va (0;∞) oraliqda kamayadi, agar n juft son bo'lsa.

4. Agar n toq son bo lsa, funksiya toq (koordinata boshiga nisbatan simmetrik); funktsiya n juft son bo'lsa ham.

5. Funksiya agar n toq son bo‘lsa (1;1) va (-1;-1) nuqtalardan, agar n juft son bo‘lsa (1;1) va (-1;1) nuqtalardan o‘tadi.

, xn [-3;3] oraliqda

Kasr ko'rsatkichli quvvat funksiyasi

Shaklning (rasm) kasr ko'rsatkichiga ega bo'lgan quvvat funktsiyasi rasmda ko'rsatilgan funktsiyaning grafigiga ega. Kasr darajali daraja funksiyasi quyidagi xususiyatlarga ega: (rasm)

1. D(x) OR, agar n toq son bo‘lsa va D(x)= bo‘lsa, xO oralig‘ida, xO [-3;3] oralig‘ida.

y \u003d log a x logarifmik funksiyasi quyidagi xususiyatlarga ega:

1. Aniqlanish sohasi D(x)n (0; + ∞).

2. E(y) qiymatlar diapazoni O (- ∞; + ∞)

3. Funksiya juft ham, toq ham emas (umumiy).

4. Funksiya a > 1 uchun (0; + ∞) oraliqda ortadi, 0 uchun (0; + ∞) kamayadi.< а < 1.

y = log a x funksiya grafigini y = a x funksiya grafigidan y = x chiziqqa nisbatan simmetriya o zgartirishdan foydalanib olish mumkin. 9-rasmda a > 1 uchun logarifmik funksiya grafigi, 10-rasmda esa 0 uchun chizilgan.< a < 1.

; xn oralig'ida; xO oralig'ida

y \u003d sin x, y \u003d cos x, y \u003d tg x, y \u003d ctg x funktsiyalari deyiladi. trigonometrik funktsiyalar.

y \u003d sin x, y \u003d tg x, y \u003d ctg x funktsiyalari toq, y \u003d cos x funksiyasi esa juft.

Funktsiya y \u003d sin (x).

1. Ta'rif sohasi D(x) OR.

2. E(y) qiymatlar diapazoni O [ - 1; biri].

3. Funksiya davriy; asosiy davr 2p.

4. Funktsiya toq.

5. Funksiya [ -p/2 + 2pn oraliqlarida ortadi; p/2 + 2pn] va [ p/2 + 2pn] oraliqlarida kamayadi; 3p/2 + 2pn], n O Z.

y \u003d sin (x) funktsiyasining grafigi 11-rasmda ko'rsatilgan.