mavzu :

Maqsad : Teskari hosilalarning hosilalari haqida tushuncha hosil qilish trigonometrik funktsiyalar.

Vazifalar:

1. bu funktsiyalarning hosilalarini topishni o'rganing;yordamida talabalar bilan ushbu funktsiyalarni farqlash qobiliyatini ishlab chiqish
mustaqil ish va o'zaro tekshirish;

2. matematika, hisoblash va fanlarga qiziqishni rivojlantirish kognitiv ko'nikmalar,
boshqa talabalarning xatolarini tahlil qilish qobiliyati;

3. ongni, mustaqillikni tarbiyalash

1. Tashkiliy moment
Talabalar bilan salomlashaman, darsda ishlash qoidalari bilan tanishtiraman, reyting varaqasini to‘g‘ri to‘ldirishni tushuntiraman.
2.Motivatsion bosqich
Talabalar mavzu bo'yicha bilishlari va qila olishlari kerak bo'lgan narsalarni o'qiydilar.
Boshlashdan oldin, ESLASH qoidasini o'qing.
3. Operatsion bosqich
Talabalar ish varag'ini to'ldiradilar (ilova qilingan)
4.Darsning qisqacha mazmuni
Reflektsiya.

Bugun darsda:

Men o'rgandim…

Bu qiziq edi…

Bu qiyin edi…

Men muvaffaq bo'ldim…

Men sinab ko'raman…

O'QUV VRAFI

ushbu mavzu bo'yicha: Trigonometrik va teskari trigonometrik funksiyalarning hosilalari.

2 ta dars.

MAVZUNI O'RGANISH NATIJASIDA KERAK.

BILING: uchun farqlash formulalari trigonometrik va teskari trigonometrik funktsiyalar.

IMKONIYATIGA EGA BO'LISH: trigonometrik va teskari trigonometrik funksiyalarning hosilalarini toping.

eslab qoling , algoritm ishlashi kerak.

Testdan o'tishni, chetiga eslatmalarni qo'yishni, mavzuning reyting varaqasini to'ldirishni unutmang.

Iltimos, javobsiz qolgan savollaringizni qoldirmang.

Tekshiruv davomida ob'ektiv bo'ling, bu sizga ham, siz tekshirayotgan odamga ham yordam beradi.

SIZGA MUVAFFAQIYAT TILAYMIZ!

Z ADANIE №1

Teskari trigonometrik funksiyalarni farqlash formulalarini o‘qing va o‘rganing: (2 p.)

Agar funktsiya murakkab bo'lsa, u holda

qayerda z - elementar funktsiya

Misollarni ko'rib chiqing:

y=arcsin(x) keyin y/=

y = arcctg(3x 2 -4) bo'lsa

y/=

hosilalarni toping:(3 p.)

y= arcsin(-x) y= arctg(-x) y= arcos(2x)

P TEKSHIRING №1

Z ADANIE №2

Misollardan birini yeching: (3b)

lekin ) y = arkos (5x - 3)

b ) y = arcctg(7x+1)

P TEKSHIRING №2

Z ADANIE №3

a) Misolning yechimini yana bir bor ko'rib chiqing:

b) funksiyalarning hosilalarini toping (4 b.)

arcsin (2x 2 - 5x)

arccos (4x 2 - 6x)

P TEKSHIRING №3

Z ADANIE №4

Barakalla! Siz boshlashingiz mumkintekshirish ishi raqami 1.

№5 topshiriq

a) Misolning yechimini ko'rib chiqing:

b) funksiyalarning hosilalarini toping (6 b.)

P TEKSHIRING №5

Barakalla! Siz boshlashingiz mumkintekshirish ishi raqami 2.

Tekshirish ishi №1

Variantlardan birini bajaring (11b)

1v 2v

1. Hosilalarni toping quyidagi funktsiyalar:

a) 2 ball

y = arctg(-2x) y = arccos(3x)

b) 4 ball

y = arkos (3x 2 - 2) y = arcctg(2x 3 +1)

c) 5 ball

y = arksin (x 2 - 5x) + tan (2x+1) y = arkkos(3x 2 - 2x) + ctg(x+4) maks

ball

qabul qildi

Hisob

JSSV

tekshirildi

daraja

2 b

3 b

1 1 b

6 b

1 4 b

jami

43 b

JAMI 43 ball

"5" - 33 - 43 ball;

"4" - 24 - 32 ball;

"3" - 18 - 23 ball.

Mavzuni o'rganishda qulaylik va ravshanlik uchun bu erda yig'ma jadval mavjud.

Doimiyy=C

Quvvat funktsiyasi y = x p

(x p)" = p x p - 1

Eksponensial funktsiyay = x

(a x)" = a x ln a

Xususan, qachona = ebizda ... bor y = e x

(e x)" = e x

logarifmik funktsiya

(log a x) " = 1 x ln a

Xususan, qachona = ebizda ... bor y = log x

(ln x)" = 1 x

Trigonometrik funktsiyalar

(sin x) "= cos x (cos x)" = - sin x (t g x) " = 1 cos 2 x (c t g x)" = - 1 sin 2 x

Teskari trigonometrik funksiyalar

(a r c sin x) " = 1 1 - x 2 (a r c cos x) " = - 1 1 - x 2 (a r c t g x) " = 1 1 + x 2 (a r c c t g x) " = - 1 1 + x 2

Giperbolik funktsiyalar

(s h x) " = c h x (c h x) " = s h x (t h x) " = 1 c h 2 x (c t h x) " = - 1 s h 2 x

Keling, ko'rsatilgan jadval formulalari qanday olinganligini tahlil qilaylik yoki boshqacha qilib aytganda, har bir funktsiya turi uchun hosilalar uchun formulalar hosil bo'lishini isbotlaymiz.

Doimiy miqdorning hosilasi

Isbot 1

Bu formulani chiqarish uchun funktsiyaning nuqtadagi hosilasi ta'rifini asos qilib olamiz. Biz x 0 = x dan foydalanamiz, bu erda x har qanday haqiqiy sonning qiymatini oladi, yoki boshqacha qilib aytganda, x f (x) = C funktsiya sohasining istalgan soni. Funksiya ortishining argument ortishiga nisbati chegarasini ∆ x → 0 shaklida yozamiz:

lim ∆ x → 0 ∆ f (x) ∆ x = lim ∆ x → 0 C - C ∆ x = lim ∆ x → 0 0 ∆ x = 0

E'tibor bering, 0 ∆ x ifodasi chegara belgisi ostiga tushadi. Bu "nolning nolga bo'linishi" ning noaniqligi emas, chunki numerator cheksiz emas. kichik qiymat, ya'ni nol. Boshqacha qilib aytganda, doimiy funktsiyaning o'sishi har doim nolga teng.

Demak, f (x) = C doimiy funksiyasining hosilasi butun taʼrif sohasi boʻyicha nolga teng.

1-misol

Berilgan doimiy funktsiyalar:

f 1 (x) = 3 , f 2 (x) = a , a ∈ R , f 3 (x) = 4 . 13 7 22 , f 4 (x) = 0 , f 5 (x) = - 8 7

Yechim

Keling, berilgan shartlarni tavsiflaymiz. Birinchi funksiyada 3 natural sonining hosilasini ko'ramiz. Quyidagi misolda siz ning hosilasini olishingiz kerak lekin, qayerda lekin- har qanday haqiqiy raqam. Uchinchi misol bizga hosilani beradi irratsional son 4 . 13 7 22, to'rtinchisi - nolning hosilasi (nol butun son). Nihoyat, beshinchi holatda biz ratsional kasrning hosilasiga egamiz - 8 7 .

Javob: hosilalari funktsiyalarni o'rnatish har qanday real uchun nolga teng x(butun ta'rif sohasi bo'yicha)

f 1 " (x) = (3) " = 0 , f 2 " (x) = (a) " = 0 , a ∈ R , f 3 " (x) = 4 . 13 7 22 " = 0 , f 4 " (x) = 0 " = 0 , f 5 " (x) = - 8 7 " = 0

Quvvat funksiyasi hosilasi

Keling, davom etaylik quvvat funktsiyasi va uning hosilasi formulasi, bu shaklga ega: (x p) " = p x p - 1, bu erda ko'rsatkich p har qanday haqiqiy sondir.

Isbot 2

Ko'rsatkich bo'lganda formulaning isbotini keltiramiz natural son: p = 1, 2, 3, …

Shunga qaramay, biz hosila ta'rifiga tayanamiz. Quvvat funksiyasi ortishining argument ortishiga nisbati chegarasini yozamiz:

(x p) " = lim ∆ x → 0 = ∆ (x p) ∆ x = lim ∆ x → 0 (x + ∆ x) p - x p ∆ x

Numeratordagi ifodani soddalashtirish uchun Nyutonning binomial formulasidan foydalanamiz:

(x + ∆ x) p - x p = C p 0 + x p + C p 1 x p - 1 ∆ x + C p 2 x p - 2 (∆ x) 2 + . . . + + C pp - 1 x (∆ x) p - 1 + C pp (∆ x) p - xp = = C p 1 xp - 1 ∆ x + C p 2 xp - 2 (∆ x) 2 +. . . + C p p - 1 x (∆ x) p - 1 + C p p (∆ x) p

Shunday qilib:

(xp) " = lim ∆ x → 0 ∆ (xp) ∆ x = lim ∆ x → 0 (x + ∆ x) p - xp ∆ x = = lim ∆ x → 0 (C p 1 xp - 1 ∆ x + C p 2 xp - 2 (∆ x) 2 + .. + C pp - 1 x (∆ x) p - 1 + C pp (∆ x) p) ∆ x = = lim ∆ x → 0 (C p 1) xp - 1 + C p 2 xp - 2 ∆ x + .. + C pp - 1 x (∆ x) p - 2 + C pp (∆ x) p - 1) = = C p 1 xp - 1 + 0 + 0 + ... + 0 = p! 1! (p - 1)! xp - 1 = p xp - 1

Demak, ko‘rsatkich natural son bo‘lganda daraja funksiyasining hosilasi formulasini isbotladik.

Isbot 3

Qachon ish uchun dalil berish p- noldan boshqa har qanday haqiqiy son, biz logarifmik hosiladan foydalanamiz (bu erda biz logarifmik funktsiyaning hosilasidan farqni tushunishimiz kerak). To'liqroq tushunish uchun logarifmik funktsiyaning hosilasini o'rganish va qo'shimcha ravishda aniq berilgan funktsiyaning hosilasi va hosilasini ko'rib chiqish maqsadga muvofiqdir. murakkab funktsiya.

Ikkita holatni ko'rib chiqing: qachon x ijobiy va qachon x salbiy.

Shunday qilib, x > 0. Keyin: x p > 0 . Biz y \u003d x p tengligining logarifmini e asosiga olamiz va logarifmning xususiyatini qo'llaymiz:

y = x p ln y = ln x p ln y = p ln x

Ushbu bosqichda aniq belgilangan funktsiya olindi. Keling, uning hosilasini aniqlaymiz:

(ln y) " = (p ln x) 1 y y " = p 1 x ⇒ y " = p y x = p x p x = p x p - 1

Endi biz qachon ishni ko'rib chiqamiz x- manfiy raqam.

Agar ko'rsatkich p juft son bo'lsa, u holda quvvat funksiyasi x uchun ham aniqlanadi< 0 , причем является четной: y (x) = - y ((- x) p) " = - p · (- x) p - 1 · (- x) " = = p · (- x) p - 1 = p · x p - 1

Keyin xp< 0 и возможно составить доказательство, используя логарифмическую производную.

Agar p toq son bo'lsa, u holda quvvat funksiyasi x uchun aniqlanadi< 0 , причем является нечетной: y (x) = - y (- x) = - (- x) p . Тогда x p < 0 , а значит логарифмическую производную задействовать нельзя. В такой ситуации возможно взять за основу доказательства правила дифференцирования и правило нахождения производной сложной функции:

y "(x) \u003d (- (- x) p) " \u003d - ((- x) p) " \u003d - p (- x) p - 1 (- x) " = \u003d p (- x ) p - 1 = p xp - 1

Oxirgi o'tish mumkin, chunki agar p demak, bu toq raqam p - 1 juft son yoki nol (p = 1 uchun), shuning uchun salbiy uchun x(- x) p - 1 = x p - 1 tengligi to'g'ri.

Shunday qilib, biz har qanday haqiqiy p uchun darajali funksiya hosilasi formulasini isbotladik.

2-misol

Berilgan funktsiyalar:

f 1 (x) = 1 x 2 3 , f 2 (x) = x 2 - 1 4 , f 3 (x) = 1 x log 7 12

Ularning hosilalarini aniqlang.

Yechim

Berilgan funksiyalarning bir qismini daraja xossalariga asoslanib jadval ko‘rinishiga y = x p ga aylantiramiz va keyin formuladan foydalanamiz:

f 1 (x) \u003d 1 x 2 3 \u003d x - 2 3 ⇒ f 1 "(x) \u003d - 2 3 x - 2 3 - 1 \u003d - 2 3 x - 5 3 f 2 "(x) \u003d x 2 - 1 4 = 2 - 1 4 x 2 - 1 4 - 1 = 2 - 1 4 x 2 - 5 4 f 3 (x) = 1 x log 7 12 = x - log 7 12 ⇒ f 3 " ( x) = - log 7 12 x - log 7 12 - 1 = - log 7 12 x - log 7 12 - log 7 7 = - log 7 12 x - log 7 84

Ko'rsatkichli funktsiyaning hosilasi

Isbot 4

Ta'rifga asoslanib, hosila uchun formulani olamiz:

(ax) " = lim ∆ x → 0 ax + ∆ x - ax ∆ x = lim ∆ x → 0 ax (a ∆ x - 1) ∆ x = ax lim ∆ x → 0 a ∆ x - 1 ∆ x = 0 0

Bizda noaniqlik paydo bo'ldi. Uni kengaytirish uchun z = a ∆ x - 1 yangi o'zgaruvchini yozamiz (z → 0 ni ∆ x → 0 sifatida). Bu holda a ∆ x = z + 1 ⇒ ∆ x = log a (z + 1) = ln (z + 1) ln a . Oxirgi o'tish uchun logarifmning yangi bazasiga o'tish formulasi qo'llaniladi.

Keling, asl chegarada almashtirishni amalga oshiramiz:

(ax) " = ax lim ∆ x → 0 a ∆ x - 1 ∆ x = ax ln a lim ∆ x → 0 1 1 z ln (z + 1) = ax ln a lim ∆ x → 0 1 ln (z +) 1) 1 z = ax ln a 1 ln lim ∆ x → 0 (z + 1) 1 z

Ikkinchi ajoyib chegarani eslang va keyin hosila uchun formulani olamiz eksponensial funktsiya:

(a x) " = a x ln a 1 ln lim z → 0 (z + 1) 1 z = a x ln a 1 ln e = a x ln a

3-misol

Eksponensial funktsiyalar berilgan:

f 1 (x) = 2 3 x , f 2 (x) = 5 3 x , f 3 (x) = 1 (e) x

Biz ularning hosilalarini topishimiz kerak.

Yechim

Eksponensial funktsiyaning hosilasi va logarifmning xususiyatlari uchun formuladan foydalanamiz:

f 1 "(x) = 2 3 x" = 2 3 x ln 2 3 = 2 3 x (ln 2 - ln 3) f 2 "(x) = 5 3 x" = 5 3 x ln 5 1 3 = 1 3 5 3 x ln 5 f 3 "(x) = 1 (e) x" = 1 ex "= 1 ex ln 1 e = 1 ex ln e - 1 = - 1 ex

Logarifmik funktsiyaning hosilasi

Isbot 5

Har qanday logarifmik funktsiyaning hosilasi formulasining isbotini keltiramiz x ta'rif sohasida va logarifmning a asosining har qanday haqiqiy qiymatlari. Loyimaning ta'rifiga asoslanib, biz quyidagilarni olamiz:

(log ax) " = lim ∆ x → 0 log a (x + ∆ x) - log ax ∆ x = lim ∆ x → 0 log ax + ∆ xx ∆ x = = lim ∆ x → 0 1 ∆ x log a 1 + ∆ xx = lim ∆ x → 0 log a 1 + ∆ xx 1 ∆ x = = lim ∆ x → 0 log a 1 + ∆ xx 1 ∆ x xx = lim ∆ x → 0 1 x log a 1 + ∆ xx x = = 1 x log a lim ∆ x → 0 1 + ∆ xxx ∆ x = 1 x log ae = 1 x ln e ln a = 1 x ln a

Belgilangan tenglik zanjiridan ko'rish mumkinki, o'zgartirishlar logarifm xossasi asosida qurilgan. lim ∆ x → 0 1 + ∆ x x x ∆ x = e tengligi ikkinchi ajoyib chegaraga muvofiq to'g'ri.

4-misol

Logarifmik funksiyalar berilgan:

f 1 (x) = log log 3 x , f 2 (x) = log x

Ularning hosilalarini hisoblash kerak.

Yechim

Olingan formulani qo'llaymiz:

f 1 "(x) = (log ln 3 x)" = 1 x ln (ln 3) ; f 2 "(x) \u003d (ln x)" \u003d 1 x ln e \u003d 1 x

Shunday qilib, natural logarifmning hosilasi bir ga bo'linadi x.

Trigonometrik funksiyalarning hosilalari

Isbot 6

Biz ba'zilarini ishlatamiz trigonometrik formulalar va trigonometrik funktsiyaning hosilasi formulasini olishning birinchi ajoyib chegarasi.

Sinus funktsiyasining hosilasi ta'rifiga ko'ra, biz quyidagilarni olamiz:

(sin x) " = lim ∆ x → 0 sin (x + ∆ x) - sin x ∆ x

Sinuslar farqi formulasi bizga quyidagi amallarni bajarishga imkon beradi:

(sin x) " = lim ∆ x → 0 sin (x + ∆ x) - sin x ∆ x = = lim ∆ x → 0 2 sin x + ∆ x - x 2 cos x + ∆ x + x 2 ∆ x = = lim ∆ x → 0 sin ∆ x 2 cos x + ∆ x 2 ∆ x 2 = = cos x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2

Va nihoyat, biz birinchi ajoyib chegaradan foydalanamiz:

sin "x = cos x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = cos x

Demak, funktsiyaning hosilasi gunoh x bo'ladi chunki x.

Kosinus hosilasi formulasini ham xuddi shunday isbotlaymiz:

cos "x = lim ∆ x → 0 cos (x + ∆ x) - cos x ∆ x = = lim ∆ x → 0 - 2 sin x + ∆ x - x 2 sin x + ∆ x + x 2 ∆ x = = - lim ∆ x → 0 sin ∆ x 2 sin x + ∆ x 2 ∆ x 2 = = - sin x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = - sin x

Bular. cos x funksiyaning hosilasi bo'ladi - sin x.

Differensiallash qoidalariga asoslanib tangens va kotangens hosilalari uchun formulalarni olamiz:

tg "x = sin x cos x" = sin "x cos x - sin x cos" x cos 2 x = = cos x cos x - sin x (- sin x) cos 2 x = sin 2 x + cos 2 x cos 2 x = 1 cos 2 xctg "x = cos x sin x" = cos "x sin x - cos x sin" x sin 2 x = = - sin x sin x - cos x cos x sin 2 x = - sin 2 x + cos 2 x sin 2 x = - 1 sin 2 x

Teskari trigonometrik funksiyalarning hosilalari

Hosil bo'limi teskari funktsiyalar arksinus, arkkosinus, arktangens va arkkotangens hosilalarining formulalarini isbotlash haqida keng qamrovli ma'lumot beradi, shuning uchun biz bu erda materialni takrorlamaymiz.

Giperbolik funksiyalarning hosilalari

Isbot 7

Giperbolik sinus, kosinus, tangens va kotangens hosilalari uchun differensiallash qoidasi va eksponensial funktsiya hosilasi formulasidan foydalanib formulalarni olishimiz mumkin:

sh "x = ex - e - x 2" = 1 2 ex " - e - x " == 1 2 ex - - e - x = ex + e - x 2 = chxch " x = ex + e - x 2 " = 1 2 ex "+e - x" == 1 2 ex + - e - x = ex - e - x 2 = shxth "x = shxchx" = sh "x chx - shx ch" xch 2 x = ch 2 x - sh 2 xch 2 x = 1 ch 2 xcth "x = chxshx" = ch "x shx - chx sh" xsh 2 x = sh 2 x - ch 2 xsh 2 x = - 1 sh 2 x

Agar siz matnda xatolikni sezsangiz, uni belgilab, Ctrl+Enter tugmalarini bosing

Topish uchun trigonometrik funktsiyaning hosilasi foydalanish kerak hosilaviy jadval, ya'ni 6-13 hosilalari.

Qachon topilgan oddiy trigonometrik funksiyalarning hosilalari Umumiy xatolarga yo'l qo'ymaslik uchun quyidagi fikrlarga e'tibor bering.

funktsiya ifodasida atamalardan biri tez-tez bo'ladi sinus, kosinus yoki boshqa trigonometrik funktsiya funktsiya argumentidan emas, balki sondan (doimiy), shuning uchun bu atamaning hosilasi nolga teng;
deyarli har doim siz differentsiatsiya natijasida olingan ifodani soddalashtirishingiz kerak va buning uchun siz kasrlar bilan operatsiyalar bo'yicha bilimlardan ishonchli foydalanishingiz kerak;
ifodani soddalashtirish uchun deyarli har doim trigonometrik identifikatsiyalarni bilish kerak, masalan, qo'sh burchak formulasi va sinus va kosinus kvadratlarining yig'indisi sifatida birlik formulasi.

1-misol Funktsiyaning hosilasini toping

Yechim. bilan aytaylik kosinus hosilasi hamma narsa aniq, lotinlarni o'rganishni boshlagan ko'pchilik aytadi. Bilan-chi sinus hosilasi o'n ikki pi ga bo'linadi? Javob: nolga teng deb hisoblang! Bu erda sinus (axir funktsiya!) tuzoqdir, chunki argument x o'zgaruvchisi yoki boshqa o'zgaruvchi emas, shunchaki raqamdir. Ya'ni, bu sonning sinusi ham sondir. Va sonning hosilasi (doimiy), biz hosilalar jadvalidan bilganimizdek, nolga teng. Shunday qilib, biz x ning faqat minus sinusini qoldiramiz va uning hosilasini topamiz, belgini unutmaymiz:

2-misol Funktsiyaning hosilasini toping

Yechim. Ikkinchi atama oldingi misoldagi birinchi atama bilan bir xil. Ya'ni, raqam va raqamning hosilasi nolga teng. Ikkinchi hadning hosilasini qismning hosilasi sifatida topamiz:

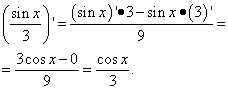
3-misol Funktsiyaning hosilasini toping

Yechim. Bu boshqa vazifa: bu erda birinchi hadda arksinus ham, boshqa trigonometrik funktsiya ham yo'q, lekin x mavjud, ya'ni bu x ning funksiyasi. Shuning uchun biz uni funktsiyalar yig'indisida atama sifatida ajratamiz:

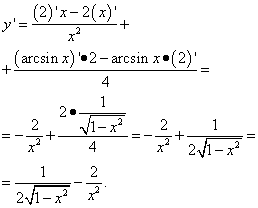
Bu erda kasrlar bilan harakatlarda, ya'ni uch qavatli kasrni yo'q qilishda ko'nikmalar talab qilindi.

4-misol Funktsiyaning hosilasini toping

Yechim. Bu erda "fi" harfi oldingi holatlarda "x" bilan bir xil rol o'ynaydi (va boshqa ko'pchilikda, lekin hammasi emas) - mustaqil o'zgaruvchi. Shuning uchun funksiyalar hosilasining hosilasini izlaganimizda, “phi” ildizining hosilasini nolga teng deb e’lon qilishga shoshilmaymiz. Shunday qilib:

Ammo yechim shu bilan tugamaydi. Shunga o'xshash a'zolar ikkita qavs ichida to'planganligi sababli, biz hali ham ifodani o'zgartirishimiz (soddalashtirishimiz) kerak. Shuning uchun biz qavslarni ulardan olingan omillarga ko'paytiramiz va keyin atamalarni umumiy maxrajga qisqartiramiz va boshqa elementar o'zgarishlarni bajaramiz:

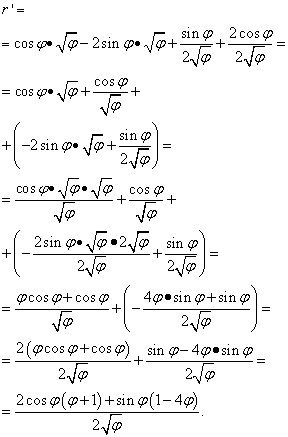
5-misol Funktsiyaning hosilasini toping

Yechim. Ushbu misolda biz shunday trigonometrik funktsiya - sekant mavjudligini va uning kosinus ko'rinishidagi formulalarini bilishimiz kerak. Farqlash:

6-misol Funktsiyaning hosilasini toping

Yechim. Ushbu misolda biz maktab kursidan ikki burchakli formulani eslab qolishimiz kerak. Lekin birinchi navbatda, farq qilaylik:

(bu ikki burchak formulasi)

Bitta o‘zgaruvchili funksiyaning differentsial hisobi

1. Kirish

Matematik tahlil- 18-asrda shakllangan va ikkita asosiy qismni o'z ichiga olgan matematikaning bo'limi: differentsial va integral hisob. Funktsiyaning hosilasi asosiy matematik tushunchalardan biridir differensial hisob. Tahlil ko'plab matematiklarning (birinchi navbatda, I. Nyuton va G. Leybnits) sa'y-harakatlari tufayli paydo bo'ldi va tabiatshunoslik rivojida ulkan rol o'ynadi - turli amaliy muammolarni hal qilishda yuzaga keladigan funktsiyalarni o'rganishning kuchli, etarlicha universal usuli. paydo bo'ldi.

2. Raqamli funktsiya. Funktsiyani o'rganish sxemasi.

("Quvvat funktsiyasi" mavzusidagi eslatmalarga qarang)

1) Funktsiya doirasi.

2) Funksiya qiymatlari to‘plami.

3) Juft, toq funksiyalar.

4) Funksiyaning monotonligi.

5) Funksiyaning qaytarilishi.

6) Funktsiya nollari.

7) Funksiyaning belgi doimiyligi intervallari.

8) Cheklangan funksiya.

Mashqlar:

Funktsiya doirasini toping:

lekin); b) ; ichida) .

lekin); b) ; G) .

3. Funksiyaning nuqtadagi chegarasi tushunchasi.

Ba'zi funktsiyalarning grafiklarini ko'rib chiqing. Keling, nuqta yaqinidagi funktsiyalarning harakatini o'rganamiz x 0 , ya'ni nuqtaning ba'zi bir mahallasida x 0 .

Guruch. 1. rasm. 2. rasm. 3.

Funksiya uni boshqa ikkita funksiyadan ajratib turuvchi xususiyatga ega.

1. Bahsga yaqinlashganda X uchun x 0 chap va o'ngda, funktsiyaning mos qiymatlari o'zboshimchalik bilan bir xil raqamga yaqin LEKIN.

Qolgan ikkita funksiya bu xususiyatga ega emas.

2. Bahsga yaqinlashganda X uchun x 0 chap tomonda, funktsiyaning tegishli qiymatlari o'zboshimchalik bilan raqamga yaqin LEKIN, va argumentga yaqinlashganda X uchun x 0 o'ng tomonda, funktsiyaning tegishli qiymatlari o'zboshimchalik bilan raqamga yaqin IN.

3. Argumentga yaqinlashganda funksiya X uchun x 0 chap va o'ng turli qiymatlarni oladi.

Chiqish: Agar argumentga yaqinlashganda X uchun x 0 chap va o'ng tomonda, koordinatali nuqtalar o'zboshimchalik bilan koordinatali nuqtaga yaqin, keyin .

Misol: Funktsiyani bajaradi x 1, x 2, x 3, x 4, x 5 nuqtalarida chegara?

Javob: Funktsiya x 1, x 3 nuqtalarida chegaraga ega;

funktsiyasi x 2, x 4, x 5 nuqtalarida chegarasi yo'q.

Izoh:

4. Nuqta va oraliqda uzluksiz funksiya ta’rifi

Funktsiyaning uzluksizligi tushunchasi ushbu funktsiyaning grafigini "uzluksiz" (qattiq) chiziq sifatidagi g'oyasi bilan qulay tarzda bog'langan. Qattiq chiziq - qalamni qog'ozdan ko'tarmasdan chizilgan chiziq.

Savol: Bu funksiyalarning qaysi biri uzluksiz?

Guruch. 1. rasm. 2. rasm. 3.

Guruch. 4. rasm. besh.

Javob: Bu funksiyalardan 1-rasmda ko'rsatilgan funksiya uzluksizdir. № 3, chunki uning grafigi "uzluksiz" (qattiq) chiziqdir.

Savol: Rasmda ko'rsatilgan funktsiyaning xususiyatlari qanday? № 3 va boshqa funktsiyalari yo'qmi?

Javob:

1. Funksiya x 0 nuqtada aniqlanadi. Bu xususiyat rasmda ko'rsatilgan funktsiyaga mos kelmaydi. № 1.

2. x 0 nuqtada funksiyaning chekli chegarasi mavjud. Bu xususiyat rasmda tasvirlangan funksiyalar uchun amal qilmaydi. № 2, 5.

3. Funksiyaning x 0 nuqtadagi chegarasi funksiyaning shu nuqtadagi qiymatiga teng, ya’ni. . Bu xususiyat rasmda ko'rsatilgan funktsiyaga mos kelmaydi. № 4.

Shaklda ko'rsatilgan funksiya uchun qanoatlantirilgan xususiyatlar. № 3 va nuqtada uzluksiz funktsiyani aniqlash imkoniyatini yarating x 0 .

Ta'rif: Funktsiya bir nuqtada uzluksiz deyiladi x 0, agar .

Izoh: Agar funktsiya bir nuqtada uzluksiz bo'lsa x 0, keyin ishora x 0 Agar funksiya nuqtada uzluksiz bo‘lmasa, funksiyaning uzluksizlik nuqtasi deyiladi x 0, keyin ishora x 0 funksiyaning uzilish nuqtasi deyiladi.

Ta'rif: Funktsiya oraliqda uzluksiz deyiladi, agar u shu oraliqning har bir nuqtasida uzluksiz bo'lsa.

5. Argument ortishi, funksiya ortishi

, funksiyasi berilsin.

x 0 - argumentning dastlabki qiymati, ;

X- argumentning yakuniy qiymati, ;

f (x 0) - funktsiyaning boshlang'ich qiymati;

f(x 0 + D x) - funksiyaning yakuniy qiymati.

Ta'rif: Argumentning yakuniy va boshlang'ich qiymatlari o'rtasidagi farq argumentning o'sishi deb ataladi. D x \u003d x - x 0

Ta'rif: Funktsiyaning yakuniy va boshlang'ich qiymatlari orasidagi farq funktsiyaning o'sishi deb ataladi. D y \u003d f (x 0 + D x) - f (x 0)

Izoh:

Argumentni geometrik ravishda oshirish D x– argumentning yakuniy va boshlang'ich qiymatlariga mos keladigan funktsiya grafigi nuqtalarining abstsissalari orasidagi farq.
Geometrik o'sish funktsiyasi D y– argumentning yakuniy va boshlang'ich qiymatlariga mos keladigan funktsiya grafigi nuqtalarining ordinatalari orasidagi farq.
Argument ortishi va funksiya ortishi ijobiy yoki salbiy boʻlishi mumkin.

6. Funksiyaning hosilasi haqida tushuncha. jismoniy ma'no hosila funksiyasi

Funktsiyaning o'zgarish tezligi masalasini ko'rib chiqing, bu erda X Va da har qanday jismoniy miqdor bo'lishi mumkin.

x 0 - argumentning dastlabki qiymati; f (x 0) - funktsiyaning boshlang'ich qiymati;

x 0 +D x - argumentning yakuniy qiymati; f(x 0 + D x) - funktsiyaning yakuniy qiymati;

D y \u003d f (x 0 + D x) - f (x 0) - funktsiyani oshirish;

– oraliqda funktsiyaning o'rtacha o'zgarish tezligi D x .

– funktsiyaning oniy o'zgarish tezligi, funktsiyaning nuqtadagi o'zgarish tezligi x 0.

Ta'rif: Funktsiyaning nuqtadagi hosilasi x 0 o'sish nisbati chegarasi deyiladi D bir nuqtada ishlaydi x 0 oshirish D x argumentning o'sishi nolga moyil bo'lganda argument.

Chiqish: Funktsiyaning nuqtadagi hosilasi x 0 nuqtadagi funksiyaning o‘zgarish tezligi x 0.

Teorema: Doimiy funktsiyaning hosilasi y = c har qanday nuqtada nolga teng.

Teorema: Funktsiyaning hosilasi y = x har qanday nuqtada birga teng .

Izoh: Berilgan funksiyaning hosilasini topish differensiallash deyiladi.

7. Funksiyalarning yig‘indisini, ko‘paytmasini, bo‘limini farqlash qoidalari

Funktsiyani ko'rib chiqing , boshqa ikkita funksiyadan iborat va intervalda hosilalarga ega:

3) .

№1 teorema: Ikki funktsiya yigʻindisining (farqining) hosilasi bu funksiyalarning hosilalari yigʻindisiga (farqiga) teng.

Misol: Funktsiyaning hosilasini hisoblang

№2 teorema: Ikki funktsiyaning hosilasi quyidagi formula bilan aniqlanadi:

Natija: O'zgarmas ko'paytmani hosilaning belgisidan chiqarish mumkin: .

Isbot: .

Misol

Mashqlar:

2) ;

Quvvat funksiyasining hosilasi quyidagi formula bilan hisoblanadi:

Izoh: Formula har qanday darajali quvvat funksiyasi uchun amal qiladi. ,

Misol: Funksiyalarning hosilalarini hisoblang:

Chiqish: .

Mashqlar: Funksiyalarning hosilalarini hisoblang:

; 2) ; 3) ;

4) ; 5) ;

6) ; 7) .

№3 teorema: Ikki funktsiya bo'limining hosilasi quyidagi formula bilan aniqlanadi:

Oqibatlari: ;

Misol: Funksiyalarning hosilalarini hisoblang:

2) . .

3) . .

Mashqlar: Funksiyalarning hosilalarini hisoblang:

1. ; 2. ; 3. ;

4. ; 5. ; 6.

;

; 8. ; 9.

8. Kompleks funksiya haqida tushuncha

Murakkab funktsiyani farqlash qoidasi

Funktsiya to'plamda va funktsiya to'plamda va uchun mos qiymat aniqlansin. Keyin to'plamda funksiya aniqlanadi, u chaqiriladi dan murakkab funktsiya X (funktsiyadan funktsiya).

O'zgaruvchiga murakkab funksiyaning oraliq argumenti deyiladi.

Misol:

Mashqlar:

Nimadan elementar funktsiyalar Ushbu murakkab funktsiyalar quyidagilardan iborat:

1) ; 2) ;

; 4) .

Ushbu elementar funksiyalardan murakkab funksiyalarni tuzing:

1) , ; 2) , ;

3) , . 4) , , .

Chiqish: Murakkab funktsiyaning hosilasi uni tashkil etuvchi elementar funksiyalarning hosilalari ko'paytmasiga teng. .

Misol: Funksiyalarning hosilalarini hisoblang:

- quvvat, chiziqli; , .

- quvvat, kvadratik; , .

Mashqlar: Funksiyalarning hosilalarini hisoblang:

1. ; 2.

;

3. ; 4. ;

; 6. .

9. Ko‘rsatkichli, logarifmik funksiyalarning hosilasi

Misol: Funksiyalarning hosilalarini hisoblang:

1. . .

2. . .

3. . .

Misol: Funksiyalarning hosilalarini hisoblang:

1. . .

2. . .

Mashqlar: Funktsiyaning hosilasini hisoblang:

1. ; 2. ; 3. ;

4. ; 5. ; 6. ;

7. ; 8. .

10. Trigonometrik funksiyalarning hosilalari

Teskari trigonometrik funksiyalarning hosilalari

Misol: Funksiyalarning hosilalarini hisoblang:

1. . .

2. . .

Vazifa

. .

Vazifa: Funktsiyaning hosilasini hisoblang.

Jismoniy mashqlar: Funktsiyaning hosilasini hisoblang.

Teskari trigonometrik funksiyalarning hosilalari

;

Mashqlar: Funksiyalarning hosilalarini hisoblang:

1. 2.

3. 4.

5. 6. 7. 8. 9.

10.

11. 12. 13.

11. geometrik ma'no hosila funksiyasi

Funktsiyani ko'rib chiqaylik.

Funksiya grafigida belgilangan nuqtani oling va ixtiyoriy nuqta . Keling, sekant chizamiz . Agar nuqta M bir nuqtaga cheksiz harakat M 0 funktsiya grafigiga ko'ra , keyin sekant M 0 M turli pozitsiyalarni egallaydi va agar nuqta mos kelsa M nuqta bilan M 0 sekant chegara pozitsiyasini egallaydi M 0 T , keyin to'g'ri chiziq M 0 T nuqtadagi funksiya grafigiga tangens bo‘ladi M 0 .

Ta'rif: Funksiya grafigiga tangens nuqtada M 0 chegara deb ataladi M 0 T sekant bir nuqtaga intilayotganda M nuqtaga jadvalga muvofiq M 0.

b- sekantning moyillik burchagi M 0 M

a- tangensning qiyalik burchagi M 0 T x o'qining musbat yo'nalishiga.

Sekantning qiyaligi M 0 M .

Tangens Nishab M 0 T .

To'g'ri uchburchakni ko'rib chiqing M 0 MA (). O'tkir burchak tangensi to'g'ri uchburchak qarama-qarshi oyoqning qo'shnisiga nisbatiga teng:

Ya'ni . Va bu degani .

Funktsiyaning nuqtadagi hosilasini aniqlang x 0 : .

, , Binobarin, .

Chiqish: Funksiya hosilasining geometrik ma’nosi shundan iboratki, at funksiyaning hosilasi abtsissa bilan nuqtada funksiya grafigiga chizilgan tangens qiyaligiga teng.

Misol:

1. Funksiya grafigiga nuqtalarda chizilgan tangensning qiyaligini toping .

; ; ; ; ; .

Javob: ; ; .

2. Funksiya grafigiga abtsissa bilan nuqtada chizilgan tangensning qiyalik burchagini toping.

; ; ; ; . to'g'ri chiziqqa parallel;

Keling, o'rnatamiz zarur shart ekstremumning mavjudligi.

Ferma teoremasi: Agar ichki nuqta bo'lsa x 0 doirasidan tashqarida uzluksiz funksiya ekstremum nuqtadir va bu nuqtada hosila mavjud, keyin u nolga teng.

Izoh: Biroq nuqtadagi funksiya hosilasining nolga tengligi x 0 hali ham buni talab qilish huquqini bermaydi x 0 – funktsiyaning ekstremum nuqtasi.

Jadvalning birinchi formulasini chiqarishda biz nuqtadagi funktsiyaning hosilasini aniqlashdan boshlaymiz. Qaerga boraylik x- har qanday haqiqiy raqam, ya'ni x– funktsiyani aniqlash maydonidan istalgan raqam . Funktsiya o'sishning argument o'sishiga nisbati chegarasini quyidagicha yozamiz:

Shuni ta'kidlash kerakki, chegara belgisi ostida nolga bo'lingan noaniqlik emas, ifoda olinadi, chunki numerator cheksiz kichik qiymatni emas, balki aniq nolni o'z ichiga oladi. Boshqacha qilib aytganda, doimiy funktsiyaning o'sishi har doim nolga teng.

Shunday qilib, doimiy funktsiyaning hosilasibutun ta'rif sohasi bo'yicha nolga teng.

Quvvat funksiyasining hosilasi.

Quvvat funksiyasining hosilasi formulasi shaklga ega , bu erda ko'rsatkich p har qanday haqiqiy sondir.

Avval natural ko‘rsatkich, ya’ni for formulasini isbotlaymiz p = 1, 2, 3, ...

Biz hosila ta'rifidan foydalanamiz. Quvvat funksiyasi ortishining argument ortishiga nisbati chegarasini yozamiz:

Numeratordagi ifodani soddalashtirish uchun Nyutonning binomial formulasiga murojaat qilamiz:

Binobarin,

Bu tabiiy daraja uchun daraja funksiyasining hosilasi formulasini isbotlaydi.

Ko'rsatkichli funktsiyaning hosilasi.

Ta'rif asosida hosila formulasini olamiz:

Noaniqlikka keldi. Uni kengaytirish uchun biz , va uchun yangi o'zgaruvchini kiritamiz. Keyin. Oxirgi o'tishda biz logarifmning yangi bazasiga o'tish uchun formuladan foydalandik.

Keling, asl chegarada almashtirishni amalga oshiramiz:

Agar ikkinchi ajoyib chegarani eslasak, eksponensial funktsiyaning hosilasi formulasiga kelamiz:

Logarifmik funktsiyaning hosilasi.

Hamma uchun logarifmik funktsiyaning hosilasi formulasini isbotlaylik x doirasidan va barcha joriy asosiy qiymatlardan a logarifm. Loyimaning ta'rifi bo'yicha bizda quyidagilar mavjud:

E'tibor berganingizdek, isbotda o'zgartirishlar logarifm xususiyatlaridan foydalangan holda amalga oshirildi. Tenglik ikkinchi ajoyib chegara tufayli amal qiladi.

Trigonometrik funksiyalarning hosilalari.

Trigonometrik funktsiyalarning hosilalari uchun formulalarni olish uchun biz ba'zi trigonometriya formulalarini, shuningdek, birinchi ajoyib chegarani esga olishimiz kerak.

Sinus funktsiyasi uchun hosilaning ta'rifiga ko'ra, biz bor .

Sinuslar farqi uchun formuladan foydalanamiz:

Birinchi ajoyib chegaraga o'tish uchun qoladi:

Demak, funktsiyaning hosilasi gunoh x yemoq chunki x.

Kosinus hosilasi formulasi ham xuddi shunday isbotlangan.

Demak, funktsiyaning hosilasi chunki x yemoq -sin x.

Tangens va kotangens uchun hosilalar jadvali formulalarini chiqarish isbotlangan differentsiallash qoidalari (kasr hosilasi) yordamida amalga oshiriladi.

Giperbolik funksiyalarning hosilalari.

Differensiallash qoidalari va hosilalar jadvalidan ko'rsatkichli funktsiya hosilasi formulasi giperbolik sinus, kosinus, tangens va kotangens hosilalari uchun formulalar chiqarish imkonini beradi.

Teskari funktsiyaning hosilasi.

Taqdimotda chalkashlik bo'lmasligi uchun, keling, pastki indeksda differentsiallash amalga oshiriladigan funktsiyaning argumentini belgilaymiz, ya'ni u funktsiyaning hosilasidir. f(x) yoqilgan x.

Endi biz shakllantiramiz teskari funksiyaning hosilasini topish qoidasi.

Funktsiyalarga ruxsat bering y = f(x) Va x = g(y) o'zaro teskari, intervallarda va mos ravishda aniqlanadi. Agar biror nuqtada funktsiyaning nolga teng bo'lmagan chekli hosilasi mavjud bo'lsa f(x), u holda nuqtada teskari funktsiyaning chekli hosilasi mavjud g(y), va . Boshqa kirishda .

Ushbu qoida har qanday kishi uchun qayta shakllantirilishi mumkin x intervaldan , keyin biz olamiz .

Keling, ushbu formulalarning to'g'riligini tekshiramiz.

Natural logarifm uchun teskari funksiya topilsin (Bu yerga y funktsiyadir va x- dalil). uchun bu tenglamani yechish x, biz olamiz (bu erda x funktsiyadir va y uning argumenti). Ya'ni, va o'zaro teskari funktsiyalar.

Hosilalar jadvalidan biz buni ko'ramiz Va .

Teskari funktsiyaning hosilalarini topish formulalari bizni bir xil natijalarga olib kelishiga ishonch hosil qilaylik:

Ko'rib turganingizdek, biz hosilalar jadvalidagi kabi natijalarga erishdik.

Endi biz teskari trigonometrik funksiyalarning hosilalari uchun formulalarni isbotlash uchun bilimga egamiz.

Arksinusning hosilasidan boshlaylik.

. Keyin, teskari funktsiyaning hosilasi uchun formula bo'yicha, biz olamiz

Transformatsiyani amalga oshirish uchun qoladi.

Arksinus diapazoni interval bo'lgani uchun , keyin (asosiy elementar funksiyalar, ularning xossalari va grafiklari bo'limiga qarang). Shuning uchun biz hisobga olmaymiz.