Numeri complessi
Immaginario e numeri complessi. Ascissa e ordinata
numero complesso. Numeri complessi coniugati.
Operazioni con numeri complessi. Geometrico
rappresentazione di numeri complessi. piano complesso.
Modulo e argomento di un numero complesso. trigonometrico
forma numerica complessa. Operazioni con complessi
numeri in forma trigonometrica. Formula Moivre.
Informazioni di base su immaginario e numeri complessi sono riportati nella sezione "Numeri immaginari e complessi". La necessità di questi numeri di un nuovo tipo è apparsa durante la risoluzione delle equazioni quadratiche per il caso
D< 0 (здесь Dè il discriminante dell'equazione quadratica). Per molto tempo questi numeri non hanno trovato uso fisico, motivo per cui sono stati chiamati numeri "immaginari". Tuttavia, ora sono ampiamente utilizzati in vari campi della fisica.e tecnologia: ingegneria elettrica, idro e aerodinamica, teoria dell'elasticità, ecc.
Numeri complessi sono scritti come:a+bi. Qui un e b – numeri reali , un io – unità immaginaria. e. io 2 = –1. Numero un chiamato ascissa, un b - ordinatanumero complessoa + b.Due numeri complessia+bi e a-bi chiamato coniugare numeri complessi.
Principali accordi:
1. Numero reale
unpuò anche essere scritto nel modulonumero complesso:un + 0 io o un - 0 io. Ad esempio, le voci 5 + 0io e 5 - 0 iosignifica lo stesso numero 5 .2. Numero complesso 0 + bichiamato puramente immaginario numero. Registrazionebisignifica uguale a 0 + bi.
3. Due numeri complessia+bi ec + disono considerati uguali sea = c e b = d. Altrimenti i numeri complessi non sono uguali.
Aggiunta. La somma dei numeri complessia+bi e c + diè chiamato numero complesso (a+c ) + (b+d ) io .In questo modo, quando aggiunto i numeri complessi, le loro ascisse e ordinate vengono sommati separatamente.
Questa definizione segue le regole per trattare i polinomi ordinari.
Sottrazione. La differenza tra due numeri complessia+bi(ridotto) e c + di(sottratto) è chiamato numero complesso (corrente alternata ) + (b-d ) io .
In questo modo, quando si sottraggono due numeri complessi, le loro ascisse e ordinate vengono sottratte separatamente.
Moltiplicazione. Il prodotto di numeri complessia+bi e c + di è chiamato numero complesso.
(ac-bd ) + (ad+bc ) io .Questa definizione nasce da due requisiti:
1) numeri a+bi e c + didovrebbe moltiplicarsi come algebrica binomi,
2) numero ioha la proprietà principale:io 2 = – 1.
ESEMPIO ( a + bi )(a-bi) = a 2 +b 2 . Di conseguenza, opera
due numeri complessi coniugati sono uguali al reale
numero positivo.
Divisione. Dividi un numero complessoa+bi (divisibile) all'altroc + di(divisore) - significa trovare il terzo numeroe + fi(chat), che, moltiplicato per un divisorec + di, che si traduce nel dividendoa + b.
Se il divisore non è zero, la divisione è sempre possibile.
ESEMPIO Trova (8+io ) : (2 – 3 io) .
Soluzione Riscriviamo questo rapporto come una frazione:
Moltiplicando numeratore e denominatore per 2 + 3io
E dopo aver eseguito tutte le trasformazioni, otteniamo:

Rappresentazione geometrica di numeri complessi. I numeri reali sono rappresentati da punti sulla linea dei numeri:
Ecco il punto UNsignifica numero -3, puntoBè il numero 2, e o- zero. Al contrario, i numeri complessi sono rappresentati da punti sul piano delle coordinate. Per questo, scegliamo coordinate rettangolari (cartesiane) con le stesse scale su entrambi gli assi. Poi il numero complessoa+bi sarà rappresentato da un punto P con ascissa a e ordinata b (vedi fig.). Questo sistema di coordinate viene chiamato piano complesso .

modulo numero complesso è chiamato lunghezza del vettoreOPERAZIONE, raffigurante un numero complesso sulla coordinata ( integrato) aereo. Modulo numerico complessoa+bi indicato da | a+bi| o lettera r
Piano di lezione.
1. Momento organizzativo.
2. Presentazione del materiale.
3. Compiti a casa.
4. Riassumendo la lezione.
Durante le lezioni
I. Momento organizzativo.
II. Presentazione del materiale.
Motivazione.
L'espansione dell'insieme dei numeri reali consiste nel fatto che ai numeri reali vengono aggiunti nuovi numeri (immaginari). L'introduzione di questi numeri è connessa con l'impossibilità di estrarre la radice da un numero negativo nell'insieme dei numeri reali.
Introduzione del concetto di numero complesso.
I numeri immaginari con cui integriamo i numeri reali si scrivono come bi, dove ioè l'unità immaginaria, e io 2 = - 1.
Sulla base di ciò, otteniamo la seguente definizione di numero complesso.
Definizione. Un numero complesso è un'espressione della forma a+bi, dove un e b sono numeri reali In questo caso sono soddisfatte le seguenti condizioni:
a) Due numeri complessi a 1 + b 1 i e a 2 + b 2 i uguale se e solo se un 1 = un 2, b1=b2.
b) L'addizione di numeri complessi è determinata dalla regola:
(un 1 + b 1 io) + (un 2 + b 2 io) = (un 1 + un 2) + (b 1 + b 2) io.
c) La moltiplicazione dei numeri complessi è determinata dalla regola:
(un 1 + b 1 i) (un 2 + b 2 i) = (un 1 un 2 - b 1 b 2) + (un 1 b 2 - un 2 b 1) io.
Forma algebrica di un numero complesso.
Scrivere un numero complesso nella forma a+biè detta forma algebrica di un numero complesso, dove un- parte reale biè la parte immaginaria, e bè un numero reale
Numero complesso a+biè considerato uguale a zero se le sue parti reale e immaginaria sono uguali a zero: a=b=0
Numero complesso a+bi a b = 0 considerato un numero reale un: a + 0i = a.
Numero complesso a+bi a a = 0è chiamato puramente immaginario ed è indicato bi: 0 + bi = bi.
Due numeri complessi z = a + bi e = a – bi, che differiscono solo per il segno della parte immaginaria, sono detti coniugati.
Azioni su numeri complessi in forma algebrica.
Le seguenti operazioni possono essere eseguite su numeri complessi in forma algebrica.
1) Aggiunta.
Definizione. La somma dei numeri complessi z 1 = un 1 + b 1 io e z 2 = un 2 + b 2 io chiamato un numero complesso z, la cui parte reale è uguale alla somma delle parti reali z1 e z2, e la parte immaginaria è la somma delle parti immaginarie dei numeri z1 e z2, questo è z = (un 1 + un 2) + (b 1 + b 2)i.
Numeri z1 e z2 sono chiamati termini.
L'addizione di numeri complessi ha le seguenti proprietà:
1º. Commutatività: z1 + z2 = z2 + z1.
2º. Associatività: (z 1 + z 2) + z 3 = z 1 + (z 2 + z 3).
3º. Numero complesso -a -biè chiamato il contrario di un numero complesso z = a + bi. Numero complesso opposto al numero complesso z, indicato -z. Somma di numeri complessi z e -zè uguale a zero: z + (-z) = 0
Esempio 1: aggiungi (3 - i) + (-1 + 2 i).
(3 - i) + (-1 + 2i) = (3 + (-1)) + (-1 + 2) i = 2 + 1i.
2) Sottrazione.
Definizione. Sottrai dal numero complesso z1 numero complesso z2 z, che cosa z + z 2 = z 1.
Teorema. La differenza dei numeri complessi esiste e, inoltre, è unica.
Esempio 2: Sottrai (4 - 2i) - (-3 + 2i).
(4 - 2i) - (-3 + 2i) = (4 - (-3)) + (-2 - 2) i = 7 - 4i.
3) Moltiplicazione.
Definizione. Il prodotto di numeri complessi z 1 =a 1 +b 1 io e z 2 \u003d a 2 + b 2 i chiamato un numero complesso z, definito dall'uguaglianza: z = (a 1 a 2 – b 1 b 2) + (a 1 b 2 + a 2 b 1)i.
Numeri z1 e z2 sono chiamati fattori.
La moltiplicazione di numeri complessi ha le seguenti proprietà:
1º. Commutatività: z 1 z 2 = z 2 z 1.
2º. Associatività: (z 1 z 2)z 3 = z 1 (z 2 z 3)
3º. Distributività della moltiplicazione rispetto all'addizione:
(z 1 + z 2) z 3 \u003d z 1 z 3 + z 2 z 3.
4º. z \u003d (a + bi) (a - bi) \u003d a 2 + b 2è un numero reale
In pratica la moltiplicazione dei numeri complessi avviene secondo la regola di moltiplicare la somma per la somma e separare la parte reale da quella immaginaria.
Nell'esempio seguente, considera la moltiplicazione di numeri complessi in due modi: per la regola e moltiplicando la somma per la somma.
Esempio 3: Moltiplica (2 + 3i) (5 – 7i).
1 via. (2 + 3i) (5 – 7i) = (2× 5 – 3× (- 7)) + (2× (- 7) + 3× 5)i = = (10 + 21) + (- 14 + 15 )i = 31 + io.
2 vie. (2 + 3i) (5 - 7i) = 2× 5 + 2× (- 7i) + 3i× 5 + 3i× (- 7i) = = 10 - 14i + 15i + 21 = 31 + i.
4) Divisione.
Definizione. Dividi un numero complesso z1 ad un numero complesso z2, significa trovare un numero così complesso z, che cosa z z 2 = z 1.
Teorema. Il quoziente dei numeri complessi esiste ed è unico se z2 ≠ 0 + 0i.
In pratica il quoziente dei numeri complessi si trova moltiplicando numeratore e denominatore per il coniugato del denominatore.
Permettere z 1 = un 1 + b 1 io, z 2 = un 2 + b 2 io, poi



 .
.
Nell'esempio seguente, eseguiamo la divisione per la formula e la regola della moltiplicazione per il coniugato del denominatore.
Esempio 4. Trova un quoziente  .
.
5) Elevazione a potenza intera positiva.
a) Poteri dell'unità immaginaria.
Approfittando dell'uguaglianza io 2 \u003d -1, è facile definire qualsiasi potenza intera positiva dell'unità immaginaria. Abbiamo:
io 3 \u003d io 2 io \u003d -i,
io 4 \u003d io 2 io 2 \u003d 1,
io 5 \u003d io 4 io \u003d io,
io 6 \u003d io 4 io 2 \u003d -1,
io 7 \u003d io 5 io 2 \u003d -i,
io 8 = io 6 io 2 = 1 eccetera.
Questo mostra che i valori di grado in, dove n- un numero intero positivo, ripetuto periodicamente all'aumentare dell'indicatore 4 .
Pertanto, per aumentare il numero io a una potenza intera positiva, dividere l'esponente per 4 ed eretto io alla potenza il cui esponente è il resto della divisione.
Esempio 5 Calcola: (io 36 + io 17) io 23.
io 36 = (io 4) 9 = 1 9 = 1,
io 17 = io 4 × 4+1 = (io 4) 4 × io = 1 io = io.
io 23 = io 4 × 5+3 = (io 4) 5 × io 3 = 1 io 3 = - io.
(io 36 + io 17) io 23 \u003d (1 + i) (- i) \u003d - io + 1 \u003d 1 - i.
b) L'elevazione di un numero complesso a una potenza intera positiva si effettua secondo la regola di elevare un binomio alla potenza corrispondente, poiché si tratta di un caso speciale di moltiplicazione di fattori complessi identici.
Esempio 6 Calcola: (4 + 2i) 3
(4 + 2i) 3 = 4 3 + 3× 4 2 × 2i + 3× 4× (2i) 2 + (2i) 3 = 64 + 96i – 48 – 8i = 16 + 88i.
I numeri complessi sono un'estensione minima dell'insieme dei numeri reali a noi familiari. La loro differenza fondamentale è che appare un elemento che al quadrato dà -1, cioè io, o .
Ogni numero complesso ha due parti: reale e immaginario:
Pertanto, è chiaro che l'insieme dei numeri reali coincide con l'insieme dei numeri complessi con parte immaginaria zero.
Il modello più popolare per l'insieme dei numeri complessi è il piano ordinario. La prima coordinata di ogni punto sarà la sua parte reale e la seconda immaginaria. Quindi il ruolo dei numeri complessi stessi sarà vettori con l'inizio nel punto (0,0).
Operazioni sui numeri complessi.
Infatti, se prendiamo in considerazione il modello dell'insieme dei numeri complessi, è intuitivamente chiaro che l'addizione (sottrazione) e la moltiplicazione di due numeri complessi vengono eseguite allo stesso modo delle corrispondenti operazioni sui vettori. Inoltre, intendiamo il prodotto incrociato dei vettori, perché il risultato di questa operazione è ancora un vettore.
1.1 Aggiunta.
(Come puoi vedere, questa operazione corrisponde esattamente a )
1.2 Sottrazione, analogamente, viene eseguita secondo la seguente regola:
2. Moltiplicazione.

3. Divisione.
È definito semplicemente come l'operazione inversa della moltiplicazione.

forma trigonometrica.
Il modulo di un numero complesso z è la seguente quantità:
 ,
,
è ovvio che questo, ancora, è semplicemente il modulo (lunghezza) del vettore (a,b).
Molto spesso, il modulo di un numero complesso è indicato come ρ.
Si scopre che
z = ρ(cosφ+isinφ).

Quanto segue segue direttamente dalla forma trigonometrica di scrivere un numero complesso. formule :
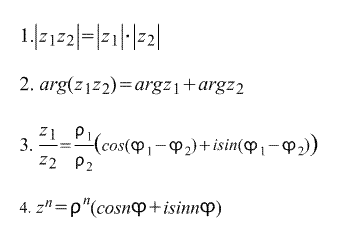
Viene chiamata l'ultima formula Formula di De Moivre. La formula è derivata direttamente da essa. radice n-esima di un numero complesso:

quindi, ci sono n ennesima radice del numero complesso z.