Az alábbiakban a problémák feltételeit és a szkennelt megoldásokat ismertetjük. Ha meg kell oldania egy problémát ebben a témában, itt találhat egy hasonló feltételt, és analógia útján oldja meg a sajátját. Az oldal betöltése eltarthat egy ideig a képek nagy száma miatt. Ha problémamegoldásra vagy online segítségre van szüksége fizikában, keressen minket, szívesen segítünk.

E problémák megoldásának elve az, hogy egy szabadon eső test sebességét két komponensre - vízszintesre és függőlegesre - bontják. A sebesség vízszintes összetevője állandó, a függőleges mozgás a szabadesés g=9,8 m/s 2 gyorsulásával történik. Alkalmazható a mechanikai energia megmaradásának törvénye is, amely szerint a test potenciális és mozgási energiájának összege ebben az esetben állandó.

Egy anyagi pontot 15 m/s kezdeti sebességgel a horizonthoz képest szögben dobnak. A kezdeti kinetikus energia 3-szor nagyobb, mint a pálya felső pontjában lévő pont kinetikus energiája. Milyen magasra emelkedett a pont?

Egy testet a vízszinteshez képest 40 fokos szögben dobnak 10 m/s kezdeti sebességgel. Határozza meg azt a távolságot, amelyet a test repül a zuhanás előtt, az emelkedés magasságát a pálya felső pontjában és a repülési időt.

Egy testet vetünk le a H magasságú toronyból, a vízszinteshez képest α szögben, v kezdősebességgel. Keresse meg a távolságot a torony és a hely között, ahol a test leesett.

Egy 0,5 kg tömegű testet a Föld felszínéről a vízszinteshez képest 30 fokos szögben, 10 m/s kezdeti sebességgel dobnak ki. Határozza meg a test potenciális és kinetikus energiáit 0,4 s után!

Egy anyagi pontot a Föld felszínéről a horizonthoz képest szögben felfelé dobnak 10 m/s kezdeti sebességgel. Határozzuk meg egy 3 m magasságban lévő pont sebességét!

Egy testet 60 fokos szögben felfelé dobnak a Föld felszínéről 10 m/s kezdeti sebességgel. Határozza meg az ütközési pont távolságát, a test sebességét az ütközési pontban és a repülési időt.

Egy testet a vízszinteshez képest szögben felfelé dobnak 20 m/s kezdeti sebességgel. Az esési pont távolsága a maximális emelési magasság 4-szerese. Keresse meg azt a szöget, amelybe a testet bedobják.

Egy testet 5 m magasságból a vízszinteshez képest 30 fokos szögben dobnak ki 22 m/s kezdeti sebességgel. Határozza meg a test repülési hatótávolságát és a test repülési idejét!

Egy testet 30 m/s kezdeti sebességgel dobnak ki a Föld felszínéről a horizonthoz képest szögben. Határozza meg a test tangenciális és normál gyorsulását 1 másodperccel a dobás után!

A Zesli felszínéről a vízszinteshez képest 30 fokos szögben egy testet dobnak ki 14,7 m/s kezdeti sebességgel. Határozza meg a test tangenciális és normál gyorsulását 1,25 másodperccel a dobás után!

Egy testet a vízszinteshez képest 60 fokos szögben dobnak 20 m/s kezdeti sebességgel. Mennyi idő múlva lesz a sebesség és a horizont szöge 45 fok?

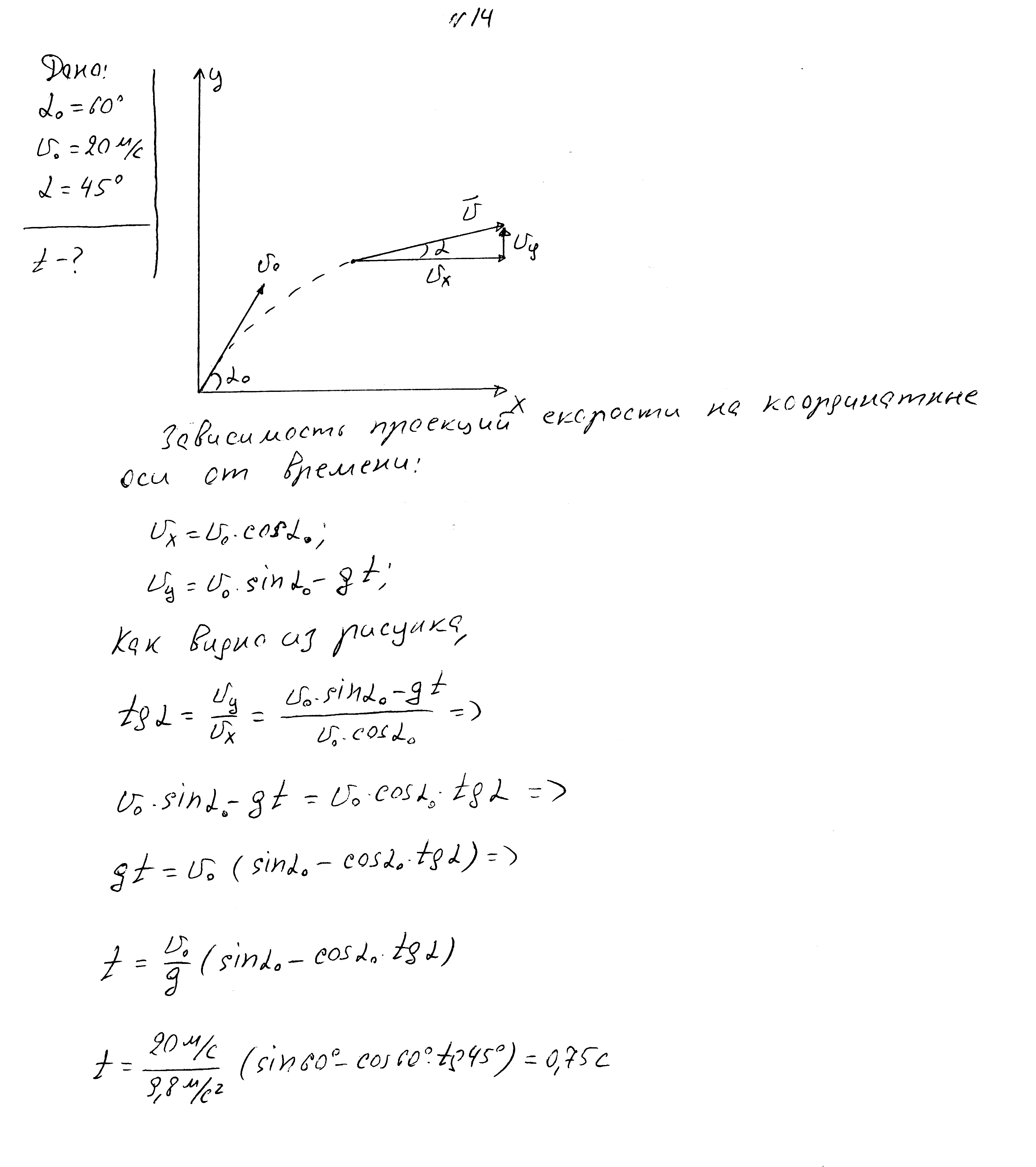
Dobott labda az edzőteremben a horizonthoz képest szögben,20 m/s kezdeti sebességgel a pálya felső pontján 8 m magasságban a mennyezetet érintette és a dobás helyétől bizonyos távolságra leesett. Határozza meg ezt a távolságot és azt a szöget, amelyen a test el van vetve.

A Föld felszínéről a horizonthoz képest szögben kidobott test 2,2 s után leesett. Keresse meg a test maximális emelési magasságát.

Egy követ a vízszinteshez képest 30 fokos szögben dobnak. A kő kétszer ért el egy bizonyos magasságot – 1 és 3 másodperccel az eldobás után. Határozza meg ezt a magasságot és a kő kezdeti sebességét.

Egy követ a vízszinteshez képest 30 fokos szögben dobnak 10 m/s kezdeti sebességgel. Határozza meg a dobási pont és a kő távolságát 4 s után.

A lövedéket abban a pillanatban sütötték ki, amikor a gép a látóhatárhoz képest szögben 500 m/s kezdeti sebességgel átrepül a fegyver fölött. A lövedék 10 másodperccel a kilövés után 3,5 km-es magasságban érte a gépet. Mekkora a repülőgép sebessége?

Egy 5 kg tömegű ágyúgolyót dobnak ki a Föld felszínéről a vízszinteshez képest 60 fokos szögben. A tömeg felgyorsítására fordított energia 500 J. Határozza meg a repülési távolságot és a repülési időt.

Egy testet 100 m magasságból a vízszinteshez képest 30 fokos szögben 5 m/s kezdeti sebességgel dobnak le. Keresse meg a test repülési hatótávját.

Egy 200 g tömegű, a Föld felszínéről a horizonthoz képest szögben kidobott test 1,2 másodperc múlva 5 m távolságra esett. Keress egy testdobó munkát.

Legyen egy test a vízszintessel α szöget bezárva sebességgel. A korábbi esetekhez hasonlóan a légellenállást figyelmen kívül hagyjuk. A mozgás leírásához két koordinátatengelyt kell kiválasztani - Ox és Oy (29. ábra).

29. ábra

A referenciapont kompatibilis a test kezdeti helyzetével. A kezdősebesség vetületei Oy és Ox tengelyekre: , . Gyorsulási előrejelzések: ,

Ekkor a test mozgását a következő egyenletek írják le:

(8)

(9)

Ezekből a képletekből az következik, hogy vízszintes irányban a test egyenletesen, függőlegesen pedig egyenletesen gyorsulva mozog.

A test pályája egy parabola lesz. Figyelembe véve, hogy a parabola legfelső pontján megtalálhatjuk azt az időt, amely alatt a test felemelkedik a parabola felső pontjára:

A t 1 értékét a (8) egyenletbe behelyettesítve megkapjuk a test maximális magasságát:

A test maximális emelési magassága.

A test repülési idejét abból a feltételből kapjuk, hogy t=t 2-nél az y 2 =0 koordináta. Ennélfogva, . Ezért - a test repülési ideje. Összehasonlítva ezt a képletet a (10) képlettel, azt látjuk, hogy t 2 =2t 1.

A test mozgási ideje a maximális magasságból t 3 =t 2 -t 1 =2t 1 -t 1 =t 1. Következésképpen az az idő, ami alatt egy test felemelkedik a maximális magasságára, ugyanannyi időbe telik, hogy erről a magasságról leereszkedjen. A t 2 időértéket behelyettesítve a (6) x koordináta egyenletbe, azt kapjuk:

- testrepülési távolság.

A pillanatnyi sebesség a pálya bármely pontjában érintőlegesen irányul a pályára (lásd 29. ábra), a sebességmodult a képlet határozza meg

Így a horizonttal szögben vagy vízszintes irányban elhajított test mozgása két független mozgás - vízszintes egyenletes és függőleges egyenletesen gyorsított (szabadesés kezdősebesség nélkül vagy függőlegesen eldobott test mozgása) eredményének tekinthető. emelkedő).

Nézzük meg, mi lehet a kinematikai problémák célja.

1. Érdekelhet bennünket a kinematikai mennyiségek változása mozgás folyamata, azaz információk beszerzése a koordináták változásairól, a sebességről, a gyorsulásról, valamint a megfelelő szögértékekről.

2. Számos probléma esetén, például egy test horizonttal szögben történő mozgásának problémájában meg kell tanulni a fizikai mennyiségek értékeit speciális feltételek: repülési távolság, maximális emelés stb.

3. Azokban az esetekben, amikor egy test egyidejűleg több mozgásban vesz részt (például egy golyó gurítása), vagy több test egymáshoz viszonyított mozgását vesszük figyelembe, szükségessé válik az elmozdulások, a sebességek és a gyorsulások (lineáris és szögletes) közötti összefüggések megállapítása. azaz egyenleteket találni kinematikai kapcsolat.

A kinematikai problémák sokfélesége ellenére megoldásukra a következő algoritmus javasolható:

1. Készítsen vázlatos rajzot, ábrázolva a testek kiindulási helyzetét és azok kezdeti állapotát, i.e. És .

2. Válassza ki a referenciarendszert a problémakörülmények elemzése alapján. Ehhez ki kell választani egy referenciatestet, és hozzá kell rendelni egy koordinátarendszert, amely jelzi a koordináták origóját, a koordinátatengelyek irányát és az időreferencia kezdetének pillanatát. A pozitív irányok kiválasztásakor a mozgás iránya (sebesség) vagy a gyorsulás iránya vezérli őket.

3. A mozgástörvények alapján alkosson egyenletrendszert vektor alakban minden testre, majd skaláris alakban, vetítve ezeket a vektoros mozgásegyenleteket a koordinátatengelyekre! Ezen egyenletek felírásakor ügyelni kell a bennük szereplő vektormennyiségek vetületeinek „+” és „-” jeleire.

4. A választ elemző képlet formájában (általános formában) kell megkapni, majd a végén numerikus számításokat kell végezni.

4. példa Meddig lát egy 54 km/h sebességgel haladó vonat ablakánál ülő utas egy közeledő vonatot, melynek sebessége 36 km/h, hossza 250 m?

Megoldás. A rögzített vonatkoztatási rendszert a Földdel fogjuk összekötni, a mozgó keretet pedig azzal a vonattal, amelyben az utas tartózkodik. A sebességek összeadásának törvénye szerint hol van a szembejövő vonat sebessége az elsőhöz képest. Az ökör tengelyére vetítve:

Mivel a szembejövő vonat által megtett út az elsőhöz képest megegyezik a vonat hosszával, akkor az idő

5. példa A gőzös Nyizsnyij Novgorodból Asztrahánba 5,0, visszafelé pedig 7,0 napig tart. Mennyi ideig tart a tutaj Nyizsnyij Novgorodból Asztrahánba? Kerülje a parkolást és a forgalom késését.

Adott: t 1 =5 nap, t 2 =7 nap.

Megoldás. A rögzített vonatkoztatási rendszert a parttal, a mozgót a vízzel fogjuk összekötni. Feltételezzük, hogy a víz sebessége a teljes út során azonos, és a gőzhajó vízhez viszonyított sebessége állandó, és egyenlő a gőzhajó vízhez viszonyított pillanatnyi sebességének modulusával.

Mivel a tutaj a parthoz képest a folyó áramlási sebességével mozog, ezért mozgásának ideje , ahol s a városok közötti távolság. Amikor egy gőzhajó az árammal együtt mozog, a sebessége a sebességek összeadásának törvénye szerint, vagy az Ox tengelyére vetítve:

ahol a hajó sebessége a parthoz képest, a hajó sebessége a folyóhoz képest.

A mozgási idő ismeretében megtalálhatja a sebességet:

Az (1) és (2) képletből a következőket kapjuk:

Amikor a hajó az árammal szemben mozog, vagy az ökör tengelyére vetítve, hol a hajó sebessége a parthoz képest.

A másik oldalon, . Akkor

Megoldva a (3) és (4) egyenletrendszert, kapjuk:

Keressük a tutaj mozgási idejét:

6. példa. Egyenletesen gyorsított mozgásnál a test az első két egyenlő egymást követő időszakban, egyenként 4,0 s-ot halad, az s 1 = 24 m, illetve az s 2 = 64 m utak mentén. Határozza meg a test kezdeti sebességét és gyorsulását!

Adott: t 1 =t 2 = 4,0 s, s 1 = 24 m, s 2 = 64 m.

Megoldás.Írjuk fel az s 1 és (s 1 + s 2) útvonalegyenleteit. Mivel a kezdeti sebesség ebben az esetben ugyanaz, akkor

Mivel t1=t2, akkor

Kifejezve (1)-ből és behelyettesítve (2-be) a következőt kapjuk:

Aztán a kezdeti sebesség

7. példa. Egyenesen 5,0 m/s kezdősebességgel gyorsított egyenes úton haladó autó az első másodpercben 6,0 m távolságot tett meg. Határozza meg az autó gyorsulását, a pillanatnyi sebességet a második másodperc végén és a elmozdulás 2,0 s alatt.

Megoldás. A test által az első másodpercben megtett út ismeretében megtalálhatja a gyorsulást:

A képlet segítségével megtaláljuk a sebességet a második másodperc végén

8. példa. x) alakja x = A + Bt + Ct 3, ahol A = 4 m, B = 2 m/s, C = -0,5 m/s 3.

A t 1 =2 s időpillanathoz határozza meg: 1) a pont koordinátáját x 1 pont; 2) pillanatnyi sebesség v 1; 3) azonnali gyorsulás egy 1.

Adott: x = A + Bt + Ct 3, A = 4 m, B = 2 m/s, C = -0,5 m/s 3, t 1 = 2 s.

Keresse meg: x 1 ; v 1; egy 1.

Megoldás. 1. Helyettesítsük be t helyett a mozgásegyenletbe a megadott t 1 időértéket: x 1 = A + Bt 1 + Ct 1 3. Helyettesítsük be az A, B, C, t 1 értékeket ebbe a kifejezésbe, és végezzük el a számításokat: x 1 = 4 m.

2. Pillanatnyi sebesség: Ekkor t 1 időpontban a pillanatnyi sebesség v 1 = B + 3Ct 1 2 . Helyettesítsük itt a B, C, t 1 értékeit: v 1 = – 4 m/s. A mínusz jel azt jelzi, hogy t 1 =2 s időpontban a pont a koordinátatengely negatív irányába mozog.

3. Azonnali gyorsulás: A pillanatnyi gyorsulás t 1 időpontban egyenlő a 1 = 6Сt 1 értékkel. Helyettesítsük be C, t 1 értékeit: a 1 = –6 m/s 2. A mínusz jel azt jelzi, hogy a gyorsulásvektor iránya egybeesik a koordináta tengelyének negatív irányával, és ennek a feladatnak a feltételei között ez az idő bármely pillanatában bekövetkezik.

9. példa. Egy anyagi pont egyenes (tengely) mentén történő mozgásának kinematikai egyenlete x) alakja x = A + Bt + Ct 2, ahol A = 5 m, B = 4 m/s, C = -1 m/s 2. Határozza meg a v xsr átlagos sebességet a t 1 =1 s és t 2 =6 s közötti időintervallumra.

Adott: x = A + Bt + Ct 2, A = 5 m, B = 4 m/s, C = - 1 m/s 2, t 1 = 1 s, t 2 = 6 s.

Keresés: v xsr -? és khsr -?

Megoldás. Az átlagos sebességet a t 2 -t 1 időintervallumban a v cf = (x 2 - x 1)/(t 2 - t 1) kifejezés határozza meg.

x 1 = A + Bt 1 + Ct 1 2 = 8 m, x 2 = A + Bt 2 + Ct 2 2 = –7 m.

Helyettesítsük be az x 1, x 2, t 1, t 2 értékeket, és végezzük el a számításokat: v xsr = -3 m/s.

10. példa. A h = 300 m magasságban elhelyezkedő helikopterről rakományt ejtettek le. Mennyi idő alatt éri el a rakomány a földet, ha: a) a helikopter áll; b) a helikopter v 0 =5 m/s sebességgel ereszkedik le; 3) a helikopter v 0 =5 m/s sebességgel emelkedik. Írja le grafikusan a terhelés megfelelő mozgásait az s(t), v(t) és a(t) tengelyeken!

Megoldás. a) Az álló helikoptert elhagyó rakomány szabadon esik, azaz. egyenletesen mozog a gravitációs gyorsulással g. A mozgás idejét a From relációból fogjuk megtalálni: A tárgymozgások grafikonjait 1-gyel jelöltük az ábrán.

b) A helikoptert elhagyó, állandó v 0 = 5 m/s sebességgel ereszkedő rakomány mozgása egyenletesen gyorsuló mozgás, állandó g gyorsulással, és az egyenlet írja le.

A számértékeket behelyettesítve a 9.8t 2 +10t-600=0 egyenletet kapjuk.

A negatív eredménynek nincs fizikai jelentése, így a mozgási idő t=7,57 s.

A tárgymozgások grafikonjait 2-vel jelöltük az ábrán.

3) A helikopterből kilépő rakomány mozgása, amely v 0 =5 m/s állandó sebességgel emelkedik, két szakaszból áll. Az első szakaszban a terhelés egyenletesen lassan, állandó g gyorsulással, a sebességgel ellentétes irányban mozog, és az egyenletek írják le

A pálya legfelső pontján a sebesség nullává válik, tehát

A rendszer második egyenletét behelyettesítve az elsőbe, azt kapjuk

A második szakaszban - szabadesés h 0 =h+h 1 =300+1,28=301,28 m magasságból.

Mert a

Az ábrán a tárgyak mozgásának grafikonjait 3-mal jelöltük.

11. példa. A 2 m/s állandó sebességgel, a talajhoz képest 18 m/s sebességgel ereszkedő ballonról függőlegesen felfelé teher vetődik. Határozza meg a labda és a teher közötti távolságot abban a pillanatban, amikor a terhelés eléri emelkedése legmagasabb pontját. Mennyi ideig tart, amíg a rakomány elrepül a labda mellett és leesik?

Adott: v 01 = 2 m/s, v 02 = 18 m/s

Keresés: s-? τ -?

Megoldás. Irányítsuk a 0Y tengelyt függőlegesen felfelé, az origó kompatibilis a 0 ponttal, ahol a labda a teherfeldobás pillanatában volt.

Ekkor a rakomány és a ballon mozgásegyenlete:

A teher mozgási sebessége a törvény szerint változik v 2 = v 02 – gt.

A teheremelés legmagasabb B pontján v 2 =0. Ezután az emelkedési idő ehhez a ponthoz A terhelés koordinátája a B pontban

Ezalatt a léggömb leereszkedett az A pontba; annak koordinátája

Az A és B pont közötti távolság:

Egy τ idő elteltével, amikor a kő elrepül a labda mellett, a testek koordinátái ugyanazok lesznek: y 1C = y 2C;

12. példa. Milyen sebességgel és milyen irányban repüljön egy repülőgép, hogy két óra alatt 300 km-t észak felé repüljön, ha repülés közben a délkörhöz képest 30°-os szögben északnyugati szél fúj, 27 km/h sebességgel?

Adott: t=7,2∙10 3 s; l=3∙10 5 m; α=30° ≈ 0,52 rad; v 2 ≈7,2 m/s.

Keresés: v 2 -? φ -?

Megoldás. Tekintsük egy repülőgép mozgását a talajhoz viszonyított vonatkoztatási keretben.

Rajzoljuk az OX tengelyt keleti, az OY tengelyt északi irányba. Ezután a repülőgép sebessége a kiválasztott referenciakeretben

ahol v= l/t (2)

Az (1) egyenlet a tengelyre vetítésben

OX: 0=v 1 ∙sinα – v 2 ∙sinφ;

OY: v= v 2 ∙cosφ - v 1 ∙cosα, vagy v 1 ∙sinα = v 2 ∙sinφ, v 2 ∙cosφ=v 1 ∙cosα + v (3)

Ha ezeket az egyenleteket tagokkal osztjuk, megkapjuk a tanφ=v 1 sinα/(v 1 cosα+ v),

vagy figyelembe véve (2)

tgφ=v 1 ∙sinα/(v 1 ∙cosα+ l/t);

φ=arctgv 1 ∙sinα/(v 1 ∙cosα+ l/t) ≈0,078 rad.

A (3) egyenlet jobb és bal oldalát négyzetre emelve és a kapott egyenleteket összeadva azt kapjuk,

v 2 2 ∙sin 2 φ + v 2 2 ∙cos 2 φ = v 1 2 sin 2 α+ (v 1 ∙cosα + v) 2,

honnan , vagy figyelembe véve (2)

13. példa. A függőlegesen felfelé dobott test t=3 s után visszatér a talajra. Határozza meg a test emelkedési magasságát és kezdeti sebességét.

Megoldás. A test felfelé mozgása ugyanolyan lassú és gyors, gés idővel megtörténik t 1, és a lefelé irányuló mozgás egyenletesen gyorsul g gyorsulással, és idővel következik be t 2. Az AB és BA szakaszok mozgását leíró egyenletek egy rendszert alkotnak:

Mivel v B =0, akkor v 0 =gt 1. A rendszer első egyenletébe v 0-t behelyettesítve megkapjuk. Ha ezt a kifejezést összehasonlítjuk a rendszer harmadik egyenletével, akkor megállapíthatjuk, hogy az emelkedési idő megegyezik a t 1 =t 2 =t/2=1,5 s süllyedési idővel. A kezdeti sebesség és a leszállási sebesség megegyezik egymással, és összege v 0 =v A =gt 1 =9,8∙1,5=14,7 m/s.

Test emelési magassága

14. példa. A mozgás utolsó másodpercében egy szabadon zuhanó test meghaladta a távolság felét. Keresse meg azt a magasságot, ahonnan eldobta, és a mozgás idejét.

Megoldás. A megtett távolság időfüggősége szabadon eső test esetén. Mivel a teljes út felét kitevő BC szakaszt 1 s idő alatt tettük meg, így az AB út első felét (t-1) s idő alatt tettük meg. Ekkor a repülőgép-szakasz mozgását a következőképpen írhatjuk le.

A rendszer megoldása

t 2 -4t+2=0 kapjuk. Ennek az egyenletnek a gyöke: t 1 =3,41 s és t 2 =0,59 s. A második gyökér nem alkalmas, mert a mozgási időnek a probléma körülményei alapján meg kell haladnia az egy másodpercet. Következésképpen a test 3,41 másodpercig esett, és ezalatt egy távolságot tett meg

15. példa. Egy 25 m magas toronyból vízszintesen követ dobnak ki 15 m/s sebességgel.

Keresse meg: 1) mennyi ideig lesz mozgásban a kő, 2) milyen távolságra esik a földre, 3) milyen sebességgel zuhan a földre, 4) milyen szöget zár be a kő pályája a a horizont a földre zuhanás pontján. A légellenállás figyelmen kívül hagyása.

Adott: H=25 m, v o =15 m/s

Keresés: t-? s x - ? v - ? φ-?

Megoldás. A vízszintesen dobott kő mozgása két részre bontható: vízszintesre s xés függőleges s y:

ahol t a mozgás ideje.

2) s x = v o t = 33,9 m;

3) v y =gt = 22,1 m/s;

4) sinφ= v y/v=0,827;

16. példa. Egy testet vízszintesen kidobnak egy 25 m magas toronyból v x = 10 m/s sebességgel.

Keresse meg: 1) a test esésének t idejét, 2) milyen távolságra l a torony tövéből le fog esni, 3) v sebességet az esés végén, 4) azt a szöget, amelyet a test pályája bezár a talajjal a leszállási ponton.

Megoldás. A testmozgás összetett. Vízszintesen egyenletes, függőlegesen g gyorsulással egyenletesen gyorsított mozgásban vesz részt. Ezért az AB szakaszt a következő egyenletek írják le:

Az A pont esetében ezek az egyenletek a következőképpen alakulnak:

Akkor l=10∙2,26=22,6 m, és v y =9,8∙2,26=22,15 m/s.

Azóta

A pálya által a talajjal bezárt szög egyenlő az A pontban lévő sebességháromszög φ szögével, amelynek érintője , ezért φ=68,7°.

17. példa. Egy v x =10 m/s vízszintes sebességgel dobott testre a mozgás megkezdése utáni t=2 s idő után keresse meg: normál, érintőleges és teljes gyorsulást, valamint a pálya görbületi sugarát ezen a ponton.

Megoldás. Függőleges sebességkomponens v y =gt=9,8∙2=19,6 m/s

Sebesség az A pontban:

A vektorok a sebességek háromszögét, a vektorok pedig a gyorsulások háromszögét alkotják. Amint az ábrán látható, ezek a háromszögek hasonlóak, ami azt jelenti, hogy oldalaik arányosak: .

Normál gyorsulás, tehát a pálya görbületi sugara

18. példa. Egy labdát 10 m/s sebességgel dobnak a vízszinteshez képest 40°-os szögben.

Keresse meg: 1) milyen magasságba emelkedik a labda; 2) milyen távolságra esik a labda a földre a dobás helyétől, 3) mennyi ideig lesz mozgásban.

Adott: v o =10 m/s, α=40 o.

Keresés: s y - ? s x - ? t - ?

Megoldás. 1) Határozzuk meg azt a legnagyobb s y max magasságot, amelyre a horizonttal α szögben v o sebességgel dobott test felemelkedik. Nálunk van (lásd az ábrát):

v y =v o sinα – gt; (1)

s y =v o t∙sinα – gt 2 /2. (2)

A legfelső pontban v y = 0 és (1)-ből v o ∙sin𝛼 = gt 1 , ebből a labda felemelésének ideje t 1 =v o ∙sinα/g. Ha t 1-et (2) behelyettesítünk, azt kapjuk

s y max = v o 2 ∙sin 2 α/(2g)= 2,1 m.

2) Határozza meg a horizonttal szögben elhajított test s x max repülési távolságát!

Van: v x =v o∙cosα , (3)

s x =v x t=v o t∙cosα. (4)

A test a t 2 =2t 1 =2v o sinα/g idő után vízszintes síkra esik.

Ha t 2-t (4) behelyettesítünk, akkor s xmax = v o 2 sin2α/ g= 10,0 m.

3) t 2 =2t 1 =2v o sinα/g=1,3 s.

19. példa. Egy testet v 0 =10 m/s 2 sebességgel a vízszinteshez képest α=30°-os szögben dobnak. Milyen magasságba emelkedik a test? Mekkora távolságra éri a földet a dobás helyétől? Meddig lesz mozgásban?

Megoldás. A kezdeti sebesség vízszintes és függőleges összetevői

Az OA szakasz mozgása két egyszerű mozgásra bontható: egyenletes vízszintesen és egyenletesen lassú függőlegesen:

Az A pontban

Akkor És

Ha egy test egyidejűleg több mozgásban vesz részt, akkor mindegyikben a másiktól függetlenül vesz részt, ezért az AB szakasz mozgási idejét a lefelé mozgás ideje - t 2 határozza meg. A felfelé mozgás ideje megegyezik a lefelé mozgás idejével, ami azt jelenti

Egyenletes vízszintes mozgással egyenlő időn belül a test az út egyenlő szakaszain halad át, ezért

Repülési tartomány

Test emelési magassága

20. példa. A pont egyenesen mozog a síkon az x=4(t-2) 2 törvény szerint. Mekkora a pont kezdősebessége v 0 és gyorsulása a? Határozzuk meg a v t =5 pont pillanatnyi sebességét a mozgás ötödik másodpercének elején.

Megoldás.

1) Mert v=x’, akkor v 0 =(4∙(t-2) 2)'=(4∙(t 2 -4t+4))'=(4t 2 -16t+16)'=8t-16

t=0-nál v 0=-16 m/s.

2) Mert a= , akkor a=(8t-16)’=8 m/s.

3) t=4-nél, mert 4 mp telt el 5 s kezdete előtt.

v t =5 =8t-16=8∙4-16=32 m/s.

Válasz: A pont kezdeti sebessége v 0 = -16 m/s, a gyorsulás a = 8 m/s, a pont sebessége a mozgás ötödik másodpercének elején v t = 5 = 32 m/s.

21. példa. Egy anyagi pont mozgását a következő egyenletek írják le: a) s=αt 3 ; b) s=αt 2 +βt. Hasonlítsa össze az átlagos sebességet és a kezdeti és végsebesség számtani átlagát! v vö. a 0 - t időintervallumban. Itt α és β pozitív állandók.

Megoldás. Emlékezzünk vissza az átlagos és a pillanatnyi sebesség definíciójára:

A pillanatnyi sebesség kifejezéseit a mozgásegyenlet differenciálásával kapjuk.

Az átlagsebesség kifejezései a görbe vonalú koordináta változásának az időhöz viszonyított arányában találhatók:

A számtani átlagsebesség kifejezéseit kapjuk:

Válaszoljunk a probléma körülményeire vonatkozó kérdésre. Látható, hogy „a” esetben az átlagos és a számtani átlagsebesség nem esik egybe, „b” esetben viszont egybeesik.

22. példa. Egy anyagi pont egyenletesen mozog egy görbe pályán. A pálya melyik pontján van a gyorsulás maximuma?

Megoldás.Íves pályán haladva a gyorsulás érintőlegesből és normálból áll. A tangenciális gyorsulás a sebesség nagyságának (moduljának) változásának sebességét jellemzi. Ha a sebesség nagysága nem változik, a tangenciális gyorsulás nulla. A normál gyorsulás a pálya görbületi sugarától függ a n = v 2/R. A gyorsulás a legkisebb görbületi sugarú pontban a legnagyobb, azaz. a C pontban.

23. példa. Egy anyagi pont a törvény szerint mozog:

1) Határozza meg a kezdeti koordinátát, a kezdeti sebességet és a gyorsulást az állandó gyorsulású mozgástörvényhez képest! Írja fel a sebesség vetületének egyenletét!

Megoldás. Az állandó gyorsulással járó mozgástörvény alakja

Ha ezt az egyenletet összehasonlítjuk a problémafeltétel egyenletével, azt kapjuk

x 0 = -1 m,

v 0 x = 1 m/s,

a x = -0,25 m/s2.

Felmerül a kérdés: mit jelent a mínuszjel? Mikor negatív egy vektor vetülete? Csak abban az esetben, ha a vektor a koordináta tengelye ellen irányul.

Ábrázoljuk az ábrán a kezdeti koordináta-, sebesség- és gyorsulásvektorokat.

Írjuk fel az alakba a sebesség egyenletét

és behelyettesíti a kapott adatokat (kiindulási feltételeket).

2) Határozza meg a sebesség és a gyorsulás időfüggését a mennyiségek definícióival!

Megoldás. Alkalmazzuk a sebesség és a gyorsulás pillanatnyi értékeinek definícióit:

A megkülönböztetést végrehajtva azt kapjuk v x = 1-0,25t, a x = -0,25 m/s 2.

Látható, hogy a gyorsulás nem időfüggő.

3) Rajzolja meg v x (t) és a x (t) grafikonját. Jellemezze a mozgást a grafikon egyes szakaszaiban.

Megoldás. A sebesség időfüggősége lineáris, a grafikon egyenes.

t = 0 v x = 1 m/s-nál. t = 4-nél, ahol v x = 0.

A grafikonon jól látható, hogy az „a” szakaszban a sebesség vetülete pozitív, és értéke csökken, i.e. a pont lassan mozog az x tengely irányában. A „b” szakaszban a sebesség vetülete negatív, modulusa növekszik. A pont az x tengellyel ellentétes irányban gyorsítva mozog. Következésképpen a grafikonnak az abszcissza tengellyel való metszéspontjában elfordulás következik be, a mozgás iránya megváltozik.

4) Határozza meg a fordulópont koordinátáit és a kanyarodáshoz vezető utat!

Megoldás. Ismételten jegyezzük meg, hogy a fordulóponton a sebesség nulla. Erre az állapotra a mozgásegyenletekből a következőket kapjuk:

A második egyenletből azt kapjuk t pv = 4 s. (Úgy tűnik, ennek az értéknek a megszerzéséhez nem szükséges grafikont építeni és elemezni). Helyettesítsük be ezt az értéket az első egyenletbe: x felület = -1+4-4 2 /8 = 1 m. Ábrázoljuk a pont mozgását!

A kanyarodáshoz vezető út az ábrán látható módon megegyezik a koordináták változásával: s kanyar =x kanyar -x 0 =1-(-1)=2 m.

5) Melyik időpontban halad át egy pont az origón?

Megoldás. A mozgásegyenletbe x = 0-t kell feltenni. A 0=-1+t-t 2 /8 vagy t 2 -8t+8=0 másodfokú egyenletet kapjuk. Ennek az egyenletnek két gyökere van: . t 1 = 1,17 s, t 2 = 6,83 s. Valójában egy pont kétszer megy át a koordináták origóján: „oda” és „vissza” mozgáskor.

6) Keresse meg a pont által megtett utat a mozgás megkezdése után 5 másodpercen belül, és ez idő alatti elmozdulást, valamint az átlagos haladási sebességet ezen az útszakaszon.

Megoldás. Először is keressük meg azt a koordinátát, ahol a pont 5 másodperces mozgás után ért, és jelöljük meg az ábrán.

x(5)=-1+5-5 2 /8= 0,875 m.

Mivel ebben az állapotban a pont a kanyar után helyezkedik el, a megtett út már nem egyenlő a koordináta változásával (mozgás), hanem két tagból áll: a kanyar előtti útból

s 1 = x felület - x 0 = 1 - (-1) = 2 m

és a kanyar után

s 2 = x felület - x(5) = 1 - 0,875 = 0,125 m,

s = s 1 + s 2 = 2,125 m.

A pont elmozdulása az

s x = x(5) - x 0 = 0,875 - (-1) = 1,875 m

Az átlagos haladási sebességet a képlet számítja ki

A vizsgált probléma a mozgás egyik legegyszerűbb típusát írja le - a mozgást állandó gyorsulással. A mozgás természetének elemzésének ez a megközelítése azonban univerzális.

24. példa. Egydimenziós, állandó gyorsulású mozgásnál a részecske koordinátájának és sebességének az időtől való függését a következő összefüggések írják le:

Hozzon létre kapcsolatot egy részecske koordinátája és sebessége között.

Megoldás. A t időt kizárjuk ezekből az egyenletekből. Ehhez a helyettesítési módszert alkalmazzuk. A második egyenletből az időt fejezzük ki és cserélje be az első egyenletbe:

Ha a mozgás az origóból indul ( x 0 =0) nyugalmi állapotból ( v 0 x =0), akkor a kapott függés alakot ölt

jól ismert az iskolai fizika tanfolyamomról.

25. példa. Egy anyagi pont mozgását a következő egyenlet írja le: , ahol i és j az x és y tengely egységvektorai, α és β pedig pozitív állandók. Az idő kezdeti pillanatában a részecske az x 0 = y 0 = 0 pontban volt. Határozzuk meg az y(x) részecskepálya-egyenletet!

Megoldás. A feladat feltételét a mozgásleírás vektoros módszerével fogalmazzuk meg. Térjünk át a koordináta módszerre. Az egységvektorok együtthatói a sebességvektor vetületei, nevezetesen:

Először egy első osztályú feladat megoldásával kapjuk meg az x(t) és y(t) függőséget.

28. példa. Magas toronyból h nagy sebességgel dobott egy követ v 0 a vízszinteshez képest α szögben. Megtalálja:

1) mennyi ideig lesz mozgásban a kő;

2) milyen távolságra s a földre esik;

3) milyen sebességgel esik a földre;

4) milyen β szöget zár be a kő röppályája a horizonttal a zuhanás pontjában;

5) a kő normál és érintőleges gyorsulása ezen a ponton, valamint a pálya görbületi sugara;

6) a kő emelésének legnagyobb magassága.

A légellenállás figyelmen kívül hagyása.

Megoldás. Ezt a feladatot példaként használva bemutatjuk, hogyan állítható fel általánosított formában az adott algoritmus ebbe az osztályba tartozó bármely probléma megoldására.

1. A probléma egy anyagi pont (kő) mozgását veszi figyelembe a Föld gravitációs mezőjében. Ezért ez egy állandó g gravitációs gyorsulású, függőlegesen lefelé irányuló mozgás.

A vízszinteshez képest szögben bedobott test mozgása

Tekintsük a V 0 sebességgel dobott test mozgását, amelynek vektora a horizonttal α szöget zár be, az XOY síkban, a testet a dobás pillanatában a koordináták origójába helyezve, amint az ábra mutatja. az 1. ábrán.

Ellenállási erők hiányában a horizonthoz képest szögben bedobott test mozgása a gravitáció hatására a görbe vonalú mozgás speciális esetének tekinthető. Newton 2. törvényének alkalmazása

∑ F i
kapunk
mg = ma,
		a = g
Az a gyorsulásvektor vetületei az OX és az OU tengelyekre egyenlőek:
			= −g
ahol g = const van		a gravitáció gyorsulása,							ami mindig
függőlegesen lefelé irányítva		számérték g = 9,8 m/s2;						= −g		mert op-amp tengely be

Az 1. ábra felfelé néz, abban az esetben, ha az OY tengely lefelé irányul, akkor a vektor vetülete

2 a műveleti erősítő tengelyén pozitív lesz(a problémák feltételeit elolvasva, a tengelyek irányát maga válassza ki, ha ez a feltételek között nincs feltüntetve).

Az a gyorsulásvektor vetületeinek értékei az OX és az OU tengelyeken okot adnak arra, hogy

a következő kimenet:

∙ a vízszintessel szögben bedobott test egyidejűleg két mozgásban vesz részt - vízszintesen egyenletesen és mentén egyenletesen változtatható.

függőlegesek.
A test sebessége ebben az esetben
	V = Vx + Vy
A test sebessége az idő kezdeti pillanatában (a test dobásának pillanatában)
V 0 = V 0 x			V 0 y .
A kezdeti sebességvektor vetületei az OX és az OU tengelyekre egyenlők
		Vcosα
V 0 év		V 0 sin α

Egyenletesen változó mozgás esetén a sebesség és az elmozdulás időfüggőségét a következő egyenletek adják meg:

V 0 + at

S 0 + V 0 t +

és S 0 a test sebessége és elmozdulása a kezdeti időpillanatban,

és S t a test sebessége és elmozdulása t időpontban.

A (8) vektoregyenlet vetületei az OX és OU tengelyekre egyenlők

V 0 x

Axt,

V ty = V 0 y + a y t

Const

V 0 y - gt

A (9) vektoregyenlet vetületei az OX és az OU tengelyekre egyenlők

S ox + V ox t +

a y t 2

S 0 év

Voy t +

a (4) egyenlőségeket figyelembe véve megkapjuk

S 0 év

Voy t -

gt 2

ahol Sox és Soy van

test koordinátái

az idő kezdeti pillanatában,

és Stx és Sty -

a test koordinátái a t időpontban.

t mozgása során (a dobás pillanatától a ráesés pillanatáig

szint) a test felemelkedik a maximális hmax magasságra, leereszkedik onnan és elrepül a dobási ponttól L távolságra (repülési távolság) - lásd az 1. ábrát.

1) Testmozgási idő t megtalálható a Sy in testkoordináták értékeinek figyelembevételével

Szója = 0, Sty = 0,

Voy és (14) értékét behelyettesítve a (13) rendszer második egyenletébe, megkapjuk

2) Repülési távolság L megtalálható, figyelembe véve a test koordinátáit Sх in

kezdeti időpont és t időpont (lásd 1. ábra)

Soх = 0, Stх = L,

Vox és (17) értékét behelyettesítve a (13) rendszer első egyenletébe, megkapjuk

		L = V 0 cosα × t,
ahonnan (16) figyelembe véve azt kapjuk
L = Vcosα ×	2V sin α

3) Maximális emelési magasság h max érték alapján megtalálható

V testsebesség a test maximális emelési pontjában

V 0 x

Mert ezen a ponton V y

A (11) és (13) rendszerek második egyenletét használva,

a Voу értéke, valamint az a tény

hogy a test maximális emelésének pontján Sy = hmax azt kapjuk

0 = V 0 sin α - g × t alatt

gt sub2

V 0 sin α × t -

hmax

ahol tpod - emelkedési idő - a mozgás ideje a test maximális emelésének magasságáig.

Ezt a rendszert megoldva megkapjuk

t = alatt

V 0 sin α

sin 2 α

A (16) és (22) értékek összehasonlítása alapot ad a következtetésre

· mozgás ideje a maximális testemelés magasságáig (t alatt ) egyenlő a test leereszkedésének idejével (tп) erről a magasságról, és egyenlő a test teljes mozgásának idejének felével, a dobás pillanatától az azonos szintre zuhanás pillanatáig

t alatt	Tsp

A V 0 sebességgel dobott test mozgásának tanulmányozása, amelynek vektora a vízszinteshez képest α szöget zár be, az XOY síkban nagyon jól látható számítógépes modellen.

"Testek szabadesése" az "Open Physics" számítógépes modellek gyűjteményében

PHYSIKON cég. Ebben a modellben különböző kezdeti feltételeket állíthat be.

Például az általunk vizsgált esetet meg kell adni (a „Clear” parancs) a kezdeti h = 0 feltétellel, és kiválasztani a V0 és α értékeket. A "Start" parancs bemutatja a test mozgását, és képet ad a mozgás pályájáról és a test sebességvektorainak irányáról meghatározott időpillanatokban.

2. ábra. A "Testek szabadesése" című számítógépes modell párbeszédablakja a részben

"Mechanika"; egy test elmozdul az origótól és ugyanarra a szintre esik.

Ha a probléma feltétele eltér az általunk vizsgált esettől, akkor szükséges

a probléma megoldásához a tengelyek irányát választva helyezze el a testet a kezdeti pillanatban

idő, ábrázolja a test pályáját az esésig, így

a test koordinátáinak meghatározásával az idő kezdeti és végső pillanatában. Akkor

használja a (3), (5), (8) és (9) egyenleteket a megoldás alapjául és a fent tárgyalt

algoritmus a probléma megoldására.

Nézzünk speciális eseteket.

6 1. A testet nagy sebességgel dobták ki V 0 , amelynek vektora szögben van irányítvaα to

horizonton, h magasságból és a dobás pontjától L távolságra esett. y kezdőbetűre

Szója = h,

és a fennmaradó koordináták értékei ugyanúgy lesznek kiválasztva, mint mi.

3. ábra. A "Testek szabadesése" című számítógépes modell párbeszédablakja a részben

"Mechanika"; a test a h = 50m pontból elmozdul és nulla szintre esik.

2. Egy testet V 0 sebességgel vízszintesen dobtak h magasságból, és a dobás pontjától L távolságra esett. Az általunk vizsgált esethez képest az a különbség, hogy a test értékei S-t koordinálnak y a kezdeti pillanatban szintén a (25) egyenlet határozza meg,

és a fennmaradó koordináták értékei ugyanúgy lesznek kiválasztva, mint mi. De ebben az esetben a test kezdeti sebessége az OU tengelyre vetítve nullával egyenlő (mivel α = 0), azaz.

a kezdeti sebességvektor vetületei az OX és OU tengelyekre egyenlők

V 0 év

4. ábra. A "Testek szabadesése" című számítógépes modell párbeszédablakja a részben

"Mechanika"; egy vízszintesen eldobott test h = 50m pontból elmozdul és nulla szintre esik.

Tekintsük egy test mozgását a Föld gravitációs mezőjében, a légellenállást nem vesszük figyelembe. Legyen a kidobott test kezdeti sebessége a horizonttal $\alpha $ szöget bezárva (1. ábra). Egy testet dobunk $(y=h)_0$ magasságból; $x_0=0$.

Ekkor a kezdeti pillanatban a testnek vízszintes ($v_x$) és függőleges ($v_y$) sebességkomponensei vannak. A sebesség vetületei a koordinátatengelyekre $t=0$ esetén egyenlőek:

\[\left\( \begin(array)(c) v_(0x)=v_0(\cos \alpha ,\ ) \\ v_(0y)=v_0(\sin \alpha .\ ) \end(array) \ jobb.\bal(1\jobb).\]

A test gyorsulása megegyezik a szabadtüzelés gyorsulásával, és mindig lefelé irányul:

\[\overline(a)=\overline(g)\left(2\right).\]

Ez azt jelenti, hogy a gyorsulás vetülete az X tengelyen nulla, az Y tengelyen pedig egyenlő: $a_y=g.$

Mivel a gyorsulási komponens az X tengely mentén nulla, a test sebessége ebben az irányban állandó érték, és megegyezik a kezdeti sebesség X tengelyre vetítésével (lásd (1)). A test mozgása az X tengely mentén egyenletes.

Az 1. ábrán látható helyzetben a test az Y tengely mentén először felfelé, majd lefelé mozog. Ebben az esetben a test gyorsulása mindkét esetben megegyezik a $\overline(g) gyorsulással.$ A test ugyanannyi időt tölt felfelé haladva tetszőleges $(y=h)_0$ magasságból a maximumig. emelési magasság ($h$) $h$-ról $(y=h)_0$-ra esésként. Következésképpen a test emelkedésének csúcsához képest szimmetrikus pontok azonos magasságban helyezkednek el. Kiderült, hogy a test pályája szimmetrikus az emelés csúcsához képest - és ez egy parabola.

A vízszintessel szögben eldobott test mozgási sebessége a következő képlettel fejezhető ki:

\[\overline(v)\left(t\right)=(\overline(v))_0+\overline(g)t\ \left(3\right),\]

ahol $(\overline(v))_0$ a test sebessége a dobás pillanatában. A (3) képlet két független mozgás sebességének összeadásának eredményeként tekinthető olyan egyenesek mentén, amelyekben a test részt vesz.

A sebesség tengelyre vetítésének kifejezései a következők:

\[\left\( \begin(array)(c) v_x=v_0(\cos \alpha ,\ ) \\ v_y=v_0(\sin \alpha -gt\ ) \end(tömb) \left(4\right ).\jobb.\]

A test elmozdulásának egyenlete gravitációs térben történő mozgáskor:

\[\overline(s)\left(t\right)=(\overline(s))_0+(\overline(v))_0t+\frac(\overline(g)t^2)(2)\left(5) \jobb),\]

ahol $(\overline(s))_0$ a test elmozdulása az idő kezdeti pillanatában.

Az (5) egyenletet az X és Y koordinátatengelyekre vetítve kapjuk:

\[\left\( \begin(array)(c) x=v_0(\cos \left(\alpha \right)\cdot t,\ ) \\ y=(h_0+v)_0(\sin \left( \alpha \right)\cdot t-\frac(gt^2)(2)\ ) \end(array) \left(6\right).\right.\]

A felfelé haladó test kezdetben egyenletesen lassú mozgást végez az Y tengely mentén, majd miután a test feljut, az Y tengely mentén egyenletesen gyorsul.

Az anyagi pont pályáját a következő egyenlet adja meg:

A (7) egyenlet alakjából világosan látszik, hogy a mozgás pályája parabola.

A vízszintessel szögben eldobott test felemelkedésének és repülésének ideje

A test által a maximális emelési magasság elérésére fordított időt a (4) egyenletrendszerből kapjuk. . A pálya tetején a testnek csak egy vízszintes komponense van, $v_y=0.$ Az emelkedési idő ($t_p$) egyenlő:

A test teljes mozgási ideje (a repülési idő ($t_(pol)))$ a (6) rendszer második egyenletéből adódik, tudva, hogy amikor a test a Földre esik, $y=0$, akkor:

A horizonthoz képest szögben elhajított test repülési hatótávolsága és emelési magassága

A test vízszintes repülési tartományának ($s$) az általunk megadott feltételek melletti meghatározásához a ($t_(pol)$) (9) repülési időt be kell cserélni az egyenletrendszer $x$ koordinátaegyenletébe. (6). $h=0,$ esetén a repülési távolság egyenlő:

A (9) kifejezésből az következik, hogy adott dobási sebességnél a repülési hatótáv maximum $\alpha =\frac(\pi )(4)$.

A test maximális emelési magassága ($h_(max)$) a (6) rendszer második egyenletéből adódik, behelyettesítve az emelési időt ($t_p$) (8):

A (11) kifejezés azt mutatja, hogy a test maximális emelési magassága egyenesen arányos a dobási sebesség négyzetével, és a dobási szög növekedésével növekszik.

Példák a megoldásokkal kapcsolatos problémákra

1. példa

Gyakorlat. Hányszorosára változik a vízszintes irányban $h$ magasságból kidobott test repülési ideje, ha a test dobásának sebességét $n$-szeresére növeljük?

Megoldás. Keressünk egy képletet egy test repülési idejének kiszámítására, ha vízszintesen dobjuk (2. ábra).

A probléma megoldásának alapjául a test egyenletesen gyorsított gravitációs térben történő mozgására vonatkozó kifejezést használjuk:

\[\overline(s)=(\overline(s))_0+(\overline(v))_0t+\frac(\overline(g)t^2)(2)\left(1.1\right).\]

A 2. ábra segítségével felírjuk az (1.1) egyenlet vetületeit a koordináta tengelyekre:

\[\left\( \begin(array)(c) X:x=v_0t;; \\ Y:y=h_0-\frac(gt^2)(2) \end(array) \right.\left( 1.2\jobbra).\]

A testnek a földre zuhanásakor $y=0,$ ezt a tényt használjuk, és a repülési időt az (1.2) rendszer második egyenletéből fejezzük ki:

Amint látjuk, egy test repülési ideje nem függ a kezdeti sebességétől, ezért ha a kezdeti sebesség $n$-szorosára nő, a test repülési ideje nem változik.

Válasz. Nem fog változni.

2. példa

Gyakorlat. Hogyan változik a test repülési hatótávja az előző feladatban, ha a kezdeti sebességet $n$-szorosára növeljük?

Megoldás. A repülési távolság az a távolság, amelyet egy test a vízszintes tengely mentén megtesz. Ez azt jelenti, hogy szükségünk van az egyenletre:

az első példa (1.2) rendszeréből. Az (1.3) pontban található repülési időt $t,$ helyett behelyettesítve megkapjuk a repülési távolságot ($s_(pol)$):

A (2.2) képletből azt látjuk, hogy adott mozgási körülmények között a repülési távolság egyenesen arányos a test dobásának sebességével, ezért ahányszorosára növeljük a kezdeti sebességet, a test repülési hatótávja annyival nő. sokszor.

Válasz. A test repülési hatótávja $n$-szorosára nő.

Tekintsük a levezetett képletek alkalmazására példaként a horizonttal szögben eldobott test mozgását légellenállás hiányában. Mondjuk egy hegyen, tengerszint feletti magasságban egy ágyú őrzi a parti vizeket. A lövedéket a horizonthoz képest szögben lőjük ki kezdeti sebességgel egy pontból, amelynek helyzetét a sugárvektor határozza meg (2.16. ábra).

Rizs. 2.16. A vízszinteshez képest szögben bedobott test mozgása

Kiegészítés.

Anyagi pont mozgásegyenleteinek levezetése a gravitációs térben

Írjuk fel a mozgásegyenletet (Newton második törvényének egyenlete):

ez azt jelenti, hogy bármilyen tömegű testek - anyagi pontok - azonos kezdeti feltételek mellett azonos gravitációs térben ugyanúgy mozognak. Vetítsük a (2.7.2) egyenletet a derékszögű koordinátarendszer tengelyére. Vízszintes tengely Óábrán látható. 13 pontozott vonal, tengely OY húzzuk át a pontot RÓL RŐL függőlegesen felfelé, és a vízszintes tengelyre OZ, szintén áthaladva a ponton RÓL RŐL, irányítsuk a vektorra merőlegesen felénk. Kapunk:

A függőleges irány definíció szerint a vektor iránya, tehát a vízszintes tengelyekre vetületei ÖKÖRÉs OY egyenlők nullával. A második egyenlet figyelembe veszi, hogy a vektor lefelé és a tengely felé irányul OY- fel.

Rizs. 2.17. A vízszintessel szöget zárt test mozgása.

Adjunk hozzá kezdeti feltételeket a mozgásegyenletekhez, amelyek meghatározzák a test helyzetét és sebességét a kezdeti időpillanatban t 0, hagyjuk t0 = 0. Ezután az ábra szerint. 2.7.4

Ha valamely függvény deriváltja nulla, akkor a függvény állandó, a (2.7.3) első és harmadik egyenletből kapjuk:

A második (2.7.3) egyenletben a derivált egyenlő egy állandóval, ami azt jelenti, hogy a függvény lineárisan függ az argumentumától, azaz

(2.7.7) és (2.7.9) kombinálásával megkapjuk a végső kifejezéseket a koordinátatengelyekre vonatkozó sebességvetületek időbeli függésére:

A harmadik egyenlet (2.7.11) azt mutatja, hogy a test pályája lapos és teljes egészében a síkban fekszik XOY, a és a vektorok által meghatározott függőleges sík. Nyilvánvalóan az utolsó állítás általános: akárhogyan is választjuk meg a koordinátatengelyek irányait, a horizonttal szögben bedobott test pályája lapos, mindig a kezdeti sebességvektor által meghatározott síkban fekszik és a szabad esés gyorsulás vektor.

Ha a három (2.7.10) egyenletet megszorozzuk a , , és és tengelyek egységvektoraival, majd ugyanezt megtesszük a három (2.7.11) egyenlettel, akkor megkapjuk a részecskesebesség időfüggését. vektor és sugárvektora. Figyelembe véve a kezdeti feltételeket:

A (2.7.12) és (2.7.13) képleteket azonnal, közvetlenül a (2.7.2)-ből megkaphatjuk, ha figyelembe vesszük, hogy a gravitációs gyorsulás állandó vektor. Ha a gyorsulás - a sebességvektor deriváltja - állandó, akkor a sebességvektor lineárisan függ az időtől, a sugárvektor pedig, amelynek időderiváltja az időtől lineárisan függő sebességvektor, négyzetesen függ az időtől. Ezt a (2.7.12) és a (2.7.13) relációkba írjuk a (2.7.4) alakban a kezdeti feltételek szerint kiválasztott konstansokkal - konstans vektorokkal.

Konkrétan a (2.7.13)-ból világos, hogy a sugárvektor három olyan vektor összege, amelyek a szokásos szabályok szerint összeadódnak, ami jól látható az ábrán. 2.18.

Rizs. 2.18. Az r(t) sugárvektor ábrázolása tetszőleges t időpontban három vektor összegeként

Ezek a vektorok:

Itt a mozgások függetlenségének elve, amelyet a fizika más területein ún szuperpozíció elve(ráfedések). Általánosságban elmondható, hogy a szuperpozíció elve szerint több hatás eredő hatása az egyes hatások hatásainak összege külön-külön. Ez a mozgásegyenletek linearitásának következménye.

Videó 2.3. A vízszintes és függőleges mozgások függetlensége gravitációs térben történő mozgáskor.

Helyezzük az origót a dobási pontra. Most =0 , a tengelyek, mint korábban, el lesznek forgatva úgy, hogy a tengely 0x vízszintes volt, a tengely 0у- függőleges, és a kezdeti sebesség a síkban volt x0y(2.19. ábra).

Rizs. 2.19. A kezdősebesség vetületei koordinátatengelyekre

Vetítsünk a koordinátatengelyekre (lásd (2.7.11)):

Repülési útvonal. Ha az időt kizárjuk a kapott egyenletrendszerből t, akkor megkapjuk a pályaegyenletet:

Ez egy parabola egyenlete, amelynek ágai lefelé irányulnak.

Repülési hatótáv magasból való lövés esetén h . Abban a pillanatban, hogy a test leesik (a lövedék a tenger felszínén lévő célpontot találja el). A fegyver és a cél közötti vízszintes távolság egyenlő . helyettesítés ; a pályaegyenletbe a repülési távolság másodfokú egyenletét kapjuk:

A másodfokú egyenletnek két megoldása van (jelen esetben pozitív és negatív). Pozitív megoldásra van szükségünk. A feladatunk másodfokú egyenletének gyökerének standard kifejezése a következő alakra redukálható:

pontban érhető el, ha h = 0.

Maximális repülési távolság. Hegy magasról lőve ez már nem így van. Keressük meg azt a szöget, amelynél elérjük a maximális repülési távolságot. A repülési távolságnak a szögtől való függése meglehetősen összetett, és ahelyett, hogy megkülönböztetnénk a maximumot, a következőképpen járunk el. Képzeljük el, hogy növeljük a kezdőszöget. Először is, a repülési távolság növekszik (lásd a (2.7.15) képletet), eléri a maximális értéket, és ismét csökkenni kezd (függőlegesen felfelé lövés esetén nullára). Így minden repülési tartományban, kivéve a maximumot, két iránya van a kezdeti sebességnek.

Térjünk vissza a repülési távolság másodfokú relativitásegyenletéhez, és tekintsük a szög egyenletének. Tekintve, hogy

írjuk át a következő alakba:

Ismét egy másodfokú egyenletet kaptunk, ezúttal egy ismeretlen mennyiségre. Az egyenletnek két gyöke van, ami két olyan szögnek felel meg, amelyeknél a repülési távolság egyenlő . De amikor , mindkét gyökérnek egybe kell esnie. Ez azt jelenti, hogy a másodfokú egyenlet diszkriminánsa nullával egyenlő:

hol következik az eredmény?

Amikor ez az eredmény reprodukálja a (2.7.16) képletet

Általában a tengerszint feletti magasság sokkal kisebb, mint a repülési távolság a síkságon. Amikor a négyzetgyök közelíthető a Taylor-sor kiterjesztésének első tagjaival, és megkapjuk a közelítő kifejezést

vagyis a lőtáv megközelítőleg a fegyver magasságának magasságával nő.

Amikor l = lmax,És a = a max , amint már említettük, a másodfokú egyenlet diszkriminánsa nullával egyenlő, megoldása a következő:

Mivel az érintő kisebb, mint egy, az a szög, amelynél a maximális repülési távolság elérhető, kisebb.

Maximális emelési magasság a kezdőpont felett. Ez az érték a pálya felső pontjában a sebesség függőleges komponensének nullával egyenlő egyenlőségétől határozható meg.

Ebben az esetben tehát a sebesség vízszintes összetevője nem egyenlő nullával